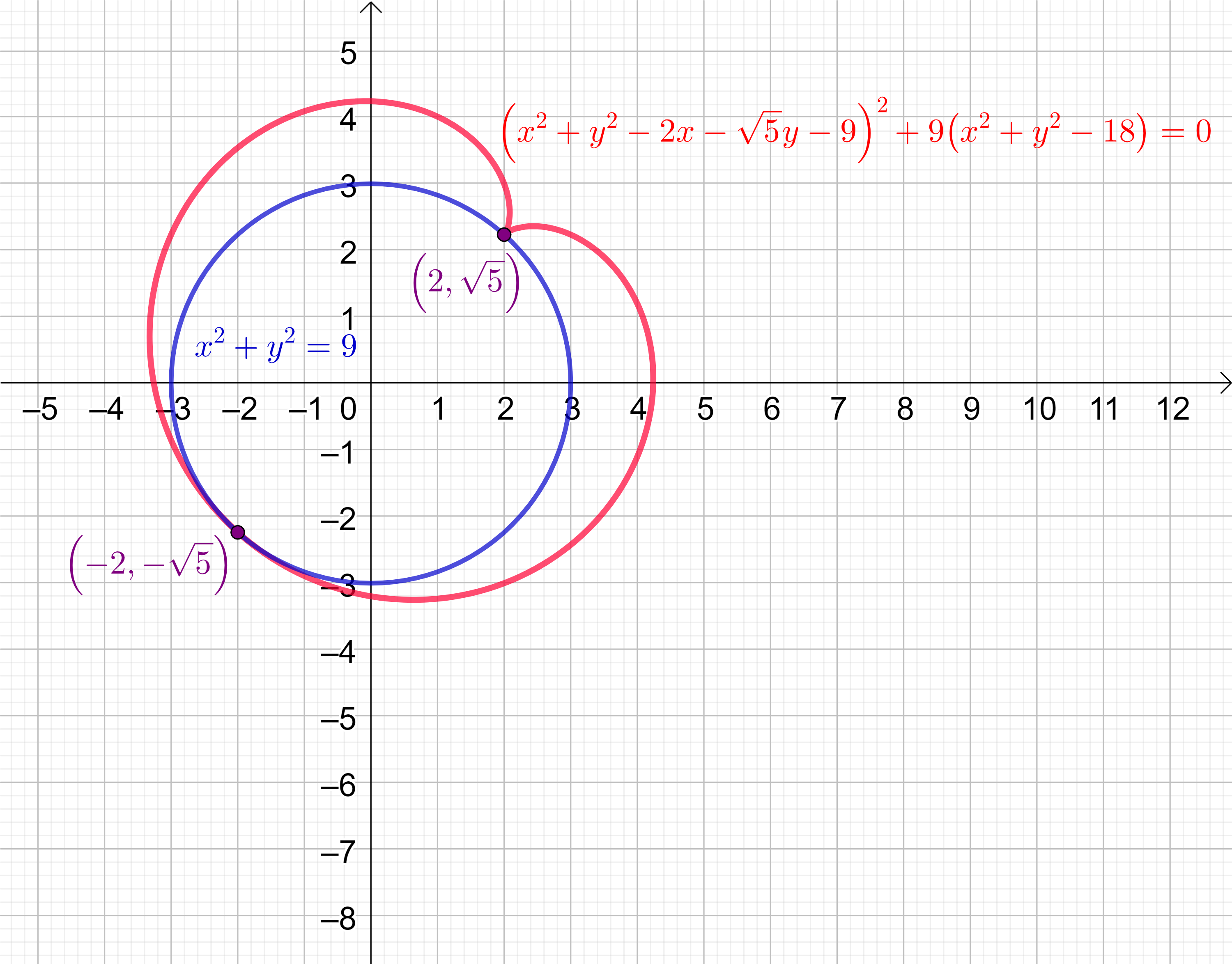Marija Briška
Sveučilišna prvostupnica, Fakultet za matematiku, Sveučilište u Rijeci,
e-mail: marijabriska24@gmail.com |
Milena Sošić
Docentica na Fakultetu za matematiku Sveučilišta u Rijeci,
e-mail: msosic@uniri.hr |
Sažetak
U ovom radu definira se i objašnjava pojam nožišne krivulje krivulje drugog reda obzirom na neku fiksnu točku ravnine koja može, ali ne mora pripadati krivulji drugog reda. Detaljno se argumentira izvod implicitne jednadžbe nožišne krivulje za pojedinu krivulju drugog reda obzirom na odabranu fiksnu točku ravnine i ukratko se obrazlažu osobitosti dobivene nožišne krivulje.
1Uvod
Krivulje drugog reda su algebarske krivulje u ravnini
\mathbb{R}^{2} određene općom jednadžbom
(1)
a_{11\,} x^{2} + 2a_{12\,} xy + a_{22\,} y^{2} + a_{1\,} x + a_{2\,} y + a_{0} = 0,
gdje su
a_{11}, a_{12}, a_{22}, a_{1}, a_{2}, a_{0}\in\mathbb{R} koeficijenti takvi da je
a_{11}^{2}+a_{12}^{2} +a_{22}^{2}\ne 0, čime se označava da je lijeva strana jednadžbe
(1) polinom drugog stupnja u varijablama
x,
y. Jednadžba
(1) je jednadžba skupa svih realnih nultočaka polinoma
F\colon \mathbb{R}^{2}\to\mathbb{R},
(2)
F(x,y)=a_{11\,} x^{2} + 2a_{12\,} xy + a_{22\,} y^{2} + a_{1\,} x + a_{2\,} y + a_{0}
drugog stupnja od dvije varijable
x i
y.
Krivulje drugog reda su parabola, kružnica, elipsa i hiperbola (vidi
[1]) koje se zajedničkim imenom nazivaju čunjosječnicama ili konikama jer se mogu dobiti presjekom kružne dvostruke stožaste plohe i ravnine, vidi
[4].
2Definicija nožišne krivulje
Neka
\mathcal{C} označava bilo koju krivulju drugog reda u ravnini i neka je
T=(x_{1},y_{1}) proizvoljna fiksna točka ravnine koja može, ali ne mora pripadati krivulji
\mathcal{C}. Nožišna krivulja, u oznaci
\mathcal{K}, krivulje
\mathcal{C} definira na sljedeći način.
|
|
Skup svih nožišta okomica spuštenih iz fiksne točke T=(x_{1},y_{1}) ravnine na tangente proizvoljno odabrane krivulje \mathcal{C} naziva se nožišnom krivuljom krivulje \mathcal{C}. |
Iz činjenice da u svakoj točki na krivulji
\mathcal{C} drugog reda postoji jednoznačna tangentu proizlazi da je za svaku krivulju drugog reda definirana nožišna krivulja obzirom na bilo koju točku ravnine. Općenito, iz navedene definicije proizlazi da je nožišna krivulja definirana za svaku proizvoljnu neprekidnu algebarsku ili transcendentnu krivulju
\Gamma u ravnini
\mathbb{R}^{2} i u
n-dimenzionalnom realnom prostoru
\mathbb{R}^{n} (
n\in\mathbb{N},
n\ge 2) za koju vrijedi da u svakoj točki na krivulji
\Gamma postoji jednoznačna tangenta, što je direktno povezano s pojmom diferencijabilnosti (ili derivabilnosti) funkcije i pojmom funkcije klase
C^{1} na njezinoj domeni, što se neće detaljnije obrazlagati u ovom radu, za više detalja vidi
[5, 6].
Iz definicije nožišne krivulje
\mathcal{K} krivulje
\mathcal{C} proizlazi da se pojedina točka na nožišnoj krivulji
\mathcal{K} krivulje
\mathcal{C} konstruira na sljedeći način.
|
1. |
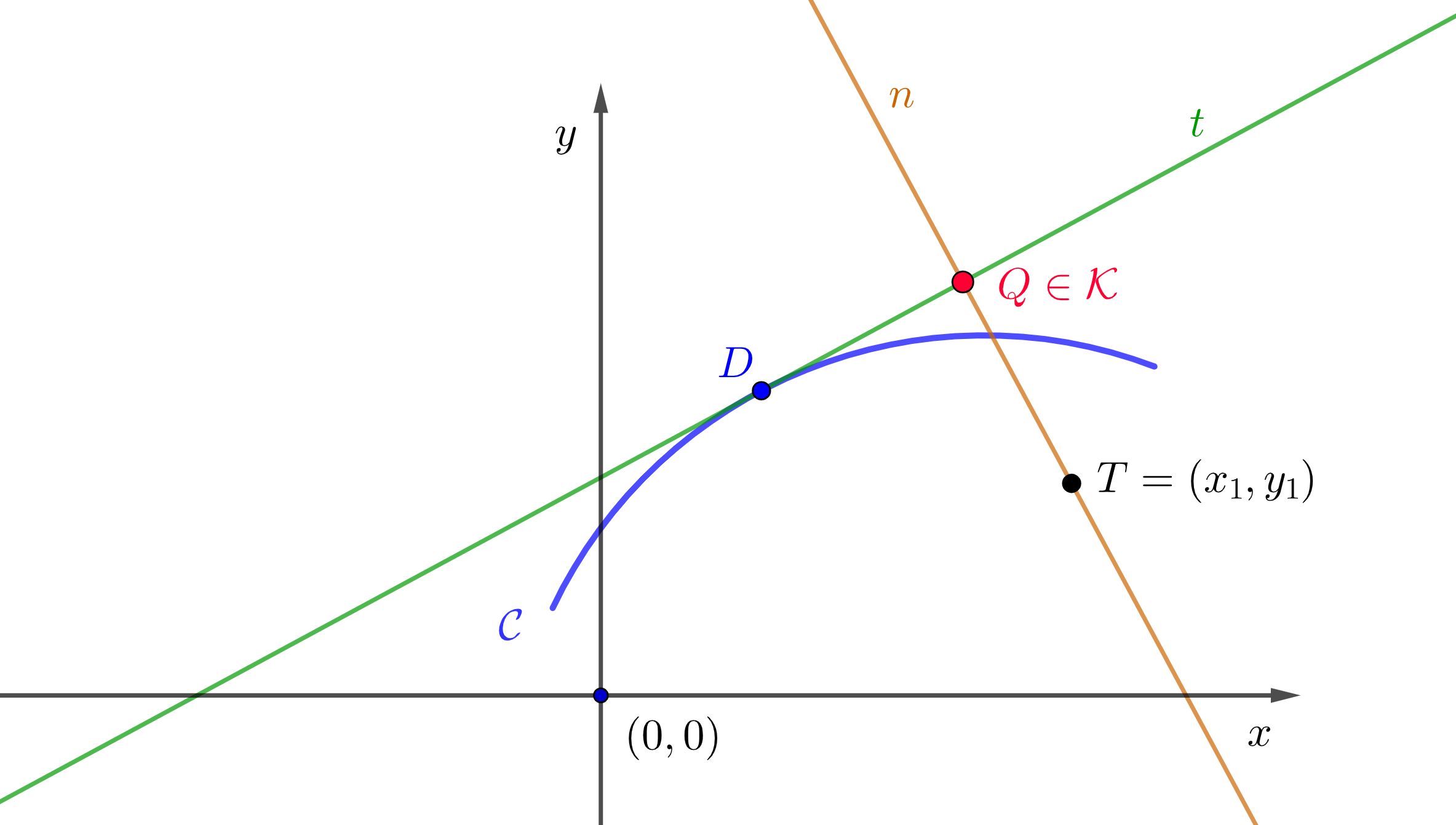
Odaberimo proizvoljnu krivulju \mathcal{C} i proizvoljnu fiksnu točku T=(x_{1},y_{1}) u ravnini obzirom na koju želimo odrediti nožišnu krivulju \mathcal{K} krivulje \mathcal{C}, pri čemu točka T može, ali ne mora pripadati odabranoj krivulji \mathcal{C}.
|
|
2. |
Nacrtajmo tangentu t u bilo kojoj točki D (diralištu) na krivulji \mathcal{C}.
|
|
3. |
Na tangenti t nacrtajmo onu normalu n koja prolazi fisknom točkom T=(x_{1},y_{1}).
|
|
4. |
Presjek normale n i tangente t je točka koja je ujedno nožište okomice spuštene iz fiksne točke T=(x_{1},y_{1}) na tangentu t krivulje \mathcal{C}. |
Na slici
1 prikazana je konstrukcija točke
Q na nožišnoj krivulji
\mathcal{K} krivulje
\mathcal{C} obzirom na fiksnu točku
T=(x_{1},y_{1}) ravnine koja ne pripada krivulji
\mathcal{C}. Dakle, svaka točka na nožišnoj krivulji
\mathcal{K} krivulje
\mathcal{C} je presjek tangente
t u točki odabranoj na krivulji
\mathcal{C} i normale
n spuštene iz fiksne točke ravnine na tangentu
t, stoga se nameće potreba za određivanje odgovarajućih jednadžbi tangente i normale.
Neka je krivulja
\mathcal{C} drugog reda određena implicitnom jednadžbom
F(x,y)=0
koja je ujedno jednadžba skupa svih realnih nultočaka polinoma
F:\mathbb{R}^{2}\to\mathbb{R} drugog stupnja od dvije varijable, vidi
(1) i
(2). U suglasnosti sa standardnim oznakama
F_{x}=\frac{\partial F}{\partial x} i
F_{y}=\frac{\partial F}{\partial y} za parcijalne derivacije funkcije
F po prvoj i drugoj varijabli uvodimo oznake
(3)
F_{\xi}=F_{x}(\xi,\eta), \quad F_{\eta}=F_{y}(\xi,\eta)
za parcijalne derivacije funkcije
F u proizvoljnoj točki
D=(\xi,\eta) na krivulji
\mathcal{C} drugog reda. Tada je
(4)
F_{\xi} \left(x-\xi\right) + F_{\eta} \left(y-\eta\right)=0
implicitna jednadžba tangente u proizvoljnoj točki (diralištu)
D=(\xi,\eta) na krivulji
\mathcal{C} drugog reda i analogno je
F_{\eta} \left(x-\xi\right) - F_{\xi} \left(y-\eta\right)=0
implicitna jednadžba normale u proizvoljnoj točki
D=(\xi,\eta) na krivulji
\mathcal{C} drugog reda. Označimo li sa
T=(x_{1},y_{1}) proizvoljnu fiksnu točku ravnine, tada je
(5)
F_{\eta} \left(x-x_{1}\right)-F_{\xi} \left(y-y_{1}\right)=0
implicitna jednadžba normale spuštene iz točke
T=(x_{1},y_{1}) na tangentu
(4) krivulje
\mathcal{C} drugog reda. Implicitna jednadžba nožišne krivulje
\mathcal{K} krivulje
\mathcal{C} drugog reda obzirom na proizvoljnu fiksnu točku
T=(x_{1},y_{1}) ravnine dobiva se eliminacijom
\xi i
\eta iz sustava dviju linearnih jednadžbi
(4) i
(5) i kvadratne jednadžbe
F(\xi,\eta)=0 s dvije nepoznanice
\xi i
\eta. Pritom treba imati na umu da se linearne jednadžbe
(4) i
(5) s dvije nepoznanice
x i
y zapravo razmatraju kao jednadžbe s dvije nepoznanice
\xi i
\eta koje su također linearne jer su parcijalne derivacije
F_{\xi} i
F_{\eta} funkcije
F u točki
D=(\xi,\eta) na krivulji drugog reda linearne. Sustav dviju linearnih jednadžbi
(4) i
(5) s dvije nepoznanice
\xi i
\eta ima jedinstveno rješenje
(\xi,\eta), gdje su
\xi i
\eta realne funkcije od dvije realne varijable
x i
y. Nadalje, iz svojstva da je rješenje
(\xi,\eta) razmatranog sustava dviju linearnih jednadžbi nultočka polinoma drugog stupnja od dvije varijable proizlazi da vrijedi
F(\xi,\eta)=0, čime se dobiva implicitna jednadžba u varijablama
x i
y koja je implicitna jednadžba nožišne krivulje krivulje drugog reda. Navedeni postupak raspisat ćemo detaljnije u nastavku prilikom određivanja implicitne jednadžbe nožišne krivulje za odabranu krivulju drugog reda obzirom na odabranu fiksnu točku ravnine.
Iz definicije nožišne krivulje proizlazi da nožišna krivulja
\mathcal{K} krivulje
\mathcal{C} drugog reda kao i njezina implicitna jednadžba ovisi o odabiru krivulje
\mathcal{C}, ali i proizvoljnoj fiksnoj točki ravnine (koja može, ali ne mora pripadati krivulji
\mathcal{C}) obzirom na koju se traži odgovarajuća nožišna krivulja krivulje
\mathcal{C}, vidi
[2]. Drugim riječima, u ovisnosti o različitom odabiru fiksne točke ravnine za neku fiksnu krivulju
\mathcal{C} dobiva se različita nožišna krivulja, što ćemo detaljnije argumentirati u poglavlju
3, gdje se objašnjava izvod implicitne jednadžbe nožišne krivulje parabole najprije obzirom na njezino tjeme, a zatim obzirom na njezino žarište (fokus) i naposljetku obzirom na točku na tjemenoj tangenti parabole, tj. tangenti parabole u njezinom tjemenu.
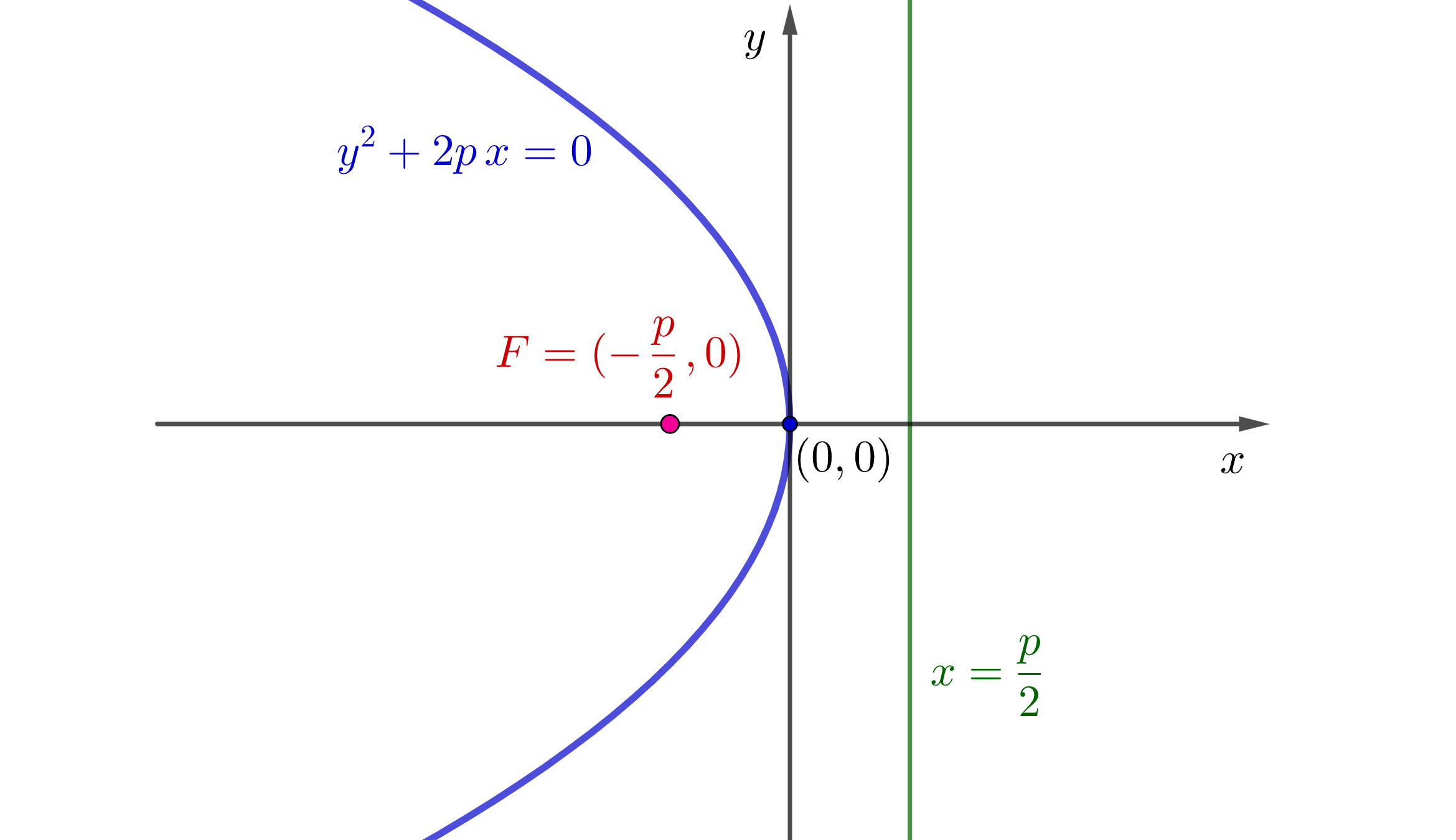
3Nožišna krivulja parabole y^{2}+2p\,x=0 obzirom na zadanu fiksnu točku
Parabola je krivulja u ravnini koja se definira kao skup svih točaka ravnine koje su jednako udaljene od zadane fiksne točke (žarišta ili fokusa) i zadanog fiksnog pravca (ravnalice ili direktrise) koji ne prolazi žarištem. Pravac koji prolazi žarištem, a okomit je na ravnalicu, naziva se os parabole. Os parabole siječe parabolu u tjemenu. Parabola je simetrična obzirom na svoju os. Udaljenost od žarišta do ravnalice naziva se žarišni parametar parabole. U nastavku razmatramo parabolu
\mathcal{P} u pravokutnom koordinatnom sustavu ravnine određenu implicitnom jednadžbom
(gdje je
p\in\mathbb{R}\backslash\lbrace 0\rbrace žarišni parametar parabole
\mathcal{P}) koja je ujedno jednadžba skupa svih realnih nultočaka polinoma
F:\mathbb{R}^{2}\to\mathbb{R},
drugog stupnja od dvije varijable
x i
y. Žarište parabole
\mathcal{P} je točka
F=(-\frac{p}{2},0), a ravnalica parabole
\mathcal{P} je pravac
x=\frac{p}{2} koji prolazi točkom
(\frac{p}{2},0) i paralelan je s ordinatom (
y-osi). Os parabole
\mathcal{P} je apscisa (
x-os), a tjeme parabole
\mathcal{P} je ishodište
O=(0,0) pravokutnog koordinatnog sustava ravnine. Parabola
\mathcal{P} je tjemenom okrenuta udesno i simetrična je obzirom na svoju os (
x-os), vidi sliku
2.
Jednadžba
(6) parabole
\mathcal{P} proizlazi iz jednadžbe
(1) ako je
a_{11}=a_{12}=0, a_{22}=1, a_{1}=2p, a_{2}=a_{0}=0. U suglasnosti s uvedenim oznakama
(3) proizlazi da su parcijalne derivacije funkcije
F u proizvoljnoj točki
D=(\xi, \eta) na paraboli
\mathcal{P} dane sa
(8)
F_{\xi} = 2p,\quad F_{\eta} = 2\eta,
gdje je
p\in\mathbb{R}\backslash\lbrace 0\rbrace, stoga primjenom
(8) i
(4) dobivamo da je implicitna jednadžba tangente u točki
D=(\xi,\eta) na paraboli
\mathcal{P} dana sa
2p\left(x-\xi\right)+2\eta\left(y-\eta\right)=0 koju nadalje zapisujemo u obliku
p\,x + \eta\,y - \left(\eta^{2} + p\,\xi\right) = 0, odnosno
(9)
p\,x +\eta\,y + p\,\xi = 0.
Pritom smo primijenili identitet
\eta^{2} = - 2p\,\xi koji direktno slijedi iz činjenice da je točka
D=(\xi,\eta) na paraboli
\mathcal{P} nultočka polinoma
(7).
U sljedeća tri odjeljka izvest ćemo jednadžbu nožišne krivulje parabole
\mathcal{P} određenu implicitnom jednadžbom
(6) najprije obzirom na njezino tjeme
O=(0,0), a potom obzirom na njezino žarište (fokus)
F=(-\frac{p}{2},0) i naposljetku obzirom na točku na tjemenoj tangenti parabole
\mathcal{P}.
3.1Nožišna krivulja parabole obzirom na njezino tjeme
Odredimo jednadžbu nožišne krivulje parabole
\mathcal{P} određene implicitnom jednadžbom
(6) obzirom na njezino tjeme
O=(0,0).
Uzimajući u obzir da je
(9) jednadžba tangente u točki
D=(\xi, \eta) odabranoj na paraboli
\mathcal{P}, odredimo jednadžbu normale spuštene iz tjemena parabole
\mathcal{P} na tangetu
(9) parabole
\mathcal{P}. Primjenom
(8) i
(5), pri čemu se tjeme
O=(0,0) parabole
\mathcal{P} razmatra kao fiksna točka ravnine iz koje se spuštaju normale na tangente parabole
\mathcal{P}, dobivamo da je
2\eta\,x - 2p\,y=0, odnosno
implicitna jednadžba normale
n spuštene iz tjemena parabole
\mathcal{P} na tangetu
(9) parabole
\mathcal{P}. Odredimo sada rješenje
(\xi,\eta) sustava
(11)
\left. \begin{array}{c} p\,\xi+y\,\eta = -p\,x \\ x\,\eta = p\,y \end{array} \right\rbrace
dviju linearnih jednadžbi
(9) i
(10) u kojima se
\xi i
\eta (koordinate točke
D=(\xi,\eta) na paraboli
\mathcal{P}) tretiraju kao nepoznanice, a
x,
y i
p\in\mathbb{R}\backslash\lbrace 0\rbrace kao koeficijenti. Primjenom metode supstitucije uz pretpostavku da je
x \ne 0 iz druge jednadžbe sustava
(11) proizlazi
\eta=\frac{p\,y}{x}, što uvrštavanjem u prvu jednadžbu sustava
(11) povlači da je
\xi=-\frac{x^{2}+y^{2}}{x}. Time je rješenje sustava
(11) oblika
(12)
(\xi,\eta)=\left(-\frac{x^{2}+y^{2}}{x}, \frac{py}{x}\right),
gdje je
x \ne 0 i
p \ne 0. Iz svojstva da je svaka točka na paraboli
\mathcal{P} određenoj implicitnom jednadžbom
(6) ujedno nultočka polinoma
(7) i pretpostavke da je
(\xi,\eta) točka na paraboli
\mathcal{P} proizlazi da je
F(\xi,\eta)=0, čime se dobiva da je
\frac{p^{2}y^{2}}{x^{2}} - 2p\,\frac{x^{2}+y^{2}}{x} = 0, odnosno
(13)
x\left(x^{2}+y^{2}\right) - \frac{p}{2}\,y^{2} =0
implicitna jednadžba nožišne krivulje parabole
\mathcal{P} obzirom na njezino tjeme, gdje je
p\ne 0.
Uspoređivanjem jednadžbe
(13) sa
y^{2}=\frac{x^{3}}{2a-x} eksplicitnom jednadžbom cisoide (vidi
[7]) čija je implicitna jednadžba
x\left(x^{2}+y^{2}\right) - 2a\,y^{2}=0 i čija je vertikalna asimptota pravac
x = 2a, zaključujemo da je nožišna krivulja parabole
\mathcal{P} obzirom na njezino tjeme zapravo cisoida čija je vertikalna asimptota pravac
x=\frac{p}{2}. S druge strane, iz činjenice da je pravac
x=\frac{p}{2} ravnalica parabole
\mathcal{P} proizlazi da je vertikalna asimptota cisoide ravnalica parabole
\mathcal{P}.
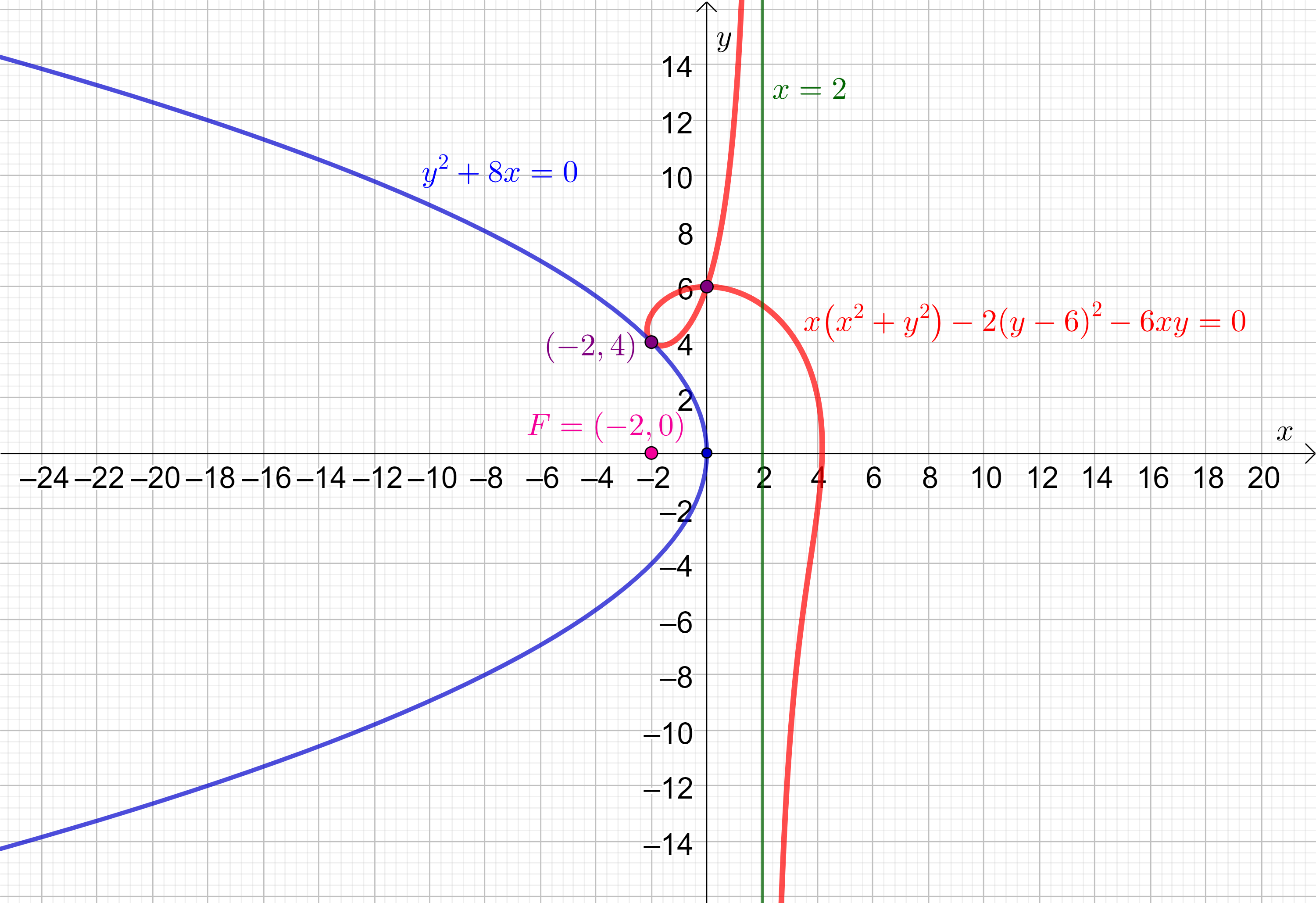
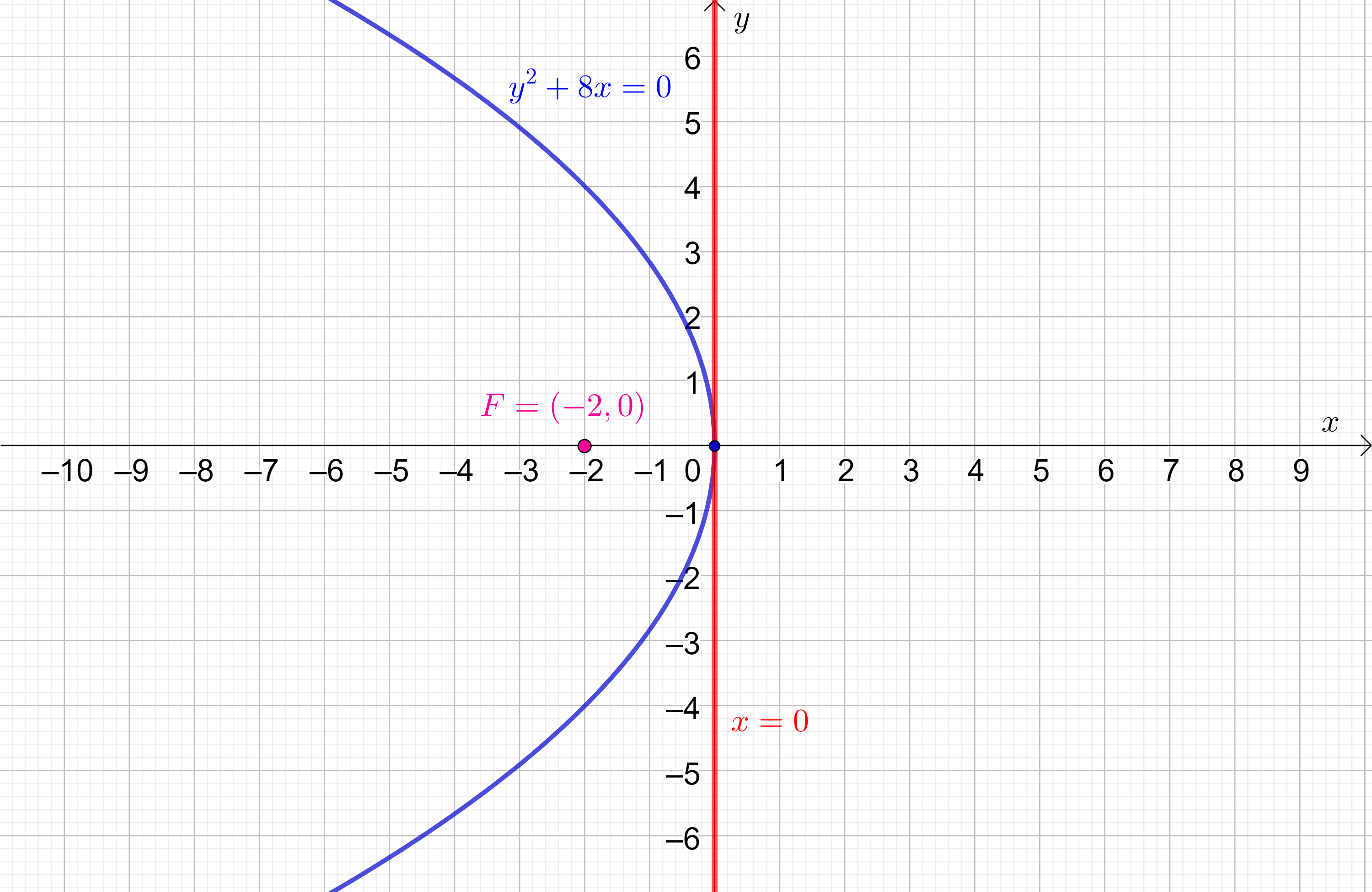
Na slici
3 prikazana je parabola
y^{2}+8x=0 (vidi
(6) za
p=4) i njezina nožišna krivulja obzirom na tjeme
O=(0,0) te parabole. Iz
(13) za
p=4 proizlazi da je nožišna krivulja određena jednadžbom
x\left(x^{2}+y^{2}\right) - 2y^{2}=0 i da je njezina vertikalna asimptota pravac
x=2, tj. ravnalica parabole. Promatrajući sliku
3 lako se može uočiti da cisoida, tj. nožišna krivulja parabole obzirom na njezino tjeme ima šiljak u tjemenu parabole, vidi
[3].
3.2Nožišna krivulja parabole obzirom na njezino žarište
Analogno kao u prethodnom odjeljku uz pretpostavku da je parabola
\mathcal{P} određena jednadžbom
(6) odredimo jednadžbu nožišne krivulje parabole
\mathcal{P} obzirom na njezino žarište
F=(-\frac{p}{2},0). Primjenom
(8) i
(5), gdje je žarište
F=(-\frac{p}{2},0) parabole
\mathcal{P} fiksna točka ravnine iz koje se spuštaju normale na tangente parabole
\mathcal{P}, dobivamo da je implicitna jednadžba normale spuštene iz žarišta
F=(-\frac{p}{2},0) parabole
\mathcal{P} na tangentu
(9) parabole
\mathcal{P} dana sa
2\eta\left(x+\frac{p}{2}\right)-2p\,y=0, odnosno
(14)
\eta\left(2x+p\right) - 2p\,y=0.
Promatrajmo sustav
(15)
\left. \begin{array}{c} p\,\xi+y\,\eta = -p\,x \\ \left(2x+p\right)\eta = 2p\,y \end{array} \right\rbrace
dviju linearnih jednadžbi
(9) i
(14) s dvije nepoznanice
\xi i
\eta. Primijetimo da iz definicije parabole direktno proizlazi da parabola ne siječe niti dira njezinu ravnalicu, što ima za posljedicu da u sustavu
(15) izraz
2x +p ne može biti jednak nuli, odnosno da je
x\ne -\frac{p}{2}. Naime, ako sustav
(15) razmatramo tako da
x i
y tretiramo kao nepoznanice, a
\xi i
\eta kao koordinate točke
D=(\xi,\eta) na paraboli
\mathcal{P}, onda se rješenje
(x,y) sustava
(15) geometrijski interpretira kao presjek tangente
(9) i normale
(14), čije koordinate
x i
y ovise o izboru točke
D=(\xi,\eta) na paraboli
\mathcal{P}, vidi sliku
1. Pretpostavimo li suprotno da je
2x +p=0, odnosno
x=-\frac{p}{2}, tada iz druge jednadžbe sustava
(15) slijedi da je
y=0, što je u suglasnosti s početnom pretpostavkom da svaka normala
(14) prolazi žarištem
F=(-\frac{p}{2},0) parabole
\mathcal{P}. Nadalje, pretpostavimo da je žarište
F=(-\frac{p}{2},0) parabole
\mathcal{P} rješenje sustava
(15). Tada iz prve jednadžbe sustava
(15) dobivamo da je
\xi=\frac{p}{2}, gdje je
\xi prva koordinata točke
D=(\xi,\eta) na paraboli
\mathcal{P}, što povlači da je uređen par
(\xi,\eta)=(\frac{p}{2},\eta) nultočka polinoma
(7), stoga mora vrijediti da je
\eta^{2}+p^{2}=0. Budući da je žarišni parametar
p parabole
\mathcal{P} bilo koji realan broj različit od nule, zaključujemo da jednadžba
\eta^{2}+p^{2}=0 nema realnih rješenja, što se geometrijski interpretira da točka
(\frac{p}{2},\eta) na ravnalici parabole
\mathcal{P} nije ujedno i točka na paraboli
\mathcal{P}. Drugim riječima, ravnalica parabole
\mathcal{P} i parabola
\mathcal{P} nemaju zajedničke točke.
Odredimo sada rješenje
(\xi,\eta) sustava
(15) dviju linearnih jednadžbi s dvije nepoznanice
\xi i
\eta. Koristeći prethodno obrazloženo da je
2x+p \ne 0 iz druge jednadžbe sustava
(15) proizlazi da je
\eta=\frac{2p\,y}{2x+p}, što uvrštavanjem u prvu jednadžbu sustava
(15) povlači da je
p\,\xi=-p\left(x + \frac{2y^{2}}{2x+p}\right), odakle dijeljenjem sa
p\in\mathbb{R}\backslash\lbrace 0\rbrace proizlazi
\xi=-\left(x + \frac{2y^{2}}{2x+p}\right). Rješenje sustava
(15) je uređen par
(\xi,\eta) = \left(-\left(x + \frac{2y^{2}}{2x+p}\right)\!, \frac{2p\,y}{2x+p}\right)
koji je ujedno nultočka polinoma
(7), stoga je
\begin{align*} \frac{4p^{2}\,y^{2}}{(2x+p)^{2}} - 2p\left(x + \frac{2y^{2}}{2x+p}\right) &=0 \\ 2p^{2}\,y^{2} - p\,x\left(2x+p \right)^{2}-4p\,xy^{2}-2p^{2}y^{2} &=0 \\ -p\,x\left(\left(2x+p \right)^{2} + 4y^{2}\right) &=0. \end{align*}
Dijeljenjem dobivene jednadžbe sa
-p\in\mathbb{R}\backslash\lbrace 0\rbrace proizlazi
x\left(\left(2x+p \right)^{2} + 4y^{2}\right)=0, odakle slijedi da je
ili
\left(2x+p \right)^{2} + 4y^{2}=0, što je u kontradikciji sa
\left(2x+p \right)^{2} + 4y^{2}\ne0 zbog
2x+p\ne0. Time je
(16) implicitna jednadžba nožišne krivulje parabole
\mathcal{P} obzirom na njezino žarište. Drugim riječima, nožišna krivulja parabole
\mathcal{P} obzirom na njezino žarište je
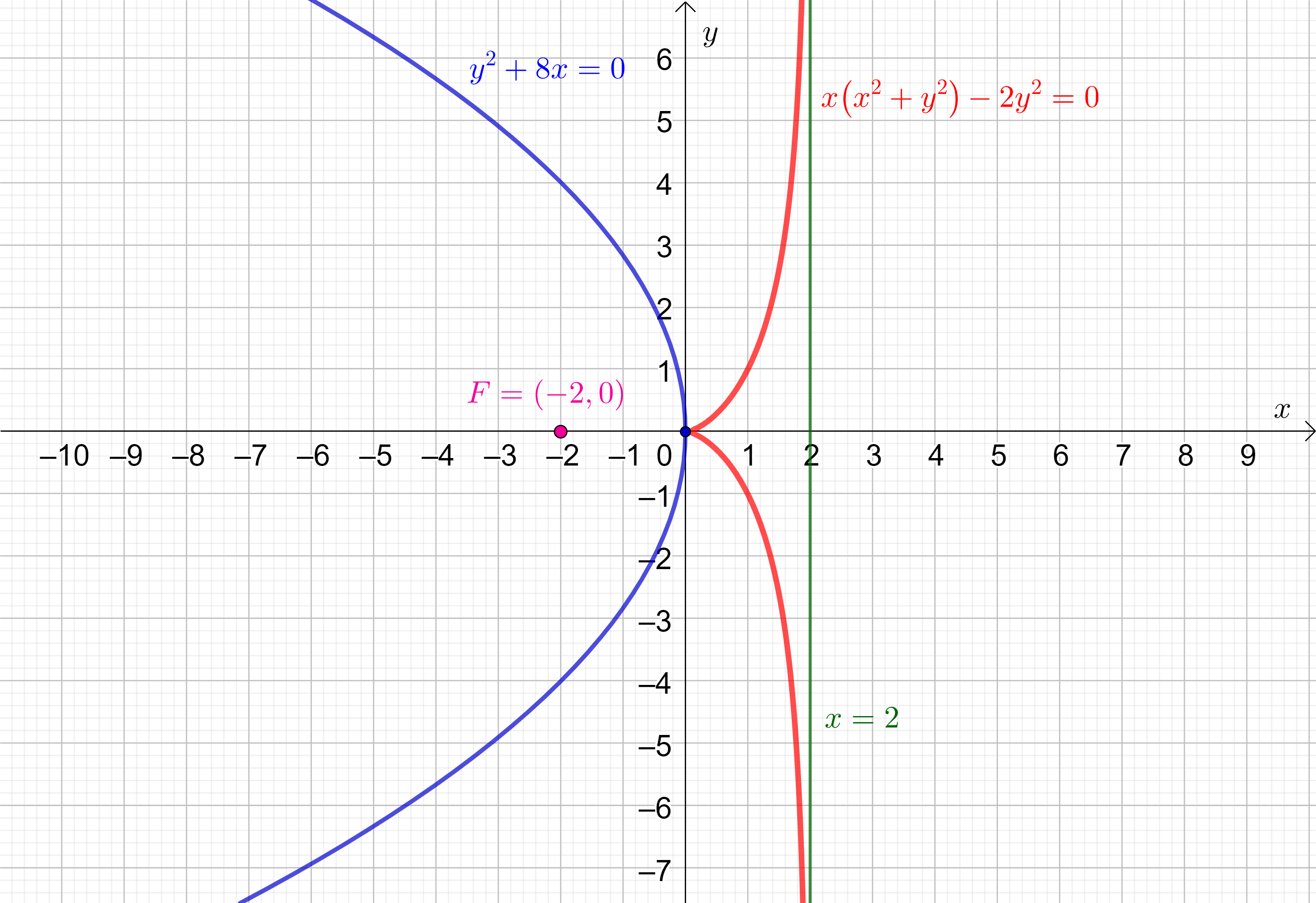
y-os, odnosno tjemena tangenta te parabole, vidi sliku
4, gdje je prikazana parabola
y^{2}+8x=0 i njezina nožišna krivulja (
y-os) obzirom na žarište
F=(-2,0) te parabole.
3.3Nožišna krivulja parabole obzirom na točku na tjemenoj tangenti parabole
Analogno kao u prethodna dva odjeljka uz pretpostavku da je parabola
\mathcal{P} određena jednadžbom
(6) odredimo jednadžbu nožišne krivulje parabole
\mathcal{P} obzirom na proizvoljnu fiksnu točku
S=(0,b),
b\in\mathbb{R} na tjemenoj tangenti parabole
\mathcal{P}. Primjenom
(8) i
(5), pri čemu se točka
S=(0,b) na tjemenoj tangenti parabole
\mathcal{P} razmatra kao fiksna točka ravnine iz koje se spuštaju normale na tangente parabole
\mathcal{P}, dobivamo da je implicitna jednadžba normale spuštene iz točke
S=(0,b),
b\in\mathbb{R} na tangentu
(9) parabole
\mathcal{P} dana sa
2\eta\,x-2p\left(y-b\right)=0, odnosno
Metodom supstitucije odredimo rješenje
(\xi,\eta) sustava
(18)
\left. \begin{array}{c} p\,\xi+y\,\eta = -p\,x \\ x\,\eta = p\left( y- b\right) \end{array} \right\rbrace
dviju linearnih jednadžbi
(9) i
(17) s dvije nepoznanice
\xi i
\eta. Pretpostavimo li da je
x \ne 0, tada iz druge jednadžbe sustava
(18) dobivamo da je
\eta=\frac{p\left( y- b\right)}{x}, što uvrštavanjem u prvu jednadžbu sustava
(18) povlači da je
p\,\xi=-p\,x-\frac{p\left( y^{2}- b\,y\right)}{x}, odnosno
p\,\xi=-p\,\frac{x^{2}+y^{2}-b\,y}{x}, odakle dijeljenjem sa
p\in\mathbb{R}\backslash\lbrace 0\rbrace proizlazi da je
\xi=-\frac{x^{2}+y^{2}-b\,y}{x}, stoga je rješenje sustava
(18) uređen par
(\xi,\eta) = \left(-\frac{x^{2}+y^{2}-b\,y}{x}, \frac{p\left(y-b\right)}{x}\right), \quad x \ne 0
koji je nultočka polinoma
(7), jer je
(\xi,\eta)\in\mathcal{P}, čime se dobiva implicitna jednadžba
\frac{p^{2}\left(y-b\right)^{2}}{x^{2}} - \frac{2p\left(x^{2}+y^{2}-b\,y\right)}{x} =0 iz koje množenjem s
\frac{x^{2}}{p} (gdje je
p\ne 0) proizlazi da je
p\left(y-b\right)^{2} -2x\left(x^{2}+y^{2}\right) +2b\,xy =0, odnosno
(19)
x\left(x^{2}+y^{2}\right) - \frac{p}{2}\left(y-b\right)^{2} - b\,xy =0
implicitna jednadžba nožišne krivulje parabole
\mathcal{P} obzirom na točku
S=(0,b),
b\in\mathbb{R} na tjemenoj tangenti parabole
\mathcal{P}, gdje je
p\ne 0. Krivulja određena jednadžbom
(19) za
b\ne 0 naziva se ofiurida, vidi
[7].
Napomenimo, ako je
b=0, onda je točka
S=(0,b) na tjemenoj tangenti parabole
\mathcal{P} tjeme parabole
\mathcal{P} i iz jednadžbe
(19) slijedi jednadžba
(13), što se geometrijski interpretira da se cisoida može razmatrati kao specijalan slučaj ofiuride. Međutim, treba naglasiti da su cisoida i ofiurida različite krivulje. Konkretno, cisoida ima šiljak, dok ofiurida ima dvostruku (čvornu) točku u kojoj presjeca samu sebe. Pokazuje se da je točka
S=(0,b), gdje je
b\in\mathbb{R}\backslash\lbrace 0\rbrace dvostruka točka ofiuride određene jednadžbom
(19) i da u točki
S postoje dvije tangente takve da je
k_{1}=0 koeficijent smjera jedne tangente
t_{1} i
k_{2}=\frac{2b}{p} koeficijent smjera druge tangente
t_{2}, za više detalja vidi
[3]. Primjenom poznate formule
y-y_{0}=k\left(x-x_{0}\right) za izračunavanje jednadžbe pravca koji prolazi točkom
(x_{0},y_{0}) i kojemu je poznat koeficijent smjera
k dobiva se da je u dvostrukoj točki
S=(0,b),
b\in\mathbb{R}\backslash\lbrace 0\rbrace ofiuride određene jednadžbom
(19) tangenta
t_{1} određena jednadžbom
y=b i da je tangenta
t_{2} određena jednadžbom
y = \frac{2b}{p}\,x + b, gdje je
p žarišni parametar parabole
\mathcal{P} različit od nule. Ofiurida određena jednadžbom
(19) kao i cisoida određena jednadžbom
(13) ima vertikalnu asimptotu
x=\frac{p}{2} koja je ujedno ravnalica parabole
\mathcal{P}. Realno rješenje sustava dviju jednadžbi
(19) i
(6) s dvije nepoznanice
x i
y je točka
(-\frac{p}{2},p) koja se geometrijski interpretira kao točka dodira ofiuride određene jednadžbom
(19) i parabole
\mathcal{P} određene jednadžbom
(6).
Na slici
5 prikazana je parabola
y^{2}+8x=0 i njezina nožišna krivulja (ofiurida) obzirom na točku
S=(0,6) na tjemenoj tangenti te parabole. Implicitna jednadžba te nožišne krivulje je
x\left(x^{2}+y^{2}\right)-2\left(y-6\right)^{2} - 6\,xy=0. Točka
S=(0,6) je dvostruka točka nožišne krivulje, stoga u točki
S=(0,6) postoje dvije tangente od kojih je jedna određena jednadžbom
y=6, a druga jednadžbom
y = 3x + 6. Vertikalna asimptota nožišne krivulje je pravac
x=2, odnosno ravnalica parabole
y^{2}+8x=0. Točka
(-2,4) je točka dodira parabole i njezine nožišne krivulje.
4Nožišna krivulja kružnice obzirom na njezinu fiksnu točku
Kružnica je zatvorena krivulja u ravnini koja se definira kao skup svih točaka ravnine jednako udaljenih od zadane fiksne točke koja se naziva središte kružnice. Udaljenost od središta kružnice do bilo koje točke kružnice naziva se polumjer kružnice i označava se sa
r, gdje je
r\gt 0. Dakle, kružnica je određena središtem i polumjerom. Kružnica sa središtem u točki
(x_{0},y_{0}) polumjera
r\gt 0 određena je jednadžbom
(x-x_{0})^{2} + (y-y_{0})^{2} = r^{2}, stoga je
jednadžba kružnice
\mathcal{K} sa središtem u ishodištu polumjera
r\gt 0. Odredimo implicitnu jednadžbu nožišne krivulje kružnice
\mathcal{K} obzirom na proizvoljnu fiksnu točku odabranoj na kružnici
\mathcal{K} čija je implicitna jednadžba
x^{2} + y^{2} - r^{2}=0 jednadžba skupa svih realnih nultočaka polinoma
F:\mathbb{R}^{2}\to\mathbb{R},
(21)
F(x,y)=x^{2} + y^{2} - r^{2}
drugog stupnja od dvije varijable
x i
y. Koristeći uvedene oznake
(3) u ovom slučaju su parcijalne derivacije funkcije
F u proizvoljnoj točki
D=(\xi,\eta) na kružnici
\mathcal{K} dane sa
(22)
F_{\xi} = 2\xi,\quad F_{\eta} = 2\eta.
Primjenom
(22) i
(4) dobivamo da je implicitna jednadžba tangente u točki
D=(\xi,\eta) na kružnici
\mathcal{K} dana sa
2\xi\left(x-\xi\right)+2\eta\left(y-\eta\right)=0, odnosno
\xi\,x + \eta\,y - \left(\xi^{2} + \eta^{2}\right) = 0 koju primjenom svojstva da je točka
D=(\xi,\eta) na kružnici
\mathcal{K} nultočka polinoma
(21) zapisujemo u obliku
(23)
\xi\,x + \eta\,y - r^{2} = 0.
Označimo li sa
(x_{1},y_{1}) proizvoljnu fiksnu točku na kružnici
\mathcal{K}, tada primjenom
(22) i
(5) dobivamo da je
2\eta\left(x-x_{1}\right)-2\xi\left(y-y_{1}\right)=0, odnosno
(24)
\eta\left(x-x_{1}\right)-\xi\left(y-y_{1}\right)=0
implicitna jednadžba normale spuštene iz točke
(x_{1},y_{1}) kružnice
\mathcal{K} na tangentu
(23) kružnice
\mathcal{K}. Odredimo rješenje
(\xi,\eta) sustava
(25)
\left. \begin{array}{c} x\,\xi+y\,\eta = r^{2} \\ -\left(y-y_{1}\right) \xi + \left(x-x_{1}\right) \eta = 0 \end{array} \right\rbrace
dviju linearnih jednadžbi
(23) i
(24) s dvije nepoznanice
\xi i
\eta (gdje su
x_{1} i
y_{1} koordinate fiksne točke
(x_{1},y_{1}) na kružnici
\mathcal{K}, tj. nultočke polinoma
(21)) primjenom Cramerovog pravila prema kojemu sustav
(25) ima jedinstveno rješenje
(\xi,\eta) =(\frac{D_{1}}{D}, \frac{D_{2}}{D}) ako je determinanta
D različita od nule. Determinante
D,
D_{1} i
D_{2} dane su sljedećim izrazima
D = \left| \begin{array}{cc} x & y \\ -\left(y-y_{1}\right) & \left(x-x_{1}\right) \end{array}\right| = x\left(x-x_{1}\right) + y\left(y-y_{1}\right),
D_{1} = \left| \begin{array}{cc} r^{2} & y \\ 0 & \left(x-x_{1}\right) \end{array}\right| = r^{2}\left(x-x_{1}\right), \qquad D_{2} = \left| \begin{array}{cc} x & r^{2} \\ -\left(y-y_{1}\right) & 0 \end{array}\right| = r^{2}\left(y-y_{1}\right).
Pretpostavimo da je
x\left(x-x_{1}\right) + y\left(y-y_{1}\right)\ne 0, čime se podrazumijeva da je
(x,y)\ne (0,0) ili
(x,y)\ne (0,y_{1}) ili
(x,y)\ne (x_{1},0) ili
(x,y)\ne (x_{1},y_{1}). Tada je jedinstveno rješenje sustava
(25) uređen par
(\xi,\eta) = \left(\frac{r^{2}\left(x-x_{1}\right)}{x\left(x-x_{1}\right) + y\left(y-y_{1}\right)}, \frac{r^{2}\left(y-y_{1}\right)}{x\left(x-x_{1}\right) + y\left(y-y_{1}\right)}\right)
koji je nultočka polinoma
(21), stoga se dobiva implicitna jednadžba
\frac{r^{4}\left(\left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}\right)}{\left(x\left(x-x_{1}\right) + y\left(y-y_{1}\right)\right)^{2}}-r^{2}=0. Kraćenjem jednadžbe sa
r^{2} (gdje je
r\gt 0) i množenjem s nazivnikom razlomka na lijevoj strani jednadžbe dobiva se jednadžba
r^{2}\left(\left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}\right) - \left(x\left(x-x_{1}\right) - y\left(y-y_{1}\right)\right)^{2} = 0
koju zapisujemo u obliku
r^{2}\left[\left(x^{2}+y^{2}\right)-2\left(x_{1}\,x+y_{1}\,y\right) + \underbrace{x_{1}^{2} + y_{1}^{2}}_{=r^{2}}\,\right] = \left[\left(x^{2} + y^{2}\right) -\left(x_{1}\,x+y_{1}\,y\right)\right]^{2}.
Množenjem na lijevoj strani jednadžbe sa
r^{2}, kvadriranjem na desnoj strani jednadžbe i dodatnim sređivanjem jednadžbe dobiva se
(26)
\left( x^{2}+y^{2} - x_{1}\,x - y_{1}\,y -r^{2}\right)^{2} + r^{2}\left(x^{2} + y^{2} -2r^{2}\right) = 0
implicitna jednadžba nožišne krivulje kružnice
\mathcal{K} obzirom na njezinu proizvoljnu fiksnu točku
(x_{1},y_{1})\in\mathcal{K}. Krivulja određena jednadžbom
(26) naziva se kardioida, vidi
[3, 7]. Kardioida određena jednadžbom
(26) ima šiljak u točki
(x_{1},y_{1}) na kružnici
\mathcal{K} i dira kružnicu
\mathcal{K} u točki
(-x_{1},-y_{1}). Točke
(x_{1},y_{1}) i
(-x_{1},-y_{1}) su realna rješenja sustava dviju jednadžbi
(26) i
(20) s dvije nepoznanice
x i
y i centralnosimetrične su s obzirom na središte simetrije u središtu kružnice
\mathcal{K}.
Na slici
6 prikazana je kružnica sa središtem u ishodištu polumjera
3 određena jednadžbom
x^{2}+y^{2}=9 i njezina nožišna krivulja (kardioida) obzirom na točku
(2,\sqrt{5}) na toj kružnici. Implicitna jednadžba nožišne krivulje je
\left( x^{2}+y^{2} - 2x - \sqrt{5}y -9\right)^{2} + 9\left(x^{2} + y^{2} -18\right) = 0. Točka
(2,\sqrt{5}) na kružnici je šiljak nožišne krivulje kružnice koji je centralnosimetričan točki
(-2,-\sqrt{5}) s obzirom na središte simetrije u središtu kružnice. Pritom je
(-2,-\sqrt{5}) točka dodira kružnice i njezine nožišne krivulje.
5Nožišna krivulja elipse obzirom na njezino središte
Elipsa je zatvorena krivulja u ravnini koja se definira kao skup svih točaka ravnine za koje je zbroj udaljenosti od dvije fiksne točke (žarišta) konstantan. Elipsa je centralno simetrična sa središtem simetrije u polovištu dužine s rubovima u žarištima i dvostruko osno simetrična s osima simetrije: (1) pravac koji prolazi kroz žarišta i (2) simetrala dužine s rubovima u žarištima. Osi simetrije nazivaje se glavne osi, a njihovo sjecište je polovište dužine s rubovima u žarištima koje se naziva središte elipse. Elipsa sa središtem u točki
(x_{0},y_{0}) određena je jednadžbom
(27)
\frac{(x-x_{0})^{2}}{a^{2}} + \frac{(y-y_{0})^{2}}{b^{2}} = 1,
gdje su
a\gt 0 i
b\gt 0 poluosi takve da jedna od njih leži na jednoj glavnoj osi, a druga na drugoj glavnoj osi, pri čemu je jedan rub od obiju poluosi u središtu elipse. Ako pretpostavimo da je
(x_{0},y_{0})=(0,0), onda iz
(27) proizlazi da je jednadžba elipse
\mathcal{E} sa središtem u ishodištu pravokutnog koordinatnog sustava ravnine određena jednadžbom
(28)
\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1.
U ovom slučaju su koordinatne osi ravnine ujedno glavne osi.
Odredimo implicitnu jednadžbu nožišne krivulje elipse
\mathcal{E} obzirom na njezino središte, gdje je elipsa
\mathcal{E} određena jednadžbom
(28). Analogno razmatranjima provedenim u prethodnim poglavljima, implicitna jednadžba
\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} -1=0 elipse
\mathcal{E} je jednadžba skupa svih realnih nultočaka polinoma
F:\mathbb{R}^{2}\to\mathbb{R},
(29)
F(x,y)=\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} - 1
drugog stupnja od dvije varijable
x i
y. Uzimajući u obzir da su parcijalne derivacije funkcije
F u proizvoljnoj točki
D=(\xi,\eta) odabranoj na elipsi
\mathcal{E} oblika
(30)
F_{\xi} = \frac{2\xi}{a^{2}},\quad F_{\eta} = \frac{2\eta}{b^{2}},
primjenom
(30) i
(4) dobivamo da je implicitna jednadžba tangente u točki
D=(\xi,\eta) na elipsi
\mathcal{E} dana sa
\frac{2\xi}{a^{2}}\left(x-\xi\right)+\frac{2\eta}{b^{2}}\left(y-\eta\right)=0 koju nakon sređivanja uz primjenu svojstva da je točka
D=(\xi,\eta) na elipsi
\mathcal{E} nultočka polinoma
(29) zapisujemo u obliku
(31)
\frac{\xi}{a^{2}}\,x + \frac{\eta}{b^{2}}\,y - 1 = 0
i primjenom
(30) i
(5) dobivamo da je
(32)
\frac{\eta}{b^{2}}\,x - \frac{\xi}{a^{2}}\,y=0
implicitna jednadžba normale spuštene iz središta elipse
\mathcal{E} na tangentu
(31) elipse
\mathcal{E}.
Koristeći Cramerovo pravilo dobiva se da sustav
(33)
\left. \begin{array}{c} \dfrac{x}{a^{2}}\,\xi + \dfrac{y}{b^{2}}\,\eta = 1 \\ \\ -\dfrac{y}{a^{2}}\,\xi + \dfrac{x}{b^{2}}\,\eta = 0 \end{array} \right\rbrace
dviju linearnih jednadžbi
(31) i
(32) s dvije nepoznanice
\xi i
\eta ima jedinstveno rješenje
(\xi,\eta) =(\frac{D_{1}}{D}, \frac{D_{2}}{D}) ako je
D\ne 0, gdje je
D = \left| \begin{array}{cc} \frac{x}{a^{2}} & \frac{y}{b^{2}} \\ -\frac{y}{a^{2}} & \frac{x}{b^{2}} \end{array}\right| = \dfrac{x^{2}+y^{2}}{a^{2}\,b^{2}}, \quad D_{1} = \left| \begin{array}{cc} 1 & \frac{y}{b^{2}} \\ 0 & \frac{x}{b^{2}} \end{array}\right| = \dfrac{x}{b^{2}}, \quad D_{2} = \left| \begin{array}{cc} \frac{x}{a^{2}} & 1 \\ -\frac{y}{a^{2}} & 0 \end{array}\right| = \dfrac{y}{a^{2}}.
Iz činjenice da nijedna tangenta elipse ne prolazi ishodištem, što direktno slijedi iz jednadžbe
(31) (gdje se za
(x,y)=(0,0) dolazi u kontradikciju
-1=0), proizlazi da je
\frac{x^{2}+y^{2}}{a^{2}\,b^{2}}\ne 0, što povlači da sustav
(33) ima jedinstveno rješenje
(\xi,\eta) = \left(\frac{a^{2}\,x}{x^{2}+y^{2}}, \frac{b^{2}\,y}{x^{2}+y^{2}}\right)
koje je nultočka polinoma
(29), čime se dobiva implicitna jednadžba
\frac{a^{2}\,x^{2} + b^{2}\,y^{2}}{\left(x^{2}+y^{2}\right)^{2}}-1=0 iz koje množenjem s
-\left(x^{2}+y^{2}\right)^{2} proizlazi da je
(34)
\left(x^{2}+y^{2}\right)^{2} - \left(a^{2}\,x^{2} + b^{2}\,y^{2}\right) =0
implicitna jednadžba nožišne krivulje
\mathcal{K_{\mathcal{E}}} elipse
\mathcal{E} obzirom na središte elipse
\mathcal{E}. Realna rješenja sustava dviju jednadžbi
(34) i
(28) s dvije nepoznanice
x i
y su točke
(-a,0),
(a,0),
(0,-b),
(0,b) koje su točke dodira elipse
\mathcal{E} i nožišne krivulje
\mathcal{K_{\mathcal{E}}} elipse
\mathcal{E}. Navedene točke dodira su ujedno sjecišta elipse
\mathcal{E} i koordinatnih osi. Iz svojstva centralne simetričnosti elipse sa središtem simetrije u središtu elipse proizlazi da su točke
(-a,0) i
(a,0) kao i točke
(0,-b),
(0,b) centralnosimetrične s obzirom na središte simetrije u središtu elipse.
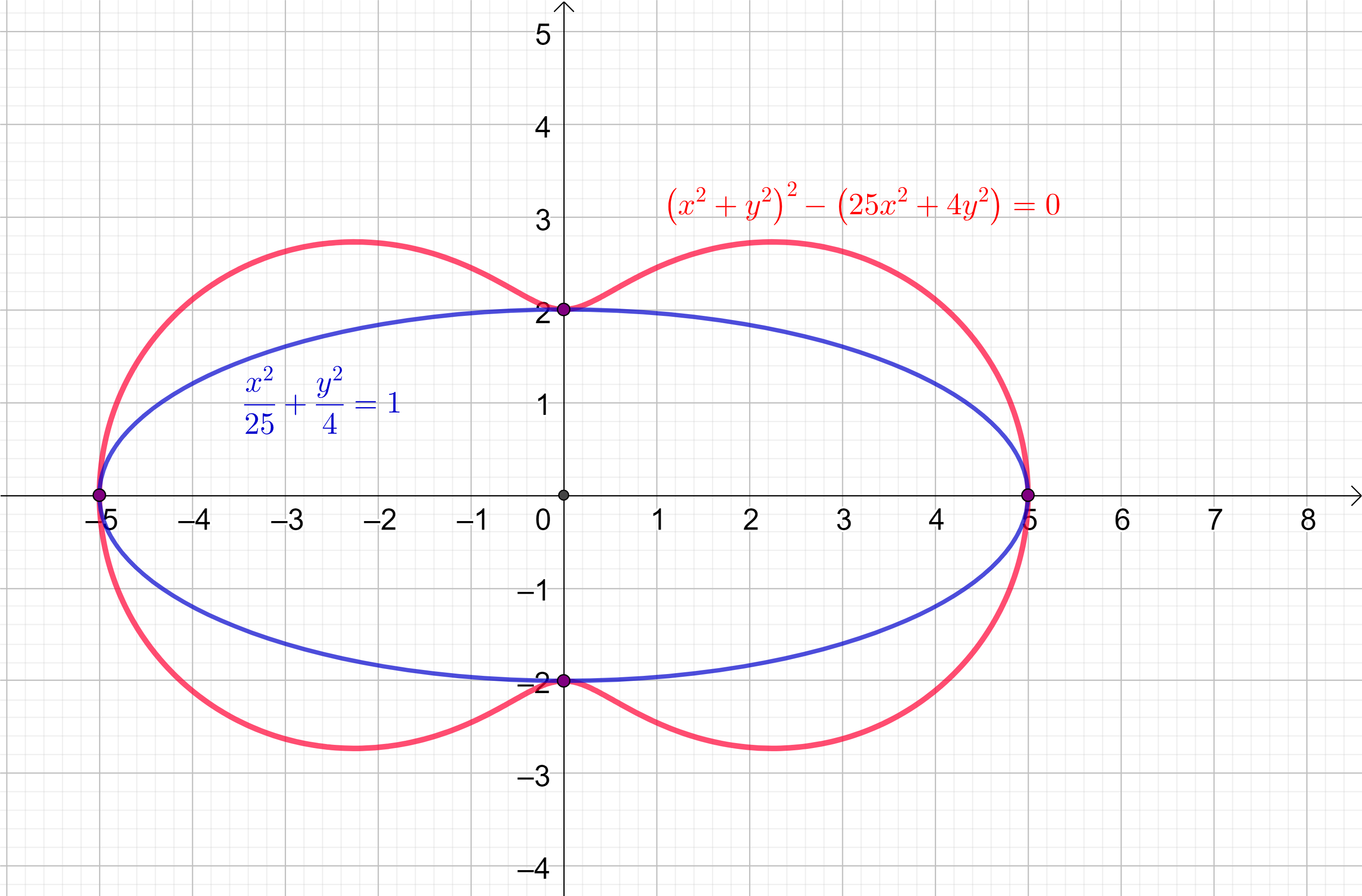
Na slici
7 prikazana je elipsa
\frac{x^{2}}{25}+\frac{y^{2}}{4}=1, njezina nožišna krivulja obzirom na središte te elipse i njihove točke dodira, gdje je nožišna krivulja određena implicitnom jednadžbom
\left(x^{2}+y^{2}\right)^{2} - \left(25\,x^{2} + 4\,y^{2}\right)=0.
6Nožišna krivulja hiperbole obzirom na njezino središte
Hiperbola je krivulja u ravnini koja se definira kao skup svih točaka ravnine za koje je apsolutna vrijednost razlike udaljenosti od dvije fiksne točke (žarišta) konstantna. Hiperbola se sastoji od dviju grana i ima dvije asimptote; centralno je simetrična sa središtem simetrije u polovištu dužine s rubovima u žarištima i dvostruko osno simetrična s osima simetrije: (1) realna os, tj. pravac koji prolazi kroz žarišta i (2) imaginarna os, tj. simetrala dužine s rubovima u žarištima. Polovište dužine s rubovima u žarištima naziva se središte hiperbole. Hiperbola sa središtem u točki
(x_{0},y_{0}) određena je jednadžbom
\frac{(x-x_{0})^{2}}{a^{2}} - \frac{(y-y_{0})^{2}}{b^{2}} = 1, stoga je jednadžba hiperbole
\mathcal{H} sa središtem u ishodištu pravokutnog koordinatnog sustava ravnine određena jednadžbom
(35)
\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1.
Odredimo implicitnu jednadžbu nožišne krivulje hiperbole
\mathcal{H} obzirom na njezino središte, gdje je hiperbola
\mathcal{H} određena jednadžbom
(35). Na sličan način kao u prethodnom poglavlju, implicitna jednadžba
\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} -1=0 hiperbole
\mathcal{H} je jednadžba skupa svih realnih nultočaka polinoma
F:\mathbb{R}^{2}\to\mathbb{R},
(36)
F(x,y)=\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} - 1
drugog stupnja od dvije varijable
x i
y. Uzimajući u obzir da su
(37)
F_{\xi} = \frac{2\xi}{a^{2}},\quad F_{\eta} = -\frac{2\eta}{b^{2}}
parcijalne derivacije funkcije
F u proizvoljnoj točki
D=(\xi,\eta) odabranoj na hiperboli
\mathcal{H}, primjenom
(37) i
(4) dobivamo da je
(38)
\frac{\xi}{a^{2}}\,x - \frac{\eta}{b^{2}}\,y - 1 = 0
implicitna jednadžba tangente u točki
D=(\xi,\eta) na hiperboli
\mathcal{H} i primjenom
(37) i
(5) dobivamo da je
(39)
\frac{\eta}{b^{2}}\,x + \frac{\xi}{a^{2}}\,y=0
implicitna jednadžba normale spuštene iz središta hiperbole
\mathcal{H} na tangentu
(38) hiperbole
\mathcal{H}. Nadalje, koristeći Cramerovo pravilo dobivamo da sustav
(40)
\left. \begin{array}{c} \dfrac{x}{a^{2}}\,\xi - \dfrac{y}{b^{2}}\,\eta = 1 \\ \\ \dfrac{y}{a^{2}}\,\xi + \dfrac{x}{b^{2}}\,\eta = 0 \end{array} \right\rbrace
dviju linearnih jednadžbi
(38) i
(39) s dvije nepoznanice
\xi i
\eta ima jedinstveno rješenje
(\xi,\eta) =(\frac{D_{1}}{D}, \frac{D_{2}}{D}), jer je
D = \left| \begin{array}{cc} \frac{x}{a^{2}} & -\frac{y}{b^{2}} \\ \frac{y}{a^{2}} & \frac{x}{b^{2}} \end{array}\right| = \dfrac{x^{2}+y^{2}}{a^{2}\,b^{2}}\ne 0, \quad D_{1} = \left| \begin{array}{cc} 1 & -\frac{y}{b^{2}} \\ 0 & \frac{x}{b^{2}} \end{array}\right| = \dfrac{x}{b^{2}}, \quad D_{2} = \left| \begin{array}{cc} \frac{x}{a^{2}} & 1 \\ \frac{y}{a^{2}} & 0 \end{array}\right| = -\dfrac{y}{a^{2}}.
Pritom
D\ne 0 direktno slijedi iz jednadžbe
(38), gdje se za
(x,y)=(0,0) dolazi u kontradikciju
-1=0, što se geometrijski interpretira da nijedna tangenta hiperbole ne prolazi ishodištem. Rješenje sustava
(40) je uređen par
(\xi,\eta) = \left(\frac{a^{2}\,x}{x^{2}+y^{2}}, -\frac{b^{2}\,y}{x^{2}+y^{2}}\right)
koji je nultočka polinoma
(36), čime se dobiva da je
(41)
\left(x^{2}+y^{2}\right)^{2} - \left( a^{2}\,x^{2} - b^{2}\,y^{2}\right) =0
implicitna jednadžba nožišne krivulje hiperbole
\mathcal{H} obzirom na njezino središte. Krivulja određena jednadžbom
(41) naziva se lemniskata, vidi
[3, 7]. Lemniskata određena jednadžbom
(41) ima dvostruku točku u središtu hiperbole i dira hiperbolu
\mathcal{H} u točkama
(-a,0) i
(a,0) koje su realna rješenja sustava dviju jednadžbi
(41) i
(35) s dvije nepoznanice
x i
y. Iz svojstva centralne simetričnosti hiperbole sa središtem simetrije u središtu hiperbole proizlazi da su točke
(-a,0) i
(a,0) centralnosimetrične s obzirom na središte simetrije u središtu hiperbole.
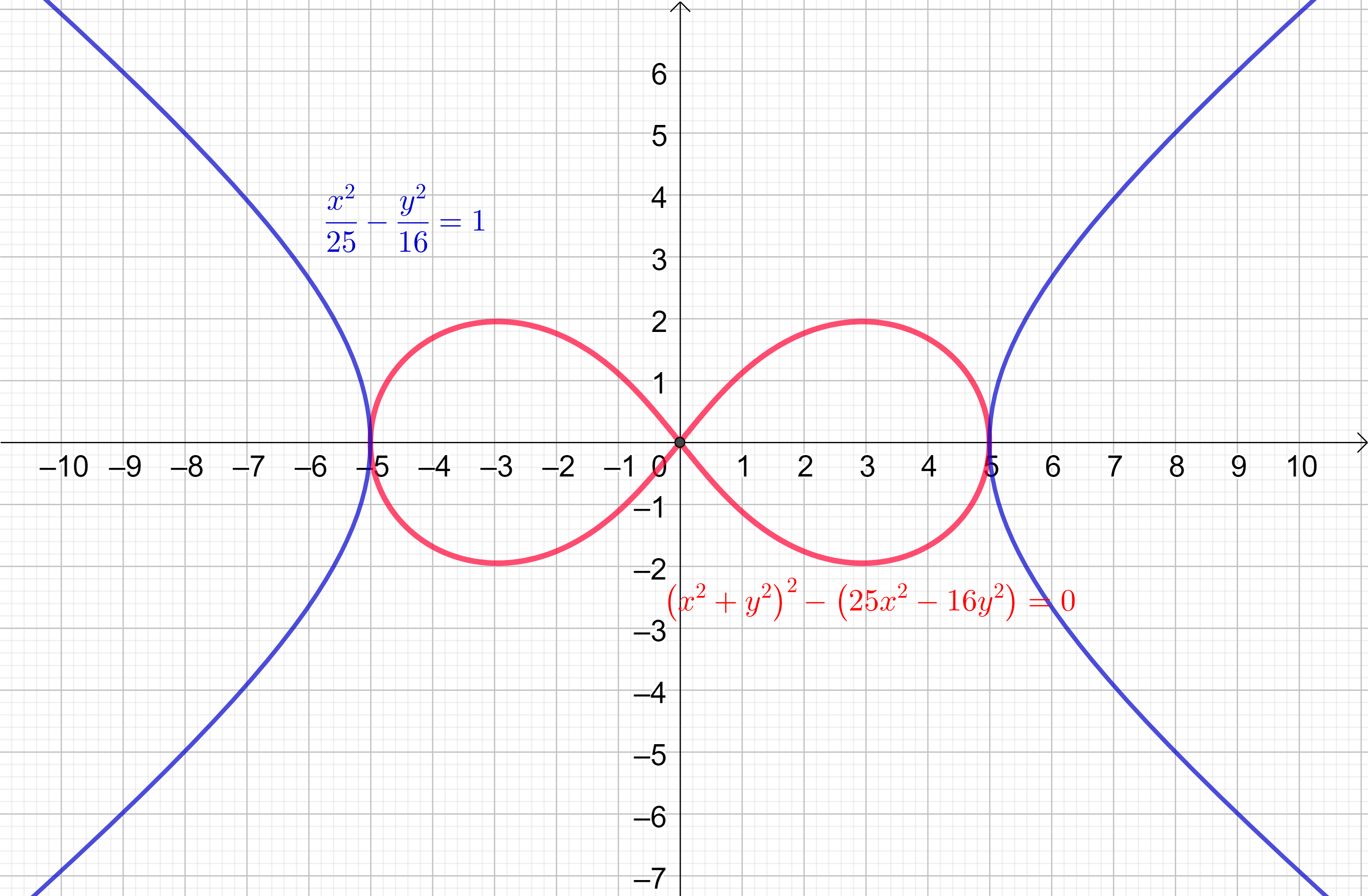
Na slici
8 prikazana je hiperbola
\frac{x^{2}}{25}-\frac{y^{2}}{16}=1, njezina nožišna krivulja obzirom na središte te hiperbole i njihove točke dodira
(-5,0) i
(5,0). Implicitna jednadžba te nožišne krivulje je
\left(x^{2}+y^{2}\right)^{2} - \left(25\,x^{2} - 16\,y^{2} \right)=0.
Literatura
|
[1] |
Apsen, B., Riješeni zadaci iz elementarne matematike, Tehnička knjiga, Zagreb, 1984. |
|
[2] |
Briška, M., Nožišne krivulje, završni rad, Fakultet za matematiku, Sveučilište u Rijeci, 2022. |
|
[3] |
Bronštejn, I. N. i suradnici, Matematički priručnik za inženjere i studente, Golden marketing - Tehnička knjiga, Zagreb, 2004. |
|
[4] |
Fenn, R., Geometry, Springer-Verlag, London, 2001. |
|
[5] |
Gray, A., Abbena, E., Salamon, S., Modern Differential Geometry of Curves and Surfaces with Mathematica, Boca Raton, CRS Press, 2006. |
|
[6] |
Kurepa, S., Matematička analiza, Funkcije više varijabli, Tehnička knjiga, Zagreb, 1984. |
|
[7] |
Savelov, A. A., Ravninske krivulje, Školska knjiga, Zagreb, 1979.
|