Pretpostavimo da metalni štap na jednom kraju zagrijavamo pomoću svijeće. Vrlo brzo moći ćemo primijetiti da se toplina širi, odnosno prenosi iz dijela štapa koji se nalazi točno iznad svijeće prema suprotnom kraju. No, kako taj proces nastaje, što je zapravo toplina, kako se razlikuje od pojma temperature i kako tu veličinu mjeriti? Toplina je fizikalna veličina kojom se opisuje energija koja prelazi s toplijeg tijela (tijelo s više toplinske energije) ka hladnijem (tijelo s manje toplinske energije), dok je temperatura fizikalna veličina koja opisuje sposobnost tijela da izmjenjuje toplinu s okolinom. Primjerice, zagrijemo li manju i veću prostoriju (manju/veću volumenom) istom količinom električne energije, manja će prostorija imati višu temperaturu od one veće, ali će toplina (količina toplinske energije) obje prostorije biti jednaka.

Postoji nekoliko načina prijenosa topline – provođenje ili kondukcija, strujanje ili konvekcija te zračenje ili radijacija. Prvi nastaje prilikom dodira tijela s izvorom topline, drugi strujanjem fluida, dok je treći posljedica elektromagnetskog zračenja (na primjer, na ovaj način Sunce grije Zemlju). Razvoj instrumenata pomoću kojih je bilo moguće vršiti pouzdana i ponovljena mjerenja te raditi usporedbu bilo je ključno za razvoj znanosti o toplini. Među takva otkrića i izume spada usavršavanje živinog termometra za mjerenje temperature i formiranje standardizirane ljestvice (Farenheit1, 1724.), otkriće latentne temperature i specifičnog toplinskog kapaciteta (Black2, 1760.) te njihovo mjerenje i razvoj prvog kalorimetra (Laplace3 i Lavoisier4, 1783.).

Ako se vratimo na polazni primjer, jedno od prirodnih pitanja je kako opisati prijenos topline matematički, odnosno temperaturu kao funkciju prostora i vremena, a to je problem koji spada u područje termodinamike. Ova se grana fizike razvila u 19. stoljeću, pri čemu se kao razlog navodi potreba za povećanjem učinkovitosti ranih parnih strojeva. Prvi je princip postavio francuski fizičar Sadi Carnot5 1824. godine; točnije, postavio je zakon koji se danas zove drugi zakon termodinamike. Prvi zakon termodinamike vezan je uz očuvanje energije i kaže da je promjena unutarnje energije sustava jednaka razlici topline dodane sustavu i rada koji sustav vrši. Drugim riječima, energija se ne može stvoriti ili uništiti, već se samo pretvara iz jednog oblika u drugi. Uz odsutstvo rada, promjena unutarnje energije tijela proporcionalna je promjeni temperature, ovisi o gustoći materijala te specifičnom toplinskom kapacitetu c.

Na početku 19. stoljeća, kada je ova grana još bila u fazi razvitka, francuski matematičar i fizičar Joseph Fourier6 predstavio je svoj rad “Sur la propagation de la chaleur” u kojem je opisao provođenje topline. Fourier je taj opis temeljio na zakonu koji u današnjoj notaciji glasi: te kaže da je brzina prijenosa toplinske energije po jedinici vremena te kroz područje jedinične površine proporcionalna temperaturnom gradijentu \nabla u, pri čemu K pozitivna konstanta i ovisi o materijalu od kojeg je tijelo napravljeno. Danas je ovaj zakon poznat kao Fourierov zakon provođenja topline. Rad je od iznimne važnosti zbog rješenja problema prijenosa topline, ali i zbog ideje koju je koristio pri rješavanju, a to je da se svaka periodična funkcija može prikazati pomoću reda oblika tj. korištenjem trigonometrijskih funkcija. Iako ova tvrdnja nije bila u potpunosti točna, ona ipak vrijedi za veliku i važnu klasu funkcija (te odgovor ovisi i o vrsti konvergencije), a rad na ovom pitanju potaknuo je veliki razvoj matematičke analize i drugih grana matematike. Fourierova analiza danas je izrazito važna zbog primjene u različitim područjima, a posebno obradi signala. Tvrdnje iz Fourierovog rada bile su potvrđene i eksperimentalno, no s obzirom da je rad nastao u vrijeme kada mnogi pojmovi matematičke analize vezani uz konvergenciju reda nisu bili precizno definirani ni proučavani, naišao je na kritike vodećih matematičara toga vremena, kao što su Lagrange7 i Laplace, te je trebalo još 15 godina da bude u potpunosti prihvaćen; rad pod nazivom “Théorie Analytique de la Chaleur” objavljen je 1822. godine.

U ovom članku razmatramo aspekt Fourierovog rada vezan uz problem provođenja topline te jednadžbu koja ga opisuje, međutim, nećemo se usredotočiti na njeno rješavanje već je cilj naglasiti njenu univerzalnost. Preciznije, pokazat ćemo da ova jednadžba ne opisuje samo prijenos topline već i procese i probleme iz drugih područja, kao što su kemija i financijska matematika. Ta je jednadžba poseban slučaj jednadžbe difuzije koja opisuje temeljno svojstvo ovog prirodnog fenomena, od fundamentalne je važnosti čak i u kvantnoj fizici te je igrala ulogu pri dokazu postojanja atoma (Perrin8, 1908.). članak je nastao na temelju završnog rada [8].


Središnji pojam ovog rada je parcijalna diferencijalna jednadžba koja opisuje prijenos topline. U ovoj cjelini navodimo osnovne pojmove i oznake, a kako bismo razumijevanje omogućili i čitateljima koji nisu upoznati s tim pojmovima, prisjetit ćemo se pojma derivacije te parcijalne derivacije. Derivacija funkcije f:I\to\mathbb{R} u točki c otvorenog intervala I=\langle a,b\rangle definira se kao ako taj limes postoji te se označava sa f'(c), odnosno \frac{df}{dx}(c). U tom slučaju kažemo da je f derivabilna (ili diferencijabilna) u točki c.
Nadalje, ako je f derivabilna u svakoj točki intervala I, kažemo da je derivabilna na intervalu I. Derivaciju drugog reda f'' (ako postoji), definiramo kao derivaciju funkcije x\mapsto f'(x). Analogno se definiraju derivacije višeg reda, te derivaciju m-tog reda označavamo s f^{(m)}.

Za funkcije više varijabli razlikujemo pojmove diferencijabilnosti i parcijalne derivacije; ako je funkcija diferencijabilna, onda postoje parcijalne derivacije, ali obrat općenito ne vrijedi. Za x=(x_{1},\ldots,x_{n})\in\mathbb{R}^{n} (n\in\mathbb{N}), neka je \Vert x\Vert :=\sqrt{x_{1}^{2}+\ldots x_{n}^{2}}. Otvorena kugla u \mathbb{R}^{n} sa središtem u x_{0}\in\mathbb{R}^{n} i radijusom r (r\gt 0) je skup Uočimo da K(x_{0},r) predstavlja skup svih točaka iz \mathbb{R}^{n} koje su od točke x_{0} udaljene za manje od r te da je otvorena kugla u \mathbb{R} zapravo otvoreni interval \langle x_{0}-r,x_{0}+r\rangle. Za skup \Omega\subseteq\mathbb{R}^{n} kažemo da je otvoren ako za svaki x\in \Omega postoji r\gt 0 takav da je K(x,r)\subseteq \Omega. Pojmove diferencijabilnosti i parcijalne derivacije u nastavku navodimo samo za n=2 (definicija je analogna za n\gt 2). Kažemo da je funkcija f:\Omega\to\mathbb{R}, gdje je \Omega\subseteq\mathbb{R}^{2} otvoren skup, diferencijabilna u točki (x_{0},y_{0})\in\Omega ako postoje A,B\in\mathbb{R} takvi da vrijedi te ako je diferencijabilna u svakoj točki iz \Omega, kažemo da je diferencijabilna na \Omega. Kažemo da funkcija f:\Omega\to\mathbb{R} u točki (x_{0},y_{0})\in\Omega ima parcijalnu derivaciju po varijabli x ako postoji limes Analogno definiramo parcijalnu derivaciju po varijabli y te koristimo oznake \frac{\partial f}{\partial x}, \partial_{x} f ili f_{x}, odnosno \frac{\partial f}{\partial y}, \partial_{y}f ili f_{y}. Parcijalnu derivaciju po varijabli x možemo interpretirati kao derivaciju funkcije x\mapsto f(x,y) za fiksni y, a po varijabli y kao derivaciju funkcije y\mapsto f(x,y) za fiksni x i u skladu s time možemo definirati parcijalne derivacije višeg reda. Parcijalne derivacije drugog reda označavat ćemo sa \frac{\partial^{2} f}{\partial x^{2}}, \frac{\partial^{2} f}{\partial x\partial y}, \frac{\partial^{2} f}{\partial y\partial x} i \frac{\partial^{2} f}{\partial y^{2}}, odnosno f_{xx}, f_{xy}, f_{yx} i f_{yy}. Tako, na primjer, za funkciju f(x,y)=x\sin y+x^{3}\cos y dobivamo a parcijalne derivacije drugog reda glase:
Za funkciju f:\Omega\to\mathbb{R}, gdje je \Omega\subseteq \mathbb{R}^{n} i x^{0}=(x_{1}^{0},\ldots,x_{n}^{0})\in\Omega, vektor parcijalnih derivacija (\partial_{x_{1}}f(x^{0}),\partial_{x_{2}}f(x^{0}),\ldots, \partial_{x_{n}}f(x^{0})) naziva se gradijent funkcijef u točki} x_{0} i označava s \nabla f(x^{0}).
Kako bismo opisali pojam parcijalne diferencijalne jednadžbe, opišimo ukratko osnovnu ideju diferencijalnih jednadžbi. Jednadžba primjer je obične diferencijalne jednadžbe, u kojoj tražimo sve funkcije f:\mathbb{R}\to\mathbb{R} za koje je (3) ispunjeno. Lako se vidi da svaka funkcija f:\mathbb{R}\to\mathbb{R}, f(x)=3x^{2}+C, gdje je C\in\mathbb{R}, zadovoljava jednadžbu (3) te da su funkcije zadane ovom familijom jedina rješenja. Uvrstimo li određeni realni broj umjesto općeg parametra C, dobivamo jedno partikularno rješenje.

Obična diferencijalna jednadžba m-tog reda je jednadžba oblika pri čemu je f funkcija jedne varijable x. Ako se umjesto funkcije jedne javlja funkcija više varijabli te njene parcijalne derivacije, onda govorimo o parcijalnoj diferencijalnoj jednadžbi.


U ovoj cjelini opisat ćemo izvod jednodimenzionalne jednadžbe provođenja topline kroz štap. Prijenos topline nastaje kao posljedica temperaturne razlike dvaju tijela; što je veća razlika, brži je prijenos. Uvodimo sljedeće oznake:

\bullet	m, V, \rho – masa, volumen i gustoća, respektivno
\bullet	c – specifični toplinski kapacitet
\bullet	K – koeficijent toplinske vodljivosti
\bullet	Q – količina topline
\bullet	u – temperatura

Prijenos energije vrši se iz područja više temperature u područje niže temperature u skladu sa sljedećim zakonima:

(1)	promjena vrijednosti topline u tijelu rezultira promjenom njegove temperature;
(2)	Fourierov zakon provođenja topline, koji u integralnom obliku možemo zapisati kao (prisjetimo se također i (1)): (5) \frac{\partial Q}{\partial t}=-K\oint_{S} \nabla u\cdot dS, gdje t predstavlja vrijeme, a S površinu kroz koju toplina protječe;
(3)	zakon očuvanja energije.

Specifični toplinski kapacitet c predstavlja količinu energije koja je potrebna da se temperatura dijela tijela jedinične mase uveća za jednu jedinicu. U tablici 1 prikazane su vrijednosti od c za neke materijale te vrijednosti koeficijenta toplinske vodljivosti K, spomenutog u uvodu.

Pretpostavimo da je promatrani štap neke duljine L te da su veličine \rho, c i K konstante, kao i površina poprečnog presjeka A. Pretpostavimo da su stranice tijela izolirane i samo rubovi mogu biti neizolirani te pretpostavimo da nema unutarnjeg izvora topline. Promatrani štap poistovjetit ćemo sa segmentom [0,L], a temperatura tijela opisana je funkcijom pri čemu varijabla x predstavlja poziciju, a t vrijeme. Iz Fourierovog zakona provođenja topline ((1), odnosno (5)) slijedi: Negativni predznak indicira da se toplina širi iz dijelova tijela s višom temperaturom u dijelove tijela s nižom temperaturom.

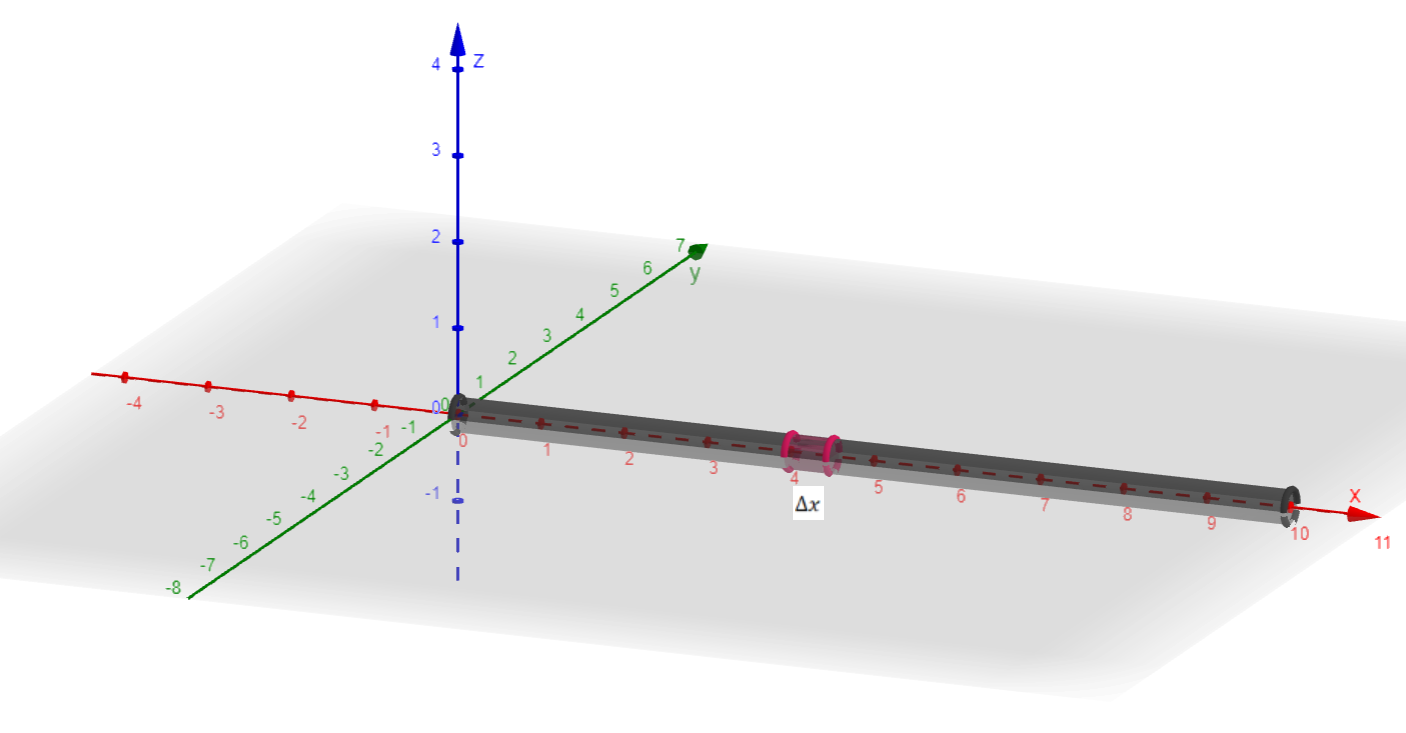
Izvedimo sada jednadžbu provođenja topline. Promotrimo podsegment [x,x+\Delta x] duljine \Delta x i pretpostavimo da je taj podsegment dovoljno male duljine da je njegova temperatura upravo u(x,t). Količina topline podsegmenta [x,x+\Delta x] proporcionalna je njegovoj masi (m=V\cdot\rho) i temperaturi, a ovisi i o materijalu (odnosno njegovom specifičnom toplinskom kapacitetu) te vrijedi: Prema zakonu očuvanja energije, jedino se preko krajnjih točaka može vršiti prijenos topline (jer su stranice izolirane) pa vrijedi da je promjena toplinske energije u [x, x+\Delta x] u vremenu \Delta t jednaka razlici toplinske energije koja je pridodana podsegmentu kroz lijevi rub i toplinske energije koja je oduzeta podsegmentu kroz desni rub te iz (6) slijedi: Podijelimo li gornji izraz sa c\rho A \cdot\Delta x\cdot\Delta t, dobivamo: Pustimo li sada da \Delta x,\Delta t \rightarrow 0, po definiciji parcijalne derivacije funkcije slijedi da je jednadžba provođenja topline dana s: gdje je \kappa = K/(c\cdot \rho). Konstanta \kappa je nenegativan broj i predstavlja toplinsku difuzivnost tijela (ova konstanta također ovisi o materijalu tijela te bolji vodiči imaju veći koeficijent) pa ga možemo označiti sa \alpha^{2} = \kappa.

Kako bismo pri rješavanju jednadžbe (7) dobili jedinstveno rješenje, potrebno je zadati:

1.	Početni uvjet, kojeg ćemo opisati funkcijom f:[0,L]\rightarrow\mathbb{R}. Funkcija f predstavlja početnu distribuciju temperature (tj. u trenutku t=0).
2.	Rubne uvjete, koji opisuju ponašanje temperature na rubovima danog tijela jer su rubovi neizolirani pa se na njima može događati gubitak toplinske energije.

Jedan dobro zadani problem provođenja topline glasi: gdje je (8) jednadžba provođenja topline (7) primijenjena na segment [0,L], (9) početna distribucija temperature 1-D tijela te su (10) rubni uvjeti. Fizikalno bismo interpretirali rubne uvjete (10) kao održavanje tih rubova na 0 stupnjeva. Fourier je dao rješenje ovog problema koje glasi: gdje su koeficijenti B_{n} dani sa: Postupak rješavanja problema zadanog s (8), (9) i (10) nipošto nije trivijalan, a kamoli početkom 19. stoljeća. Osim Fouriera, ideja prikaza funkcije pomoću trigonometrijskih bila je razmatrana i ranije. Jedan od matematičara koji je razmatrao takvo pitanje bio je Daniel Bernoulli9 koji je proučavao, na prvi pogled nepovezani, problem titranja žice (više o tom pitanju moguće je pročitati u [10]).

Prethodni primjer najjednostavniji je primjer problema ovog tipa, s obzirom da se prijenos topline vrši samo u jednom smjeru. Ako pri prijenosu ulogu imaju sve tri prostorne komponente, x, y i z, tada je temperatura funkcija jedne vremenske varijable t i prostorne varijable (x,y,z). Parcijalna diferencijalna jednadžba koja modelira provođenje topline glasi: gdje je \nabla^{2}u =\frac{\partial ^{2}u}{\partial x^{2}}+\frac{\partial^{2} u}{\partial y^{2}}+\frac{\partial^{2} u}{\partial z^{2}} Laplaceov operator (osim \nabla^{2}, koristi se i oznaka \Delta).


Godine 1827. škotski botaničar Robert Brown10 promatrajući mikroskopom čestice peluda suspendirane u vodi primijetio je da se one gibaju nasumično i vrlo nepravilno kreću u svim smjerovima. U to vrijeme je mislio da je pelud živi organizam pa bi to donekle objasnilo njegovo kretanje. Nakon Browna mnogi drugi znanstvenici replicirali su eksperiment te potvrdili Brownova zapažanja, i to ne samo s peludom u vodi već s bilo kojim dovoljno sitnim česticama suspendiranim u fluidu. Ovaj fenomen je nazvan Brownovim gibanjem11. Eksperimentalno je potvrđeno da su sitnije čestice u istom fluidu aktivnije od krupnijih te da su iste čestice manje aktivne u viskoznijem fluidu. Također, veća aktivnost čestica je postignuta dodavanjem topline u sustav.

Iako je eksperiment mnogo puta ponovljen i zapažanja su prihvaćena te su pronađena neka njegova svojstva, još uvijek nije bilo jasno odakle proizlazi to nasumično kretanje te postoji li fizikalni zakon pa time i matematički model koji ga opisuje. Godine 1905. Albert Einstein12 prvi opisuje, koristeći vjerojatnosni model, Brownovo gibanje. Einsteinovo objašnjenje je da ono proizlazi iz neprestanog sudaranja čestica fluida sa sitnim česticama koje su u njemu suspendirane. Do nasumičnog kretanja dolazi zbog neprestanog zadavanja udaraca suspendiranim česticama od strane molekula fluida sa svih strana te zbog tog neprestanog sudaranja suspendirane čestice imaju istu prosječnu kinetičku energiju kao i molekule fluida. Ova zapažanja bila su od nezanemarive važnosti pri dokazivanju postojanja atoma i određivanja njihove veličine, pošto u to vrijeme ideja da je sva materija sačinjena od atoma nije bila univerzalno prihvaćena.

Kako bismo uočili poveznicu između Brownovog gibanja i jednadžbe provođenja topline, opišimo Einsteinov argument iz 1905. godine. Pretpostavimo da promatramo K čestica suspendiranih u fluidu te da se u (proizvoljno kratkom) vremenskom intervalu Tx-koordinata proizvoljne čestice uveća za \varepsilon; naglašavamo da ovdje \varepsilon može biti i pozitivan i negativan realan broj, koji može biti različit za različite čestice (slika 6). U vremenskom intervalu T se broj čestica dK koje se pomaknu za neku udaljenost od \varepsilon do \varepsilon+d\varepsilon može izraziti kao: gdje je \varphi funkcija koja je različita od 0 samo za male vrijednosti od \varepsilon i koja ima sljedeća svojstva: i Uvjet (15) u kombinaciji s nenegativnošću od \varphi zapravo znači da je \varphi gustoća neke neprekidne slučajne varijable, a uvjet (16) da je \varphi parna funkcija. Uočimo da iz pretpostavke (16) odmah slijedi da je prisjetimo se, naime, da je podintegralna funkcija neparna, a integral neparne funkcije nad simetričnim segmentom jednak je 0. Neka sada funkcija (x,t)\mapsto f(x,t) pridružuje poziciji x i trenutku t broj čestica po jedinici volumena fluida na poziciji x u trenutku t tako da ukupan broj čestica uvijek bude očuvan, tj. da vrijedi: Definirajmo \alpha^{2} kao:
Sljedeći cilj je opisati distribuciju čestica nakon vremenskog intervala T. Uočimo da iz definicije funkcije \varphi slijedi Za mali T i \varepsilon, koristeći razvoj u Taylorov red, f(x,t+T) možemo aproksimirati s a f(x+\varepsilon,t) s Uvrštavanjem u (17) sada dobijemo Iz toga dobijemo jednadžbu: uočimo da je to zapravo jednadžba provođenja topline. Rješenje ovog problema za K promatranih čestica dano je sa: Uočimo da je za fiksni t, x\mapsto f(x,t) funkcija gustoće N(0,2\alpha^{2}t)-razdiobe pomnožena s K (slika 7). U nastavku ćemo na drugi način interpretirati zašto se ovdje pojavila ta razdioba.

Opišimo još ukratko poveznicu rješenja (19) i (11). Iako se radi o parcijalnoj diferencijalnoj jednadžbi istog tipa, drukčiji početni i rubni uvjeti imaju utjecaj na rješenja. Prisjetimo se da je s (11) opisano rješenje jednadžbe provođenja topline kroz štap duljine L te uz odgovarajuće početne i rubne uvjete, (9) i (10). Nadalje, B_{n} u (12) su zapravo Fourierovi koeficijenti proširenja funkcije iz (9) do neparne funkcije na [-L,L] (pritom se pretpostavlja da funkcija zadovoljava dodatna svojstva vezana uz konvergenciju pripadnog Fourierovog reda). U problemu iz ove cjeline f je funkcija varijable x i t, pri čemu je -\infty\lt x\lt \infty (za razliku od problema iz treće cjeline, gdje je 0\leqslant x\leqslant L) te problem odgovara problemu provođenja topline kroz štap beskonačne duljine, kojeg možemo identificirati s realnim pravcem. Taj problem modeliran je ponovno parcijalnom diferencijalnom jednadžbom \frac{\partial u}{\partial t}=\alpha^{2}\frac{\partial ^{2}u}{\partial x^{2}}, uz početni uvjet u(x,0)=g(x), -\infty\lt x\lt +\infty. Rješenje ovog problema (korištenjem svojstava Fourierove transformacije; detalje je moguće pogledati npr. u [12], 5.) dano je s gdje je H_{t}(x)=\frac{1}{\sqrt{4\pi t}}e^{-x^{2}/4\alpha^{2} t^{2}}, a * predstavlja operaciju konvolucije13, tj. Za Brownovo gibanje, početni uvjeti opisuju koncentraciju čestica u trenutku t=0, što nadalje možemo opisati pomoću distribucije \delta koja se naziva i Diracova delta “funkcija” te za koju vrijedi Sada iz (22) slijedi da je f(x,t)=\frac{K}{2\alpha\sqrt{\pi t}}e^{-\frac{x^{2}}{4\alpha^{2}t}}.




Pretpostavimo da je neka čestica podložna nezavisnim udarima u jednakim vremenskim intervalima, tj. u trenucima \tau,2\tau,3\tau itd., tako da se uslijed svakog udara može pomaknuti udesno (pozitivni smjer) za udaljenost h\gt 0 s vjerojatnošću p ili ulijevo (negativni smjer) za udaljenost h s vjerojatnošću q=1-p. Ovakvo gibanje možemo intepretirati kao gibanje na pravcu i pomak u vremenskom trenutku n\tau (za neki n\in\mathbb{N}) predstaviti kao realizaciju slučajne varijable koja ima distribuciju kao X, gdje je Za niz nezavisnih slučajnih varijabli (X_{n}) s prethodno opisanom distribucijom, slučajni proces (S_{n}) gdje je slučajna varijabla S_{n} definirana s naziva se jednostavna slučajna šetnja (simetrična ako je p=q). Jednu realizaciju takvog procesa možemo vidjeti na slici 8 (na x-osi se nalaze vremenski trenuci k\tau, k=1\ldots, n , a na y osi realizacija od S_{n}, pri čemu je h=1, \tau=1 i n=10). Na slici 10 također su prikazane trajektorije slučajne šetnje, ali ovaj put za veći n (n=1000).

Neka f(x,t) označava vjerojatnost da je čestica, krenuvši iz točke x=0 u trenutku t=0, nakon N udara (tj. u trenutku t=N\tau) postigla poziciju x. Kako se u točki x u trenutku t+\tau čestica može naći jedino ako je u prethodnom trenutku t bila u točki x-h ili točki x+h, vrijedi: Uočimo da je opisani proces sličan procesu nasumičnog sudaranja čestica u Brownovom gibanju. To donekle potkrijepljuje i slika 11 koja predstavlja simulacije slučajne šetnje u dvije dimenzije, pri čemu se čini da odabirom sve većeg n, gibanje sve više nalikuje kaotičnom gibanju koje je pod mikroskopom opazio Brown.

Fokusirajmo se sada na simetričnu šetnju u tri dimenzije. Neka je P čestica na poziciji točke r=(x_{1},x_{2},x_{3}) prostora \mathbb{R}^{3}. Nadalje, neka je p=1/6 vjerojatnost da se čestica P u bilo kojem trenutku k\tau\geq 0, k\in\mathbb{N}, pomakne na poziciju jedne od svojih šest najbližih susjednih točaka: (x_{1}\pm h,x_{2},x_{3}),(x_{1},x_{2}\pm h,x_{3}),(x_{1},x_{2},x_{3}\pm h), gdje je sa h\gt 0 zadan pomak (ove mogućnosti prikazane su na slici 9). Označimo sa f(r,t) vjerojatnost da je čestica, krenuvši iz točke r=(0,0,0) (u trenutku t=0), nakon N pomaka (tj. u vremenu t=N\tau) postigla poziciju r=(N_{1}h,N_{2}h,N_{3}h). Tada, uz interpretaciju kao u (24), vrijedi: gdje su e_{1}=(1,0,0), e_{2}=(0,1,0) i e_{3}=(0,0,1) vektori standardne baze od \mathbb{R}^{3}.

Opišimo sada granično ponašanje ovakvog kretanja, odnosno što se događa kada vrijednost pomaka h i vremenski parametar \tau teže prema 0. Uz odgovarajuće pretpostavke na f, razvojem u Taylorov red dobivamo: Uvrštavanjem dobivenih izraza u (25) i prethodno oduzimanjem f(x,t) od svake strane jednadžbe dobivamo: Označimo \Delta f := \sum_{i=0}^{3}\partial^{2}_{x_{i}}f(r,t) (prisjetimo se, \Delta je Laplaceov operator, definiran prethodno kod (13)). Ako sada pustimo da N\to\infty, i to uz uvjet da N\tau=O(1) i h^{2}/\tau\rightarrow 6D, dobivamo jednažbu



Vratimo se ponovno na simetričnu slučajnu šetnju (S_{n}:n\in\mathbb{N}) određenu kretanjem čestice na pravcu u smjeru lijevo ili desno za vrijednost h kako bismo razmatranja iz prethodnog poglavlja, vezana uz granično ponašanje kada \tau i h teže prema 0 interpretirali pomoću drugog vjerojatnosnog rezultata. Prisjetimo se, distribucija slučajne varijable X_{n} dana je s (23) te vrijedi \mathbb{E}X_{n}=0 i \text{Var}X_{n}=h^{2}. Vjerojatnost f(x,t) promatrana u 5. zapravo je vrijednost funkcije gustoće slučajne varijable S_{n}=\sum_{k=1}^{n}X_{k} u točki x, očekivanje ove slučajne varijable iznosi 0, a varijanca nh^{2}. Prema centralnom graničnom teoremu, slučajna varijabla S_{n}/\sqrt{\text{Var}(S_{n})} uz dovoljno velik n imat će približno jediničnu normalnu razdiobu. Ako n\to\infty, \tau\to 0, h\to 0, uz zahtjev da n\tau=t teži konstanti i \frac{h^{2}}{\tau}\to D, distribuciju od X_{\tau}(t)=S_{t/\tau}=\sum_{k=1}^{t/\tau}X_{k} moći ćemo aproksimirati normalnom distribucijom N(0,Dt), čija je gustoća dana s Prisjetimo se da je ovo upravo funkcija koja se javlja kod rješenja jednadžbe koja opisuje Brownovo gibanje na temelju Einstenovog argumenta. Ovime smo (naravno, samo neformalno) predstavili dio argumenta da je granični proces koji se javlja kod slučajne šetnje slučajni proces koji se naziva Brownovo gibanje. Ovakav slučajni proces prvi je konstruirao Norbert Wiener15, a standardni Wienerov proces ili standardno Brownovo gibanje je (neprekidni) slučajni proces (W_{t}:t\geqslant 0) sa sljedećim svojstvima:

(i)	W_{0}=0 i funkcija t\to W(t) je neprekidna, g.s.;
(ii)	za bilo koje t_{0}\lt t_{1}\lt \ldots\lt t_{n} prirasti W_{t_{i}}-W_{t_{i-1}} su nezavisni;
(iii)	za bilo koje t,s\geqslant 0W_{t+s}-W_{s} ima normalnu razdiobu s parametrima 0 i t.

Uočimo također da smo u gornjem primjeru mogli primijeniti de Moivre-Laplaceov teorem, no primjena općenitije verzije centralnog-graničnog teorema (na primjer, Lévyjevog) omogućila bi isti zaključak i ako izbacimo (možda ne toliko realističnu) pretpostavku da se čestica kreće u određenim smjerovima te s istim vjerojatnostima.

Vratimo se sada na ponovno na trajektorije simetrične slučajne šetnje s pomakom 1 prikazane na slici 10. Možemo uočiti da slika donekle podsjeća na nekakva financijska kretanja (npr. kretanje cijena dionica). Ako zamislimo najjednostavniji model, u kojemu bi u svakom trenutku ta cijena mogla porasti za 1 ili pasti za -1, onda takav model djeluje razumno. No, može li stohastički proces zaista opisati financijska kretanja? Louis Bachelier16 smatra se utemeljiteljem primjene stohastičkih procesa u ekonomiji. U svojoj disertaciji \emph {“Theory of Speculation”} 1900. godine postavio je temelje onog što se danas naziva problem vrednovanja opcija (engl. option pricing problem). Bachelier tvrdi da bi male fluktuacije cijene dionica uočene u kratkom vremenskom intervalu trebale biti neovisne o trenutnoj vrijednosti cijene. Implicitno, također pretpostavlja da su neovisne o ponašanju procesa u prošlosti te u kombinaciji sa centralnim graničnim teoremom zaključuje da su prirasti procesa nezavisni i normalno distribuirani (prisjetimo se ovdje argumenta s početka ovog poglavlja te svojstava (i)-(iii) iz definicije standardnog Wienerovog procesa). Bachelier je u radu uveo pojam tzv. “radijacije” vjerojatnosti, analogne Fourierovom zakonu provođenja topline (“Each price x during an element of time radiates towards its neighboring price an amount of probability proportional to the difference of their probabilities”, [1]). U skladu s tim, za vjerojatnost p cijene x u trenutku t vrijedi p=-\frac{\partial \mathcal{P}}{\partial x}, gdje je \mathcal{P} vjerojatnost da cijena premaši vrijednost x, a vjerojatnost promjene cijene kroz x u vremenskom intervalu \Delta t modelirao je pomoću parcijalne diferencijalne jednažbe uočimo da je ovo ponovno Fourierova jednadžba provođenja topline.

Iako se danas Bachelierov rad smatra radom koji je opisao problem opcija metodom ispred svojeg vremena, trebalo je pola stoljeća da taj rad bude prepoznat; u području matematičke ekonomije to se dogodilo tek primjenom Paula A. Samuelsona17 60-tih godina prošlog stoljeća. U međuvremenu je Bachelierov rad utjecao na rad japanskog matematičara Itô-a18 u teoriji slučajnih procesa, koji je postao temelj za primjenu ekonomista Roberta C. Mertona19 u području matematičkih financija. Na temelju rada Mertona, ekonomisti Myron S. Scholes20 i Fischer Black21 1973. godine opisuju model za vrednovanje opcija, a godine 1997. za ovaj model Mertonu i Scholesu dodjeljena je Nobelova nagrada za ekonomiju.

Opcije spadaju u tzv. izvedene vrijednosne papire, jer njihova isplata ovisi o vrijednosti vezane imovine (vrijednosnog papira, npr. dionice). Kao što je sugerirano nazivom, vlasnik opcije ima mogućnost (ali ne i obvezu) da na unaprijed određeni datum ili ranije (ovisno o vrsti) iskoristi pravo na kupnju (u slučaju call opcije) ili prodaju (u slučaju put opcije) vezane imovine.