Stabilna konvergencija slučajnih varijabli
Sažetak
\mathcal{G}-stabilna konvergencija posebna je vrsta konvergencije slučajnih varijabli koja predstavlja proširenje klasične konvergencije po distribuciji. \mathcal{G}-stabilna konvergencija se pokazala veoma korisnom u teoriji vjerojatnosti, a primjenjuje se i u drugim područjima matematike. Cilj ovog rada je predstaviti i opisati stabilnu konvergenciju slučajnih varijabli, predstaviti neka svojstva ove vrste konvergencije te neke njene korisne posljedice, dodatno ilustrirane primjerima i simulacijama.Ključne riječi: stabilna konvergencija, miješana konvergencija, slaba konvergencija, Markovljeva jezgra, uvjetna distribucija, konvergencija po distribuciji.
1Uvod
Konvergencija nekog niza slučajnih varijabli ključan je pojam u području teorije vjerojatnosti i matematičke statistike. Postoje različite vrste konvergencije nekog niza slučajnih varijabli, a osnovne i one najpoznatije su: konvergencija gotovo sigurno, konvergencija po vjerojatnosti, konvergencija u prostoru L^{p} i konvergencija po distribuciji. Konvergencija po distribuciji, premda najslabija od ova četiri tipa konvergencije, od velike je važnosti budući da pruža uvid u asimptotsko ponašanje slučajnih varijabli te ima fundamentalnu ulogu u graničnim teoremima s ciljem utvrđivanja ponašanja uzoračkih statistika s porastom veličine uzorka.
Iako se obično iskazuju u terminima konvergencije po distribuciji, mnogi granični teoremi uz iste pretpostavke vrijede i u terminima nešto jače vrste konvergencije slučajnih varijabli, što otvara mogućnost dobivanja dodatnih rezultata koji nisu dostupni putem klasične konvergencije po distribuciji. Ta se konvergencija naziva stabilnom konvergencijom slučajnih varijabli, odnosno općenitije \mathcal{G}-stabilnom konvergencijom slučajnih varijabli.
Jedna od važnijih posljedica \mathcal{G}-stabilne konvergencije je takozvani generalizirani Cram\'er-Slutskyjev teorem. Klasična verzija Cram\'er-Slutskyjevog teorema kaže da ako neki niz slučajnih varijabli (X_{n})_{n} konvergira po distribuciji ka slučajnoj varijabli X te ako neki drugi niz slučajnih varijabli (Y_{n})_{n} konvergira prema konstanti c, tada i niz (X_{n}Y_{n})_{n} konvergira po distribuciji i to prema slučajnoj varijabli cX. Važnost ovog teorema leži u tome što pomoću njega često dolazimo do vrlo korisnih asimptotskih rezultata. Kada bismo u iskazu teorema konstantu c mogli zamijeniti slučajnom varijablom, tada bismo na isti način i u mnogim drugim situacija mogli doći do nekih zanimljivih rezultata. Iako ovaj teorem ne vrijedi kada je limes konvergencije po vjerojatnosti općenita slučajna varijabla, ovdje će nam kao odgovarajuće rješenje poslužiti upravo \mathcal{G}-stabilna konvergencija te ćemo uz pomoć te generalizirane verzije spomenutog teorema u mnogim situacijama moći doći do željenih rezultata.
2Definicija i osnovne karakterizacije stabilne konvergencije
Stabilna konvergencija nekog niza slučajnih varijabli definira se pomoću koncepta slabe konvergencije tzv. uvjetnih distribucija slučajnih varijabli uz danu \sigma-algebru. Za početak krenimo od pojma slabe konvergencije niza vjerojatnosnih mjera.
Definicija 2.1. Neka su \mu,\mu_{1},\mu_{2},\dots konačne mjere na \mathcal{B}(\mathbb{R}). Kažemo da niz (\mu_{n})_{n} slabo konvergira prema \mu ako vrijedi:
\begin{align*} \lim_{n}\int g\:d\mu_{n}=\int g\:d\mu,\quad\forall g\in C_{b}({\mathbb{R}^{d}}), \end{align*}
pri čemu C_{b}(\mathbb{R}^{d}) označava skup svih neprekidnih i ograničenih funkcija na \mathbb{R}^{d}. Tu konvergenciju označavamo s \mu_{n}\xrightarrow{w}\mu.Prisjetimo se i definicije konvergencije po distribuciji. Kažemo da niz (X_{n})_{n} slučajnih varijabli konvergira po distribuciji prema slučajnoj varijabli X ako je
(1)
\begin{align} \lim_{n}F_{X_{n}}(x)=F_{X}(x),\quad x\in C(F_{X}), \end{align}
Na relaciju (
Definicija 2.2. Preslikavanje K : \Omega \times \mathcal{B}(\mathbb{R}^{d}) \rightarrow [0,1] takvo da vrijedi:
zovemo Markovljevom jezgrom s (\Omega, \mathcal{F}) u (\mathbb{R}^{d},\mathcal{B}(\mathbb{R}^{d}))}.
| (1) | K(\omega, \cdot) je vjerojatnosna mjera na (\mathbb{R}^{d},\mathcal{B}(\mathbb{R}^{d}))\forall \omega \in \Omega; |
| (2) | K(\cdot, B) je \mathcal{F}-izmjerivo preslikavanje, \forall B\in\mathcal{B}(\mathbb{R}^{d}); |
Skup svih Markovljevih jezgri s (\Omega, \mathcal{F}) u (\mathbb{R}^{d},\mathcal{B}(\mathbb{R}^{d})) označavamo s \mathcal{K}^{1} = \mathcal{K}^{1}(\mathcal{F}) =\mathcal{K}^{1}(\mathcal{F},\mathbb{R}^{d}). Za \sigma-podalgebru \mathcal{G}\subset\mathcal{F} s \mathcal{K}^{1}(\mathcal{G})=\mathcal{K}^{1}(\mathcal{G},\mathbb{R}^{d})\subseteq\mathcal{K}^{1} označavamo skup svih \mathcal{G}-izmjerivih Markovljevih jezgri, to jest Markovljevih jezgri s (\Omega, \mathcal{G}) u (\mathbb{R}^{d},\mathcal{B}(\mathbb{R}^{d})).
Definicija 2.3.Neka je (\Omega,\mathcal{F},P) vjerojatnosni prostor, \mathcal{G}\subset\mathcal{F}\sigma-podalgebra od \mathcal{F} i X:\Omega\rightarrow\mathbb{R}^{d} slučajni vektor. Uvjetna distribucija od X uz dano \mathcal{G}, \mathbb{P}_{X|\mathcal{G}}\: je Markovljeva jezgra u \mathcal{K}^{1}(\mathcal{G}) za koju vrijedi:
(2)
\begin{align} \mathbb{P}_{X|\mathcal{G}}(\cdot,B)=\mathbb{P}(X\in B|\mathcal{G}),\quad \mathbb{P}-\text{g.s. za svaki }B\in\mathcal{B}(\mathbb{R}^{d}). \end{align}
Gornji izraz možemo ekvivalentno zapisati i pomoću uvjetnog očekivanja:
(3)
\begin{align} \mathbb{P}_{X|\mathcal{G}}(\cdot,B)=\mathbb{E}\left(\mathbb{1}_{\lbrace X\in B\rbrace }|\mathcal{G}\right),\quad \mathbb{P}-\text{g.s. za svaki }B\in\mathcal{B}(\mathbb{R}^{d}). \end{align}
\delta_{X}:\Omega\times\mathcal{B}(\mathbb{R}^{d})\rightarrow[0,1] s \delta_{X}(\omega):=\delta_{X(\omega)}, odnosno
\begin{align*} \delta_{X}(\omega,B) = \delta_{X(\omega)}(B)=\mathbb{1}_{\lbrace X(\omega)\in B\rbrace } =\begin{cases} 1, &\quad X(\omega)\in B\\ 0, &\quad X(\omega)\notin B \end{cases},\quad B\in\mathcal{B}(\mathbb{R}^{d}). \end{align*}
Takvu Markovljevu jezgru nazivamo Diracovom jezgrom slučajnog vektora X.Prije same definicije \mathcal{G}-stabilne konvergencije, spomenimo još da je uvjetna distribucija \mathbb{P}_{X|\mathcal{G}} karakterizirana tzv. Radon-Nikodymovim jednadžbama:
(4)
\begin{align} \int_{G}\mathbb{P}_{X|\mathcal{G}}(\omega,B)d\mathbb{P}(\omega) = \mathbb{P}(X^{-1}(B)\cap G),\quad\forall G\in\mathcal{G},B\in\mathcal{B}(\mathbb{R}^{d}). \end{align}
Definicija 2.4. Neka je \mathcal{G}\subset\mathcal{F} \sigma-podalgebra of \mathcal{F}. Za niz (X_{n})_{n} d-dimenzionalnih slučajnih vektora kažemo da konvergira \mathcal{G}-stabilno ka slučajnom vektoru X:\Omega\rightarrow\mathbb{R}^{d} ako vrijedi:
U slučaju da granična uvjetna distribucija \mathbb{P}_{X|\mathcal{G}} ne ovisi o \omega\in\Omega, tada kažemo da niz (X_{n})_{n} konvergira \mathcal{G}-miješano prema slučajnom vektoru X. Drugim riječima, to znači da je \mathbb{P}_{X|\mathcal{G}}= \mathbb{P}_{X}, što je ekvivalentno s time da su \sigma(X) i \mathcal{G} nezavisne.
\mathcal{F}-stabilnu i \mathcal{F}-miješanu konvergenciju kraće zovemo stabilnom i miješanom konvergencijom.
\mathbb{P}_{X_{n}|\mathcal{G}}\xrightarrow{w}\mathbb{P}_{X|\mathcal{G}}
kada n\rightarrow\infty, odnosno ako vrijedi:
\begin{align*} \lim_{n}\iint f(\omega)h(x)\mathbb{P}_{X_{n}|\mathcal{G}}(\omega,dx)d\mathbb{P}(\omega)=\iint f(\omega)h(x)\mathbb{P}_{X|\mathcal{G}}(\omega,dx)d\mathbb{P}(\omega) \end{align*}
za svaku apsolutno integrabilnu i \mathcal{F}-izmjerivu funkciju f\in\mathcal{L}^{1}(\Omega,\mathbb{P}) te svaku funkciju h\in C_{b}(\mathbb{R}^{d}). Pišemo: X_{n}\rightarrow X \mathcal{G}-stabilno.U slučaju da granična uvjetna distribucija \mathbb{P}_{X|\mathcal{G}} ne ovisi o \omega\in\Omega, tada kažemo da niz (X_{n})_{n} konvergira \mathcal{G}-miješano prema slučajnom vektoru X. Drugim riječima, to znači da je \mathbb{P}_{X|\mathcal{G}}= \mathbb{P}_{X}, što je ekvivalentno s time da su \sigma(X) i \mathcal{G} nezavisne.
\mathcal{F}-stabilnu i \mathcal{F}-miješanu konvergenciju kraće zovemo stabilnom i miješanom konvergencijom.
Za slučajan vektor X:\Omega\rightarrow\mathbb{R}^{d} i Borel-izmjerivu funkciju h:\mathbb{R}^{d}\rightarrow\mathbb{R}, takvu da je h(X)\in\mathcal{L}^{1}(\Omega,\mathbb{P}), vrijedi:
(5)
\begin{align} \mathbb{E}(h(X)|\mathcal{G})=\int_{\mathbb{R}^{d}} h(x)d\mathbb{P}_{X|\mathcal{G}}(\cdot,x). \end{align}
\mathbb{E}(\mathbb{1}_{B}(X)|\mathcal{G})\overset{(3)}{=}\mathbb{P}_{X|\mathcal{G}}(\cdot,B)=\int_{B} d\mathbb{P}_{X|\mathcal{G}}(\cdot,x)=\int_{\mathbb{R}^{d}}\mathbb{1}_{B}(x)d\mathbb{P}_{X|\mathcal{G}}(\cdot,x).
Jednakost (
\begin{align*} \iint f(\omega)h(x)\mathbb{P}_{X|\mathcal{G}}(\omega,dx)d\mathbb{P}(\omega) &=\int f(\omega)\underbrace{\int h(x)\mathbb{P}_{X|\mathcal{G}}(\omega,dx)}_{\mathbb{E}[h(X)|\mathcal{G}](\omega)}d\mathbb{P}(\omega)=\\ &\overset{(5)}{=}\int f(\omega)\mathbb{E}[h(X)|\mathcal{G}](\omega)d\mathbb{P}(\omega)=\\ &=\mathbb{E}\big(f\:\mathbb{E}[h(X)|\mathcal{G}]\big), \end{align*}
prema tome \mathcal{G}-stabilnu konvergenciju možemo ekvivalentno zapisati na sljedeći način:
(6)
\begin{align} \lim_{n}\mathbb{E}\big(f\:\mathbb{E}[h(X_{n})|\mathcal{G}]\big) = \mathbb{E}\big(f\:\mathbb{E}[h(X)|\mathcal{G}]\big),\quad\forall f\in\mathcal{L}^{1}(\Omega,\mathbb{P}),\:h\in C_{b}(\mathbb{R}^{d}). \end{align}
Idući teorem sadrži osnovne karakterizacije \mathcal{G}-stabilne konvergencije koje u mnogim slučajevima olakšavaju dokaze vezane uz ovu vrstu konvergencije. Sve tvrdnje ovog teorema zapravo su posljedica nešto općenitijeg teorema koji se odnosi na karakterizacije slabe konvergencije Markovljevih jezgri.
Teorem 2.5. Neka su X_{n},X d-dimenzionalni slučajni vektori, n\in\mathbb{N}, \mathcal{E}\subset\mathcal{G} familija zatvorena na konačne presjeke takva da je \Omega\in\mathcal{E} i \sigma(\mathcal{E})=\mathcal{G}.
Tada su sljedeće tvrdnje ekvivalentne:
Tada su sljedeće tvrdnje ekvivalentne:
| (i) | X_{n}\rightarrow X\quad \mathcal{G}-stabilno; |
| (ii) | \lim_{n}\mathbb{E}fh(X_{n}) = \mathbb{E}fh(X) za svaki f\in\mathcal{L}^{1}(\Omega,\mathcal{G},\mathbb{P}) i h\in C_{b}(\mathbb{R}^{d}); |
| (iii) | Q_{X_{n}}\xrightarrow{w} Q_{X} za svaku vjerojatnosnu mjeru Q na \mathcal{F} takvu da je Q\ll \mathbb{P} i dQ/d\mathbb{P} je \mathcal{G}-izmjeriva; |
| (iv) | \mathbb{P}_{F}^{X_{n}}\xrightarrow{w}\mathbb{P}_{F}^{X} za svaki F\in\mathcal{E} takav da je \mathbb{P}(F)\gt 0; |
| (v) | \lim_{n}\int g(\omega, X_{n}(\omega))\:d\mathbb{P}(\omega)=\int g(\omega,X(\omega))\:d\mathbb{P}(\omega) za svaku izmjerivu i ograničenu funkciju g:(\Omega\times\mathbb{R}^{d},\mathcal{G}\otimes\mathcal{B}(\mathbb{R}^{d}))\rightarrow(\mathbb{R},\mathcal{B}(\mathbb{R})) takvu da je g(\omega,\cdot)\in C_{b}(\mathbb{R}^{d}) za svaki \omega\in\Omega; |
| (vi) | (X_{n},Y)\rightarrow (X,Y)\mathcal{G}-stabilno za svaki \mathcal{G}-izmjeriv slučajni vektor Y s vrijednostima u \mathbb{R}^{m}; |
| (vii) | (X_{n},\mathbb{1}_{F})\xrightarrow{d}(X,\mathbb{1}_{F}) za svaki F\in\mathcal{E}. |
Slične ekvivalencije vrijede i za \mathcal{G}-miješanu konvergenciju, a one su upravo posljedica ekvivalencija iz prethodnog teorema. Dokaz ovog teorema i ostalih tvrdnji spomenutih u članku mogu se naći u
2.1Svojstva \mathcal{G}-stabilne konvergencije
Najprije ćemo analizirati odnos \mathcal{G}-stabilne konvergencije i nekih osnovnih tipova konvergencije slučajnih varijabli.
Nije teško pokazati da vrijedi sljedeća implikacija:
\begin{align*} X_{n}\rightarrow X\:\mathcal{G}\text{-stabilno}\implies X_{n}\xrightarrow{d}X. \end{align*}
Dokaz. Ako pretpostavimo da X_{n}\rightarrow X \mathcal{G}-stabilno, tada po definiciji \mathcal{G}-stabilne konvergencije vrijedi:
\begin{align*} \lim_{n}\mathbb{E}\big(f\:\mathbb{E}[h(X_{n})|\mathcal{G}]\big) = \mathbb{E}\big(f\:\mathbb{E}[h(X)|\mathcal{G}]\big),\quad\forall f\in\mathcal{L}^{1}(\Omega,\mathbb{P}),\:h\in C_{b}(\mathbb{R}^{d}). \end{align*}
Budući da gornja jednakost mora vrijediti za svaku funkciju f\in\mathcal{L}^{1}(\Omega,\mathbb{P}), specijalno mora vrijediti i za f=\mathbb{1}_{\Omega}, iz čega slijedi:
\begin{align*} \lim_{n}\mathbb{E}\big(\mathbb{E}[h(X_{n})|\mathcal{G}]\big) = \mathbb{E}\big(\mathbb{E}[h(X)|\mathcal{G}]\big),\quad\forall h\in C_{b}(\mathbb{R}^{d}), \end{align*}
pa zbog svojstva uvjetnog očekivanja \mathbb{E}\big(\mathbb{E}[h(X_{n})|\mathcal{G}]\big )=\mathbb{E}h(X_{n}) slijedi
\begin{align*} \lim_{n}\mathbb{E}h(X_{n}) = \mathbb{E}h(X),\quad\forall h\in C_{b}(\mathbb{R}^{d}). \end{align*}
Prethodnu relaciju sada možemo ekvivalentno zapisati pomoću integrala po odgovarajućim zakonima razdiobe \mathbb{P}_{X_{n}} i \mathbb{P}_{X}:
\begin{align*} \lim_{n}\int h\:d \mathbb{P}_{X_{n}} = \int h\:d\mathbb{P}_{X},\quad\forall h\in C_{b}(\mathbb{R}^{d}). \end{align*}
iz čega vidimo da vrijedi X_{n}\xrightarrow{d}X.
\ \blacksquare
Na analogni način se pokaže i da \mathcal{G}-miješana konvergencija povlači konvergenciju po distribuciji.
U slučaju trivijalne \sigma-podalgebre \mathcal{G}=\lbrace \emptyset, \Omega\rbrace, vrijedi \mathbb{P}_{X_{n}|\mathcal{G}}=\mathbb{P}_{X_{n}}, \forall n\in\mathbb{N} i \mathbb{P}_{X|\mathcal{G}}=\mathbb{P}_{X} pa \mathcal{G}-stabilna konvergencija postaje ekvivalentna konvergenciji po distribuciji.
Također, ekvivalenciju \mathcal{G}-stabilne konvergencije i konvergencije po distribuciji dobivamo i u slučaju da su slučajni vektori X_{n}, X,\:n\in\mathbb{N} nezavisni od \mathcal{G}, to jest ako su \sigma-algebre \sigma(X_{n}) i \sigma(X) nezavisne od \mathcal{G} za svaki n\in\mathbb{N}. Ova tvrdnja trivijalno slijedi iz ekvivalencije
\begin{align*} \mathbb{P}_{X|\mathcal{G}}=\mathbb{P}_{X}\:\iff \sigma(X)\text{ i }\mathcal{G}\text{ su nezavisne.} \end{align*}
Dokaz. Familije \sigma(X) i \mathcal{G} su nezavisne ako vrijedi:
4 ) za \mathbb{P}_{X|\mathcal{G}} imamo:
\mathbb{P}(X^{-1}(B)\cap G )= \mathbb{P}(X^{-1}(B))\mathbb{P}(G),\quad\forall B\in\mathcal{B}(\mathbb{R}^{d}),G\in\mathcal{G}.
S druge strane, iz Radon - Nikodymovih jednadžbi (
\begin{align*} \int_{G}\mathbb{P}_{X|\mathcal{G}}(\omega,B)d\mathbb{P}(\omega) = \mathbb{P}(X^{-1}(B)\cap G),\quad\forall G\in\mathcal{G},B\in\mathcal{B}(\mathbb{R}^{d}). \end{align*}
Ako pretpostavimo da je \mathbb{P}_{X|\mathcal{G}}=\mathbb{P}_{X}, tada je
\begin{align*} \int_{G}\mathbb{P}_{X|\mathcal{G}}(\omega,B)d\mathbb{P}(\omega) &=\int_{G}\int\mathbb{1}_{B}(x)\mathbb{P}_{X|\mathcal{G}}(\omega,dx) d\mathbb{P}(\omega) = \int_{G}\int\mathbb{1}_{B}(x)d\mathbb{P}_{X}(x) d\mathbb{P}(\omega)=\\ &=\int_{G} \mathbb{P}_{X}(B)d\mathbb{P} = \mathbb{P}_{X}(B)\mathbb{P}(G)= \mathbb{P}(X^{-1}(B))\mathbb{P}(G). \end{align*}
Tvrdnja sada slijedi kombiniranjem prethodne tri relacije i g.s. jedinstvenosti uvjetne distribucije \mathbb{P}_{X|\mathcal{G}}.
\ \blacksquare
(7)
\begin{align} X_{n}\rightarrow X\:\mathcal{G}\text{-stabilno}\iff X_{n}\xrightarrow{\mathbb{P}}X. \end{align}
Dokaz.
\ \blacksquare
Ako u ekvivalenciji (
Budući da trivijalna \sigma-algebra \mathcal{G} reducira \mathcal{G}-stabilnu konvergenciju do konvergencije po distribuciji, a \sigma(X)\subset\mathcal{G} ju čini ekvivalentnom konvergenciji po vjerojatnosti, na \mathcal{G}-stabilnu konvergenciju možemo gledati kao na tip konvergencije "između" konvergencije po distribuciji i konvergencije po vjerojatnosti. Dijagram odnosa osnovnih tipova konvergencije sada možemo upotpuniti kao što je prikazano na slici dolje.
Slika 1: Dijagram odnosa osnovnih tipova konvergencije.
3Posljedice i primjena \mathcal{G}-stabilne konvergencije
Kao što je spomenuto u uvodnom dijelu, stabilna konvergencija će nam omogućiti nešto općenitiju verziju Cramér-Slutskyjevog teorema. Za početak promotrimo klasičnu verziju ovog teorema:
Teorem 3.1. (Cramér-Slutsky [12] ) Neka su (X_{n})_{n} i (Y_{n})_{n} nizovi realnih slučajnih varijabli i X realna slučajna varijabla. Pretpostavimo da su sve one definirane na istom vjerojatnosnom prostoru (\Omega,\mathcal{F},\mathbb{P}) te neka je c\in\mathbb{R}. Tada vrijedi:
X_{n}\xrightarrow{d}X,\;Y_{n}\xrightarrow{\mathbb{P}}c\;\implies X_{n} Y_{n}\xrightarrow{d} c X.
Ovaj teorem predstavlja vrlo koristan alat za dobivanje različitih asimptotskih rezultata. To možemo lako vidjeti na primjeru klasičnog centralnog graničnog teorema:
Neka je(X_{n})_{n} niz nezavisnih, jednako distribuiranih slučajnih varijabli s očekivanjem \mu\in\mathbb{R} te s konačnom varijancom \sigma^{2}\in \langle 0,+\infty\rangle. Tada vrijedi:
(9)
\begin{align} \frac{\overline{X_{n}}-\mu}{\sigma}\sqrt{n}\overset{d}{\rightarrow}N(0,1). \end{align}
Niz procjenitelja (\hat{\sigma}_{n}^{2})_{n} od \sigma^{2}, definiran s \hat{\sigma}_{n}^{2}:=\frac{1}{n}\sum_{k=1}^{n} (X_{k}-\overline{X}_{n})^{2},\; n\in\mathbb{N} je jako konzistentan niz procjenitelja, to jest vrijedi \hat{\sigma}_{n}^{2}\xrightarrow{g.s.}\sigma^{2}.
Stoga, iz (
\frac{\overline{X_{n}}-\mu}{\hat{\sigma}_{n}}\sqrt{n}\overset{d}{\rightarrow}N(0,1).
Sada je jedina nepoznanica parametar očekivanja \mu, stoga nam prethodna relacija daje da je niz procjenitelja za \mu, (\overline{X}_{n})_{n} asimptotski normalan s očekivanjem \mu i varijancom \frac{\hat{\sigma}_{n}^{2}}{n}. Ovakav nam je rezultat veoma koristan budući da iz njega sada možemo donositi zaključke o asimptotskom ponašanju niza aritmetičkih sredina slučajnih uzoraka ili, primjerice, konstruirati intervale pouzdanosti za parametar \mu.Ovdje smo mogli upotrijebiti klasičan Cramér-Slutskyjev teorem budući da je limes konvergencije gotovo sigurno konstanta \sigma^{2}, a budući da konvergencija gotovo sigurno povlači konvergenciju po vjerojatnosti, zadovoljene su sve pretpostavke teorema. Međutim, u mnogim situacijama to neće biti slučaj.
Iako Cramér-Slutskyjev teorem ne vrijedi ako graničnu konstantu zamijenimo slučajnom varijablom, upravo će se stabilna konvergencija pokazati kao odgovarajuće rješenje u mnogim takvim situacijama. Konkretno, sljedeći teorem nam omogućuje tzv. generaliziranu verziju Cramér-Slutskyjevog teorema.
Teorem 3.2. Neka su X_{n},X d-dimenzionalni slučajni vektori, X_{n}\rightarrow X \mathcal{G}-stabilno te neka su Y_{n},Y m-dimenzionalni slučajni vektori pri čemu je d,m\in\mathbb{N}. Tada vrijedi:
| (i) | Neka je d = m. Ako \Vert X_{n}-Y_{n}\Vert \xrightarrow{\mathbb{P}}0, tada Y_{n}\rightarrow X \mathcal{G}-stabilno. |
| (ii) | Ako Y_{n}\xrightarrow{\mathbb{P}}Y i Y je \mathcal{G}-izmjeriva, tada (X_{n},Y_{n})\rightarrow(X,Y) \mathcal{G}-stabilno. |
| (iii) | Ako je g:\mathbb{R}^{d}\rightarrow\mathbb{R}^{m} Borel-izmjeriva i \mathbb{P}_{X}-g.s. neprekidna funkcija, tada g(X_{n})\rightarrow g(X) \mathcal{G}-stabilno. |
Pretpostavimo da su (X_{n})_{n} i (Y_{n})_{n} nizovi realnih slučajnih varijabli takvi da X_{n}\rightarrow X\mathcal{G}-stabilno te Y_{n}\xrightarrow{\mathbb{P}}Y, gdje je Y\mathcal{G}-izmjeriva slučajna varijabla. Prema tvrdnji (ii) slijedi da (X_{n},Y_{n})\rightarrow(X,Y)\mathcal{G}-stabilno, a zatim iz tvrdnje (iii) slijedi X_{n}Y_{n}\rightarrow XY\;\mathcal{G}\text{-stabilno.}
Dakle, vrijedi generalizirana verzija Cramér-Slutskyjevog teorema:
Teorem 3.3. Neka su (X_{n})_{n} i (Y_{n})_{n} nizovi realnih slučajnih varijabli, X i Y realne slučajne varijable te neka je Y\mathcal{G}-izmjeriva. Pretpostavimo da su sve one definirane na istom vjerojatnosnom prostoru (\Omega,\mathcal{F},\mathbb{P}). Tada vrijedi:
Ovaj ćemo rezultati primijeniti na iduća dva primjera te time demonstrirati njegovu značajnost.
X_{n}\rightarrow X\;\mathcal{G}\text{-stabilno}\quad\text{i}\quad Y_{n}\xrightarrow{\mathbb{P}}Y\:\implies\: X_{n}Y_{n}\rightarrow XY\:\mathcal{G}\text{-stabilno.}
Primjer 3.4. (Galton - Watsonov proces grananja) Neka je (Y_{i}^{n})_{i,n} familija nezavisnih jednako distribuiranih slučajnih varijabli definiranih na vjerojatnosnom prostoru (\Omega, \mathcal{F},\mathbb{P}) s vrijednostima u \mathbb{Z}_{+}, pri čemu je i,n\ge 1. Niz (Z_{n})_{n\ge 0} definiran s Z_{0}:=1 te
\begin{align*} Z_{n} := \begin{cases} Y_{1}^{n}+\dots + Y_{Z_{n-1}}^{n}, &\quad\text{ako je }Z_{n-1}\gt 0\\ 0, &\quad\text{inače} \end{cases},n\in\mathbb{N} \end{align*}
zovemo jednostavnim ili Galton-Watsonovim procesom grananja. Z_{n} interpretiramo kao broj jedinki u n-toj generaciji, a Y_{i}^{n} kao broj potomaka u n-toj generaciji nastao od i-tog potomka iz prethodne generacije.Slučajne varijable Y_{i}^{n}, Y_{1}^{1} i Z_{1} su jednako distribuirane za svaki n\in\mathbb{N}, Y_{i}^{n}\sim Y_{1}^{1}\sim Z_{1}. S \mu ćemo označiti očekivani broj potomaka jedne jedinke, to jest \mu = \mathbb{E}(Y_{i}^{n})= \mathbb{E}(Z_{1}). U ovom primjeru je \mu parametar od interesa, a cilj je definirati neki niz procjenitelja za \mu te analizirati njegovo asimptotsko ponašanje.
Lako se pokaže da je očekivani broj potomaka u n-toj generaciji
\mathbb{E}(Z_{n}) = \mu^{n}.
Dokazi ove i drugih općenitijih tvrdnji na koje se pozivamo u ovom primjeru mogu se pronaći u Dodatno ćemo pretpostaviti da je \mu \gt 1 te da vrijedi \lim_{n} Z_{n} = +\infty g.s. Definirajmo sada slučajni proces X=(X_{n})_{n} s
X_{n} := \frac{Z_{n}}{\mu^{n}},\quad n\ge 0.
Ovako definiran slučajni proces je nenegativan martingal, a za takve slučajne procese vrijedi da konvergiraju gotovo sigurno prema nekoj slučajnoj varijabli X_{\infty} konačnog očekivanja. Dakle, imamo
(10)
\begin{align} \lim_{n} X_{n} = X_{\infty}\quad g.s. \end{align}
(11)
\begin{align} \lim_{n}\frac{\mu-1}{\mu^{n}}\sum_{j=1}^{n} Z_{j-1} = X_{\infty}\quad g.s. \end{align}
Označimo s
\hat{\mu}_{n}^{(H)}:=\frac{\sum_{i=1}^{n} Z_{i}}{\sum_{i=1}^{n} Z_{i-1}}
procjenitelj od \mu. Taj procjenitelj se naziva Harrisov procjenitelj od \mu. Može se pokazati da je (\hat{\mu}_{n}^{(H)})_{n} konzistentan niz procjenitelja od \mu, to jest da vrijedi \hat{\mu}_{n}^{(H)}\xrightarrow{\mathbb{P}}\mu, vidi Za ovaj niz procjenitelja se uz pomoć stabilne konvergencije pokazuje da vrijedi sljedeće (
(12)
\begin{align} \frac{\mu^{\frac{n}{2}}}{(\mu - 1)^{\frac{1}{2}}}(\hat{\mu}_{n}^{(H)}-\mu)\rightarrow\sigma X_{\infty}^{-\frac{1}{2}}N\quad\mathcal{F}_{\infty}\text{-stabilno,} \end{align}
Budući da stabilna konvergencija povlači konvergenciju po distribuciji, vrijedi i sljedeći rezultat
(13)
\begin{align} \frac{\mu^{\frac{n}{2}}}{(\mu-1)^{\frac{1}{2}}}(\hat{\mu}_{n}^{(H)}-\mu)\xrightarrow{d}\sigma X_{\infty}^{-\frac{1}{2}}N. \end{align}
\left(\sum_{j=1}^{n} Z_{j-1}\right)^{\frac{1}{2}}(\hat{\mu}_{n}^{(H)}-\mu)\rightarrow\sigma N\quad\mathcal{F}_{\infty}\text{-miješano}
te posljedično
\left(\sum_{j=1}^{n} Z_{j-1}\right)^{\frac{1}{2}}(\hat{\mu}_{n}^{(H)}-\mu)\xrightarrow{d}\sigma N(0,1).
Dakle, (\hat{\mu}_{n}^{(H)})_{n} je asimptotski normalan niz procjenitelja s očekivanjem \mu i standardnom devijacijom \frac{\sigma}{\left(\sum_{j=1}^{n} Z_{j-1}\right)^{\frac{1}{2}}}.Ilustrirajmo ovaj rezultat simulacijama.
Definirajmo familiju nezavisnih jednako distribuiranih slučajnih varijabli (Y_{i}^{n})_{i,n} na sljedeći način:
Y_{i}^{n} := V_{i}^{n}+2\quad i\ge1, n\ge 1,
pri čemu je (V_{i}^{n})_{i,n} niz nezavisnih jednako distribuiranih slučajnih varijabli s Poissonovom razdiobom V_{i}^{n}\sim \text{Pois}(1.5), \:i,n\ge 1.Definirajmo sada jednostavni proces grananja (Z_{n})_{n\ge0} pomoću familije (Y_{i}^{n}). Iz svojstava matematičkog očekivanja i varijance lagano slijedi
\mu =\mathbb{E}(Y_{i}^{n})=\mathbb{E}(V_{i}^{n}+2)=\mathbb{E}(V_{i}^{n})+2 = 1.5 + 2 = 3.5
te
\sigma^{2} = \text{Var}(Y_{i}^{n}) = \text{Var}(V_{i}^{n}+2) = \text{Var}(V_{i}^{n})=1.5.
Nadalje, budući da Y_{i}^{n} predstavlja broj potomaka jedne jedinke, Y_{i}^{n} po svojoj definiciji poprima vrijednosti u skupu \lbrace 2,3,\dots\rbrace za svaki i,n\in\mathbb{N} pa će u svakoj generaciji broj jedinki biti nužno veći od broja jedinki prethodne generacije. Dakle, populacija beskonačno raste te su zadovoljene sve pretpostavke s početka ovog primjera.Generirat ćemo n = 100, 500 i 1000 uzoraka koji predstavljaju proces grananja (Z_{n})_{n} do generacije N=15 (populacija jako brzo raste pa je već u petnaestoj generaciji ukupan broj jedinki u populaciji reda veličine 10^{7} odnosno 10^{8}), te ćemo za svaki uzorak izračunati Harrisov procjenitelj \hat{\mu}_{N}^{(H)} parametra \mu. Očekujemo da će s porastom broja generiranih trajektorija procesa grananja uzorak pripadnih Harrisovih procjenitelja postajati sve "normalniji".
Za n = 100 generiranih trajektorija procesa grananja dobivamo uzorak od 100 Harrisovih procjenitelja (\hat{\mu}^{(H)}_{N,n})_{n},\; n =1,\dots,100. Lillieforsov test proveden nad tim uzorkom daje p-vrijednost od 0.1198, stoga ne odbacujemo nultu hipotezu o normalnosti uzorka niti na jednoj standardnoj razini značajnosti.
Histogram realizacija uzorka procjenitelja prikazan je na Slici 2 zajedno s funkcijom gustoće normalne razdiobe s procijenjenim parametrima očekivanja i standardne devijacije te s procijenjenom funkcijom gustoće.
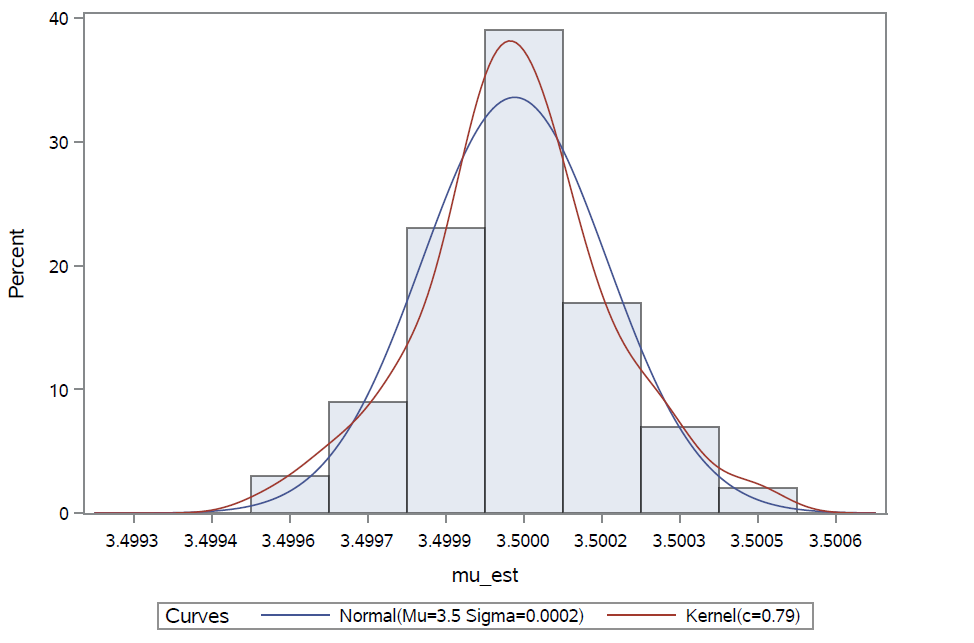
Slika 2: Distribucija Harrisovih procjenitelja za n = 100.
Iz slike je jasno da histogram dobro prati graf funkcije gustoće normalne razdiobe, a osim toga aritmetička sredina uzorka (\hat{\mu}^{(H)}_{N,n})_{n} iznosi 3.500007 što je gotovo jednako egzaktnoj vrijednosti parametra \mu koja je jednaka 3.5. Nadalje, ako za svaku od 100 generiranih trajektorija procesa grananja odredimo vrijednost od \sigma /\sqrt{\sum_{j=1}^{N} Z_{j-1}} te potom uzmemo aritmetičku sredinu tih vrijednosti, ona iznosi 0.000184, što je približno jednako uzoračkoj standardnoj devijaciji niza (\hat{\mu}^{(H)}_{N,n})_{n} koja iznosi 0.000178. Dakle, za 100 generiranih trajektorija procesa grananja do 15-te generacije, distribucija realizacija Harrisovih procjenitelja je približno jednaka N(3.5, 0.000184^{2}). Očekujemo da će za n = 500 distribucija uzorka Harrisovih procjenitelja biti još bliža normalnoj razdiobi.
Za n=500 p-vrijednost Lillieforsovog testa je nešto veća od p-vrijednosti u prethodnom slučaju, i iznosi 0.1876. Dakle, ponovo ne odbacujemo pretpostavku normalnosti.
Histogram prikazan na Slici 3 još bolje prati graf funkcije gustoće normalne razdiobe s procijenjenim parametrima, a oni su ponovo jako blizu očekivanim vrijednostima: aritmetička sredina uzorka (\hat{\mu}^{(H)}_{N,n})_{n} iznosi 3.500008, a standardna devijacija je jednaka 0.000175.

Slika 3: Distribucija Harrisovih procjenitelja za n = 500.
Promotrimo još slučaj kada je n = 1000. Ponovo, ne odbacujemo pretpostavku normalnosti (p-vrijednost Lillieforsovog testa iznosi 0.215). Izgled histograma, prikazan na Slici 4, upućuje na još veću normalnost u podacima nego ranije.
Dakle, možemo zaključiti da s porastom duljine uzorka procesa grananja, distribucija pripadnih realizacija Harrisovih procjenitelja postaje sve bliža normalnoj distribuciji s parametrima \mu i \sigma /\sqrt{\sum_{j=1}^{N} Z_{j-1}}.

Slika 4: Distribucija Harrisovih procjenitelja za n = 1000.
\ \blacksquare
Još jedna važna posljedica stabilne konvergencije je verzija centralnog graničnog teorema za martingale. Ta je generalizacija nadahnuta Lindebergovom verzijom centralnog graničnog teorema koja ne zahtijeva jednaku distribuiranost slučajnih varijabli, već samo nezavisnost te da vrijedi tzv. Lindebergov uvjet.
Uvjetna verzija Lindebergovog uvjeta ima ključnu ulogu u stabilnom martingalnom centralnom graničnom teoremu.Taj ćemo teorem iskazati za slučajni proces X=(X_{n})_{n} definiran s
X_{n}:=Y_{n}-Y_{n-1},\;n\in\mathbb{N},
pri čemu je (Y_{n})_{n\ge 0} martingal adaptiran obzirom na filtraciju \mathbb{F}. Takav slučajni proces X zovemo nizom martingalnih razlika. Za njega vrijedi:
\mathbb{E}(X_{n+1}|\mathcal{F}_{n})=0\; g.s.
za svaki n\ge 1 te je i sam adaptiran obzirom na filtraciju \mathbb{F}.
Teorem 3.5. (Stabilni martingalni centralni granični teorem [10] ) Neka je X=(X_{k})_{k} niz martingalnih razlika adaptiran obzirom na filtraciju \mathbb{F}=(\mathcal{F}_{n})_{n\ge 0} te neka je (a_{n})_{n} niz pozitivnih realnih brojeva takav da a_{n}\rightarrow +\infty.
Ako su zadovoljeni uvjeti:
ili ako je (X_{k})_{k} kvadratno integrabilan slučajni proces te vrijede uvjeti: [label=(\roman*)]
tada vrijedi:
Ako su zadovoljeni uvjeti:
| (i) | \frac{1}{a_{n}^{2}}\sum_{k=1}^{n} X_{k}^{2}\xrightarrow{\mathbb{P}} Z^{2}; |
| (ii) | \frac{1}{a_{n}}\mathbb{E}\left(\max_{1\le k\le n}|X_{k}|\right)\rightarrow0 kada n\rightarrow + \infty; |
| (iii) | \frac{1}{a_{n}^{2}}\sum_{k=1}^{n} \mathbb{E}\left(X_{k}^{2}|\mathcal{F}_{k-1}\right)\xrightarrow{\mathbb{P}}Z^{2}; |
| (iv) | \frac{1}{a_{n}^{2}}\sum_{k=1}^{n}\mathbb{E}\left(X_{k}^{2}\mathbb{1}_{\lbrace |X_{k}|\ge\epsilon a_{n}\rbrace }|\mathcal{F}_{k-1}\right)\xrightarrow{\mathbb{P}}0,\quad \forall\epsilon\gt 0\quad (uvjetni Lindebergov uvjet); |
\frac{1}{a_{n}}\sum_{k=1}^{n} X_{k}\rightarrow ZN\quad\mathcal{F}_{\infty}\text{-stabilno},
pri čemu je Z neka nenegativna realna slučajna varijabla te N\sim N(0,1) nezavisna od \mathcal{F}_{\infty}.Ovaj teorem ima brojne zanimljive posljedice, a jedna od njih dana je u sljedećem primjeru.
Primjer 3.6. Neka je X=(X_{n})_{n} niz martingalnih razlika adaptiran obzirom na prirodnu filtraciju \mathbb{F}^{0}=\lbrace \mathcal{F}_{n}^{0}:\:n\ge 0\rbrace od X, gdje je \mathcal{F}_{0}^{0}= \lbrace \emptyset,\Omega\rbrace, \mathcal{F}_{n}^{0}= \sigma(X_{1},\dots,X_{n}). Označimo \mathcal{F_{\infty}}=\sigma\left(\bigcup_{n=0}^{\infty} \mathcal{F}_{n}^{0}\right). Pretpostavimo da je X stacionaran slučajni proces, to jest da za svaki k\ge 1 i svaki n\ge 1 vrijedi:
(X_{1},\dots,X_{k})\overset{d}{=}(X_{n+1},\dots,X_{n+k}),
te da je X_{1}\in\mathcal{L}^{1}(\Omega,\mathbb{P}).Pod ovim pretpostavkama, iz tzv. Birkhoffove verzije Ergodskog teorema
(14)
\begin{align} \frac{1}{n}\sum_{k=1}^{n}X_{k}^{2}\xrightarrow{g.s.}\mathbb{E}(X_{1}^{2}|\mathcal{I}_{X}), \end{align}
Ako stavimo a_{n}=\sqrt{n},\:n\in\mathbb{N}, tada iz (
\frac{1}{n}\sum_{k=1}^{n}\mathbb{E}(X_{k}^{2}\mathbb{1}_{\lbrace |X_{k}|\ge\epsilon \sqrt{n}\rbrace })=\mathbb{E}(X_{1}^{2}\mathbb{1}_{\lbrace |X_{1}|\ge\epsilon\sqrt{n}\rbrace })\xrightarrow{n\rightarrow\infty}0,
iz čega dalje slijedi
\begin{align*} \left(\frac{1}{\sqrt{n}}\mathbb{E}\left(\max_{1\le k \le n}|X_{k}|\right)\right)^{2}&\le\frac{1}{n}\mathbb{E}\left(\max_{1\le k\le n} X_{k}^{2}\right)\le\frac{1}{n}\mathbb{E}\left(\max_{1\le k\le n} X_{k}^{2}\mathbb{1}_{\lbrace |X_{k}|\ge\epsilon \sqrt{n}\rbrace }\right)+\\ &\quad+\frac{1}{n}\underbrace{\mathbb{E}\left(\max_{1\le k\le n} X_{k}^{2}\mathbb{1}_{\lbrace |X_{k}|\lt \epsilon \sqrt{n}\rbrace }\right)}_{\lt \epsilon^{2}n}\le\\ &\le \frac{1}{n}\sum_{k=1}^{n}\mathbb{E}(X_{k}^{2}\mathbb{1}_{\lbrace |X_{k}|\ge\epsilon \sqrt{n}\rbrace })+\epsilon^{2}\xrightarrow{n\rightarrow\infty}0, \end{align*}
jer je \epsilon\gt 0 proizvoljan.Dakle, prema Teoremu 3.5 vrijedi:
(15)
\begin{align} \frac{1}{\sqrt{n}}\sum_{k=1}^{n}X_{k}\rightarrow\mathbb{E}(X_{1}^{2}|\mathcal{I}_{X})^{\frac{1}{2}}N\quad\mathcal{F}_{\infty}\text{-stabilno.} \end{align}
\left(\sum_{k=1}^{n}X_{k}^{2}\right)^{-\frac{1}{2}}\sum_{k=1}^{n}X_{k}\rightarrow N\;\mathcal{F}_{\infty}\text{-stabilno,}
odnosno
(16)
\begin{align} \left(\sum_{k=1}^{n}X_{k}^{2}\right)^{-\frac{1}{2}}\sum_{k=1}^{n}X_{k}\xrightarrow{d} N(0,1). \end{align}
Pogledajmo ovaj rezultat na konkretnom primjeru.
Neka je X=(X_{n})_{n} niz nezavisnih jednako distribuiranih slučajnih varijabli, X_{n}\sim N(0,\sigma^{2}),n\ge 1. Za niz X vrijedi:
\mathbb{E}(X_{n+1}|\mathcal{F}_{n}^{0})=\mathbb{E}(X_{n+1}|\sigma(X_{1},\dots,X_{n}))= \mathbb{E}(X_{n+1}) = 0\quad\text{g.s.}
za svaki n\ge0, pri čemu predzadnja jednakost slijedi zbog nezavisnosti niza (X_{n})_{n}.Dakle, X je niz martingalnih razlika koji je uz to i stacionaran Gaussovski slučajni proces budući da zbog nezavisnosti i normalnosti, za n\ge 0 vrijedi:
(X_{k},\dots,X_{k+n})\sim\mathbb{N}(\boldsymbol{\mu},\Sigma),\quad\forall k\ge 1,
\mathbb{\boldsymbol{\mu}}=(0,\dots,0), \Sigma=(\Sigma_{ij})_{ij}, \Sigma_{ij}=\text{Cov}(X_{i},X_{j}) = 0 za i\neq j te \Sigma_{ii}=\sigma^{2}.Neka je \sigma^{2} = 2. Generirat ćemo n = 100, 500 i 1000 slučajnih uzorka iz N(0,2) razdiobe duljine 100 te za svaki od njih odrediti vrijednost statistike S= \left(\sum_{k=1}^{n}X_{k}^{2}\right)^{-\frac{1}{2}}\sum_{k=1}^{n}X_{k}. Prema relaciji (
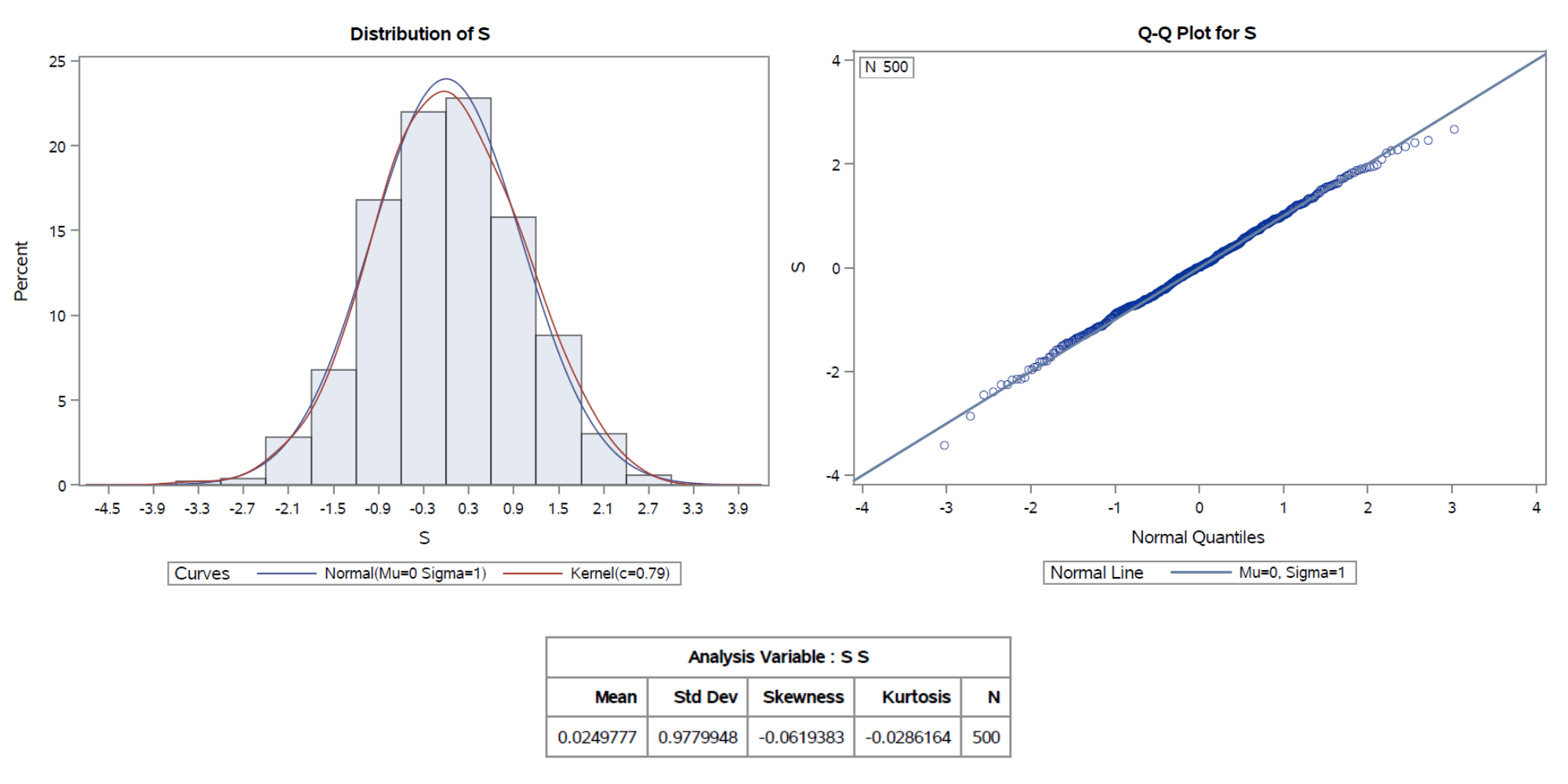
U prvom slučaju dobivamo uzorak (s_{n})_{n} duljine 100. P-vrijednost Kolmogorov - Smirnovljevog testa iznosi 0.8439, stoga zaključujemo da ne možemo odbaciti pretpostavku normalnosti promatranog uzorka. Na Slici 5 primjećujemo da oblik histograma dobro prati graf funkcije gustoće standardne normalne razdiobe, dok se točke na QQ-grafu relativno dobro grupiraju oko pravca, iako postoje odstupanja na rubovima. Premda primjećujemo prisutnost normalnosti u podacima, ta normalnost nije izrazito blizu idealne standardne normalne razdiobe. Nadalje, koeficijenti asimetrije i spljoštenosti su blizu nule, što dodatno sugerira da je ponašanje uzorka u velikoj mjeri normalno.

Slika 5: Histogram, QQ-graf, deskriptivne statističke mjere za n = 100.
Povećajmo sada broj generiranih uzoraka na 500 na način da prvih 100 uzoraka ostane isto kao ranije te se generira novih 400 uzoraka. Isti princip se primjenjuje u slučajevima s još većim brojem uzoraka.
Pogledajmo sada je li distribucija uzorka s_{1}, \dots, s_{500} nešto bliža nomalnoj distribuciji u odnosu na uzorak duljine 100.
U ovom slučaju je p-vrijednost Kolmogorov-Smirnovljevog testa 0.7156 pa ponovo ne odbacujemo pretpostavku normalnosti. Koeficijenti asimetrije i spljoštenosti su bliži nuli nego u prošlom slučaju, što sugerira nešto veću normalnost. To nam potvrđuje i izgled histograma i QQ-grafa prikazanih na Slici 6. Povećanjem broja generiranih uzoraka dobili smo distribuciju nešto bližu nomalnoj.
Slika 6:Histogram, QQ-graf, deskriptivne statističke mjere za n = 500.
Iz posljednjeg primjera vidimo da smo s povećanjem broja generiranih uzoraka dodatno poboljšali normalnost uzorka (s_{n})_{n}. P-vrijednost Kolmogorov-Smirnovljevog testa ostaje visoka i iznosi 0.9235, a koeficijenti asimetrije i spljoštenosti su još bliži koeficijentima standardne normalne razdiobe, dok izgled histograma i QQ-grafa ukazuje na još veću normalnost u podacima nego prije.
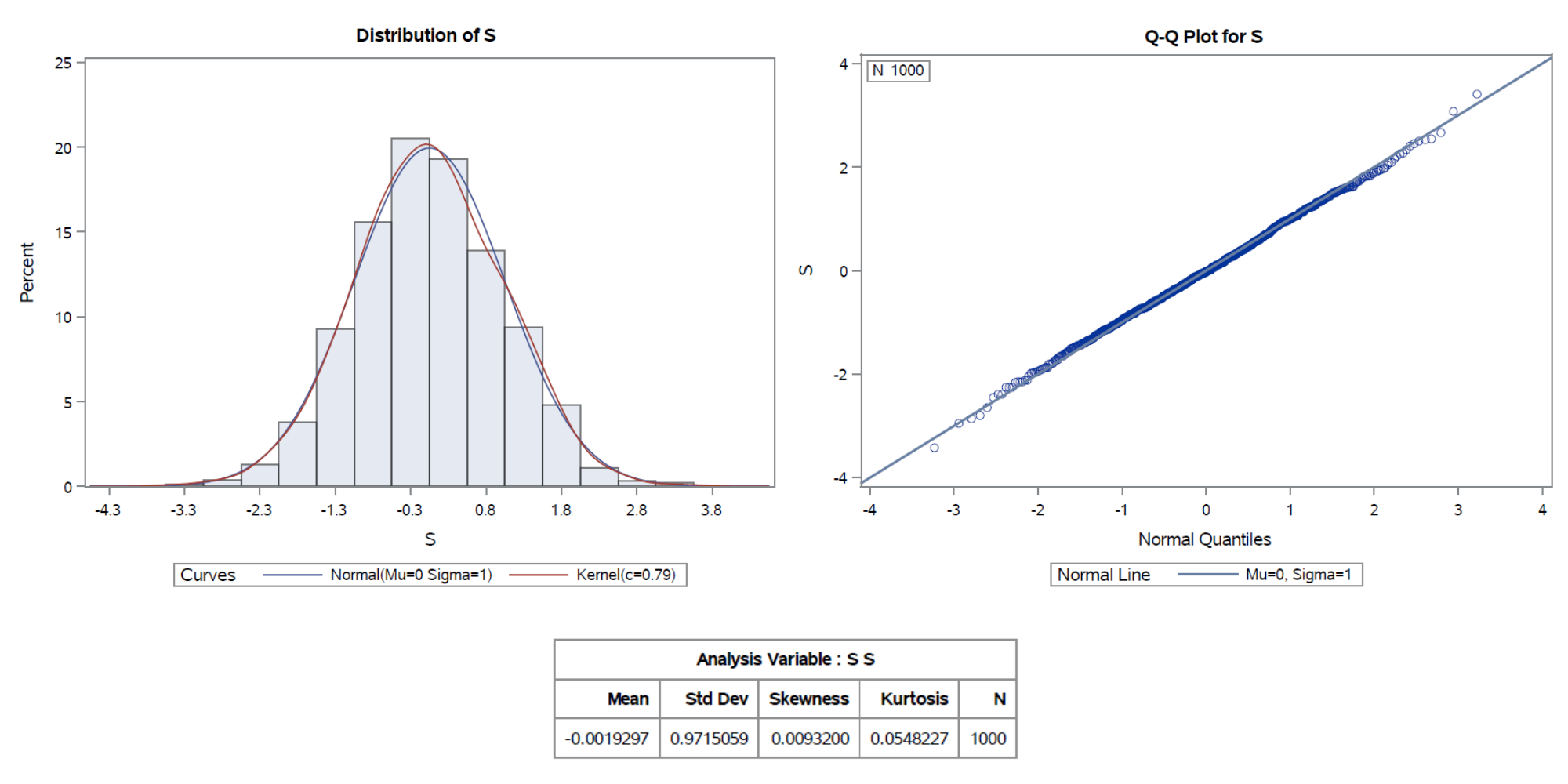
Slika 7:Histogram, QQ-graf, deskriptivne statističke mjere za n = 1000.
Dakle, primjećujemo da se rezultati poboljšavaju porastom broja generiranih uzoraka. Drugim riječima, u slučajevima s više podataka, distribucija djeluje bliža standardnoj normalnoj distribuciji u usporedbi s prethodnim situacijama, što je u skladu s očekivanjima temeljenima na relaciji (
\ \blacksquare
U zadnjem primjeru ćemo promatrati centralni granični teorem. Preciznije, pokazat ćemo da klasičan CGT vrijedi i u slučaju stabilne odnosno miješane konvergencije. Nadalje, vidjet ćemo da uz pomoć stabilne konvergencije možemo pokazati da postoji \lim_{n}\mathbb{P}(X_{n}\le Y) kada je Y prava slučajna varijabla, što iz konvergencije po distribuciji nije moguće dobiti, te ćemo pokazati čemu je taj limes jednak.
Primjer 3.6. (Klasični stabilni centralni granični teorem)
a) Neka je (Z_{n})_{n} niz nezavisnih realnih slučajnih varijabli na (\Omega,\mathcal{F},\mathbb{P}), (b_{n})_{n} niz u \mathbb{R}, (a_{n})_{n} niz pozitivnih realnih brojeva takav da a_{n}\rightarrow+\infty te X neka slučajna varijabla.
Definirajmo niz (X_{n})_{n} slučajnih varijabli s X_{n}:=\frac{1}{a_{n}}\left(\sum_{j=1}^{n} Z_{j}-b_{n}\right),\; n\in\mathbb{N}.
Pretpostavimo da vrijedi:
X_{n}\xrightarrow{d}X.
Pokažimo da tada vrijedi i
X_{n}\rightarrow X\;\text{miješano}.
Neka je \mathcal{G}=\sigma(Z_{n}:\:n\ge 1) i \mathcal{E}=\bigcup_{k=1}^{\infty}\sigma(Z_{1},\dots,Z_{k}). \mathcal{E} je algebra za koju vrijedi \sigma(\mathcal{E})=\mathcal{G}. Također, X_{n}\in\mathcal{G} za svaki n\in\mathbb{N}.
Neka je F\in\mathcal{E} proizvoljan takav da je \mathbb{P}(F)\gt 0. Tada postoji k\in\mathbb{N} takav da je F\in\sigma(Z_{1},\dots,Z_{k}).
Definirajmo niz slučajnih varijabli (Y_{n})_{n} s
Y_{n}:=\frac{1}{a_{n}}\left(\sum_{j=k+1}^{n} Z_{j} - b_{n}\right),\; n\gt k.
Vrijedi:
(17)
\begin{align} |X_{n}-Y_{n}|=\left|\frac{1}{a_{n}}\sum_{j=1}^{k} Z_{j}\right|\xrightarrow{n\rightarrow\infty}0\quad\text{na }\Omega. \end{align}
Nadalje, \sigma(Z_{1},\dots,Z_{k}) i \sigma(Z_{n}:\:n\ge k+1) su nezavisne \sigma-algebre, stoga je \mathbb{P}_{F}^{Y_{n}}=\mathbb{P}_{Y_{n}}.
Iz Y_{n}\xrightarrow{d} X slijedi \mathbb{P}_{Y_{n}}\xrightarrow{w}\mathbb{P}_{X}, a iz prethodne relacije \mathbb{P}_{F}^{Y_{n}}\xrightarrow{w}\mathbb{P}_{X}.
Jer je F\in\mathcal{E} bio proizvoljan, iz Teorema 2.5. (iii)\Rightarrow(i) slijedi Y_{n}\rightarrow X\;\mathcal{G}-miješano. Iz toga i (
X_{n}\rightarrow X\;\text{miješano}.
b) Neka je sada (Z_{n})_{n} niz nezavisnih jednako distribuiranih realnih slučajnih varijabli s očekivanjem \mu i varijancom \sigma^{2}\in (0,+\infty). Definirajmo niz slučajnih varijabli (X_{n})_{n} s
X_{n}:=\frac{1}{\sqrt{n}}\sum_{j=1}^{n}(Z_{j}-\mu),\:n\in\mathbb{N}.
Prema klasičnom CGT-u, vrijedi:
X_{n}\xrightarrow{d}N,
za N\sim N(0,\sigma^{2}). Ako s F_{N} označimo funkciju distribucije slučajne varijable N, tada gornju relaciju možemo zapisati na sljedeći način:
\lim_{n} \mathbb{P}(X_{n}\le x) = F_{N} (x),\;\forall x\in\mathbb{R}.
Dakle, za bilo koji realan broj x\in\mathbb{R}, niz (\mathbb{P}(X_{n}\le x))_{n} konvergira prema broju F_{N}(x). S druge strane, ako realan broj x zamijenimo slučajnom varijablom Y:\Omega\rightarrow \mathbb{R}, nije odmah jasno konvergira li niz (\mathbb{P}(X_{n}\le Y))_{n} i ako da, prema čemu. Odgovor na ovo pitanje dat će nam stabilna konvergencija.Uočimo, iz X_{n}\xrightarrow{d}N prema dijelu a) slijedi
X_{n}\rightarrow N\;\text{miješano}.
Neka je Y proizvoljna realna slučajna varijabla. Tada nam Teorem 2.5. daje
(X_{n},Y)\rightarrow(N,Y)\;\mathcal{G}\text{-stabilno},
iz čega slijedi
(18)
\begin{align} (X_{n},Y)\xrightarrow{d}(N,Y). \end{align}
\lim_{n}\mathbb{P}_{(X_{n},Y)}(D)=\mathbb{P}_{(N,Y)}(D).
Dakle, vrijedi
\begin{align*} \lim_{n} &\mathbb{P}(X_{n}\le Y) = \lim_{n} \mathbb{P}_{(X_{n},Y)}(D)=\mathbb{P}_{(N,Y)}(D) = \int \mathbb{P}_{N}(D_{y})\mathbb{P}_{Y}(dy) =\\ &=\iint\mathbb{1}_{D}(x,y)\mathbb{P}_{N}(dx)\mathbb{P}_{Y}(dy)=\int_{-\infty}^{+\infty}\int_{-\infty}^{y} \mathbb{P}_{N}(dx)\mathbb{P}_{Y}(dy) =\int_{-\infty}^{+\infty} \mathbb{P}_{N}((-\infty,y])d\mathbb{P}_{Y}(y), \end{align*}
pri čemu treća jednakost slijedi iz Fubinijevog teorema. Sada, uz funkciju distribucije F_{N(0,\sigma^{2})} normalne N(0,\sigma^{2}) razdiobe, gornji izraz konačno možemo zapisati kao
(19)
\begin{align} \lim_{n} \mathbb{P}(X_{n}\le Y)=\int_{-\infty}^{+\infty} F_{N(0,\sigma^{2})}(y) d\mathbb{P}_{Y}(y)=\int_{\Omega} F_{N(0,\sigma^{2})}(Y)d\mathbb{P} = \mathbb{E}\left(F_{N(0,\sigma^{2})}(Y)\right). \end{align}
\lim_{n} \mathbb{P}(X_{n}\le c)=F_{N(0,\sigma^{2})}(c),
što dobivamo i direktno iz klasičnog CGT-a.Primijetimo da ako u prethodnoj jednakosti konstantu c zamijenimo slučajnom varijablom Y te primijenimo matematičko očekivanje na slučajnu varijablu F_{N(0,\sigma^{2})}(Y) u limesu, dobivamo upravo dokazanu relaciju (
Primjerice, za niz \tilde{X}_{n}: = \frac{\overline{Z_{n}}-\mu}{\sigma}\sqrt{n},\:n\in N koji ima asimptotski normalnu N(0,1) razdiobu te slučajnu varijablu Y\sim N(0,1) nezavisnu od niza (\tilde{X}_{n})_{n}, intuitivno je jasno da bi vrijednost od \mathbb{P}(\tilde{X}_{n}\le Y) s porastom n-a trebala biti sve bliža \frac{1}{2} jer se za velike n niz (\tilde{X}_{n})_{n} ponaša po distribuciji sve sličnije slučajnoj varijabli Y. Uz prethodno dokazani rezultat sada se to lako i pokaže.
Naime, vrijedi F_{N(0,1)}(Y)=F_{Y}(Y)=U\sim U(0,1) pa iz (
\lim_{n} \mathbb{P}(\tilde{X}_{n}\le Y)=\mathbb{E}\left(F_{N(0,1)}(Y)\right)=\mathbb{E}\left(U \right)=\frac{1}{2}.
Bibliografija

