Niko Josipović Učenik III. razreda Tehničke škole Ruđera Boškovića

Marijana Krnić Profesorica matematike, izvrstan savjetnik u Tehničkoj školi Ruđera Boškovića

1UVOD

U matematici, kao i u mnogim drugim znanostima, pored osnovnih aritmetičkih operacija zbrajanja, oduzimanja, množenja i dijeljenja, često se susrećemo s operacijama potenciranja i korjenovanja. Primjerice, izračunavanje površine kvadrata s poznatom duljinom stranice zahtijeva kvadriranje te duljine. Međutim postavlja se pitanje: kolika je duljina stranice kvadrata ako je poznata njegova površina?

Ovakva vrsta pitanja uvodi nas u koncept kvadratnog korijena. No, kako uopće izračunati drugi korijen iz broja koji nije potpun kvadrat kao što su četiri ili devet?

U ovom radu ćemo prikazati metode korištene za približno računanje kvadratnog korijena, Babilonsku i Newtonovu metodu. Razmotrit ćemo i heuristički pristup problemu iz kojeg proizlazi nekoliko zanimljivih rezultata. Uz to, u radu su dane implementacije pojedinih postupaka u programskim jezicima C i Python.

2BABILONSKA METODA

Jedna od najranijih poznatih metoda za približno računanje kvadratnog korijena potječe iz vremena starog Babilona, zbog čega je poznata kao Babilonska metoda [4]. Riječ je o metodi koja za početnu vrijednost drugog korijena pozitivnog realnog broja a uzima neku pozitivnu vrijednost x_{0}, da bi se sljedeća, bolja aproksimacija x_{1} izračunavala kao aritmetička sredina brojeva x_{0} i \displaystyle \frac{a}{x_{0}}:

x_{1} = \frac{1}{2} \left( x_{0} + \frac{a}{x_{0}} \right).

Postupak nastavljamo induktivno pa formula općenito glasi:

(1)

x_{n+1} = \frac{1}{2} \left( x_{n} + \frac{a}{x_{n}} \right),

gdje n označava redni broj iteracije. Kako n teži u beskonačnost, vrijednost x_{n} se približava vrijednosti kvadratnog korijena broja a:

\lim_{{n \to \infty}} x_{n} = \!\sqrt{a}.

 

Slika 1: Prikaz približavanja aproksimacija Babilonske formule (1) kvadratnom korijenu

 

2.1NUMERIČKI PRIMJER

Svojstva Babilonske metode pokazat ćemo kroz sljedeći primjer. Pretpostavimo da tražimo vrijednost kvadratnog korijena broja dva, odnosno neka je a=2. Započinjemo s početnom vrijednošću x_{0}=5. Koristeći (1), dobivamo niz aproksimacija prikazanih u sljedećoj tablici (uz prikaz greške aproksimacija).

Tablica 1: Vrijednosti aproksimacija Babilonske formule

n	x_{n}	\lvert x_{n} - \sqrt{2} \rvert
0	5	3.586 \cdot 10^{0}
1	2.7	1.286 \cdot 10^{0}
2	1.72037	3.062 \cdot 10^{-1}
3	1.414215686275 \ldots	2.724 \cdot 10^{-2}
4	1.414213562375 \ldots	2.574 \cdot 10^{-4}
5	1.414213562373 \ldots	2.342 \cdot 10^{-8}

Uočavamo da je svaka sljedeća aproksimacija preciznija od prethodne. Također, promatrajući vrijednosti grešaka, primjećujemo kvadratnu konvergenciju, jer se svaka sljedeća greška smanjuje barem kvadratno u odnosu na prethodnu.
Prvo intuitivno objašnjenje učinkovitosti metode dao je Isaac Newton (1643. - 1727.), pokazujući da je to poseban slučaj Newtonove metode [3].
Program. Implementacija postupka približnog računanja kvadratnog korijena korištenjem Babilonske formule u programskom jeziku C može se pronaći u poglavlju Programi pod brojem 1.

Newtonova metoda ili metoda tangente predstavlja iterativni postupak koji se koristi za približno rješavanje nelinearnih jednadžbi. Postupak započinjemo početnom procjenom rješenja, a zatim se uzastopnim iteracijama postupno poboljšava. Njezina popularnost proizlazi iz učinkovitosti rješavanja jednadžbi za koje nemamo izravna rješenja, te brzine konvergencije [5].

Ideja Newtonove metode leži u upotrebi tangente kako bi aproksimirali nultočku neke funkcije [5]. Neka je f diferencijabilna funkcija definirana na intervalu I unutar kojeg postoji jedinstvena nultočka. Uz početnu pretpostavku x_{0} o rješenju, možemo odrediti tangentu na graf funkcije f u točki T_{0}(x_{0},f(x_{0})). Jednadžba te tangente je g(x)=f(x_{0} )+f'(x_{0})(x-x_{0}), a ideja je pronaći njenu nultočku x_{1}, uz uvjet da ona postoji. Uvjet da g ima nultočku je f'(x_{0} )\neq0 i f(x_{0} )\neq0, pri čemu drugi uvjet sugerira da smo već pronašli vrijednost funkcije koju tražimo. Ako u jednadžbu za tangentu (linearnu aproksimaciju) uvrstimo činjenicu da je g(x)=0, izraz za x_{1} glasi:

Ponavljajući induktivno ovaj postupak za svaku sljedeću aproksimaciju nultočke funkcije f dobivamo:

Neka je zadan pozitivan realan broj a. Cilj je pronaći x, takav da vrijedi x=\pm\sqrt{a}, odnosno x^{2}=a. Definirajmo funkciju f(x)=x^{2}-a. Primjećujemo da je problem određivanja kvadratnog korijena sveden na traženje nultočaka te funkcije. Budući da je ova funkcija diferencijabilna i ima jedinstveno pozitivno i negativno rješenje (nultočke su izolirane), možemo primijeniti Newtonovu metodu. Uvrštavanjem f(x)=x^{2}-a, te f'(x)=2\cdot x u (2), izvodimo formulu ekvivalentnu Babilonskoj (1):

Primjenom Newtonove metode došli smo do Babilonske formule i objašnjenja njene učinkovitosti. Međutim, za ovo objašnjenje potrebno je poznavanje infinitezimalnog računa, što Babiloncima nije bilo poznato [3]. Stoga ćemo do formule i objašnjenja doći na jednostavniji način.

Dan je izraz x^{2}=a. Transformacijom jednadžbe, izvodimo izraze za x:

Dakle, općenito pišemo:

Izveden općeniti izraz za x, (3), pripada klasi jednostavnih iteracija, jer je oblika

Tako smo problem rješavanja početne jednadžbe sveli na problem traženja fiksne točke1 funkcije \varphi(x). Da bismo ju pronašli, definiramo jednostavnu iteracijsku funkciju (4) za izraz (3):

Navedena iteracijska funkcija (5) može se, a i ne mora, približavati vrijednosti fiksne točke x, kako n teži k beskonačnosti, odnosno u ovom slučaju kvadratnom korijenu broja a. U svrhu pronalaženja izraza koji konvergiraju koristimo sljedeće teoreme:

Teorem 1. (Teorem o fiksnoj točki) Neka je \varphi\in C^{1}\left[a,b\right] za koju vrijedi:
1. \varphi\left(\left[a,b\right]\right)\subseteq[a,b]
2. i neka \exists\lambda\in\left[0,1\right\rangle, takav da je \lvert\varphi'(x)\rvert\leq\lambda,\forall x\in\left[a,b\right].
Tada x = \varphi(x) ima točno jedno rješenje \alpha na \left[a,b\right], te za proizvoljan x_{0}\in\left[a,b\right] i jednostavnu iteraciju x_{n+1}=\varphi(x_{n}),n\geq0 vrijedi

Teorem 2. Neka je \alpha rješenje jednostavne iteracije x = \varphi(x), \varphi neprekidno diferencijabilna na nekoj okolini od \alpha i \left| \varphi'(\alpha)\right| \lt 1. Tada vrijede svi rezultati Teorema 1, uz pretpostavku da je x_{0} dovoljno blizu \alpha.
Dokazi navedenih teorema mogu se pronaći u [1].

Kako je \varphi(x) = \displaystyle \frac{a+k\cdot x}{x+k}, njezina je derivacija \varphi'(x) = \displaystyle \frac{k^{2}-a}{(x+k)^{2}}. Također, poznata nam je jednakost \alpha=\!\sqrt{a}, pa prema Teoremu 2 gledamo kada vrijedi sljedeće:
[-15pt]

odnosno

Rješavanjem nejednadžbe, dolazimo do uvjeta koeficijenta k\gt 0, što znači da, ako iteracijska funkcija (5) zadovoljava taj uvjet, ona uspješno konvergira u okolini \! \sqrt{a}.
 

 

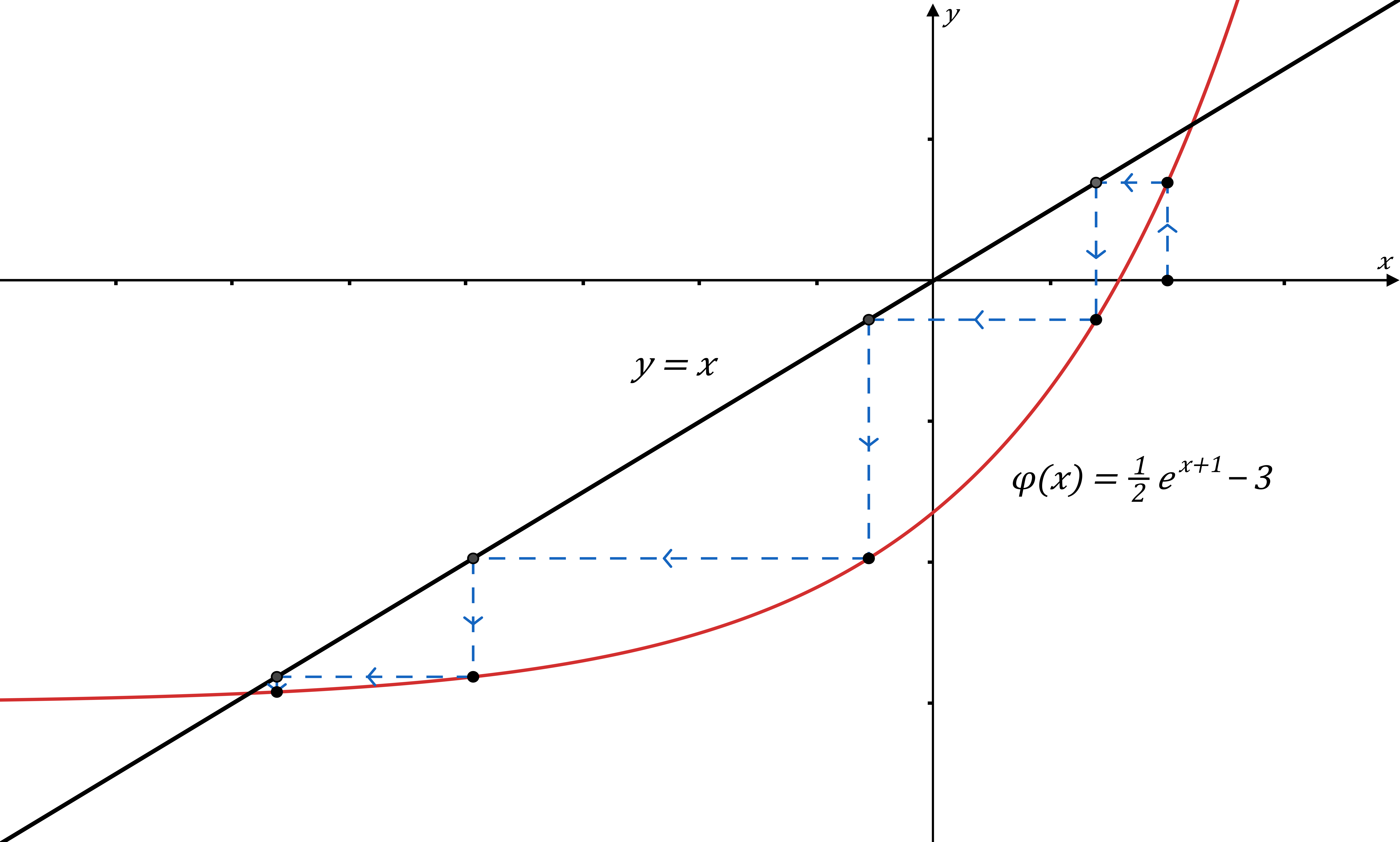
Primjena opće iteracijske funkcije (5) za približno računanje kvadratnog korijena broja a=2 pri različitim vrijednostima k\gt 0, dovodi do zanimljivog rezultata prikazanog na grafikonu 1.

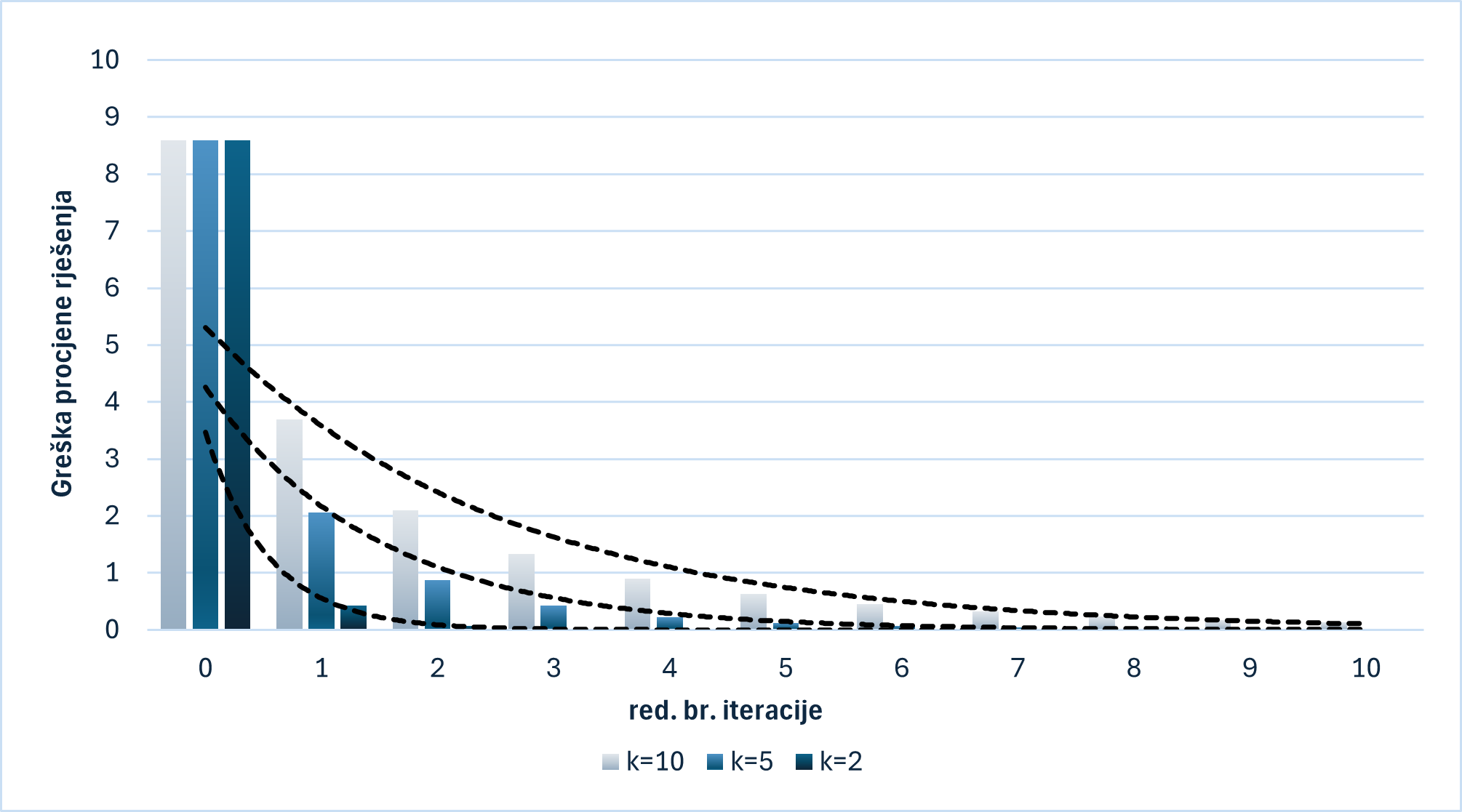
Uočavamo da pri različitim vrijednostima koeficijenta k dobivamo formule s različitim brzinama konvergencije. Pritom se nameće pitanje: koja vrijednost k daje najbržu konvergenciju?

S ciljem pronalaženja takvog k razmatramo slučaj, gdje je rezultat prve iteracije već konačan, odnosno x_{1}=\!\sqrt{a}, za bilo koju početnu vrijednost x_{0}. Uvrštavanjem u (5) dobivamo:

Izrazimo k iz prethodne formule:

Dobivamo da je za k=\!\sqrt{a} konvergencija najbrža. Stoga, izjednačimo k s aproksimacijom \!\sqrt{a}, odnosno s x. Uvrštavanjem u (5) izvodimo „dinamičku“ formulu (6), ekvivalentnu Babilonskoj. Dinamičku, jer je svaka sljedeća, bolja aproksimacija istovremeno nova vrijednost za k u idućoj iteraciji, čime uvjetujemo vrlo brzu konvergenciju formule

Program. Implementacija izračunavanja greške procjene rješenja pri različitim vrijednostima k i grafički prikaz tih rezultata u programskom jeziku Python prikazana je u poglavlju Programi pod br. 2.

Izjednačavanje k s x iznjedrilo je Babilonsku formulu, formulu vrlo brze konvergencije. To nas dovodi do idućeg pitanja: što ako za k uvrstimo bolju aproksimaciju od x, odnosno k izjednačimo s prethodno dobivenom formulom (6)

Uvrštavanjem u (5) dolazimo do nove, brže formule za približno računanje drugog korijena.

Postupak izjednačavanja k s novodobivenom formulom (isprva s x) i uvrštavanje u (5) rezultira sljedećim formulama:

Zanimljivo je kako formule imaju za jedan veći red konvergencije2 od prethodne. Kako bismo provjerili red konvergencije pojedine formule, koristimo Teorem 3.
Teorem 3. Neka je \alpha rješenje od x=\varphi(x) i neka je \varphip puta neprekidno diferencijabilna za sve x u okolini \alpha, za neki p\geq2. Nadalje, pretpostavimo da je

Ako je početna vrijednost x_{0} dovoljno blizu \alpha, iteracijska funkcija

imat će red konvergencije p.

U literaturi je prikazan i dokaz ovog teorema [1].

Tako primjerice, formule (6) i (7) korištenjem Teorema 3, u kojem razmatramo do kojeg p vrijedi niz jednakosti (8), imaju red konvergencije 2 i 3. Dolazak do toga jasno je prikazan u tablici 4.

Na temelju navedenog, postavljamo sljedeću hipotezu:

Hipoteza 1. Ponavljanjem opisanog postupka n puta dobiva se formula reda konvergencije n+1.

Da bismo dokazali istinitost hipoteze, analizirajmo formule dobivene opisanim postupkom, navedene u tablici 3. Uočavamo da su članovi brojnika svi neparni članovi razvoja \left(x_{n}+\!\sqrt{a}\right)^{m+1} u binomni red, što se može zapisat u obliku:

Slično tome, nazivnik čine svi parni članovi istog razvoja podijeljeni s \!\sqrt{a}, što može biti zapisano kao:

Iako su pravilnosti potvrđene samo za m\leq4, gdje je m\in\mathbb{N}, pretpostavit ćemo da one vrijede općenito, tj. za \forall m\in\mathbb{N}. Konačno, postupak svodimo na sljedeći izraz:

gdje izborom m konstruiramo formulu koju bismo dobili ponavljanjem postupka m puta.

Pretpostavka o općenitosti uočenih pravilnosti ne mora biti istinita. Stoga je potrebno dokazati da izraz (11) zaista konstruira formule na opisan način.

Dokaz. Dokaz ćemo provesti indukcijom.

Baza indukcije. Provjerimo da izraz (11) konstruira ispravnu formulu za m=1. Uvrštavanjem m=1 u (11) i sređivanjem dobivamo:

formulu ekvivalentnoj (6), što znači da je tvrdnja istinita za m=1. Pretpostavka indukcije. Pretpostavimo da za neki s\in\mathbb{N} vrijedi:

Korak indukcije. Pokažimo koristeći pretpostavku da vrijedi sljedeća jednakost:

Dobili smo jednakost (12), pa smo po principu potpune indukcije dokazali tvrdnju da izraz (11) konstruira formulu, za \forall m\in\mathbb{N}, koju bismo dobili ponavljanjem postupka m puta.

Izjednačimo izraz (11) s \varphi(x) i izračunajmo prvu derivaciju funkcije \varphi.

Funkcija \varphi(x) je glatka3, a njena prva derivacija u brojniku sadrži izraz \left(x-\!\sqrt{a}\right)^{m}. Dakle, niz jednakosti u (8) će zbog svojstva derivacije kompozicije i kvocijenta funkcije vrijediti zaključno s p=m+1. Time je Hipoteza 1 dokazana.

Na temelju prethodnog, moguće je konstruirati formule visokog reda konvergencije. Ipak, zbog velikog broja osnovnih aritmetičkih operacija (BOAO) po iteraciji, što je prikazano na grafikonu 2, takve se formule ne koriste.

 

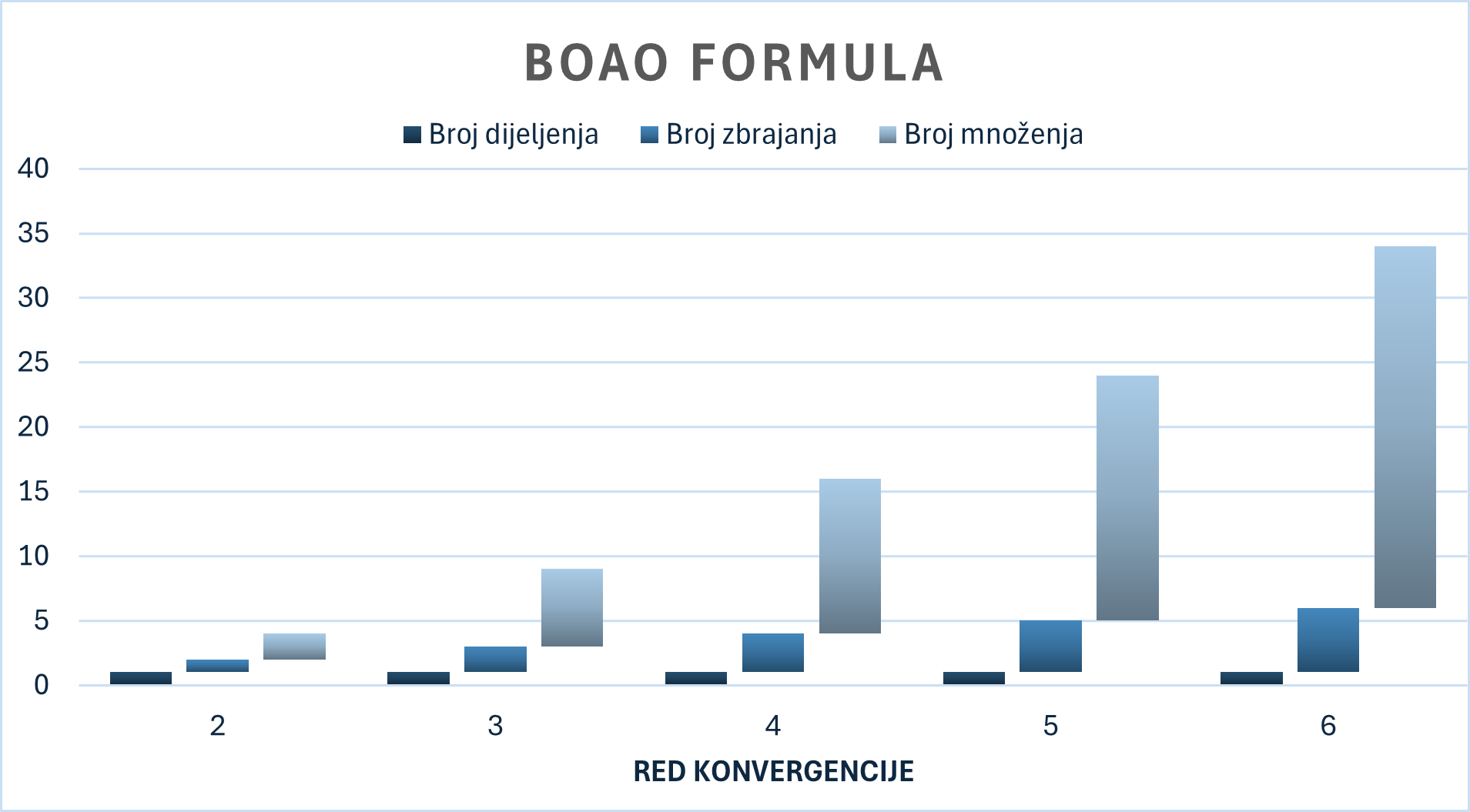
Kako bismo olakšali proces određivanja BOAO pojedine formule, implementirat ćemo ga u programski jezik C. Za to je potrebno izraz (11) pretvoriti u sumu koristeći binomnu formulu, što ćemo učiniti posebno za brojnik (9) i nazivnik (10):

Uvrštavanjem dobivamo izvedenicu izraza (11) koja glasi:

Spomenuti program nalazi se u poglavlju Programi pod br. 3, a prilikom korištenja uočavamo pravilnost prikazanu u tablici 5.

Uočavamo da niz vrijednosti promjena promjene oscilira, tako da za parne m iznosi 1, a neparne iznosi 2 (isključeno m=1). Pod pretpostavkom općenitosti, dokažimo da broj operacija za neki m\in\mathbb{N} u oznaci S(m) opisujemo formulom:
 

Vrijedi da zbrajanje promjene broja operacija do m (uključujući i m) iznosi S(m):

Opći član niza promjene broja operacija e_{m} računamo zbrajanjem prvog člana e_{1} = 4, s nizom promjena promjene do m (uključujući i m). Zbog pravilnosti niza, vrijedi formula:

gdje d_{1} označava broj parnih, a d_{2} broj neparnih brojeva u intervalu [2, m]. Izrazimo d_{1, 2} preko m:

Uvrštavanjem izraza za e_{m} u (15) dobivamo jednakost:

Dokaz. Dokazivanjem ove jednakosti indukcijom, dokazujemo ispravnost formule (14).
Baza indukcije. Provjerimo da jednakost (16) vrijedi za m=1.
Uvrštavanjem m=1 u (16) dobiva se 4 = 4, što znači da vrijedi za m=1.

Pretpostavka indukcije. Pretpostavimo da za neki s\in\mathbb{N} vrijedi:

Korak indukcije. Pokažimo da vrijedi i sljedeća jednakost:

Iz pretpostavke (17) slijedi:

Na osnovu definicija funkcija pod \left\lfloor\cdot\right\rfloor i strop \left\lceil\cdot\right\rceil za n\in\mathbb{Z} mogu se dokazati jednakosti:

Primijenimo li ih na izraz (18) dobivamo:

Dobivenom jednakosti, po principu potpune indukcije, formula (14) vrijedi za sve m\in\mathbb{N}, uz pretpostavku o općenitosti osciliranja vrijednosti niza promjena promjene.

Program. Koristeći formulu (14), program 3 može se zapisati u skraćenom obliku, dostupan u poglavlju Programi pod br. 4.

Dokazali smo ispravnost izraza (11) te pokazali jednu njegovu izvedenicu, (13), nastalu proširivanjem izraza u sumu. Za kraj ćemo spomenuti još jednu izvedenicu koja proizlazi iz sljedeće jednakosti, pri čemu su n i k prirodni brojevi:
 

Zamjenom odgovarajućih izraza u (13) dolazimo do spomenute izvedenice:

Zaključno, ovim radom smo istaknuli važnost različitih pristupa matematičkim problemima. Konkretno, istraživanjem drugačijeg pristupa problemu računanja kvadratnog korijena došli smo do nekoliko zanimljivih rezultata, kao što su:

Ovim rezultatima također potvrđujemo uspješnost pristupa i provedenog istraživanja. Daljnje istraživanje moglo bi uključivati primjenu ovog pristupa na računanje bilo kojeg n-tog korijena, te općenito primjenu pri rješavanju jednadžbi čija su rješenja usko povezana s operacijom korijena.

\clearpage

U ovoj točki prikazani su programski kodovi koji implementiraju postupke korištene u radu. Programi su napisani u programskim jezicima C (programi 1, 3 i 4) i Python (program 2). Njihova je svrha pokazati mogućnost implementacije postupaka na razumljiv i jednostavan način, a ne prikazati optimalan način njihove implementacije.