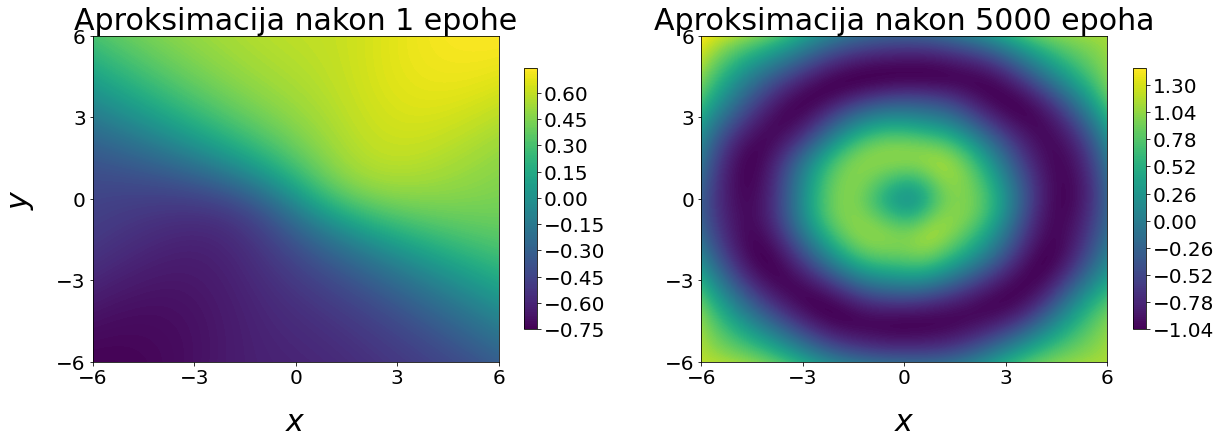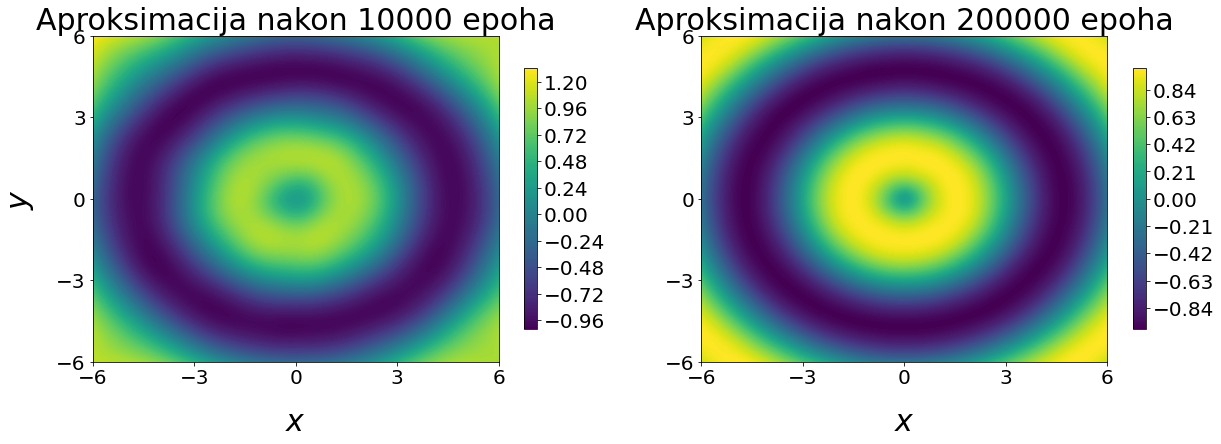Ključne riječi: neuronske mreže, Tensorflow 2, aproksimacija funkcija, Python 3

Znanstvenici i izumitelji žele kreirati strojeve sa sposobnošću razmišljanja barem od vremena stare Grčke, čemu svjedoče i mitološke priče. Također, stotinu godina prije izlaska prvog računala, ljudi su razmatrali mogućnost da stroj postane inteligentan. U početnoj fazi nastajanja umjetne inteligencije, područje se najprije dotaklo i riješilo neke vrlo zahtjevne i teške zadatake za ljude, ali jednostavne za računala zbog postojanja strogih formalnih pravila koja opisuju takve probleme, npr. igranje šaha. IBM-ov Deep Blue sustav za igranje šaha pobijedio je Garryja Kasparova, tada svjetskog prvaka u šahu, 1997. godine. Šah je vrlo kompleksna igra iz pogleda čovjeka, ali s obzirom da se može opisati vrlo formalnim algoritmom i pravilima, računalo može igrati šah s lakoćom, predviđajući veliki broj poteza unaprijed. Zanimljivo je da unotač tome, mnoge stvari koje su ljudima jednostavne, računalnim sustavima su izrazito teške, poput prepoznavanja objekata ili glasa [2].

Umjetna inteligencija (UI) postaje neizostavni dio naše svakodnevnice. Osim navedenih funkcija na pametnim telefonima, te igranja igara, tu su pametni satovi koji koriste UI za praćenje zdravstvenih parametara, poput otkucaja srca i kvalitete sna, pružajući korisnicima uvid u njihovo zdravlje u stvarnom vremenu. UI igra ključnu ulogu u modernoj upotrebi Interneta i e-mail komunikacije, gdje se koristi za filtriranje neželjene pošte, personalizaciju sadržaja i poboljšanje sigurnosti. U automobilskoj industriji doprinosi razvoju autonomnih vozila, poboljšava sustave pomoći vozačima i optimizira upravljanje prometom. U području medicine pomaže u dijagnostici, liječenju i upravljanju zdravstvenim informacijama. Pronalazi široku primjenu u gotovo svakom industrijskom sektoru, gdje značajno doprinosi efikasnosti, razvoju inovacija i automatizaciji procesa rada.

Zamislimo neki objekt koji nam je svima poznat, npr. stolica, i pokušajte si zamisliti u kojim se sve varijantama pojavljuje. Dakle, čovjek je izložen velikom broju informacija iz svijeta koji nas okružuje, čime konstantno dobiva iskustvo i nova znanja. Čovjek ima sposobnost razmišljati subjektivno i intuitivno, u situacijama kada je pojavu ili objekt gotovo nemoguće opisati na formalan način. Brojni dosadašnji pokušaji da se svijet oko nas opiše strogo formalnim jezikom kako bi računalni sustav mogao u njemu biti uspješan nisu dali zadovoljavajuće rezultate. Računalni sustavi iz područja umjetne inteligencije najčešće su sposobni raditi jednu ili nekoliko stvari vrlo dobro, ali zaostaju u implementaciji učenja iz iskustva koje dobivaju iz svijeta oko sebe. Razvoj velikih jezičnih modela, tzv. LLM (engl. Large Language Model) poput ChatGPT [7] i drugih, privukao je veliku pozornost javnosti na ubrzani razvoj umjetne inteligencije i stavlja naglasak na neka ključna pitanja za budućnost, poput sigurnosti i regulacijskih prava umjetne inteligencije. Takvi modeli daju dojam superiornosti nad čovjekom u nekim situacijama, iako se temelje na jednostavnom principu predviđanja, a trenirani su na ogromnim količinama podataka. Ovi sustavi primjer su začetka procesa dobivanja istinski inteligentnih sustava u budućnosti.

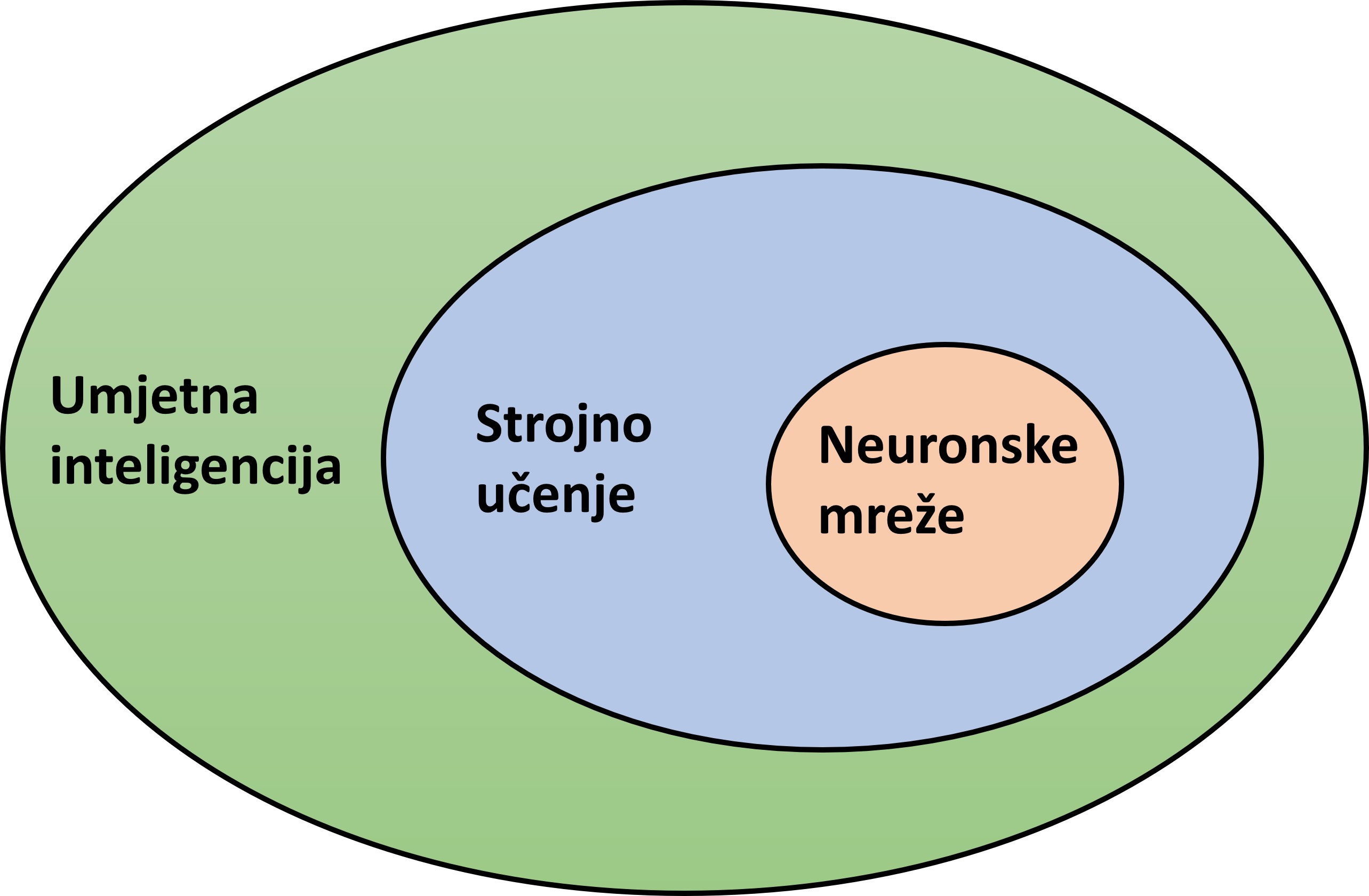
Dakle, umjetna inteligencija je računalni sustav koji može obavljati zadatke koji inače zahtijevaju ljudsku inteligenciju, kao što su vizualna percepcija, prepoznavanje govora, donošenje odluka i prevođenje s jednog jezika na drugi. Strojno učenje je grana umjetne inteligencije. Najvažnija značajka leži u sposobnosti učenja kada je izložena velikim količinama podataka, bez ljudske intervencije i programiranja. Učenje najčešće podrazumijeva da algoritmi strojnog učenja pokušavaju minimizirati zadanu pogrešku ili maksimizirati vjerojatnost točnog predviđanja. Obično su početna predviđanja pogrešna, stoga izmjerimo koliko su predviđanja pogrešna suprotstavljajući ih pravim ili očekivanim vrijednostima, a zatim upotrijebimo tu pogrešku da modificiramo sustav umjetne inteligencije. Neuronske mreže su alat strojnog učenja, a onda i umjetne inteligencije, što je ilustrirano na slici 1. Treniranje neuronskih mreža izvršava se na opisani način - nastavljamo mjeriti pogrešku i mijenjati parametre neuronske mreže sve dok ne postignemo dovoljno "malu" pogrešku. Više o tome može se pročitati u [4].

Slika 1: Hijerarhijski prikaz odnosa neuronskih mreža, strojnog učenja i umjetne inteligencije. Neuronske mreže su dio strojnog učenja, koji je dio umjetne inteligencije.

Neuronske mreže su računalni sustavi koji su inspirirani biološkim neuronskim mrežama koje čine životinjski mozak. Sastoje se od slojeva, a slojevi od neurona. Slojevi neuronske mreže su povezani jedni s drugima, te počinju ulaznim slojem koji prima podatke i šalje ih u skrivene slojeve. U skrivenim slojevima se podaci obrađuju i šalju u neurone izlaznog sloja koji daje izlaz neuronske mreže. Neka je N_{L} broj slojeva neuronske mreže. Ako je N_{L} \geq 3, pri čemu ulazni sloj ne ubrajamo, mrežu zovemo dubokom, a inače ju zovemo plitkom. Glavno obilježje neuronskih mreža je sposobnost učenja na temelju ulaznih podataka. Uobičajeno se većina skupa podataka koristi za učenje, dok se ostatak upotrebljava za testiranje sposobnosti generaliziranja - npr., 90% podataka koristi se za treniranje neuronske mreže, a preostalih 10% za testiranje. Jedan prolazak algoritma kroz podatke za treniranje (učenje) nazivamo epoha.

Neuronske mreže su iznimno prilagodljive, pomažu nam grupirati neobilježene podatke prema sličnosti na temelju ulaznih podataka, napraviti predviđanja i/ili klasificirati podatke na temelju skupa podataka za treniranje. Postoje brojne vrste neuronskih mreža, koje se razlikuju prema arhitekturi, načinu učenja i sl. Najčešće vrste neuronskih mreža su umjetne, povratne i konvolucijske. Princip učenja zasniva im se na sličnim matematičkim načelima. Imaju ulaze na temelju kojih kroz slojeve trebaju stvoriti smisleni izlaz koji su "naučile" minimizirajući funkciju gubitka. Svaki neuron posjeduje težinu w koja se propagira na sljedeći sloj kroz aktivacijsku funkciju i na taj način se dobivaju izlazi. Detaljnije o tome može se pronaći na web stranicama [5] i [6]. Na slici 2 prikazana je arhitektura neuronske mreže sa tri ulazna podatka, jednim skrivenim slojem koji sadrži četiri neurona i dva izlaza.

Slika 2: Grafički prikaz umjetne neuronske mreže koja sadrži ulazni, jedan skriveni i izlazni sloj.

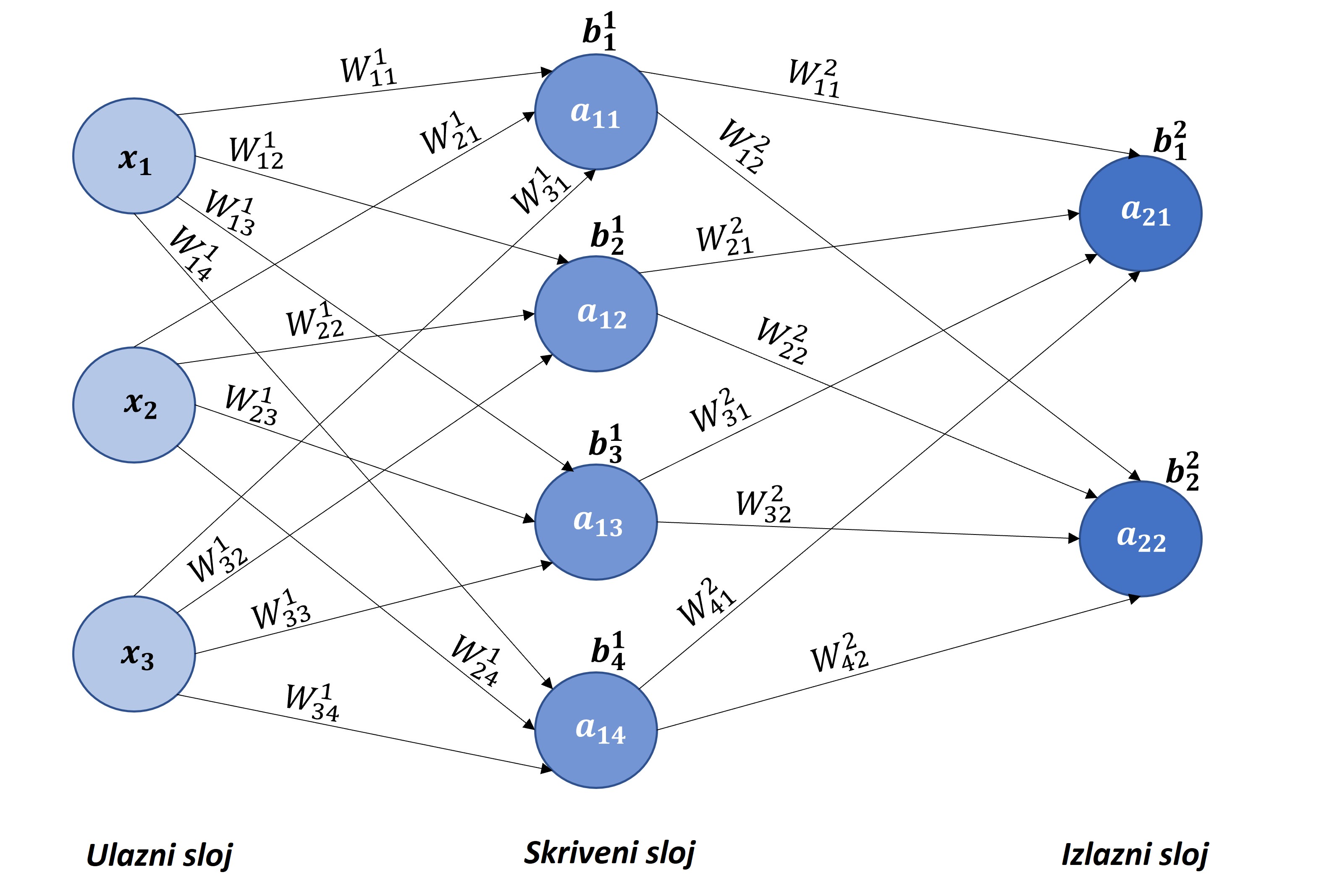
Ulazi imaju oznake x_{p}, p= 1, ..., n, težine W_{ij}^{k} \in \mathbb{R}, gdje je i redni broj neurona prethodnog sloja, j redni broj neurona trenutnog sloja, k redni broj trenutnog sloja, b_{j}^{k} \in \mathbb{R}, a vrijednost izraza a_{kj} se dobiva po formuli:

Funkcija \sigma se naziva aktivacijska funkcija i koristi se kako bi neuronska mreža mogla uspješno učiti nelinearna preslikavanja. Aktivacijska funkcija djeluje po komponentama ulaznog vektora. Izbor te funkcije vrlo je važan dio konstruiranja neuronske mreže, jer o njenom odabiru ovisi brzina učenja i performanse same neuronske mreže. Najčešće upotrebljavane aktivacijske funkcije su: sigmoid \sigma (x)= \frac{1}{1+e^{-x}}, tangens hiperbolni \sigma (x)= tanh(x), ReLU \sigma (x)= max(0,x) i Leaky ReLU \sigma (x)= max(\alpha x,x), gdje je \alpha\in \mathbb{R} najčešće pozitivna konstanta manja od jedan. Dublje mreže zapisujemo kao kompoziciju funkcija, te se tada za y \in \mathbb{R}^{d} neuronska mreža zapisuje kao kompozicija

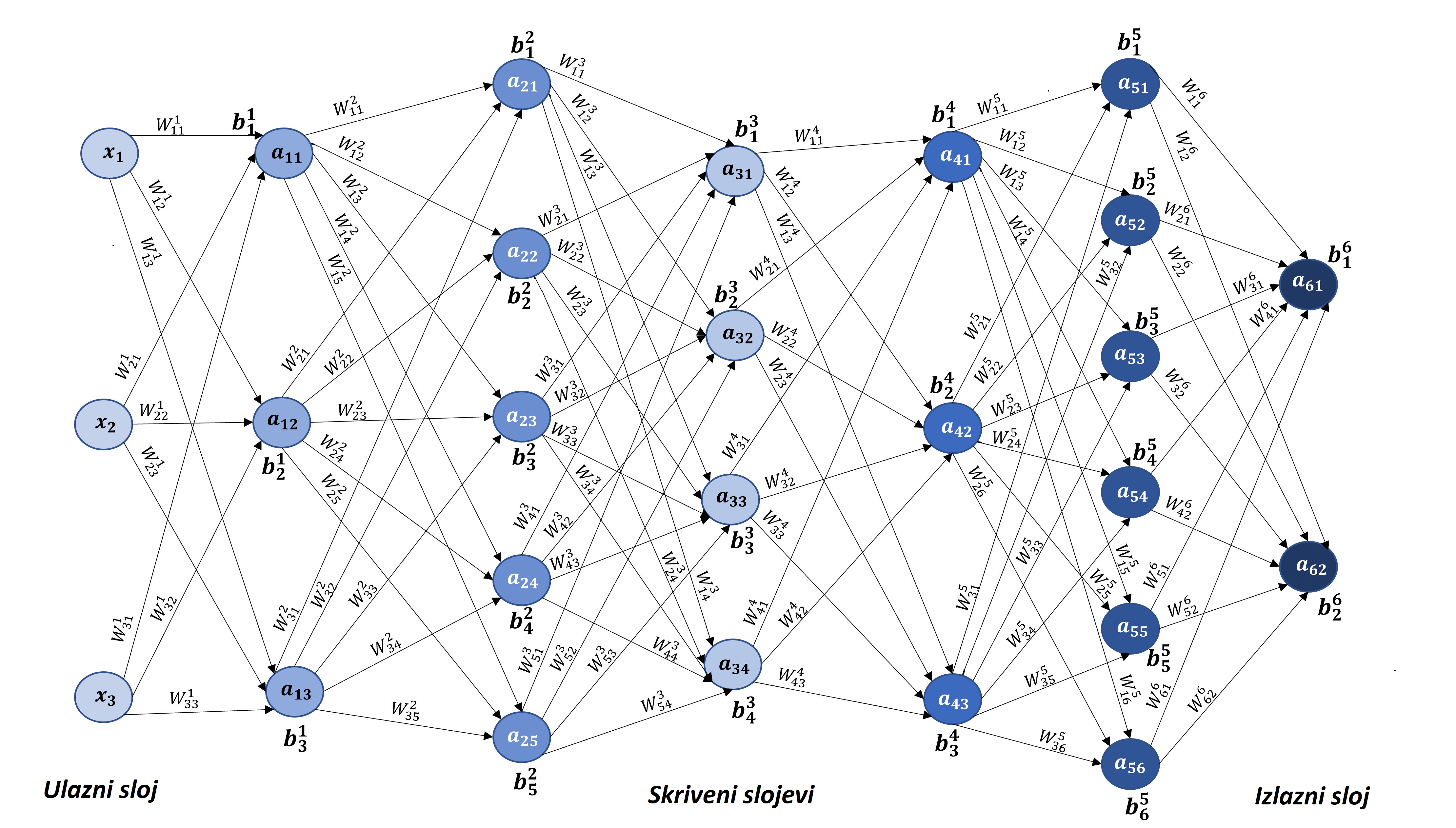
pri čemu je za 1 \le k \le K, C_{k}(z_{k})=W_{k} z_{k} + b_{k}, W_{k} \in \mathbb{R}^{d_{k+1} \times d_{k}}, z_{k} \in \mathbb{R}^{d_{k}}, b_{k} \in \mathbb{R}^{d_{k+1}}. Grafički prikaz neuronske mreže koja sadrži pet skrivenih slojeva dan je na slici 3.

Slika 3: Grafički prikaz umjetne neuronske mreže sa pet skrivenih slojeva.

Broj parametara za treniranje se računa po pravilu

gdje je L broj slojeva neuronske mreže, N_{k} broj neurona u k-tom sloju. Tada neuronska mreža sa slike 3. sadrži:

Ukupno, navedena arhitektura neuronske mreže sadrži 109 parametara za treniranje.

Univerzalni teorem aproksimacije implicira da su neuronske mreže univerzalni aproksimatori, odnosno da je bilo koju neprekidnu funkciju moguće aproksimirati neuronskom mrežom proizvoljno točno, uz određene uvjete. Teorem daje garanciju da takva neuronska mreža postoji, ali ne puno više od toga, odnosno ne daje informacije o odabiru hiperparametara neuronske mreže.

Dvije najraširenije vrste strojnog učenja su nadzirano učenje i nenadzirano učenje. U nadziranom učenju poznati su ulazni i očekivani izlazni podaci, dok kod nenadziranog učenja poznati su samo ulazni podaci. Za učenje neuronske mreže potrebno je odabrati jedan od optimizacijskih algoritama za učenje poput stohastičkog gradijentnog spusta, Adagrada, Adadelta, Adam, Nadam, RMSprop, AdaMax i slično. Funkcija koja računa pogrešku između željenih i dobivenih izlaznih vrijednosti naziva se funkcija gubitka. Funkcija gubitka definira se izrazom:

gdje \hat{y} predstavlja izlaz neuronske mreže, y je prava vrijednost, a \mathcal{L} je funkcija koji mjeri pogrešku na jednom primjeru trening skupa. Dakle, funkcija gubitka mjeri pogrešku neuronske mreže na skupu podataka za treniranje. Najčešći primjeri funkcija za mjerenje pogreške su prosječna kvadratna pogreška MSE= \frac{1}{n} \sum_{i=1}^{n} (\hat{y_{i}} - y_{i})^{2}, prosječna apsolutna pogreška MAE=\frac{1}{n} \sum_{i=1}^{n} |\hat{y_{i}} - y_{i}| i prosječna apsolutna postotna pogreška MAPE=\frac{100\% }{n} \sum_{i=1}^{n} \frac{|\hat{y_{i}} - y_{i}|}{|y_{i}|}.

Gradijent je vektorsko polje čije su komponente parcijalne derivacije funkcije. Gradijent određuje nagib tangente grafa funkcije, odnosno gradijent pokazuje smjer gdje je najveće povećanje funkcije. Gradijent mjeri koliko se izlaz funkcije promijeni ako se malo promjene ulazi. Nakon izračunate funkcije gubitka, računamo gradijent funkcije gubitka s obzirom na svaki parametar neuronske mreže. U neuronskim mrežama gradijent nam pomaže odrediti smjer i veličinu u kojemu trebamo mijenjati svaki parametar neuronske mreže kako bismo dostigli minimum funkcije gubitka. Kada neuronskoj mreži predajemo podatke u ulazni sloj koji se tada unaprijed šalju u skrivene slojeve sve do izlaznog sloja nazivamo forward propagation. Tijekom treniranja pomoću forward propagation računamo vrijednost funkcije gubitka. Back propagation (BP) algoritam informaciju o vrijednosti funkcije gubitka šalje od izlaznog sloja unazad sve do ulaznog sloja kako bi izračunao gradijent funkcije gubitka u odnosu na svaki parametar neuronske mreže, koristeći pravilo derivacije složene funkcije. Prema tom pravilu računa gradijent funkcije gubitka u odnosu na svaki parametar, računajući gradijent jedan po jedan sloj, ponavljajući unatrag od izlaznog sloja kako bi se izbjeglo suvišno izračunavanje međučlanova. Više se može pronaći u [2]. BP uključuje optimizaciju pogreške koristeći deterministički algoritam gradijentnog spusta. Glavni nedostatak BP algoritma je problem čestog pronalaženja lokalnog umjesto globalnog minimuma funkcije gubitka, stoga je moguće unaprijeđivanje nekim drugim determinističkim (npr. metoda drugoga reda) ili stohastičkim metodama.

Metoda stohastičkog gradijentnog spusta pomoću funkcije gubitka i gradijenta uči neuronsku mrežu traženo preslikavanje. Ona je iterativni algoritam za traženje točke lokalnog minimuma neprekidno diferencijabilne funkcije f: \mathbb{R}^{n} \rightarrow \mathbb{R} i oblika je:

gdje je x^{(0)} početna aproksimacija, \alpha_{k} \gt 0 duljina koraka u smjeru vektora smjera kretanja p^{(k)}=-\nabla f(x^{(k)}), a \nabla f(x^{(k)}) gradijent funkcije f u točki x^{(k)}. Detaljnije o algoritmima se može pročitati u [2].

Stopa učenja je skalar koji će odrediti duljinu koraka prema minimumu funkcije. Taj parametar ne smije biti ni prevelik ni premalen za učenje neuronske mreže i ovisi o problemu koji se rješava. Ako je stopa učenja prevelika, algoritam će premašiti cilj i možda neće dosegnuti do minimuma, a ako je premala, proces učenja će trajati predugo.

Prilikom učenja neuronskih mreža često dolazi do problema overfita, odnosno prevelikog prilagođavanja trening skupu. Moguće je na trening skupu dobiti gotovo 100% točnost predviđanja, a na test skupu samo 60%, tj. kažemo da neuronska mreža nema dovoljno dobro svojstvo generalizacije. Problem overfita se nastoji ukloniti metodama regularizacije. Najčešće korištene su L_{1} i L_{2} regularizacija, dodavanje dropout slojeva i dodavanje regularizacijskog izraza na funkciju gubitka. U slučaju prevelikog broj parametara za učenje s obzirom na broj ulaznih podataka može doći do problema underfita, gdje neuronska mreža ne može učiti efikasno iz trening skupa niti na njemu samom. Tada je najčešće potrebno mijenjati arhitekturu neuronske mreže i/ili promijeniti skup ulaznih podataka.

Za numeričke eksperimente koristili smo Python 3 i prikladne pakete. Najvažniji korišteni paketi su Tensorflow 2 [1] , numpy, scipy, matplotlib i FEniCS [3], koji omogućavaju rad s neuronskim mrežama, vizualizaciju rezultata i njihovu analizu. Treniranje je vršeno na radnoj stanici AIME AI Workstation T502 koja sadrži grafičku karticu RTX 3080. Nekoliko skripti s numeričkim eksperimentima se nalaze na GitHub poveznici1 i mogu služiti za učenje rada s neuronskim mrežama u paketu Tensorflow 2, te tehnikama analize pogreške rješenja u području numeričke analize.

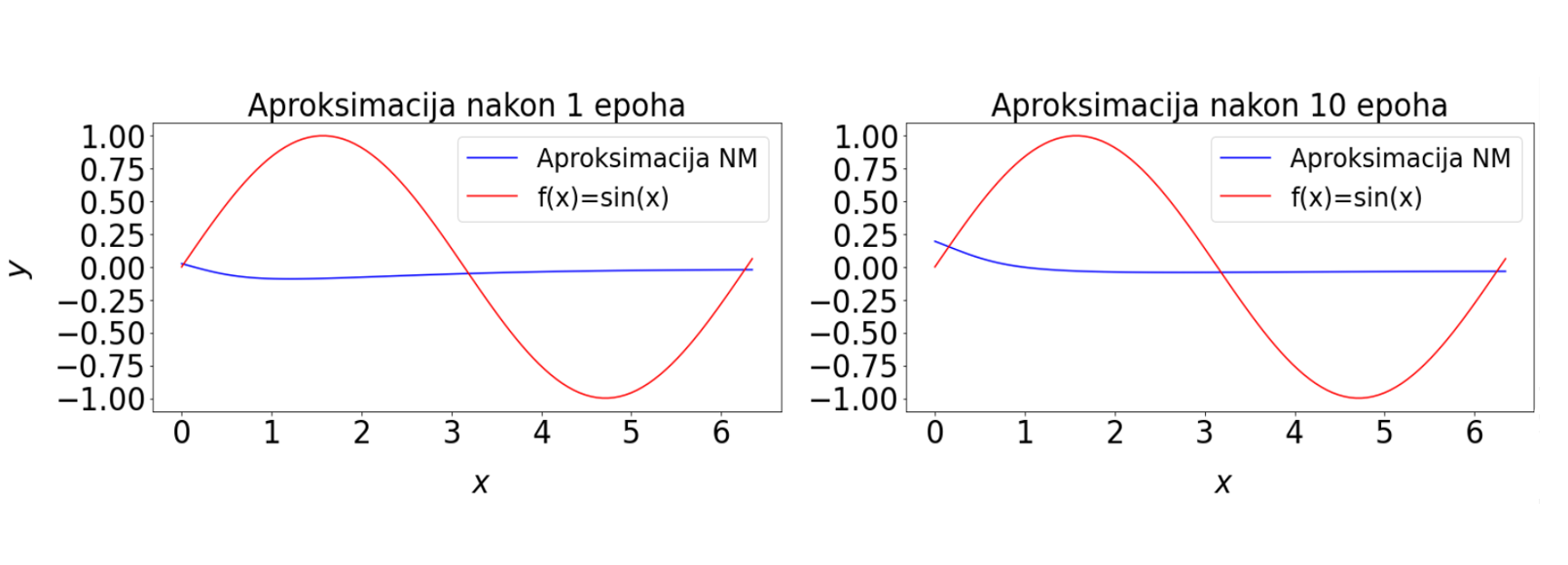
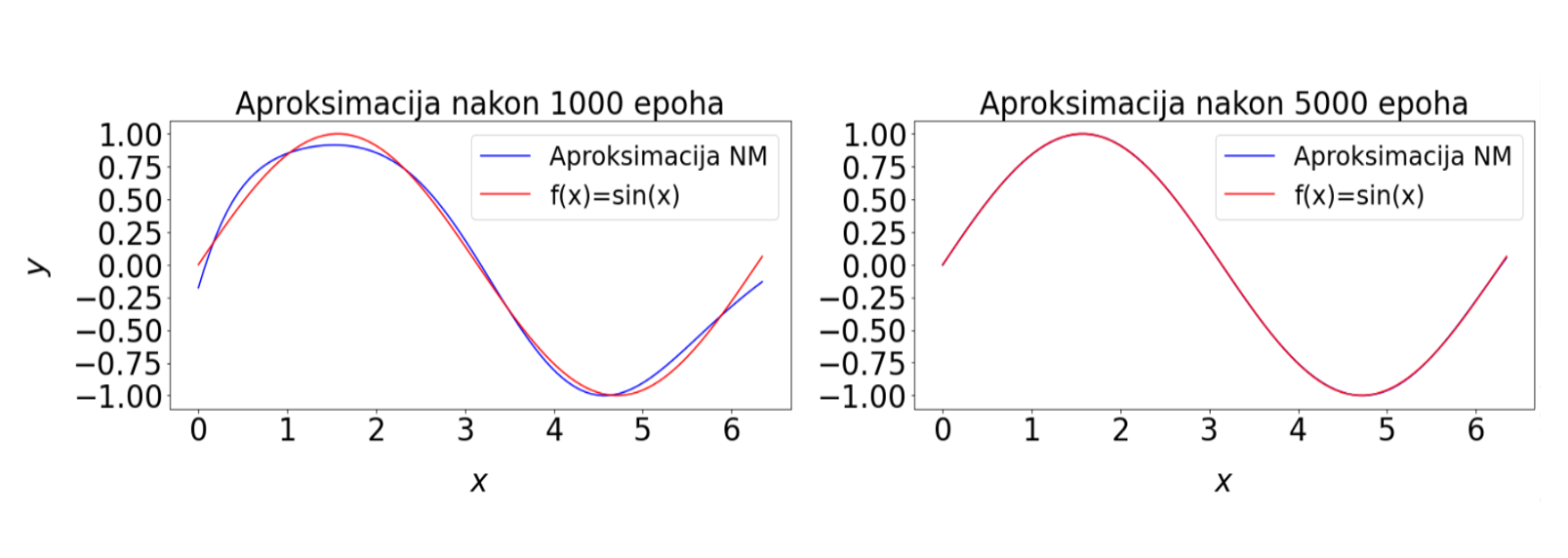
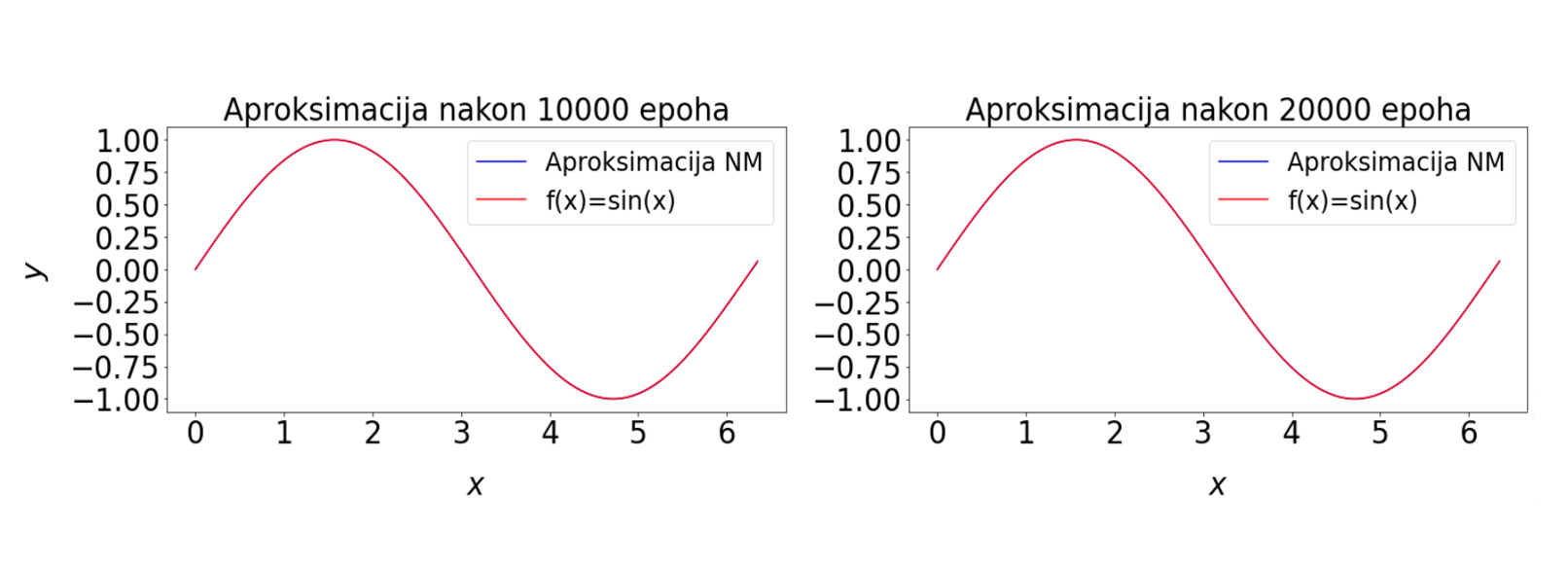
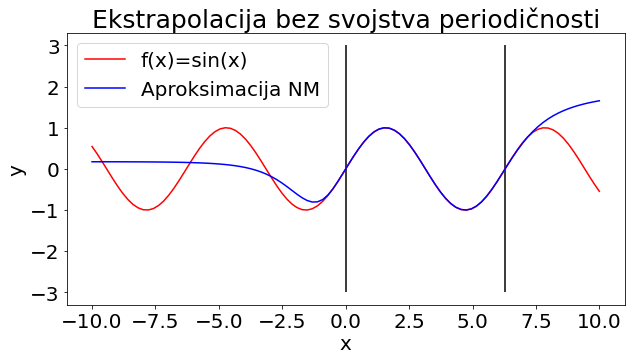
Prvi numerički eksperiment je periodička funkcija jedne varijable f(x) = \sin(x). Neuronsku mrežu ćemo trenirat na uniformnoj mreži čvorova osnovnog perioda, a analizirati rješenja na drugom skupu čvorova u osnovnom periodu, kao i problem ekstrapolacije. Također, izračunati ćemo relativnu pogrešku u L_{2} normi. Na slici 4. prikazan je primjer Tensorflow grafa arhitekture neuronske mreže.

Slika 4: Primjer arhitekture neuronske mreže koja osim ulaznog i izlaznog sloja sadrži pet skrivenih slojeva od kojih svaki sadrži 5 neurona. Ova arhitektura sadrži 136 parametara za treniranje.

U tablici 1. predstavljeni su rezultati testova prilikom treniranja neuronske mreže za funkciju f(x)=\sin(x). Za početak treniranja neuronske mreže definirat ćemo ulazne i izlazne podatke, domena ulaznih podataka će biti segment [0, 2\pi]. Stopa učenja za prvih 5000 epoha bit će 0.001, od 5000 epoha do 15000 epoha 0.0001, a od 15000 epoha do završetka treniranja 0.00005. Za optimizacijsku metodu koristimo Adam, a za funkciju gubitka MSE. Slovo u nazivu testa u prvom stupcu nam govori koju aktivacijsku funkciju smo koristili za treniranje neuronske mreže. Za slovo t je korištena aktivacijska funkcija \tanh, a za r je korištena aktivacijska funkcija RELU.

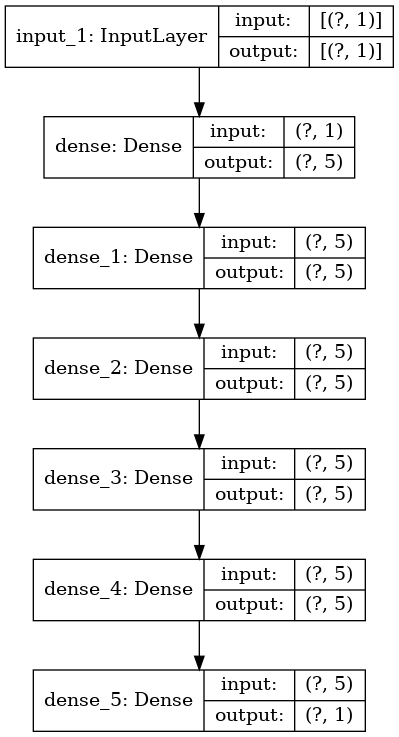
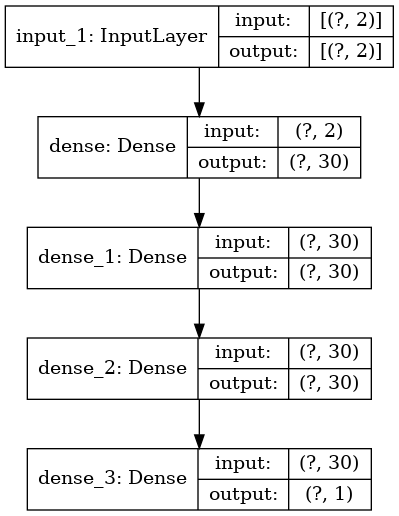
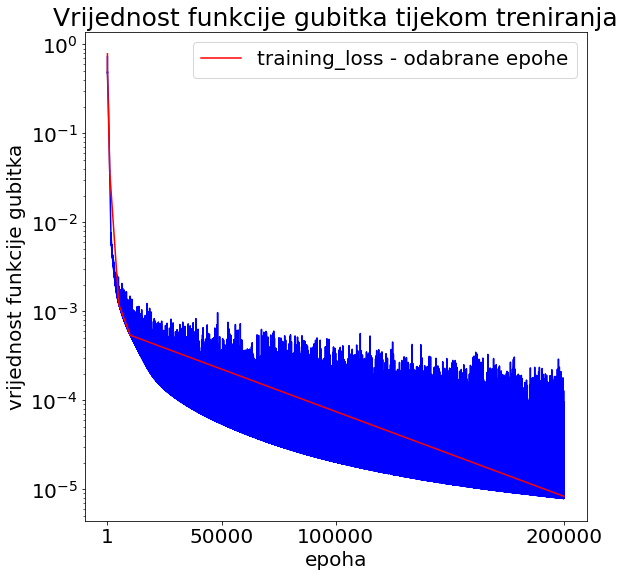
Naredna analiza, slike i grafovi odnositi će se na neuronsku mrežu testa t10 iz tablice čija je arhitektura prikazana na slici 4. Na grafu 6. prikazana je vrijednost funkcije gubitka po epohama. Vidljiv je efekt promjene stope učenja, koji omogućava daljnje smanjenje vrijednosti funkcije gubitka. Graf 7. prikazuje rezultat testa 1 - izvrednjavamo neuronsku mrežu u točkama koje nisu korištene prilikom treniranja i uspoređujemo rješenje s funkcijom sinus dobivenom u paketu numpy. Kako bismo pratili napredak neuronske mreže, na slici 5. prikazati ćemo za epohe 1, 10, 1000, 5000, 10000 i 20000 funkciju f(x)=\sin(x) i aproksimaciju neuronske mreže.

Slika 5: Aproksimacija funkcije f(x) tijekom treniranja i funkcija f(x)=\sin(x). Aproksimacija funkcije je sve bliža stvarnim vrijednostima funkcije f(x)=\sin(x) kako se povećava broj epoha.

Slika 6: Vrijednost funkcije gubitka tijekom treniranja funkcije jedne varijable. Plava krivulja prikazuje vrijednost funkcije gubitka po svim epohama, dok crvena u odabranim - epohama u kojima crtamo trenutne aproksimacije. Veće oscilacije vrijednosti funkcije gubitka ukazuju da je stopa učenja prevelika. Zato koristimo Keras callback metodu koja omogućava da se stopa učenja mijenja tijekom treniranja prema zadanim uvjetima.

Test 1


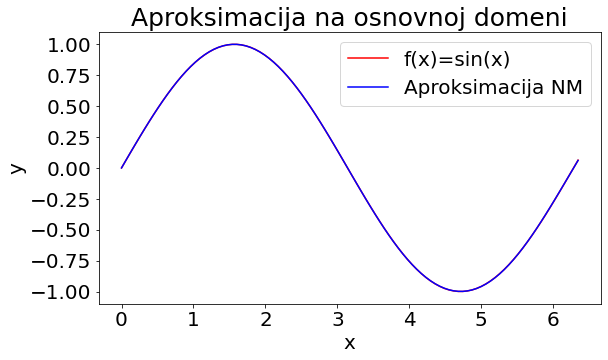
Provesti ćemo testiranje neuronske mreže na drugačijem skupu točaka od onih sa kojima je trenirala, ali su ulazni podaci iz iste domene. Računamo funkciju gubitka i uočavamo da je reda 10^{-7}, odnosno da je prosječna razlika između željenih i dobivenih izlaznih vrijednosti na razini jednostruke preciznosti realnih brojeva na računalu. Grafički prikaz na slici 7. dodatno potvrđuje da se funkcija f(x)=\sin(x) i funkcija koja predstavlja predviđanje neuronske mreže vizualno poklapaju. Konačnu provjeru radimo pomoću mjerenja relativne L_{2} pogreške koristeći Gaussovu integraciju. Računanjem po formuli E_{rel} =\sqrt{ \frac{\int_{\Omega} | u - \hat{u} |^{2}}{\int_{\Omega} |u|^{2}}} dobivamo da je pogreška jednaka 9.37\cdot 10^{-4}. Čvorove i težine za Gaussovu integraciju možemo dobiti korištenjem scipy paketa na intervalu (-1, 1), a zatim linearnom transformacijom dobivamo čvorove na željenom intervalu (a, b):

Formula Gausove integracije u jednoj dimenziji je dana izrazom:

Slika 7: Aproksimacija na osnovnoj domeni koristeći drugi skup točaka - test 1.

Test 2


U drugom testiranju neuronskoj mreži su dane različite točke od onih sa kojima je trenirala, ali i proširena domena ulaznih podataka na segment [-10,10]. Vrijednost funkcije gubitka sada iznosi 0.37, što je nekoliko redova veličine veće od rezultata na osnovnoj domeni. Analizom grafičkog prikaza 8, koji prikazuje rezultate drugog testa, može se uočiti da se funkcija f(x)=\sin(x) i funkcija koja predstavlja predviđanje neuronske mreže poklapaju na segmentu [0,2\pi] na kojem je neuronska mreža trenirala. Izvan intervala treninga navedene dvije funkcije su vrlo različite. Optimizacijska metoda se zasniva na gradijentu koji je lokalno svojstvo i zato izvan granica domene na kojoj je neuronska mreža trenirana, nema garancije da će aproksimacija biti točna.

Slika 8: Ekstrapolacija aproksimacije funkcije f(x) = \sin(x) bez svojstva periodičnosti na domenu [-10, 10].

Test 3


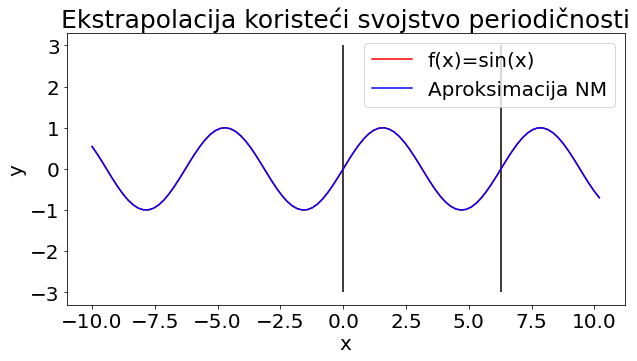
Pokušat ćemo popraviti rezultate prethodnog testa tako da ulazne podatke premjestimo u osnovni period, a zatim provodimo treće testiranje s novim ulaznim podacima. Za funkciju gubitka dobivamo vrijednost od 4.45\cdot 10^{-7}, što je veliko poboljšanje u odnosu na vrijednost funkcije gubitka iz drugog testiranja. Analizom grafičkog prikaza 9. moguće je uočiti da se sada funkcija f(x)=\sin(x) i funkcija koja predstavlja predviđanje neuronske mreže poklapaju na cijelom segmentu [-10,10], odnosno i na trening skupu i na test skupu. Iz toga se može zaključiti da se problem ekstrapolacije može uspješno riješiti koristeći svojstvo periodičnosti.

Slika 9: Ekstrapolacija aproksimacije funkcije f(x) = \sin(x) koristeći svojstvo periodičnost.

Dodatnu provjeru radimo izračunom relativne L_{2} pogreške na segmentu [-1000,1000]. Za pogrešku dobivamo vrijednost 9.38\cdot 10^{-4}, što je vrlo zadovoljavajući rezultat budući da smo značajno proširili segment na kojem računamo pogrešku u odnosu na segment na kojem je neuronska mreža trenirana.

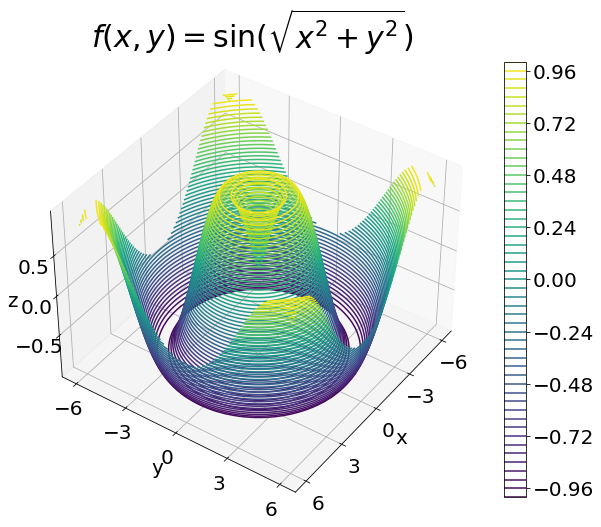
Testirat ćemo učenje neuronske mreže na primjeru funkcije s dvije varijable:

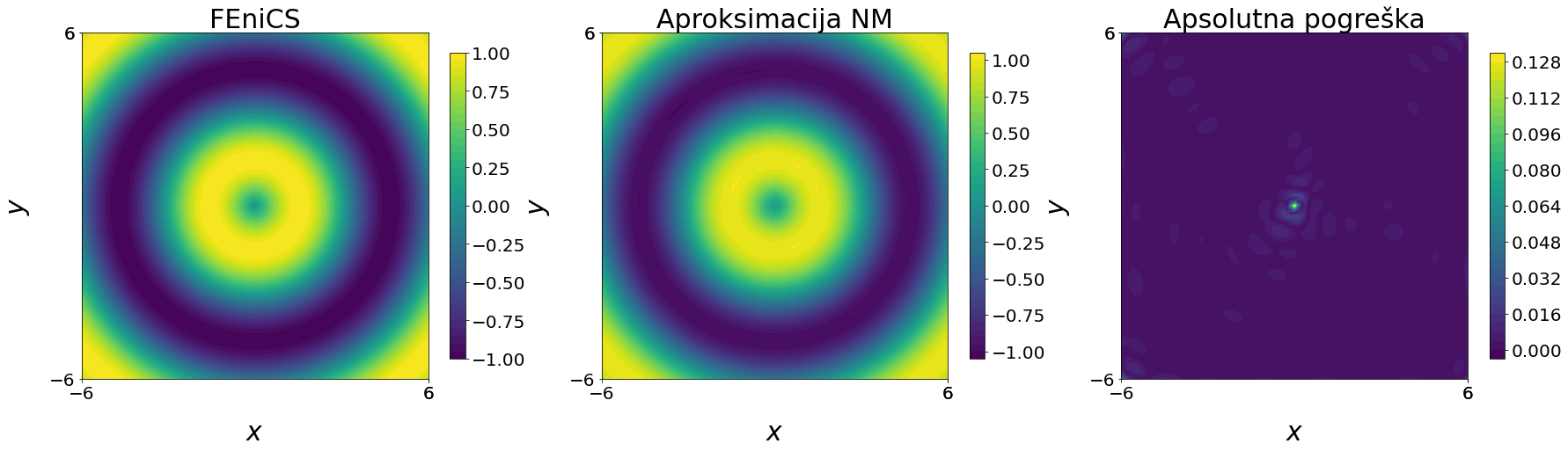
Za analizu i grafički prikaz dobivenih rješenja koristit ćemo paket FEniCS [3]. FEniCS paket sadrži funkcije koje nam omogućavaju jednostavno računanje relativne pogreške u L_{2} normi, što inače ne bi bilo jednostavno računati u dvije dimenzije.

Slika 10: Graf funkcije f(x, y) u 3D (lijevo) i pomoću paketa FEniCS (desno).

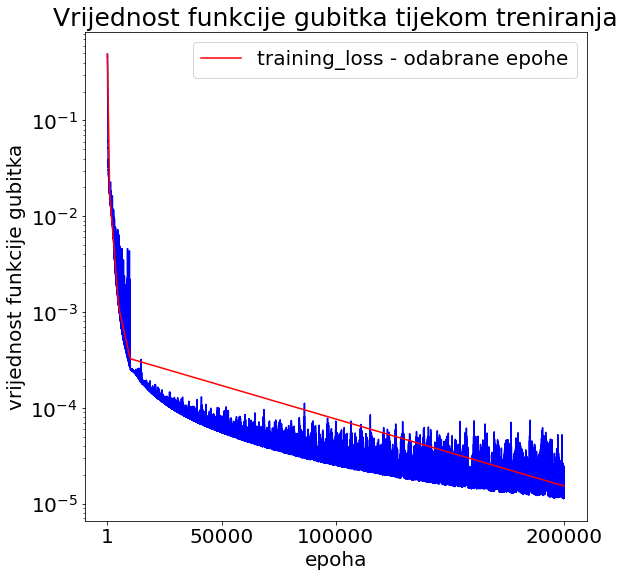
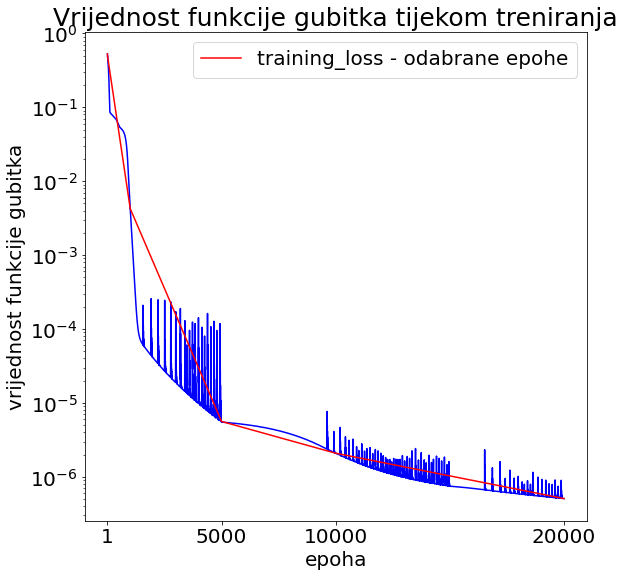
Ponovno ćemo testirati različite arhitekture i hiperparametre neuronske mreže i gledati funkciju gubitka, kao i relativnu pogrešku u L_{2} normi. Funkcija f(x, y) ima bogatu strukturu i promatrat ćemo aproksimaciju neuronskom mrežom kroz epohe treniranja. Čvorove i vrijednosti funkcije za treniranje generirat ćemo na uniformnoj mreži, a zatim će se za izračun relativne L_{2} norme koristiti čvorovi mesha FEniCS paketa - to je ujedno i test neuronske mreže koja ovdje treba aproksimirati funkciju f(x, y) u različitim točkama od onih u kojima je trenirala. Primjer Tensorflow grafa arhitekture neuronske mreže dan je na slici 11. Paket FEniCS koristi metodu konačnih elemenata, pa je potrebno generirati mesh - uzimamo 100 točaka po svakoj osi i koristimo P3 elemente za dobivanje rješenja visoke točnost. Ovakav mesh sadrži 90601 stupanj slobode.

Slika 11: Primjer arhitekture neuronske mreže koja sadrži tri skrivena sloja sa 30 neurona i izlaznim slojem koji ima jedan neuron. Ovakva arhitektura ima 1981 parametar za treniranje. Skraćeno, možemo ovu arhitekturu zapisati u obliku (2, 30, 30, 30, 1).

U tablici 2. prezentirani su rezultati treniranja neuronske mreže za danu funkciju f(x, y)=\sin\left(\sqrt{x^{2}+y^{2}}\right), x, y \in [-6, 6]. Za svaki eksperiment navedeni su važni hiperparametri kako je opisano u kazalu.

Na slici 12. vidljiv je efekt treniranja s i bez funkcije koja omogućava promjenu stope učenja tijekom treniranja. Smanjenje stope učenja tijekom treniranja često omogućava lakše približavanje minimumu funkcije gubitka. Na slici 13. vidljivo je poboljšanje aproksimacije željene funkcije neuronskom mrežom kroz epohe. Neuronska mreža i ovdje kreće od slučajnih vrijednosti i na početku nije nalik traženoj funkciji. Treniranjem neuronska mreža se približava željenoj funkciji. Dobiveno rješenje uspoređujemo s rješenjem dobivenim u paketu FEniCS-u. Na slici 14. prikazana su rješenja FEniCS paketa i aproksimacija rješenja neuronskom mrežom te apsolutna pogreška dobivena izrazom \vert u_{FEniCS} - u_{NN}\vert. Nadalje, izračunata je relativna pogreška aproksimacije neuronske mreže s obzirom na FEniCS rješenje koristeći funkciju errornorm paketa FEniCS. Iz tablice 2. vidljivo je da za brojne arhitekture možemo postići relativnu razliku reda 10^{-3}, što je zadovoljavajuće. Napomenimo da je rješenje u paketu FEniCS dobiveno koristeći 90601 stupanj slobode, dok neuronske mreže u eksperimentima sadrže značajno manji broj parametara.

Slika 12: Vrijednost funkcije gubitka tijekom treniranja bez callback funkcije za stopu učenja (lijevo) i s callback funkcijom za stopu učenja (desno).

Slika 13: Aproksimacija funkcije f(x, y) tijekom treniranja arhitekturom (2, 30, 30, 30, 1) i fiksnom stopom učenja 0.0005. Vidljivo je poboljšanje aproksimacije kroz epohe.

Slika 14: Usporedba aproksimacije funkcije f(x, y) neuronskom mrežom nakon 200000 epoha i arhitekture (2, 30, 30, 30, 1) sa FEniCS prikazom funkcije f(x, y). Relativna L_{2} pogreška iznosi 0.34\%.

U ovom radu prezentirana je osnovna teorija neuronskih mreža kao aproksimatora te numerički eksperimenti učenja funkcija jedne i dviju varijabli. Proces aproksimacije pomoću neuronske mreže grafički je prikazan tijekom različitih epoha treniranja. Ova vizualna reprezentacija ključna je za demonstriranje postupka učenja neuronske mreže, koja u svojim početnim fazama ne odražava ciljanu funkciju. Numerički eksperimenti za primjer funkcije f(x)= \sin(x) ukazuju da razne arhitekture neuronske mreže vode do pogreške istog reda koristeći MSE funkciju gubitka i relativnu L_{2} pogrešku koristeći Gaussovu integraciju. Demonstriran je problem ekstrapolacije periodičke funkcije, koji je ovdje moguće uspješno riješiti korištenjem periodičnosti funkcije. U dvije dimenzije, na primjeru funkcije f(x, y)=\sin\left(\sqrt{x^{2}+y^{2}}\right), x, y \in [-6, 6], prezentirani su numerički eksperimenti. Problem dvije varijable je kompliciraniji i potrebno je značajno više čvorova, a onda i vremena za treniranje neuronske mreže. Osim standardne funkcije gubitka MSE, kao mjeru točnosti gledamo relativnu pogrešku u L_{2} normi s obzirom na rješenje dobiveno pomoću paketa FEniCS, koji u sebi sadrži funkcije za takve operacije. Nekoliko numeričkih eksperimenta je objavljeno na GitHub platformi i mogu služiti za učenje i rad s Tensorflow 2 paketom, kao i elementima analize točnosti aproksimacije neuronske mreže.{}