Kako zvuče trigonometrijske funkcije?
Magdalena Plemenčić, Ivana Slamić
Sažetak
Prije gotovo dvjesto godina, francuski matematičar i fizičar Joseph Fourier u svom je radu “Theorie analytique de la chaleur” (odnosno u prijevodu “Analitička teorija topline”) predstavio ideju da se bilo koja funkcija definirana na segmentu, čak i ona s prekidima, može prikazati pomoću reda čiji su članovi trigonometrijske funkcije, sinus i kosinus, različitih frekvencija. Iako ta tvrdnja nije bila u potpunosti točna, za određenu (veliku) klasu funkcija ipak vrijedi, a sama ideja prikaza funkcija pomoću takvih redova, odnosno aproksimacija pomoću njegovih parcijalnih suma, potakla je razvoj Fourierove analize, grane matematičke analize koja ima izuzetno važnu ulogu u različitim granama znanosti i tehnike, a posebno u procesiranju signala. U ovom radu opisat ćemo osnovnu ideju primjene Fourierovih redova u analizi i sintezi zvuka.
1Uvod - kako nastaje zvuk?
Velika količina informacija koju primamo svakog dana iz svijeta oko nas dolazi do nas u obliku zvuka - bilo kroz razgovor s drugim ljudima, kroz zvukove s ulice ili prirode, ili slušanjem vijesti na radiju ili televizoru. Neki od tih zvukova su neugodni, neki više ili manje ugodni. Te ugodne nazivamo tonovima, a oni osim glasnoće i visine, posjeduju i boju. Tako ćemo, primjerice, razlikovati je li glazba izvedena na klaviru, violini, gitari ili na nekom drugom instrumentu. No, kako zapravo nastaje zvuk, što on predstavlja i zašto je to uopće važno? U svakodnevnom životu nama, pa ni glazbenicima, razumijevanje kako zvuk nastaje sigurno ne predstavlja veliku važnost, međutim, svakodnevni bi život izgledao mnogo drukčije bez razumijevanja tog procesa. Primjerice, glazbu bismo mogli slušati samo neposredno na koncertu, a vijesti vjerojatno čitali iz novina. Ako se vratimo ponovno na prvu rečenicu, možemo uočiti da su spomenuti zvukovi različitog porijekla. Dok kod prva tri primjera zvuk do nas dolazi direktno iz izvora, u preostalim primjerima je proizveden nekim uređajem na temelju informacije koja je pohranjena u tom uređaju ili elektromagnetskih valova što ih prima antena, te koji su dalje procesirani i pretvoreni u zvuk.
Zvuk grubo možemo opisati kao vibracije koje nastaju zbog promjena u tlaku zraka1 To se događa, primjerice, trzanjem žice gitare, povlačenjem gudala preko žica violine ili pritiskom tipke na klaviru, koje opet uzrokuje udaranje batića po žici. Ako tipku udarimo snažnije, uzrokovat ćemo veće varijacije te će i zvuk kojeg čujemo biti glasniji. Oscilacije u tlaku zraka zvuka kojeg možemo čuti kreću se između 0.00002 Pa i 100 000 Pa. Svakodnevni zvukovi odgovaraju varijacijama u tlaku zraka od 0.00002 Pa do 2 Pa. Kratko izlaganje varijacijama od oko 20 Pa dovodi do oštećenja sluha. S druge strane, bržim varijacijama odgovarat će viši zvuk. Glasnoća zvuka mjerena je u decibelima (dB), gdje je 0 dB prag čujnosti, 80 dB je približna glasnoća usisavača, a 160 dB je glasnoća koja probija bubnjiće. Druga važna karakteristika zvuka je frekvencija, odnosno brzina varijacija. Frekvencija zvučnog vala mjerena je u hercima (Hz) ili brojem ciklusa po sekundi.
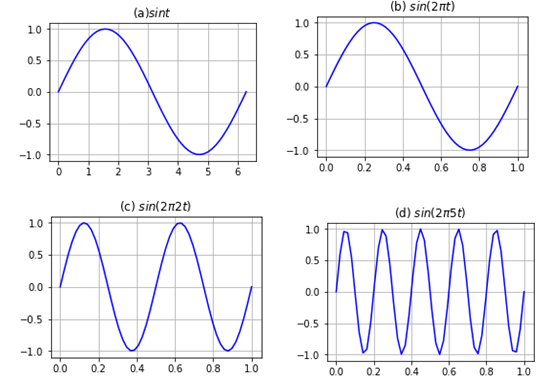
Tlak zraka varira neprekidno kroz vrijeme, stoga se zvuk može matematički predočiti funkcijom. Varijabla te funkcije predstavlja vrijeme, a funkcije u opisanom kontekstu nazivamo signalima. Kako bismo matematički ”opisali varijacije” trebaju nam periodične fukcije. Prvi primjer periodičnih funkcija s kojima se susrećemo u školi su trigonometrijske funkcije - sinus i kosinus. Prisjetimo se, temeljni period funkcije sinus i kosinus jednak je 2 \pi, dok je za \nu \in \mathbb{Z} funkcija f(t)=\sin(2\pi \nu t), t\in \mathbb{R} periodična funkcija s temeljnim periodom \tau=1/\nu. Uočimo da na intervalu [0,1] ova funkcija “oscilira” \nu puta, odnosno taj interval sadrži ukupno \nu intevala duljine temeljnog perioda. To je izraženo činjenicom da f ima frekvenciju \nu. Na slici
Budući da zvuk može biti modeliran funkcijama, zvuk s frekvencijom \nu možemo poistovjetiti s trigonometrijskom funkcijom s frekvencijom \nu. Reći ćemo da je čisti ton s frekvencijom \nu reprezentiran funkcijom t\mapsto \sin(2\pi \nu t), odnosno, čisti ton nastaje ako se frekvencija titranja ne mijenja. U nastavku ćemo vidjeti na koji se način zvuk može prikazati kao “suma čistih tonova”.
2Fourierovi redovi - definicija i osnovna svojstva
U prethodnoj smo cjelini rekli da će u ovom razmatranju važnu ulogu imati periodične funkcije. Prisjetimo se, za funkciju f:\mathbb{R}\to \mathbb{R} kažemo da je periodična ako postoji realan broj \tau\gt 0 takav da je f(t+\tau)=f(t), za svaki t\in \mathbb{R}. Uočimo da je svaku periodičnu funkciju dovoljno zadati na nekom intervalu duljine temeljnog perioda. U nastavku ćemo promatrati periodične funkcije definirane na nekom segmentu te, bez smanjenja općenitosti, možemo pretpostaviti da je taj interval [0,T], gdje je T neki pozitivan realan broj. Sa C[0,T] označavat ćemo skup neprekidnih, realnih funkcija definiranih na tom segmentu. Nije teško pokazati da je skup C[0,T] s operacijama zbrajanja funkcija i množenja funkcija skalarom vektorski prostor. Skalarni produkt na prostoru C[0,T] definiran je sa:
(1)
\langle f,g \rangle = \frac{1}{T} \int_{0}^{T} f(t)g(t)dt,
(2)
\Vert f \Vert _{2} =\sqrt{\frac{1}{T} \int_{0}^{T} f(t)^{2}dt}.
Osnovna ideja Fourierovih2 redova je aproksimirati danu funkciju (konačnim) linearnim kombinacijama funkcija sinus i kosinus, odnosno prikazati funkciju f pomoću reda
(3)
\displaystyle \frac{a_{0}}{2} + \sum_{n=1}^{\infty} (a_{n} \cos{nt}+b_{n} \sin{nt}).
Te linearne kombinacije nazivamo trigonometrijskim polinomima. Neka od najosnovnijih pitanja su sljedeća:
| (1) | {Koliko općenita smije biti funkcija?} |
| (2) | {Kako određujemo koeficijente a_{n}, b_{n}?} |
| (3) | {U kojem smislu red (3) aproksimira polaznu funkciju?} |
Aproksimacija funkcije f pomoću funkcije g u normiranom prostoru s normom (
(4)
T_{N}(t)=a_{0}+ \sum_{n=1}^{N}\Big(a_{n} \cos \frac{2\pi nt}{T}+b_{n} \sin \frac{2\pi nt}{T} \Big),
gdje su brojevi a_{0},...,a_{N} i b_{0},...,b_{N} određeni formulama
(5)
a_{0}=\langle f,1 \rangle =\frac{1}{T} \int_{0}^{T} f(t)dt,
odnosno
(6)
a_{n}=2\Big\langle f, \cos\frac{2\pi n\cdot}{T} \Big\rangle =\frac{2}{T} \int_{0}^{T} f(t)\cos \frac{2\pi nt}{T} dt
i
(7)
b_{n}=2\Big\langle f, \sin \frac{2\pi n\cdot}{T} \Big\rangle =\frac{2}{T} \int_{0}^{T} f(t)\sin \frac{2\pi nt}{T} dt
za n\in\mathbb{N}. Ti brojevi nazivaju se (realni) Fourierovi koeficijenti funkcije f. Dakle, od svih trigonometrijskih polinoma, polinomi s danim koeficijentima najbolje aproksimiraju polaznu funkciju, u smislu najmanjih kvadrata. Može se pokazati da će odstupanje f od tako formiranih trigonometrijskih polinoma, odnosno \Vert f-T_{N}\Vert _{2}, težiti prema 0 kada N teži u beskonačno. To zapravo znači da će parcijalne sume (možemo koristiti oznaku S_{N}f umjesto T_{N}) pripadnog trigonometrijskog reda konvergirati prema 0 u C[0,T] s obzirom na normu (
Fourierove koeficijente možemo definirati i za funkcije koje imaju prekid, ali i za još širu klasu funkcija, ukoliko su gornji integrali konačni (to je ispunjeno, na primjer, ako je |f| integrabilna). Jedna od glavnih zadaća u harmonijskoj analizi je rješavanje pitanja (3), odnosno određivanje uvjeta uz koje Fourierov red konvergira prema polaznoj funkciji. Jedan od teorema tog tipa je Dirichleto3 teorem}.
Teorem 1. (Dirichletov teorem) Neka je f:[0,T] \to \mathbb{R} funkcija tako da vrijedi:
Tada niz parcijalnih suma Fourierovog reda funkcije f konvergira za svaki t \in \mathbb{R} prema nekoj funkciji S:\mathbb{R} \to \mathbb{R}. Ako je funkcija f neprekidna u t \in \langle 0,T \rangle, onda vrijedi S(t)=f(t). Ako funkcija f ima prekid u točki t \in \langle 0,T \rangle, onda je S(t)=\frac{f(t-)+f(t+)}{2}. Nadalje, u krajevima intervala vrijedi S(0)=S(T)=\frac{f(0+)+f(T-)}{2}.
| \bullet | [(i)] f ima najviše konačno mnogo prekida, i to prve vrste (funkcija ima lijevi i desni limes u točki te oni nisu jednaki) na [0,T], |
| \bullet | [(ii)] postoji subdivizija 0=x_{0}\lt x_{1}\lt \ldots\lt x_{n}=T segmenta [0,T] na konačno mnogo dijelova, takva da je funkcija f monotona na svakom segmentu [x_{i},x_{i+1}], i=1,\ldots, n. |
Uvjeti u Teoremu 2.1. nazivaju se Dirichletovi uvjeti za konvergenciju Fourierovih redova.
često se Fourierov red, umjesto u trigonometrijskom, zapisuje u kompleksnom obliku, korištenjem relacija između trigonometrijskih i kompleksne eksponencijalne funkcije:
\cos x=\frac{e^{ix}+e^{-ix}}{2},\quad \sin x=\frac{e^{ix}-e^{-ix}}{2i}.
Fourierove redove moguće je promatrati i za još širu klasu funkcija - Lebesgue integrabilne funkcije. Naime, Fourierove koeficijente moguće je definirati za bilo koju funkciju f\in L^{1}(\mathbb{T}), gdje je \mathbb{T}=\mathbb{R}/ \mathbb{Z}. Skup \mathbb{T} u smislu prostora mjere možemo identificirati sa skupom [0,1\rangle s obzirom na Lebesgueovu mjeru. Za funkcije iz L^{2}(\mathbb{T}) teorija je najpotpunija. Naime, u tom slučaju skup \lbrace e_{k}(\cdot):k\in\mathbb{Z}\rbrace, gdje je e_{k}(x)=e^{2\pi i kx}, čini ortonormiranu bazu za L^{2}(\mathbb{T}), a (kompleksni) Fourierovi koeficijenti \widehat{f}(k)=\langle f,e_{k}\rangle_{L^{2}(\mathbb{T})} predstavljaju koeficijente u rastavu. Postoje različiti teoremi koji razmatraju konvergenciju Fourierovog reda prema polaznoj funkciji. Dok Fourierov red funkcije f\in L^{1}(\mathbb{T}) može divergirati u svakoj točki, ako je funkcija f\in L^{2}(\mathbb{T}), onda njen Fourierov red konvergira prema f gotovo svuda. Rezultat je dokazao Carleson4 1966. godine, a taj se teorem smatra jednim od najdubljih rezultata u harmonijskoj analizi.
Za bilo koju funkciju iz L^{1}(\mathbb{T}), Fourierovi koeficijenti će težiti prema 0 kako n raste. Za primjene će biti važno koliko brzo oni konvergiraju prema 0, jer to može utjecati i na tip konvergencije danog reda. Ako za funkciju dodamo još uvjet diferencijabilnosti klase C^{1}, onda, korištenjem metode parcijalne integracije, možemo pokazati da je \widehat{f '}(n)=\displaystyle\frac{2\pi in}{T} \widehat{f}(n) za svaki n\in\mathbb{N}. Općenitije, što jači uvjet imamo, u smislu diferencijabilnosti (odnosno klase C^{k}), Fourierovi koeficijenti funkcije će brže konvergirati prema nuli.
3Primjeri
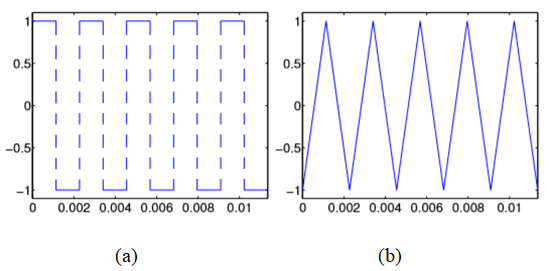
Izračunajmo sada Fourierove koeficijente za dva primjera. Prvi primjer je periodična funkcija, zadana na intervalu duljine temeljnog perioda, [0,T] (gdje je T zadani pozitivan realan broj), na sljedeći način:
(8)
f(t)= \begin{cases} 1, & \quad \text{ako je}\quad 0\leqslant t\lt \frac{T}{2},\\ -1, & \quad \text{ako je}\quad \frac{T}{2}\leqslant t\lt T, \end{cases}
a zatim proširena po periodičnosti na cijeli \mathbb{R}. Ta funkcija u ovom se kontekstu često naziva kvadratni val5}. Za drugi primjer uzmimo periodičnu funkciju, definiranu također na [0,T] na sljedeći način:
(9)
f(t)= \begin{cases} \frac{4t}{T}-1, & \quad \text{ako je}\quad 0\leqslant t\lt \frac{T}{2},\\ 3-\frac{4t}{T}, & \quad \text{ako je} \quad \frac{T}{2}\leqslant t\lt T. \end{cases}
Takva funkcija u ovom se kontekstu često naziva trokutasti val6}. Uočimo jednu bitnu razliku – dok prva funkcija ima prekide u točkama oblika \frac{kT}{2}, k\in\mathbb{Z}, druga funkcija je neprekidna u svakoj točki.
Slika
Primjer 2. Izračunajmo Fourierove koeficijente kvadratnog vala, definiranog sa (4). Dobivamo:
odnosno za n\in\mathbb{N} dobivamo
Prema tome, Fourierov red dan je sa:
Na Slici 3 prikazane su parcijalne sume Fourierovog reda S_{N}f kvadratnog vala kada je T= \frac{1}{440} za N=3, N=5, N=7 i N=9.
(10)
a_{0} =\frac{1}{T} \int_{0}^{T} f(t)dt =\frac{1}{T} \int_{0}^{\frac{T}{2}} dt- \int_{\frac{T}{2}}^{T} dt=0,
\begin{eqnarray*} a_{n} &=&\frac{2}{T} \int_{0}^{T} f(t) \cos \frac{2\pi nt}{T}dt \\ &=& \frac{2}{T}\int_{0}^{\frac{T}{2}} \cos\frac{2\pi nt}{T}dt- \frac{2}{T} \int_{\frac{T}{2}}^{T} \cos \frac{2\pi nt}{T}dt \\ &=&\frac{2}{T} \left[\frac{T}{2\pi n} \sin \frac{2\pi nt}{T}\right]_{0}^{\frac{T}{2}} - \frac{2}{T} \left[\frac{T}{2\pi n} \sin \frac{2\pi nt}{T}\right]_{\frac{T}{2}}^{T} \\ &=&\frac{2}{T}\cdot \frac{T}{2\pi n}((\sin (n\pi)- \sin 0)-(\sin (2\pi n)-\sin (n\pi)))=0\\ \end{eqnarray*}
i
\begin{eqnarray*} b_{n} &=&\frac{2}{T} \int_{0}^{T} f(t) \sin \frac{2\pi nt}{T}dt \\ &=& \frac{2}{T}\int_{0}^{\frac{T}{2}} \sin \frac{2\pi nt}{T}dt- \frac{2}{T} \int_{\frac{T}{2}}^{T} \sin \frac{2\pi nt}{T}dt\\ &=&\frac{2}{T} \left[-\frac{T}{2\pi n} \cos \frac{2\pi nt}{T}\right]_{0}^{\frac{T}{2}} - \frac{2}{T} \left[\frac{T}{2\pi n} \cos \frac{2\pi nt}{T}\right]_{\frac{T}{2}}^{T} \\ &=&\frac{2}{T}\cdot \frac{T}{2\pi n}((-\cos (n\pi)+ \cos 0)+(\cos (2\pi n)-\cos (n\pi))) \\ &=&\frac{2(1- \cos (n\pi))}{n\pi}. \end{eqnarray*}
Dakle, samo su koeficijenti b_{n} s neparnim indeksom n različiti od nula te vrijedi
(11)
b_{n} = \begin{cases} 0, & \quad \text{ako je } n \text{ paran},\\ \nonumber \frac{4}{n\pi}, & \quad \text{ako je } n \text{ neparan}. \nonumber \end{cases}
(12)
\frac{4}{\pi} \sin \frac{2\pi t}{T}+\frac{4}{3\pi}\sin \frac{2\pi 3t}{T}+\frac{4}{5\pi}\sin \frac{2\pi 5t}{T}+\frac{4}{7\pi}\sin \frac{2\pi 7t}{T}+\dots
Slika 3: Grafovi trigonometrijskih polinoma koji predstavljaju parcijalne sume Fourierovog reda kvadratnog vala iz Primjera 3.1.
Primjer 3. Izračunajmo Fourierove koeficijente za trokutasti val, definiran s (5). Vrijedi:
odnosno za n\in\mathbb{N} dobivamo:
i
Stoga Fourierov red za trokutasti val ima sljedeći oblik:
Na Slici 4 prikazani su grafovi parcijalnih suma Fourierovog reda za N=3, N=5, N=7 i N=9.
(13)
a_{0} =\frac{1}{T} \int_{0}^{\frac{T}{2}} \frac{4}{T} \Big(t-\frac{T}{4}\Big)dt +\frac{1}{T}\int_{\frac{T}{2}}^{T} \frac{4}{T}\Big(\frac{3T}{4} -t\Big)dt,
(14)
b_{n} = \frac{2}{T} \int_{0}^{\frac{T}{2}} f(t) \sin \frac{2\pi nt}{T}dt+\frac{2}{T} \int_{\frac{T}{2}}^{T} f(t)\sin \frac{2\pi nt}{T}dt=0
\begin{eqnarray*} a_{n} &=& \frac{2}{T} \int_{0}^{\frac{T}{2}} f(t)\cos \frac{2\pi nt}{T}dt+\frac{2}{T}\int_{\frac{T}{2}}^{T} f(t)\cos \frac{2\pi nt}{T}dt \\ &=&\frac{4}{T}\int_{0}^{\frac{T}{2}} f(t)\cos \frac{2\pi nt}{T}dt =\frac{4}{T}\int_{0}^{\frac{T}{2}}\frac{4}{T} \Big(t-\frac{T}{4}\Big)\cos \frac{2\pi nt}{T}dt\\ &=&\frac{16}{T^{2}}\int_{0}^{\frac{T}{2}} t \cos \frac{2\pi nt}{T}dt - \frac{4}{T} \int_{0}^{\frac{T}{2}}\cos \frac{2\pi nt}{T}dt \\ &=& \frac{4}{n^{2} \pi^{2}} (\cos (n\pi)-1) \\ \end{eqnarray*}
pa je
(15)
a_{n} = \begin{cases} 0, & \quad \text{ako je } n \text{ paran},\\ \frac{-8}{n^{2} \pi^{2}}, & \quad \text{ako je } n \text{ neparan}.\nonumber \end{cases}
(16)
-\frac{8}{\pi^{2}}\cos \frac{2\pi t}{T}-\frac{8}{3^{2} \pi^{2}}\cos \frac{2\pi 3t}{T}-\frac{8}{5^{2} \pi^{2}}\cos \frac{2\pi 5t}{T}-\frac{8}{7^{2} \pi^{2}}\cos \frac{2\pi 7t}{T}+\dots
Slika 4: Grafovi trigonometrijskih polinoma koji predstavljaju parcijalne sume Fourierovog reda trokutastog vala iz Primjera 3.2.
4Funkcija PlaySound u GeoGebri
Zvuk opisan funkcijom lako možemo generirati korištenjem odgovarajućeg softvera, na primjer GeoGebre ili Mathematice. U nastavku dajemo primjere u GeoGebri, koja je prikladna za korištenje i u srednjoj školi prilikom obrađivanja gradiva trigonometrijskih funkcija. Osnovna naredba koju koristimo je:
\texttt{PlaySound(\lt Function\gt ,\lt Min Value\gt ,\lt Max Value\gt ,\lt Sample Rate\gt ,\lt Sample Depth\gt )}.
Prva komponenta sadrži funkciju, druga i treća lijevu i desnu granicu intervala na kojem je funkcija zadana i koja predstavlja trajanje. Tako, primjerice, ako upišemo naredbu PlaySound(sin(2Pi 440 x),0,1), GeoGebra će proizvesti zvuk koji odgovara sinusnom valu, odnosno čistom tonu A_{4} (slika
Uočimo da takvim zbrojem zapravo formiramo trigonometrijske polinome. Mogućnost razvoja u Fourierov red zapravo znači da je određen zvuk moguće prikazati pomoću čistih tonova različitih frekvencija, odnosno, svaki zvuk može biti rekonstruiran ako znamo koje frekvencije sudjeluju u rastavu. To ima veliku ulogu u području koje razmatramo jer sve što moramo pamtiti o zadanom “zvuku”, odnosno funkciji koja ga reprezentira je niz brojeva koji se javljaju u njegovom prikazu. Iz tog niza brojeva, tada znamo i rekonstruirati taj zvuk, ali i jednostavno ga modificirati. Bez obzira je li u program implementiran već “zvuk ostalih funkcija”, npr. ovih iz primjera iz prethodne cjeline, lako ćemo ih moći generirati znamo li Fourierove koeficijente tih funkcija.
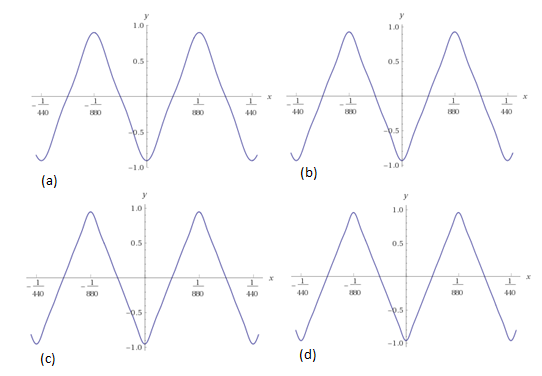
“Odsvirajmo” sada pomoću GeoGebre trigonometrijske polinome koji odgovaraju parcijalnim sumama Fourierovog reda kvadratnog vala iz Primjera 3.1. Ako najprije pogledamo graf, možemo uočiti da je ta funkcija, iako ima isti period T kao i funkcija t\mapsto \sin(2\pi t/T) koja odgovara čistom tonu frekvencije 1/T, u točkama prekida “daleko” od funkcije t\mapsto \sin(2\pi t/T). Kada uključimo sve više tih koeficijenata, trigonometrijski polinom se “približava” sve više polaznoj funkciji, kao što je prikazano na Slici 3. Točnije, “približava” se u smislu da površine što ih zatvaraju grafovi postaju sve manje. S druge strane, prema Dirichletovom teoremu znamo da je to točno i u smislu konvergencije po točkama, u svim točkama osim u točkama gdje funkcija ima prekid, u kojima parcijalne sume konvergiraju prema aritmetičkoj sredini limesa slijeva, odnosno zdesna. što više koeficijenata uključimo, zvuk će biti sličniji zvuku kvadratnog vala, odnosno zvučat će približno ovako:{source=square440.mp3}kvadratni 440 Hz. Uočimo da čisti ton ima samo jedan koeficijent različit od nula, dok kod kvadratnog vala niz Fourierovih koeficijenata konvergira k 0 jednako brzo kao niz 1/n, čineći zvuk manje ugodnim. Kvadratni val “oscilira”, kao i sinusni, T puta svake sekunde, ali dodatni koeficijenti koji nisu nula čine taj zvuk "oštrijim".
Isti postupak možemo primijeniti i za Primjer 3.2, koristeći trigonometrijske polinome prikazane na Slici 4. Za N=1 i T=1/440 taj zvuk je zapravo čisti ton frekvencije 440 Hz. Kako povećavamo N, možemo čuti da uvođenje novih frekvencija čini zvuk manje ugodnim. Kako povećavamo N, trigonometrijski polinom se sve više ”približava” polaznoj funkciji, kao što je prikazano na Slici 4. Primijetimo da je trokutasti val neprekidna funkcija koja zadovoljava uvjete Dirichletovog teorema pa je limes niza parcijalnih suma u svakoj točki jednak vrijednosti te funkcije. Budući da Fourierovi koeficijenti trokutastog vala opadaju kao 1/n^{2} umjesto 1/n kao što je to kod kvadratnog vala, zvuk će, iako i dalje neugodan (zbog različitih frekvencija koje sudjeluju u rastavu), biti manje neugodan nego zvuk kvadratnog vala.
5Zvuk kao “suma čistih tonova”
Vratimo se sada ponovno na rečenicu iz prvog poglavlja gdje je rečeno da će pojedini ton (određen nekom frekvencijom) zvučati različito ovisno o tome na kojem ga instrumentu odsviramo. Primjerice, ton C_{4} odsviran na klaviru zvučat će ovako: {source=c4_new.mp3}klavir c4, a na oboi ovako: {source=oboe.mp3}oboa c4. To je zbog toga što boju tona ne određuje samo fundamentalna frekvencija (odnosno period funkcije koja ga reprezentira), nego niz frekvencija (harmonici ili alikvotni tonovi) koje stvara pojedini instrument, koji ovise o građi instrumenta, ali i o načinu izvođenja pa funkcija koja reprezentira ton iste visine izgleda različito, kao što možemo vidjeti na slici
Slika 6: Različite funkcije pridružene tonu odsviranom na klaviru, oboi te čistom tonu generiranom računalom.
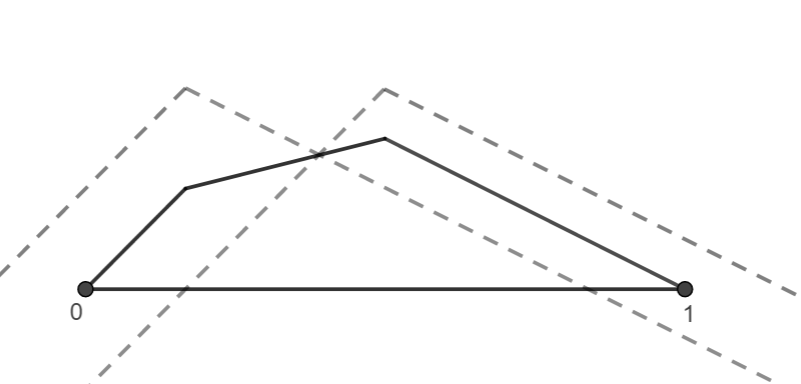
Zvuči neobično, no ne i ako problem razmotrimo s aspekta fizike. Naime, ako napetu žicu učvršćenu na krajevima povučemo (kao, primjerice, kod žičanih instrumenata), to znači da smo je pomaknuli iz početnog položaja. Slika
(17)
\frac{\partial^{2} y}{\partial t^{2}}=c^{2}\frac{\partial ^{2}y}{\partial x^{2}},
pri čemu je c konstanta koja ovisi o duljini, napetosti i masi žice te je pokazao da su rješenja ove jednadžbe oblika
y(x,t)=\Phi(x+ct)+\Psi(x-ct),
gdje su \Phi i \Psi proizvoljne funkcije s neprekidnim derivacijama drugog reda. Ako uključimo pretpostavke da su krajevi žice učvršćeni za x=0 i x=1 te je početni položaj žice opisan funkcijom x\mapsto f(x) na [0,1] u trenutku t=0 te početnom brzinom 0, rješenje je dano s
y(x,t)=\frac{f(x+ct)+f(x-ct)}{2},
pri čemu je f proširena na \mathbb{R} do neparne periodične funkcije s periodom 2. D'Alembert je, promatrajući problem sa strogo matematičkog aspekta, smatrao da je uvjet postojanja derivacija drugog reda nužan u njegovom pristupu. Međutim, Euler nije bio tog mišljenja, odnosno vjerovao je da treba uključiti i funkcije koje nisu nužno diferencijabilne, motiviran vjerojatno činjenicom da postoji početni položaj za koji nije ispunjen prethodni uvjet (slika
Slika 8: činjenicom da je žica učvršćena na krajevima određeno je da se na njenim krajevima stvaraju čvorovi stojnog vala. Prvi red prikazuje najjednostavniji oblik titranja koji se naziva fundamentalni oblik ili prvi harmonik. Dotaknemo li žicu na sredini i stavimo je u titranje, osim dva čvora na krajevima postojat će još jedan čvor na sredini (čvor je mjesto gdje žica miruje). Slika je preuzeta s \url{https://en.wikipedia.org/wiki/Overtone}.
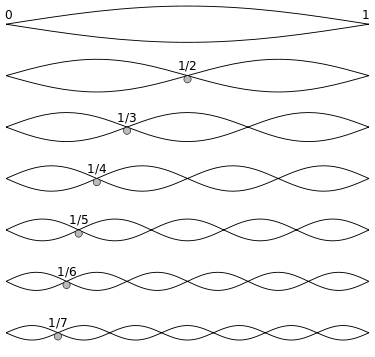
Tada se 1753. godine u raspravu uključio Daniel Bernoulli, koji je dobro poznavao akustiku pa tako i tada već prihvaćenu činjenicu da se ton sastoji od fundamentalne frekvencije i niza alikvotnih tonova. Bernoulli je smatrao da se svako gibanje žice može prikazati u obliku y(x,t)=\sum_{n=1}^{\infty}A_{n}\sin \frac{n\pi x}{\ell}\cos\frac{n\pi ct}{\ell}, uz prikladno odabrane koeficijente A_{n} (uočimo najprije da svaka funkcija u ovom redu zadovoljava jednadžbu (
Pedesetak godina kasnije, Fourier je radio na srodnom problemu širenja topline te je rezultate svojih istraživanja predstavio u radu “Sur la propagation de la chaleur” 1807. godine. Uočio je da se taj problem također može opisati odgovarajućom parcijalnom diferencijalnom jednažbom drugog reda te je tvrdio je da je za rješenje ove jednažbe funkciju koje opisuju početno stanje temperature (definiranu na nekom intervalu) potrebno prikazati pomoću reda koji sadrži funkcije sinus i kosinus (i koji se danas naziva Fourierov red), pri čemu je pokazao kako bi koeficijenti trebali izgledati. Time je pokazao je da je Bernoulli bio u pravu, ali da je i Eulerova primjedba bila točna. Njegova tvrdnja također je uključivala funkcije s prekidima, koje ni D'Alembert ni Euler nisu razmatrali. Međutim, iako su Fourieru i prije ovog rada pristizale potvrde da eksperimenti potvrđuju njegovu teoriju, rad je dočekan sa skepsom, pri čemu je glavna primjedba bila vezana uz nedostatak matematičke strogosti, odnosno uz konvergenciju tog reda. Pokazalo se kasnije da tvrdnja nije bila u potpunosti točna (primjerice, postoji neprekidna funkcija čiji Fourierov red divergira u svim točkama skupa mjere nula), no sam problem zahtijevao je strogi pristup mnogim pojmovima te su rezultati i primjeri iz njegovog rada bili značajni za daljnji razvoj teorije. Rad je objavljen 1822. godine pod nazivom “Théorie analytique de la chaleur”, a rezultat Diricheta iz 1829. godine prvi je rezultat vezan uz konvergenciju Fourierovog reda.
Slika 10: Poznati matematičari koji su radili na problemu vibrirajuće žice: D'Alembert, Euler, D. Bernoulli, Lagrange te Fourier koji je radio na srodnom problemu širenja topline.
6Zaključak
“Profound study of nature is the most fertile source of mathematical discoveries”, rečenica je iz Fourierovog rada, a ideja prikaza funkcije pomoću trigonometrijskih redova pokazala se puno dalekosežnijom od inicijalno promatranih problema vibrirajuće žice ili širenja topline, proširenjem teorije i na klase funkcija koje se u ovim problemima niti ne javljaju u sklopu početnih uvjeta. Pritom su problemi koji su se prirodno javljali (konvergencije, jedinstvenosti itd.), potakli daljnji razvoj matematičke analize, ali i drugih grana teorijske matematike. Također, spektar primjene ove ideje obuhvaća puno više od primjera spomenutih u ovom radu, a posebno je važan u suvremenom svijetu gdje se većina informacija pohranjuje u digitalnom obliku. Samim time primjena ove teorije dosegla je razmjere koje u trenutku njenog stvaranja nisu mogli ni naslutiti.
Bibliografija
Magdalena Plemenčić, studentica Diplomskog sveučilišnog studija Matematika (smjer nastavnički), Sveučilište u Rijeci - Odjel za matematiku, e-mail: magdalenap19@gmail.com
Ivana Slamić, docentica na Odjelu za matematiku Sveučilišta u Rijeci, e-mail: islamic@math.uniri.hr
