|
Dragana Jankov Maširević (1) i Tamara Marković (2) |
|
(1) izv. prof. na Odjelu za matematiku, Sveučilište u Osijeku, Trg Ljudevita Gaja 6, HR-31000 Osijek |
|
(2) Software Engineer u Enea Software d.o.o., Martina Divalta 18, HR-31000 Osijek |
Sažetak U ovom članku upoznat ćemo se s pojmom mjere s predznakom i njezinim rastavom na razliku dviju mjera. Ovakav rastav omogućuju nam dva teorema koja su u literaturi poznata kao Hahnova i Jordanova dekompozicija mjere s predznakom. članak također sadrži nekoliko ilustrativnih primjera koji konkretiziraju navedene pojmove.
1Motivacija
Pojam mjere koristimo svakodnevno: zanima nas dnevna temperatura, duljina puta koji trebamo prijeći do određenog mjesta, površina studentskog stana koji želimo iznajmiti, volumen kutije sladoleda koji namjeravamo kupiti itd. a odgovori na sva prethodna pitanja su nenegativni realni brojevi. Potreba za mjerenjem dovela je i do matematičke discipline Teorije mjere} koja izučava pojmove poput duljine, površine i volumena, pod zajedničkim nazivom mjera} [14]. Općenito, objekti mjerenja (preciznije, izmjerivi skupovi) su elementi neke unaprijed zadane familije \mathcal{A} podskupova nepraznog skupa X koju nazivamo {\sigma–algebra}}, a ona sadrži cijeli X te je zatvorena na komplementiranje i formiranje prebrojivih unija. Mjera} je, zatim, svaka funkcija \mu\colon\mathcal{A}\to\mathbb{\overline{R}} koja zadovoljava sljedeća, jednostavna svojstva:
-
-
[(\mu1)] \mu(\emptyset)=0,
-
-
[(\mu2)](nenegativnost) \mu(A)\geq0 za svaki A\in\mathcal{A},
-
-
[(\mu3)](\sigma-aditivnost) za niz disjunktnih skupova (A_{n})_{n\in\mathbb{N}} iz \mathcal{A} vrijedi
\begin{align*} \mu\Big(\bigcup_{n\in\mathbb{N}}A_{n}\Big)=\sum_{n\in\mathbb{N}}\mu(A_{n}). \end{align*}
Svojstvo analogno svojstvu \sigma-aditivnosti, ali s konačno mnogo disjunktnih skupova, nazivamo konačna aditivnost} te je jasno da \sigma–aditivnost povlači konačnu aditivnost dok obrat ne vrijedi.
Bitno je još naglasiti da je uređeni par (X,\mathcal{A}) uobičajeno zvati izmjeriv prostor}, dok uređenu trojku (X,\mathcal{A},\mu) nazivamo prostor mjere}. Kako bi bolje razumjeli ono što slijedi, spomenimo da za skup A\in\mathcal{A} kažemo da je skup konačne mjere ako je \mu(A)\lt \infty, dok za mjeru \mu kažemo da je konačna ako je \mu(X)\lt \infty; nadalje, bitno je istaknuti da je mjera \mu vjerojatnost} ili vjerojatnosna mjera} ako je \mu(X)=1.
Također, na prostoru mjere (X,\mathcal{A},\mu) vrijede sljedeća svojstva:
|
\bullet |
(monotonost) Za svaka dva skupa A,B\in \mathcal{A} takva da je A\subseteq B vrijedi \mu(A)\leq\mu(B). Dodatno, ako je skup A konačne mjere, tada je \mu(B\setminus A)=\mu(B)-\mu(A). |
|
\bullet |
(\sigma-subaditivnost) Za svaki niz (A_{n})_{n\in\mathbb{N}} skupova iz \mathcal{A} vrijedi
\begin{align*} \mu\Big(\bigcup_{n\in\mathbb{N}}A_{n}\Big)\leq\sum_{n\in\mathbb{N}}\mu(A_{n}). \end{align*}
|
|
\bullet |
(neprekidnost na rastuće nizove) Za svaki rastući niz (A_{n})_{n\in\mathbb{N}} skupova iz \mathcal{A} vrijedi
\begin{align*} \mu\Big(\bigcup_{n\in\mathbb{N}}A_{n}\Big)=\lim_{k\to\infty}\mu(A_{k}). \end{align*}
|
|
\bullet |
(neprekidnost na padajuće nizove) Za svaki padajući niz (A_{n})_{n\in\mathbb{N}} skupova iz \mathcal{A}, takav da je \mu(A_{1})\lt \infty, vrijedi
\begin{align*} \mu\Big(\bigcap_{n\in\mathbb{N}}A_{n}\Big)=\lim_{k\to\infty}\mu(A_{k}). \end{align*}
|
Prirodno je pitati se možemo li iskoristiti već poznate mjere za generiranje novih mjera. Lako se pokaže da je zbroj dviju ili više mjera opet mjera \cite[str. 36]{DJM}. Na žalost, množenje mjere skalarom ne rezultira uvijek mjerom, jer ako je dani skalar negativan realan broj, tada uvjet nenegativnosti nije ispunjen. Ipak, negativnost našeg skalara ne utječe na preostala dva svojstva mjere što otvara mogućnost za generalizaciju ovog pojma. Također, razlika mjera ne mora ponovno biti mjera –štoviše, može se dogoditi da ta razlika uopće nije definirana \cite[str. 8]{TM}. Dakle, možemo li kao rezultat mjerenja dobiti negativan broj?
Kako bi razriješili prethodno pitanje, u nastavku ćemo se baviti mjerama s predznakom}, što je poopćenje pojma mjere na način da se izostavi svojstvo nenegativnosti. Također, saznat ćemo i što je to realna mjera te ćemo pokazati da je integral integrabilne funkcije (funkcije čiji je integral konačan s obzirom na danu mjeru) na izmjerivom skupu realna mjera. Sve to, nadopunit ćemo bitnim svojstvima. Na posljetku ćemo, kada se dobro upoznamo s pojmovima vezanim uz mjere s predznakom, definirati Hahnovu i Jordanovu dekompoziciju. Naime, austrijski matematičar H. Hahn je 1921. [11] objavio svoj čuveni teorem, koji po njemu nosi i ime (vidi Teorem 18) i daje dekompoziciju skupa X na dva njegova disjunktna podskupa od kojih je jedan pozitivne, a drugi negativne mjere s predznakom. Nadalje, francuski matematičar C. Jordan dao je dokaz rastava realne funkcije omeđene varijacije na razliku dvije nenegativne monotone funkcije. Prirodna posljedica ove tvrdnje je dekompozicija mjere s predznakom, za koju se glavna ideja pripisuje francuskom matematičaru H. L. Lebesgueu, vidi str. 353 iz [21]. Bitno je naglasiti i da je Jordanova dekompozicija jedinstvena i ona nam znatno olakšava rad s mjerama s predznakom.
Primjene mjere s predznakom su mnogobrojne, pogotovo u fizici. Naime, mjeru s predznakom možemo poistovjetiti s raspodjelom električnog naboja; preciznije, mjera s predznakom nekog skupa A predstavlja ukupni naboj sadržan u A. Zbog toga se mjere s predznakom ponekad nazivaju naboji (engl. charges) vidi str. 58, Remark [19]. Također, mjeru često poistovjećujemo s raspodjelom mase na glavnom skupu X, dok konačnu mjeru s predznakom (koju ćemo zvati i realna mjera) možemo interpretirati kao (električnu) raspodjelu naboja na X. Posljedica Jordanove dekompozicije, za konačne mjere s predznakom (iskazana u Korolaru 21) opravdava ovu metaforu pokazujući da kao kod naboja u elektrostatikama, postoje dva disjunktna skupa od koji je jedan pozitivnog, a drugi negativnog naboja, vidi str. 108 iz [3]. Nadalje, kako je vjerojatnost zapravo specijalna mjera, u literaturi također možemo pronaći pojam negativne vjerojatnosti odnosno vjerojatnosti s predznakom (čitatelj može pročitati više u [1, 4]) koja ima primjenu u fizici i financijama [4, 5, 7, 10, 13, 23].
Zainteresirani čitatelj u literaturi može pronaći i Lebesgueovu dekompoziciju [14, 18] koja daje (jedinstven) rastav \sigma-konačne mjere (mjere koja omogućava rastav skupa X na prebrojivu uniju skupova konačne mjere) na zbroj dviju mjera te ima važnu primjenu u teoriji vjerojatnosti pri računanju vjerojatnosti i matematičkog očekivanja miješanih slučajnih varijabli (eng. mixed random variables) o čemu čitatelj može pročitati npr. u [8, 16, 17, 20].
2Mjera s predznakom
U nastavku najprije navodimo preciznu definiciju mjere s predznakom, najavljenu u uvodnom dijelu.
Definicija 1. Neka je
(X, \mathcal{A}) izmjeriv prostor. Mjera s predznakom je svako preslikavanje
\mu \colon \mathcal{A} \to \mathbb{\overline{R}} sa svojstvima
|
1) |
\mu(\emptyset)=0, |
|
2) |
(\sigma-aditivnost) za svaki niz (A_{n})_{n \in \mathbb{N}} disjunktnih skupova iz \mathcal{A} vrijedi
\begin{align*} \mu\Big( \bigcup\limits_{n \in \mathbb{N}} A_{n} \Big)=\sum\limits_{n \in \mathbb{N}} \mu( A_{n} ). \end{align*}
|
Iz prethodne definicije je očito da je svaka mjera ujedno i mjera s predznakom te da obrat ne vrijedi. Također, lako je uočiti ako je \mu mjera, tada je \alpha \mu mjera s predznakom za svaki \alpha\in\mathbb{R}.
U literaturi se pri definiranju mjere s predznakom često navodi uvjet da funkcija \mu ne smije istovremeno poprimati vrijednost -\infty i +\infty (vidi npr. [2, 19, 22]). U nastavku ćemo pokazati da se ovaj uvjet ne treba posebno isticati, vidi str. 114 iz [6].
Napomena
Neka je \mu mjera s predznakom na izmjerivom prostoru (X,\mathcal{A}) i A \in \mathcal{A} proizvoljan skup. Skup X možemo prikazati kao uniju skupova A i A^{c}, koji su disjunktni, te prema \sigma-aditivnosti mjere s predznakom slijedi
\mu(X)=\mu(A)+\mu(A^{c}).
Iz prethodne jednakosti vidimo da ako je \mu(A)=\infty tada je nužno \mu(X)=\infty, a u tom slučaju \mu(A^{c}) poprima konačnu vrijednost ili je također jednako +\infty, jer u suprotnom desna strana ne bi bila dobro definirana. Analogno zaključujemo u slučaju kada je \mu(A)=-\infty.
U sljedećoj propoziciji dokazat ćemo da je razlika svake dvije mjere, od kojih je jedna konačna, mjera s predznakom (vidi str. 190 iz [14]).
Propozicija 2. Neka su
\mu_{1} i
\mu_{2} dvije mjere na izmjerivom prostoru
(X,\mathcal{A}). Ukoliko je barem jedna od danih mjera konačna, tada je s
\mu_{2}-\mu_{1} definirana mjera s predznakom na
(X,\mathcal{A}).
Dokaz. Bez smanjenja općenitosti, neka je \mu_{1} konačna mjera. Funkcije \mu_{1} i \mu_{2} su mjere, stoga je \mu_{1}(\emptyset)=\mu_{2}(\emptyset)=0 što povlači (\mu_{2}-\mu_{1})(\emptyset)=0. Nadalje, neka je (A_{n})_{n \in \mathbb{N}} niz disjunktnih skupova iz \mathcal{A}. Primjenom \sigma-aditivnosti za mjere dobivamo
\begin{align*} (\mu_{2}-\mu_{1})\Big(\bigcup_{n \in \mathbb{N}}A_{n}\Big)=\sum_{n \in \mathbb{N}}(\mu_{2}-\mu_{1})(A_{n}). \end{align*}
Kako razlika dvije mjere općenito nije nenegativan broj, slijedi da je \mu_{2}-\mu_{1} mjera s predznakom. \Box
Primijetimo da se uvjet konačnosti jedne od mjera iz Propozicije 2 ne smije izostaviti, jer se u suprotnom može dogoditi da izraz \mu_{2}-\mu_{1} nije definiran. Potaknuti tim razmišljanjem, u nastavku ćemo definirati realnu mjeru.
Definicija 3. Mjera s predznakom je konačna, ako je
|\mu(A)| \lt \infty za svaki izmjeriv skup
A. Konačnu mjeru s predznakom zovemo realna mjera.
Uočimo da je oznaka |\mu(A)|\lt \infty zapravo kraći oblik zapisa: -\infty\lt \mu(A)\lt \infty
(ili \mu(A) \in \mathbb{R}). Dakle, mjera s predznakom je konačna ako ne poprima vrijednosti \pm\infty. U Propoziciji 7, u nastavku, navest ćemo jedan bitan primjer realne mjere, odnosno dokazat ćemo da je integral integrabilne funkcije na izmjerivom skupu realna mjera.
Kako bi se uvjerili u istinitost dane tvrdnje, u dokazu će nam biti korisno poznavati definiciju karakteristične funkcije \chi_{A}\colon X\to\mathbb{R}, nekog skupa A\subseteq X, danu s
\begin{align*} \chi_{A}(x)= \begin{cases} 1,&\text{ ako je }x\in A\text{}\\ 0,&\text{ ako }x\notin A\text{}. \end{cases} \end{align*}
Bitno je istaknuti da je \chi^{}_{A} izmjeriva funkcija ako i samo ako je A izmjeriv skup, vidi str. 97 [14]. Općenito, ako imamo izmjerive prostore (X,\mathcal{A}) i (Y,\mathcal{B}) te skup A\subseteq X, za funkciju f:A\to Y kažemo da je izmjeriva u paru \sigma–algebri \mathcal{A} i \mathcal{B} ili kraće \mathcal{A}-\mathcal{B} izmjeriva ako je f^{-1}(B)\in\mathcal{A}, za svaki B\in\mathcal{B}. Ukoliko je (Y,\mathcal{B})\equiv(\mathbb{R},\mathcal{B}(\mathbb{R})) ili (Y,\mathcal{B})\equiv(\mathbb{\overline{R}},\mathcal{B}(\mathbb{\overline{R}})), gdje je \mathcal{B}(\mathbb{R}) tzv. Borelova \sigma–algebra na \mathbb{R}, odnosno \mathcal{B}(\mathbb{\overline{R}}) Borelova \sigma–algebra na \mathbb{\overline{R}}, za funkciju f kažemo da je \mathcal{A}–izmjeriva, ili kraće izmjeriva.
Također, u nastavku će nam biti potreban i pojam integrala ( po mjeri) izmjerive funkcije, koji, u skladu s literaturom (vidi npr. [6, 14]) uvodimo u tri koraka: naprije se definira integral nenegativne jednostavne funkcije, što je izmjeriva i stepenasta (poprima samo konačno mnogo vrijednosti) funkcija, koji se zatim može proširiti do integrala nenegative izmjerive funkcije te se u trećem koraku pravi proširenje do integrala proizvoljne izmjerive funkcije.
Naime, koristeći činjenicu da se svaka jednostavna funkcija f\colon A\to\mathbb{R}, na izmjerivom prostoru (X,\mathcal{A}), gdje je A\subseteq X, može prikazati u obliku
(1)
f=\sum\limits_{i=1}^{n}\alpha_{i}\chi_{A_{i}},
gdje su \alpha_{1},\dots,\alpha_{n} različiti realni brojevi te A_{1},\dots,A_{n} disjunktni izmjerivi skupovi takvi da je A=\bigcup\limits_{i=1}^{n} A_{i}, vrijedi sljedeće:
Definicija 4. Neka je
(X,\mathcal{A},\mu) prostor mjere i
f\colon X\to[0,\infty\rangle nenegativna jednostavna funkcija s prikazom
(1), gdje su
\alpha_{1},\dots,\alpha_{n} nenegativni realni brojevi te
A_{1},\dots,A_{n} disjunktni izmjerivi skupovi.
|
\bullet |
Broj
\displaystyle \int fd\mu:=\sum_{i=1}^{n}\alpha_{i}\mu(A_{i})
se zove integral funkcije f s obzirom na mjeru \mu ili, kraće, integral funkcije f. Za funkciju f kažemo da je integrabilna ako je \int fd\mu\lt \infty. |
|
\bullet |
Neka je E\in\mathcal{A} izmjeriv skup. Broj \displaystyle \int\limits_{E} fd\mu:=\int\chi_{E} fd\mu=\sum_{i=1}^{n}\alpha_{i}\mu(E\cap A_{i}) se zove integral funkcije f na skupu E s obzirom na mjeru \mu ili, kraće, integral funkcije f na skupu E. Za funkciju f kažemo da je integrabilna na skupu E ako je \int\limits_{E} fd\mu\lt \infty. |
Skup svih nenegativnih jednostavnih funkcija uobičajeno je označavati s \mathcal{F}_{+}.
Nadalje, kako se svaka nenegativna izmjeriva funkcija f:X\to[0,\infty], na prostoru mjere (X,\mathcal{A},\mu), može aproksimirati s nenegativnom jednostavnom funkcijom g\in\mathcal{F}_{+}, g\le f (za više detalja vidi npr. str. 104, Teorem 3.23 iz [14]), dolazimo do sljedećeg proširenja integrala na skup svih nenegativnih izmjerivih funkcija:
Definicija 5. Neka je
(X,\mathcal{A},\mu) prostor mjere i
f\colon X\to[0,\infty] nenegativna izmjeriva funkcija.
|
\bullet |
Broj
\int fd\mu:=\sup\left\lbrace \,\int gd\mu:\,g\in\mathcal{F}_{+},\, g\leq f\,\right\rbrace
se zove integral funkcije f s obzirom na mjeru \mu ili, kraće, integral funkcije f. Za funkciju f kažemo da je integrabilna ako je \int fd\mu\lt \infty. |
|
\bullet |
Neka je E\in\mathcal{A} izmjeriv skup. Broj \displaystyle \int\limits_{E} fd\mu:=\int\chi_{E} fd\mu se zove integral funkcije f na skupu E s obzirom na mjeru \mu ili, kraće, integral funkcije f na skupu E. Za funkciju f kažemo da je integrabilna na skupu E ako je \int\limits_{E} fd\mu\lt \infty. |
Na posljetku, koristeći tvrdnju da za svaku izmjerivu funkciju f:A\to\mathbb{\overline{R}} postoje nenegativne izmjerive funkcije f^{+},f^{-}:A\to [0,\infty], definirane formulama, vidi str. 102 iz [14]
f^{+}(x)=\max\lbrace f(x),0\rbrace ,\qquad f^{-}(x)=-\min\lbrace f(x),0\rbrace ,\qquad x\in A,
koje zovemo pozitivni i negativni dio funkcije f, redom, te vrijedi
dolazimo do fundamentalne definicije integrala:
Definicija 6. Neka je
(X,\mathcal{A},\mu) prostor mjere i
f\colon X\to\overline{\mathbb{R}} izmjeriva funkcija.
|
\bullet |
Ako je barem jedan od brojeva \int f^{+} d\mu i \int f^{-} d\mu konačan, onda se definira broj
\int fd\mu:=\int f^{+} d\mu-\int f^{-} d\mu
i zovemo ga integral funkcije f s obzirom na mjeru \mu ili, kraće, integral funkcije f. Za funkciju f kažemo da je integrabilna ako je \int fd\mu\lt \infty. |
|
\bullet |
Neka je E\in\mathcal{A} izmjeriv skup. Ako je definiran integral \int\limits_{E} fd\mu, onda broj \displaystyle \int\limits_{E} fd\mu:=\int\chi_{E} fd\mu zovemo integral funkcije f na skupu E s obzirom na mjeru \mu ili, kraće, integral funkcije f na skupu E. Za funkciju f kažemo da je integrabilna na skupu E ako je \int\limits_{E} fd\mu\lt \infty. |
Sada smo spremni iskazati sljedeću propoziciju.
Propozicija 7. Neka je
(X,\mathcal{A},\mu) prostor mjere i
f\colon X\to \mathbb{\overline{R}} integrabilna funkcija. Funkcija
\nu\colon\mathcal{A}\to \mathbb{\overline{R}} definirana s
\begin{align*} \nu(E):=\int\limits_{E} fd\mu\equiv\int\limits f\chi_{E}d\mu,\hspace{5ex}\;za\;svaki\; E \in \mathcal{A}, \end{align*}
je realna mjera.
Dokaz. Očito je \nu(\emptyset)=0. Nadalje, neka je (A_{n})_{n\in\mathbb{N}} niz disjunktnih i izmjerivih skupova. Uz pomoć prethodno opisanog rastava (??), dobivamo
\begin{align*} \nu\Big(\bigcup_{n\in\mathbb{N}}A_{n}\Big)&=\int f\chi^{}_{\cup^{}_{n\in\mathbb{N}}A_{n}}d\mu=\int f^{+}\chi^{}_{\cup^{}_{n\in\mathbb{N}}A_{n}}d\mu-\int f^{-}\chi^{}_{\cup^{}_{n\in\mathbb{N}}A_{n}}d\mu\\ &=\int f^{+}\sum_{n\in\mathbb{N}}\chi_{A_{n}}d\mu-\int f^{-}\sum_{n\in\mathbb{N}}\chi_{A_{n}}d\mu=\sum_{n\in\mathbb{N}}\int f^{+}\chi_{A_{n}}d\mu-\sum_{n\in\mathbb{N}}\int f^{-}\chi_{A_{n}}d\mu\\ &=\sum_{n\in\mathbb{N}}\int f\chi_{A_{n}}d\mu=\sum_{n\in\mathbb{N}}\nu(A_{n}), \end{align*}
pri čemu smo u trećoj jednakosti koristili da je \displaystyle \chi^{}_{\cup^{}_{n\in\mathbb{N}}A_{n}}=\sum_{n\in\mathbb{N}}\chi_{A_{n}}, za niz (A_{n})_{n\in\mathbb{N}} međusobno disjunktnih skupova, vidi str. 12, Zadatak 1.16. [15], a u četvrtoj jednakosti Levijev teorem za redove (vidi str. 129, Teorem 4.22. [14]), koji vrijedi za nenegativne izmjerive funkcije, što je razlog korištenja rastava dane funkcije f na f^{+} i f^{-}. \Box
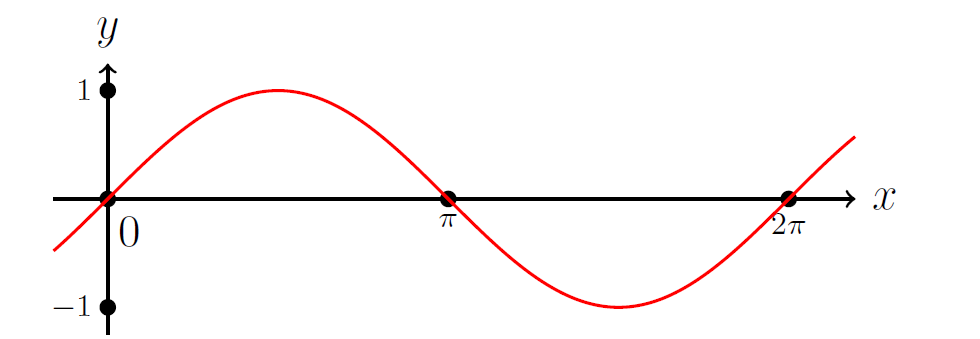
Primjer 8. Na danom prostoru mjere
([\pi,2 \pi],\mathcal{B}(\mathbb{R}),\lambda), gdje je
\mathcal{B}(\mathbb{R}) Borelova
\sigma–algebra, a
\lambda Lebesgueova mjera na
[\pi, 2 \pi] izračunajmo integral funkcije
f(x)=\sin{x} koja je negativna na
[\pi,2 \pi] (vidi
Sliku 1).
Graf funkcije \[y=\sin(x)\]
Koristeći Lebesgueov kriterij za R–integrabilnost (koji omogućava izjednačavanje Riemannovog i Lebesgueovog integrala, u slučaju kada je podintegralna funkcija omeđena i neprekidna skoro svuda, odnosno
R–integrabilna na svojoj domeni koja je neki konačan skup, vidi str. 150, Teorem 4.53
[14]) slijedi da je
\int_{[\pi,2 \pi]}\sin{x}\,d\lambda=\int\limits_{\pi}^{2 \pi}\sin{x}\,dx=-2 \lt 0.
Dakle, kao rezultat mjerenja dobili smo negativan broj, a naš rezultat opravdava prethodna propozicija.
\blacksquare
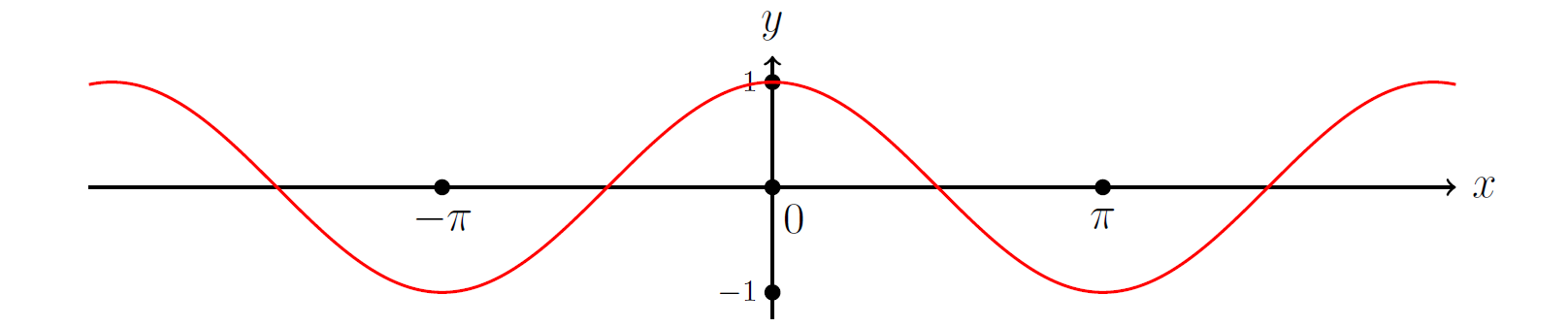
U idućem primjeru vidjet ćemo da mjera s predznakom općenito ne zadovoljava svojstvo monotonosti, pri čemu će nam ponovno poslužiti Propozicija 7, s obzirom da podintegralna funkcija f(x)=\cos{x} nije nenegativna na cijeloj svojoj domeni (vidi Sliku 2).
Primjer 9. Neka je dan prostor mjere
([-\pi,\pi],\mathcal{B}(\mathbb{R}),\lambda). Ako je mjera s predznakom
\mu (vidi
Propoziciju 7) definirana s
\mu(E)=\int\limits_{E} \cos{x}\,d\lambda,\,\,{\text{za svaki }}E\in\mathcal{B}(\mathbb{R}),
lako je, uz pomoć Lebesgueovog kriterija za R–integrabilnost odrediti vrijednosti
\begin{align*} \mu\left(\left[-\pi,\textstyle\frac{\pi}{2}\right]\right)&=\int_{\left[-\pi,\frac{\pi}{2}\right]} \cos{x}\,d\lambda=\int\limits_{-\pi}^{\textstyle\frac{\pi}{2}} \cos{x}\,dx=1,\\ \mu([-\pi,\pi])&=\int\limits_{[-\pi,\pi]} \cos{x}\,d\lambda=\int_{-\pi}^{\pi} \cos{x}\,dx=0. \end{align*}
Očito je
\left[-\pi,\frac{\pi}{2}\right]\subset[-\pi,\pi] te
\mu\left(\left[-\pi,\frac{\pi}{2}\right]\right)\gt \mu([-\pi,\pi]) iz čega zaključujemo da mjera s predznakom ne zadovoljava svojstvo monotonosti.
Graf funkcije \[y=\cos(x)\].
\blacksquare
Iako mjera s predznakom nema svojstvo monotonosti, ona djelomično zadovoljava to svojstvo:
Propozicija 10. Neka je
\mu mjera s predznakom na izmjerivom prostoru
(X,\mathcal{A}) i neka su
A, B \in \mathcal{A} takvi da je
A \subseteq B. Tada vrijedi
|
i) |
Ako je \mu(B) \in \mathbb{R}, onda je \mu(A) \in \mathbb{R}. |
|
ii) |
Ako je \mu(A)=\infty, onda je \mu(B)=\infty. |
|
iii) |
Ako je \mu(A)=-\infty, onda je \mu(B)=-\infty. |
|
iv) |
Ako je \mu(A) \in \mathbb{R}, onda je \mu(B \setminus A)=\mu(B)-\mu(A). |
Dokaz. Za skupove A i B dane u iskazu propozicije vrijedi jednakost B=A \cup( B \setminus A), pri čemu su A i B \setminus A međusobno disjunktni pa primjenom konačne \sigma-aditivnosti mjere s predznakom dobivamo
(\textasteriskcentered)
\begin{align} \mu(B)=\mu(A)+\mu(B \setminus A). \end{align}
|
i) |
Neka je \mu(B) \in \mathbb{R}. Kada bi bilo \mu(A)=\pm\infty, zbog \infty \pm a=\infty te zbog -\infty \pm a=-\infty, za svaki a \in \mathbb{R}, tada bi dobili \mu(B)=\pm\infty. Slijedi da je \mu(A)\in\mathbb{R}. |
|
ii) |
Ako je \mu(A)=\infty, tada je nužno \mu(B\setminus A)\neq-\infty, jer mjera s predznakom ne može istovremeno poprimiti vrijednost -\infty i +\infty. Iz prethodnog slijedi da je \mu(B)=\infty. Analogno dokazujemo i tvrdnju iii). |
|
iv) |
Neka je \mu(A) \in \mathbb{R}. Tada je dobro definiran izraz \mu(B)-\mu(A) te prema (??) vrijedi da je \mu(B \setminus A)=\mu(B)-\mu(A). |
\Box
Teorem 11. Neka je
\mu mjera s predznakom na izmjerivom prostoru
(X,\mathcal{A}). Tada ona zadovoljava svojstva {
neprekidnosti na rastuće i {
neprekidnosti na padajuće nizove.
Dokaz, koji je tehnički i oponaša dokaz tvrdnje o neprekidnosti mjere na padajuće i rastuće nizove, može se pronaći u npr. str. 207, Theorem 10.8 [22]. \Box
3Hahnova i Jordanova dekompozicija
U Propoziciji 2 pokazali smo da je razlika dviju mjera, od kojih je jedna konačna, mjera s predznakom. U nastavku ćemo pokazati da vrijedi i obrat, to jest da se mjera s predznakom može na jedinstven način prikazati kao razlika dviju mjera. Glavna ideja dokaza je ta da krenemo od pretpostavke da je mjera s predznakom \mu poopćenje neke mjere. Ako je to tako, onda sigurno mora postojati izmjeriv skup A za koji će vrijediti \mu(A)\geq 0 te izmjeriv skup B za koji je \mu(B)\leq 0. Teorem 18 će nam omogućiti maksimalnost i disjunktnost tih skupova. Bez smanjenja općenitosti, pretpostavimo da su A i B već takvi skupovi. Tada je restrikcija mjere s predznakom \mu na skup A mjera. Vrijedi i da je \mu(B)\leq 0 odnosno -\mu(B)\geq 0. Tada će funkcija -\mu_{|_{B}} također biti mjera. Pritom, moramo paziti da nemamo degeneriranih slučajeva (npr. za C\subseteq A vrijedi da je \mu(C)\lt 0). Idućom definicijom eliminirat ćemo tu mogućnost.
Definicija 12. Neka je
\mu mjera s predznakom na izmjerivom prostoru
(X, \mathcal{A}). Za skup
A \in \mathcal{A} kažemo da je
|
i) |
pozitivan skup s obzirom na \mu ako je \mu(E)\geq 0, za svaki E\in \mathcal{A}, E \subseteq A; |
|
ii) |
negativan skup s obzirom na \mu ako je \mu(E)\leq 0, za svaki E\in \mathcal{A}, E \subseteq A; |
|
iii) |
nul–skup s obzirom na \mu ako je \mu(E)=0, za svaki E\in \mathcal{A}, E \subseteq A. |
Napomena.
Trivijalne posljedice Definicije 12 su:
|
i) |
ako je skup A pozitivan {\,negativan, nul–\,]}} s obzirom na \mu, tada je \mu(A)\geq 0 {\,\mu(A)\leq 0, \mu(A)=0\,]}}, ali obrat općenito ne vrijedi (vidi Primjer 13). |
|
ii) |
Skup A je nul–skup s obzirom na \mu ako i samo ako je A istovremeno pozitivan i negativan skup s obzirom na \mu. |
U nastavku navodimo primjere koji ilustriraju prethodne tvrdnje.
Primjer 13. Neka je
\mu\colon\mathcal{P}(\mathbb{N}) \to \mathbb{R} realna mjera na izmjerivom prostoru
(\mathbb{N},\mathcal{P}(\mathbb{N})) definirana s
\begin{align*} \mu(E):= \begin{cases} \hphantom{-}1,& \lbrace 1\rbrace \subseteq E\; i\; \lbrace 3\rbrace \nsubseteq E\\ -1,& \lbrace 1\rbrace \nsubseteq E\; i\; \lbrace 3\rbrace \subseteq E\\ \hphantom{-}0,& \text{inače}, \end{cases} \hspace{5ex}{\text{za svaki }}E \in \mathcal{A}. \end{align*}
Lako je uočiti da je
\mu(\mathbb{N})=0, odnosno skup
\mathbb{N} je mjere nula, no kako je, na primjer,
\lbrace 1\rbrace \subseteq\mathbb{N} i
\mu(\lbrace 1\rbrace )=1\neq 0, prema
Definiciji 12 slijedi da
\mathbb{N} nije nul–skup.
\blacksquare
Primjer 14. S obzirom na mjeru s predznakom
\nu iz
Propozicije 7 skup
P=\lbrace x \in X:f(x) \geq 0\rbrace je pozitivan. Naime, kako za proizvoljan skup
A\subseteq P vrijedi
f(x) \geq 0 za sve
x \in A, to je
\nu(A)=\int_{A} fd\mu=\int f \chi_{A} d\mu\geq 0.
Na isti način možemo zaključiti da je skup
N=\lbrace x \in X:f(x) \leq 0\rbrace negativan, a skup
Z=\lbrace x \in X:f(x)=0\rbrace nul–skup s obzirom na
\nu.
\blacksquare
Uz pomoć sljedećih propozicija, koje tvrde da je svaki podskup pozitivnog [\,negativnog, nul–\,] skupa, opet pozitivan [\,negativan, nul–\,] skup (Propozicija 15) te da je familija svih pozitivnih [\,negativnih, nul–\,] skupova zatvorena s obzirom na prebrojivu uniju njezinih članova (Propoziciji 17) dobit ćemo koristan alat za stvaranje novih pozitivnih [\,negativnih, nul–\,] skupova.
Propozicija 15. Neka je
\mu mjera s predznakom na izmjerivom prostoru
(X,\mathcal{A}). Svaki izmjeriv podskup negativnog skupa je negativan skup. Tvrdnja vrijedi i za pozitivne i za nul–skupove.
Dokaz. Neka je A \in \mathcal{A} negativan skup s obzirom na \mu i neka je B \in \mathcal{A},\; B \subseteq A. Tada, po Definiciji 12 i tranzitivnosti relacije \subseteq, za svaki C \in \mathcal{A},\; C \subseteq B vrijedi \mu(C) \leq 0. \Box
Napomena
Iz Napomene i) te Propozicije 15 možemo zaključiti da ako je A \in \mathcal{A} pozitivan skup s obzirom na \mu i B \in \mathcal{A} negativan skup s obzirom na \mu, tada je A \cap B nul–skup s obzirom na \mu.
Sljedeći teorem daje karakterizaciju pozitivnih, negativnih i nul–skupova s obzirom na \mu i može se pronaći u literaturi (vidi npr. [12, 14]) kao definicija pozitivnog [\,negativnog, nul-\,] skupa.
Teorem 16. Neka je
\mu mjera s predznakom na izmjerivom prostoru
(X, \mathcal{A}). Skup
A \in \mathcal{A} je
|
i) |
pozitivan skup s obzirom na \mu ako i samo ako je \mu(A \cap F) \geq 0, za svaki F \in \mathcal{A}, |
|
ii) |
negativan skup s obzirom na \mu ako i samo ako je \mu(A \cap F) \leq 0, za svaki F \in \mathcal{A}, |
|
iii) |
nul-skup s obzirom na \mu ako i samo ako je \mu(A \cap F)=0, za svaki F \in \mathcal{A}. |
Dokaz ćemo provesti u slučaju ii), dok se ostali slučajevi dokazuju analogno.
Ukoliko pretpostavimo da je A \in \mathcal{A} negativan skup s obzirom na \mu i F \in \mathcal{A} proizvoljan, tada je skup A \cap F izmjeriv podskup od A te prema Propoziciji 15 vrijedi \mu(A \cap F) \leq 0.
Obratno, neka su A, E \in \mathcal{A} takvi da je je E \subseteq A te neka vrijedi \mu(A \cap F) \leq 0, za svaki F\in\mathcal{A}. Specijalno, za F=E dobivamo \mu(E)=\mu(A \cap E) \leq 0 iz čega slijedi da je A negativan skup s obzirom na \mu. \Box
Propozicija 17. Neka je
\mu mjera s predznakom na izmjerivom prostoru
(X, \mathcal{A}). Prebrojiva unija negativnih skupova je negativan skup. Specijalno, konačna unija negativnih skupova je negativan skup. Tvrdnje propozicije vrijede i za pozitivne i za nul–skupove.
Dokaz. Tvrdnju ćemo najprije dokazati u slučaju kada je dan prebrojiv niz (A_{n})_{n \in \mathbb{N}} negativnih skupova za \mu. U tu svrhu, neka je B izmjeriv podskup od \bigcup\limits_{n \in \mathbb{N}}A_{n} te bez smanjenja općenitosti možemo pretpostaviti da je B=\bigcup\limits_{n \in \mathbb{N}}B_{n}, gdje je (B_{n})_{n \in \mathbb{N}} niz disjunktnih skupova iz \mathcal{A} takvih da je B_{n} \subseteq A_{n}, za svaki n \in \mathbb{N}. Tada po Propoziciji 15 i \sigma-aditivnosti mjere s predznakom slijedi \mu(B)=\sum\limits_{n \in \mathbb{N}}\mu(B_{n}) \leq 0.
Specijalno, u slučaju kada imamo konačan niz A_{1},...,A_{n} negativnih skupova za \mu, možemo ga dopuniti do prebrojivog postavljanjem A_{m}=\emptyset, za svaki prirodni broj m\geq n+1. Ukoliko na takav nadopunjeni niz primjenimo prethodni dokaz, tvrdnja slijedi. \Box
Kao što smo najavili, Teorem 18 nam daje dekompoziciju skupa.
Teorem 18. [
Hahnova dekompozicija] Neka je
\mu mjera s predznakom na izmjerivom prostoru
(X, \mathcal{A}). Tada postoje dva izmjeriva skupa,
P i
N, takvi da je
P pozitivan, a
N negativan skup s obzirom na
\mu te
X=P\cup N i
P \cap N=\emptyset.
Dokaz ovog teorema je tehnički zahtjevniji, a svodi se na konstrukciju niza negativnih skupova koji vode do izmjerivnog negativnog skupa N te niza disjunktnih izmjerivih skupova koji, uz pomoć kontradikcije, vode do pozitivnog skupa P (vidi str. 124 iz [6], str. 25–27 iz [9]).
\Box
Napomena
Nije teško pokazati da Hahnova dekompozicija mjere s predznakom nije jedinstvena. Naime, ako su dane dvije Hahnove dekompozicije (P_{1},N_{1}) i (P_{2},N_{2}) mjere s predznakom \mu, na izmjerivom prostoru (X,\mathcal{A}), onda su prema Napomeni 15 skupovi N_{1}\cap P_{2} i N_{2}\cap P_{1} nul-skupovi za \mu. Iz jednakosti N_{1}\cap P_{2}=N_{1}\setminus N_{2} i N_{2}\cap P_{1}=N_{2}\setminus N_{1}, prema Propoziciji 17 slijedi da je
N_{1}\triangle N_{2}=(N_{1}\setminus N_{2})\cup(N_{2}\setminus N_{1})
nul–skup s obzirom na \mu. Analogno se pokaže i da je P_{1}\triangle P _{2} nul–skup s obzirom na \mu.
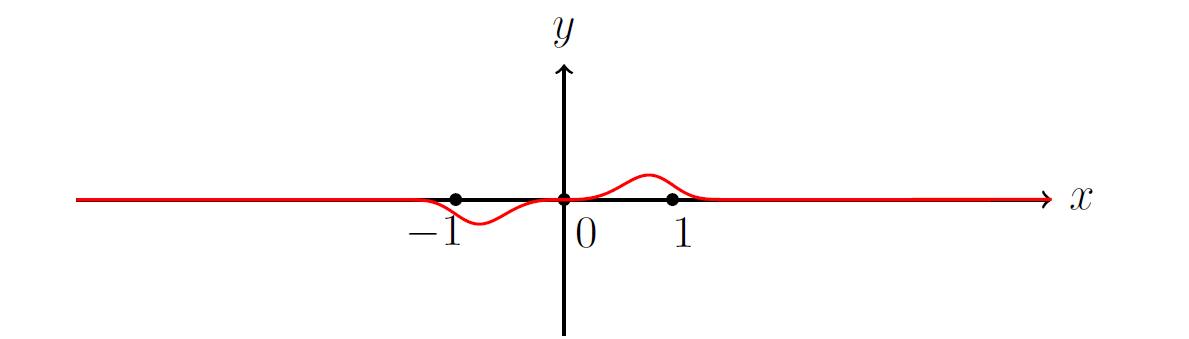
Primjer 19. Neka je
(\mathbb{R},\mathcal{B}(\mathbb{R}),\lambda) prostor mjere, gdje je
\lambda Lebesgueova mjera. Odredimo jednu Hahnovu dekompoziciju mjere s predznakom
\mu, zadane formulom
\begin{align*} \mu(E):=\int\limits_{E} x^{3} e^{-2 x^{4}}d\lambda,\hspace{5ex}E\in\mathcal{B}(\mathbb{R}). \end{align*}
Najprije uočimo da za danu funkciju
f(x)=x^{3} e^{-2 x^{4}} vrijedi
f(x) \geq 0 za
x \in [0, \infty \rangle i
f(x) \lt 0 za
x \in \langle -\infty, 0 \rangle (vidi Sliku 3). Prema
Primjeru 14 znamo da je
P=\lbrace x \in \mathbb{R}:f(x) \geq 0\rbrace pozitivan skup s obzirom na
\mu te da je
N=\lbrace \,x \in \mathbb{R}:f(x) \leq 0\,\rbrace negativan skup s obzirom na
\mu. Skup
N'=\lbrace x \in \mathbb{R}:f(x) \lt 0\rbrace je podskup od
N pa je i on negativan skup, prema
Propoziciji 15.
Graf funkcije \[f(x):=x^3 e^{-2 x^4}\].
Dakle, skupovi
P=[0, \infty \rangle i
N'=\langle -\infty, 0 \rangle su disjunktni i u uniji daju cijeli
\mathbb{R} pa je
(P,N') jedna Hahnova dekompozicija.
\blacksquare
Kao što smo i najavili, idući teorem, odnosno Jordanova dekompozicija, dat će nam alat pomoću kojeg ćemo zapisati mjeru s predznakom kao razliku dviju mjera. Pokazat će se, također, da je Jordanova dekompozicija mjere s predznakom jedinstvena.
Teorem 20. [
Jordanova dekompozicija] Neka je
\mu mjera s predznakom na izmjerivom prostoru
(X, \mathcal{A}). Tada postoje jedinstvene mjere
\mu^{+},\; \mu^{-}\colon\mathcal{A}\to[0,\infty] takve da je
\begin{align*} \mu=\mu^{+} - \mu^{-} \end{align*}
i pri tome je barem jedna od mjera
\mu^{+},\; \mu^{-} konačna.
Dokaz. Neka je s (P,N) dana Hahnova dekompozicija mjere s predznakom \mu te neka su funkcije \mu^{+}, \mu^{-}\colon \mathcal{A} \to [0, \infty] definirane za svaki E\in\mathcal{A} s
\begin{align*} \mu^{+}(E)&:=\mu(E\cap P), \qquad \mu^{-}(E):=-\mu(E\cap N). \end{align*}
Očito je da su \mu^{+} i \mu^{-} mjere s predznakom. Kako bismo dokazali da su \mu^{+} i \mu^{-} mjere, treba još provjeriti njihovu nenegativnost. Iz Teorema 16 zaključujemo
\mu^{+}(E)=\mu(E\cap P) \geq 0\,\,\text{ i}\,\,\, \mu^{-}(E)=-\mu(E\cap N)\geq 0,\,\,\text{ za svaki }\,\,E \in \mathcal{A}.
Mjere \mu^{+} i \mu^{-} su definirane preko mjere s predznakom \mu koja ne poprima istovremeno vrijednosti -\infty i +\infty, stoga je barem jedna od njih konačna.
Neka je E\in\mathcal{A}. Kako su P i N disjunktni te X=P \cup N, vrijedi
\begin{align*} \mu(E)=\mu(E \cap P) + \mu(E \cap N)=\mu^{+}(E)-\mu^{-}(E), \end{align*}
što je i trebalo pokazati. U nastavku preostaje dokazati jedinstvenost.
Neka su (P_{1},N_{1}) i (P_{2},N_{2}) dvije Hahnove dekompozicije mjere s predznakom \mu na izmjerivom prostoru (X,\mathcal{A}) te neka su mjere \mu_{1}^{+},\mu_{1}^{-},\mu_{2}^{+},\mu_{2}^{-}\colon\mathcal{A}\to[0,\infty] zadane s
\begin{align*} \mu_{1}^{+}(E)&=\mu(E\cap P_{1}),\qquad \mu_{1}^{-}(E)=-\mu(E\cap N_{1}),\\ \mu_{2}^{+}(E)&=\mu(E\cap P_{2}),\qquad \mu_{2}^{-}(E)=-\mu(E\cap N_{2}). \end{align*}
Skupovi P_{1}\setminus P_{2} i P_{2}\setminus P_{1} su, prema Napomeni 15, nul–skupovi za \mu. Tada za svaki E\in\mathcal{A} vrijedi
\begin{align*} \mu_{1}^{+}(E)&=\mu(E\cap P_{1})=\mu(E\cap((P_{1}\setminus P_{2})\cup(P_{1}\cap P_{2})))\\ &=\mu(E\cap(P_{1}\setminus P_{2}))+\mu(E\cap(P_{1}\cap P_{2}))=\mu(E\cap P_{2}\cap P_{1})+0\\ &=\mu(E\cap P_{2}\cap P_{1})+\mu(E\cap(P_{2}\setminus P_{1}))\\ &=\mu(E\cap((P_{2}\cap P_{1})\cup(P_{2}\setminus P_{1})))=\mu(E\cap P_{2})=\mu_{2}^{+}(E). \end{align*}
Analogno se pokaže da je \mu_{1}^{-}=\mu_{2}^{-}. \Box
Dakle, reprezentacija \mu=\mu^{+}-\mu^{-} mjere s predznakom \mu naziva se Jordanova dekompozicija mjere s predznakom \mu te također možemo uočiti da je \mu=\mu^{+} i \mu^{-}=0 u slučaju kada je \mu mjera, vidi str. 353 iz [21].
Korolar 21. Svaka realna mjera (konačna mjera s predznakom), na izmjerivom prostoru
(X, \mathcal{A}), je razlika dvije konačne mjere, na istom izmjerivom prostoru.
Dokaz je analogan dokazu Jordanove dekompozicije, vidi str. 109 iz [3]. \Box
Primjer 22. Odredimo Jordanovu dekompoziciju mjere s predznakom
\mu iz
Primjera 19.
Naime, u tom smo primjeru odredili jednu Hahnovu dekompoziciju
(P,N') mjere s predznakom
\mu, pri čemu je
P=[0, \infty \rangle i
N'=\langle -\infty, 0 \rangle. Tada je, očito, Jordanova dekompozicija dana s
\begin{align*} \mu^{+}(E)&:=\mu(E \cap P)=\int\limits_{E} f\chi^{}_{[0, \infty \rangle}\,d\lambda,\\ \\ \mu^{-}(E)&:=-\mu(E \cap N')=-\int\limits_{E} f\chi^{}_{\langle -\infty, 0 \rangle}\,d\lambda. \end{align*}
\blacksquare
Bibliografija
|
[1] |
E. H. Allen, Negative Probabilities and the Uses of Signed Probability Theory, Philosophy of Science, 43 (1976), 53–70. |
|
[2] |
G. de Barra , Measure Theory and Integration, 2\textsuperscript{nd} Edition, Woodhead Publishing, Cambridge, 2003. |
|
[3] |
H. Bauer , Measure and Integration Theory, Walter de Gruyter, Berlin, 2001. |
|
[4] |
M. Burgin, G. Meissner , Extended Correlations in Finance, Journal of Mathematical Finance, 6 (2016), 178–188. |
|
[5] |
M. Burgin, G. Meissner , Negative Probabilities in Financial Modeling, Wilmott Magazine, 58 (2012), 60–65. |
|
[6] |
D. L. Cohn, Measure Theory, Birkh{\"a}user, Boston, 1980. |
|
[7] |
P. A. M. Dirac , The Physical Interpretation of Quantum Mechanics, Proceedings of the Royal Society of London, 180 (1942), 1-39. |
|
[8] |
J. D. Enderle, D. C. Farden, D. J. Krause, Basic Probability Theory for Biomedical Engineers, Morgan & Claypool Publishers, 2006.
URL: https://doi.org/10.2200/S00037ED1V01Y200606BME005 |
|
[9] |
A. Friedman, Foundations of Modern Analysis, Dover, New York, 1982. |
|
[10] |
R. Feynman Negative Probability. In: Hiley, B.J. and Peat, F., Eds., Quantum Implications: Essays in Honour of David Bohm, Routledge & Kegan Paul Ltd., London and New York, 235-248, 1987. |
|
[11] |
H. Hahn , Theorie der reellen Funktionen, Springer–Verlag, Berlin, 1921. |
|
[12] |
P. R. Halmos , Measure Theory, Springer-Verlag, New York, 1974. |
|
[13] |
E. G. Haug , The Collector: Why So Negative to Negative Probabilities?, Wilmott Magazine, (2004) 34–38. |
|
[14] |
D. Jukić, Mjera i integral, Sveučilište J. J. Strossmayera, Odjel za matematiku, Osijek, 2012. |
|
[15] |
D. Jankov Maširević, Zbirka riješenih zadataka iz teorije mjere i integracije, Sveučilište J. J. Strossmayera, Odjel za matematiku, Osijek, 2014. |
|
[16] |
R. Kaas, M. Goovaerts, J. Dhaene, M. Denuit , Modern Actuarial Risk Theory: Using R, 2\textsuperscript{nd} Edition, Wiley, New York, 2009. |
|
[17] |
L. H. Koopmans, Teaching Singular Distributions to Undergraduates, The American Statistician, 37 (1983), 313–316.
URL: https://www.jstor.org/stable/2682772 |
|
[18] |
T. Marković , Dekompozicija mjere, diplomski rad, Sveučilište J. J. Strossmayera, Odjel za matematiku, Osijek, 2019. |
|
[19] |
M. Pivato, Analysis, Measure, and Probability: A visual introduction, Mexico McGraw-Hill, Mexico, 2003. |
|
[20] |
J. J. Shynk, Probability, Random Variables, and Random Processes: Theory and Signal Processing Applications, Wiley, Hoboken, New Jersey, 2013. |
|
[21] |
A. E. Taylor, General Theory of Functions and Integration, Blaisdell Publishing Company, Waltham, 1966. |
|
[22] |
J. Yeh, Real Analysis, Theory of Measure and Integration, 2\textsuperscript{nd} Edition, University of California, Irvine, 2006. |
|
[23] |
E. P. Wigner, On the Quantum Correction for Thermodynamic Equilibrium, Physics Review, 40 (1932), 749–759. |