Kvazislučajni brojevi i numerička integracija
Stavimo pred čitatelja poznato trik-pitanje koje provjerava naše poimanje “slučajnosti”.
| \bullet |
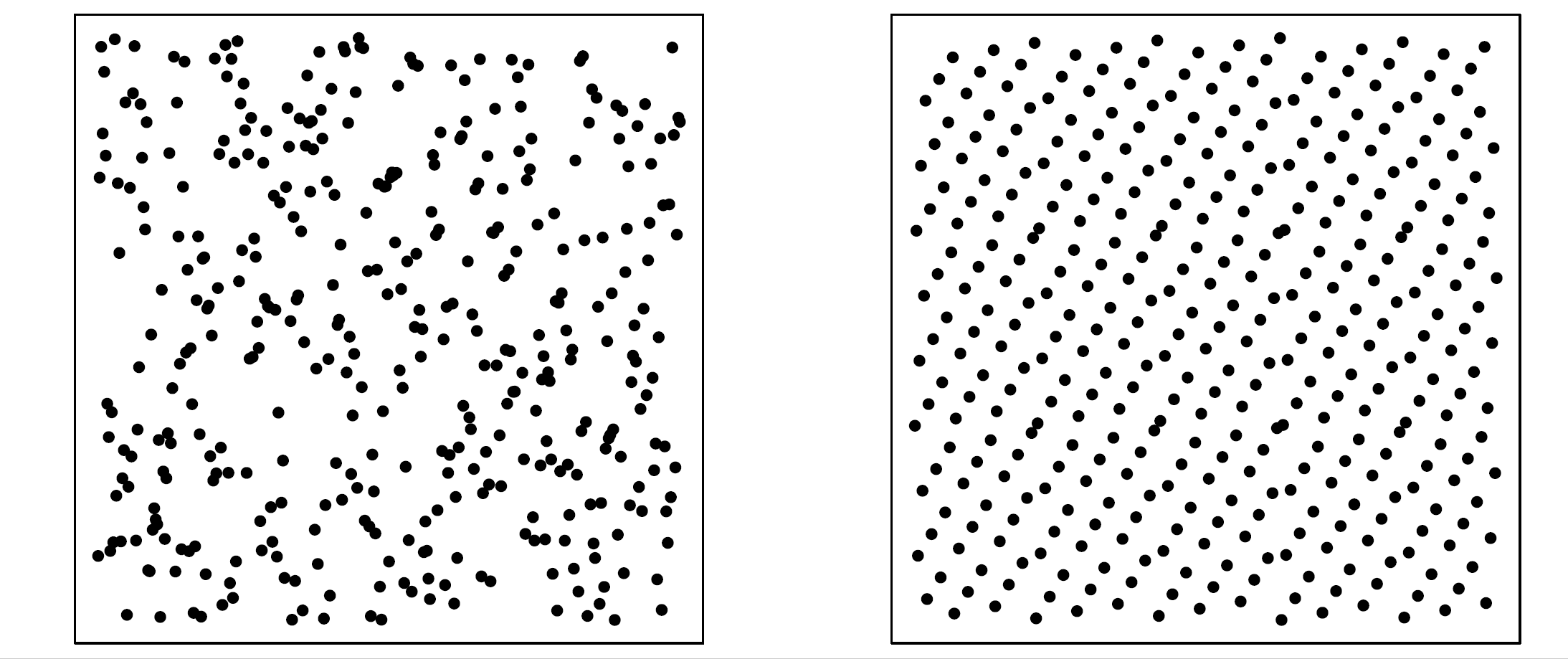
Koji od kvadrata na slici |
Lako može zavesti činjenica da lijevi kvadrat sadrži i nakupine točaka i praznine, a to je nešto što neiskusni čitatelj možda ne očekuje od slučajnog niza. Zavarati može i činjenica da točke u desnom kvadratu ravnomjerno ispunjavaju njegovu površinu, što bismo mogli dovesti u vezu s činjenicom da u svaki djelić kvadrata slučajno odabrana točka pada s jednakom vjerojatnosti. Oba ta argumenta, koji navode na odgovor “desni kvadrat”, su pogrešni! Kod slučajno generiranog niza točaka s velikom vjerojatnosti se formiraju razne praznine i nakupine, dok s malom vjerojatnosti on baš ravnomjerno počinje ispunjavati kvadrat. Radi toga je “lijevi kvadrat” točniji odgovor, u smislu da nam simulacija slučajnog niza točaka vrlo vjerojatno izgleda baš kao na lijevoj polovici slike.
Ako smo pak sasvim rigorozni, onda je prethodno pitanje besmisleno! S teorijskog stanovišta oba scenarija na slici
čitatelj je zasigurno upoznat s pojmom integrala funkcije, makar na intuitivnom nivou. Integral (tj. određeni integral) dovoljno “lijepe” (recimo neprekidne) funkcije f\colon[a,b]\to\mathbb{R} je broj pisan
a kojeg se interpretira kao površinu ispod grafa funkcije, a iznad apscise. Pritom se površina uzima s negativnim predznakom tamo gdje je funkcija negativna. Osnove diferencijalnog i integralnog računa te, posebno, rigoroznu definiciju tzv. Riemannovog integrala čitatelj može naći u knjigama
U srži numeričkog računanja integrala leži njegova aproksimacija diskretnim sumama, a najjednostavniji slučaj je
pri čemu za točke x_{n}\in[0,1], n=1,2,\ldots,N, možemo uzeti recimo x_{n}=(n-1)/N ili x_{n}=n/N pa dobivamo tzv. lijevu i desnu pravokutnu formulu. Za svaki od ta dva izbora greška aproksimacije (
Greška aproksimacije (
Kod višestrukog integrala, \int_{[0,1]^{d}}f, tj. integrala d-dimenzionalne funkcije f\colon[0,1]^{d}\to\mathbb{R}, postupamo slično. U svakoj koordinati možemo promatrati točke 0,1/M,2/M,\ldots,(M-1)/M pa onda za čvorove x_{n} u d-dimenzionalnom poopćenju lijeve pravokutne formule uzimamo sve različite d-torke tih brojeva; ima ih N=M^{d}. Usrednjivanjem se dobiva i d-dimenzionalna trapezna formula čija greška je reda veličine M^{-2}=N^{-2/d}, čim funkcija ima neprekidne sve druge parcijalne derivacije.
Postoje i mnogo naprednije metode numeričke integracije od navedenih; pogledajte skriptu
Nedostatak 1. Sve klasične formule se u velikom broju dimenzija susreću s tzv. kletvom dimenzionalnosti. Npr. ako je teorijska greška aproksimacije C N^{-2/d}, a želimo garantirati preciznost \varepsilon, tada treba uzeti N\geq (C/\varepsilon)^{d/2}, tj.broj čvorova u kojima se funkcija treba izračunati raste eksponencijalno s povećanjem dimenzije d. Poteškoću možemo vidjeti već i zdravo-razumski: ako u d=100 dimenzija želimo imati bilo kakvu razumnu aproksimaciju, onda kod gornjih aproksimacija u svakoj koordinati moramo uzeti barem po dvije točke (a i to je vrlo skromno), što nas vodi na ukupno 2^{100}\approx 1.27\cdot10^{30} čvorova — definitivno previše za bilo koje računalo!
Nedostatak 2. Klasične metode pretpostavljaju izvjesnu glatkoću funkcije koja se integrira. Sofisticiranije formule daju bolju grešku aproksimacije, ali i pretpostavljaju povećanu glatkoću; npr. poznata Simpsonova formula u jednoj dimenziji ima teorijsku grešku reda veličine C(f^{(4)}) N^{-4} — ona je reda veličine N^{-4}, ali uz pretpostavku ograničenosti četvrte derivacije funkcije f.
Nedostatak 3. Numerička integracija može iziskivati računanje funkcije f u velikom broju čvorova x_{n}, a to može biti vrlo spor proces ukoliko je funkcija složena. Ponekad nas zahtjev za greškom manjom od \varepsilon vodi na veći broj računskih operacija nego ih računalo može podnijeti u danom vremenu. Zato bismo voljeli imati aproksimacijski algoritam kojeg možemo zaustaviti nakon bilo kojeg broja obrađenih čvorova. Uočimo da gore spomenute formule za numeričku integraciju nemaju to svojstvo; ako zaustavimo računanje trapezne formule (
Postoji tehnika numeričke integracije koja zaobilazi sva tri spomenuta nedostatka i zove se Monte Carlo metoda. Kod nje su čvorovi x_{n} slučajni brojevi iz intervala [0,1] ili pak slučajne točke iz d-dimenzionalne kocke [0,1]^{d}. U teoriji je x_{1}, x_{2}, x_{3}, \ldots niz nezavisnih slučajnih varijabli iz intervala [0,1]. Kvadratni prosjek greške aproksimacije integrala je tada oblika C(f) N^{-1/2}, pri čemu je konstanta C(f) konačna već kada |f|^{2} samo ima konačan integral; vidjeti
Jedno od prvih elektroničkih računala, imena ENIAC, dovršeno je 1945. godine. Već je iduće godine poznati poljsko-američki matematičar Stanis{\l}aw Ulam došao na ideju da iskoristi njegovu brzinu za Monte Carlo simulacije vezane uz razne fizikalne probleme, a posebno one vezane uz razvoj nuklearnog oružja u laboratoriju u Los Alamosu. Ništa manje slavni, mađarsko-američki matematičar John von Neumann je, nadahnut idejom svojeg kolege, već 1947. razradio plan implementacije te metode na računalo ENIAC; detalji te priče mogu se pročitati u popularnom članku
Monte Carlo metoda pak ima neke svoje nedostatke.
Nedostatak 4. Za implementaciju te tehnike treba generirati niz slučajnih brojeva, tj. savršeno simulirati niz nezavisnih slučajnih varijabli. U praksi to nikada nije moguće! Von Neumann je prilikom svoje implementacije Monte Carlo metode za ENIAC opisao neke moguće konstrukcije pseudoslučajnih brojeva. Oni su deterministički generirani, ali po mnogim statističkim svojstvima imitiraju slučajnost. Ipak, tada postoji opasnost od nesrazmjera teorijske pozadine i praktične realizacije. Konkretnim problemom simulacije slučajnih varijabli se ovdje nećemo baviti, jer je on težak već sam za sebe.
Nedostatak 5. Monte Carlo metoda u praksi dosta sporo konvergira. To vidimo već i iz ocjene greške oblika C(f) N^{-1/2}; ona je inferiorna naspram greškama ranije spomenutih determinističkih metoda, koje su redom reda veličina N^{-1}, N^{-2}, odnosno čak N^{-4}. To nas ne treba čuditi jer ona ne uspijeva iskoristiti informaciju o mogućoj dodatnoj glatkoći zadane funkcije f — algoritam uvijek postupa jednako, što je s jedne strane njegova prednost, a s druge strane njegova mana.
Nedostatak 6. Spomenuta ocjena greške je vjerojatnosna, tj. ne možemo baš ništa zaključiti o greški aproksimacije dobivene pomoću neke konkretne simulacije niza slučajnih varijabli. Kako možemo znati da naša simulacija neće započeti baš s tisuću nula? U tom slučaju izraz s desne strane od
Tehnika koju ćemo sada opisati zove se kvazi Monte Carlo metoda i ona stoji na pola puta između pristupa iz prethodna dva odjeljka: deterministička je, ali po mnogo čemu imitira Monte Carlo metodu. Ona nipošto nije univerzalno rješenje problema numeričke integracije, već naprosto vrlo dobar kompromis između nedostataka 1–6 prethodnih metoda.
Glavna ideja kvazi Monte Carlo metode je uzeti čvorove x_{n} koji će naizgled dobro oponašati slučajne, na način da će ravnomjerno popunjavati prostor. Pokazat će se da će takvi čvorovi davati povoljnu numeričku aproksimaciju integrala, uz dodatno dobro svojstvo determiniranosti. Tu ćemo ideju sada i formalizirati. Uglavnom ćemo se zadržati u dimenziji d=1.
Neka je \textbf{x}=(x_{n})_{n=1}^{\infty} proizvoljan niz brojeva iz intervala [0,1]. Za skup S \subseteq [0,1] i broj N\in\mathbb{N} definiramo tzv. brojeću funkciju kao
Riječima, između prvih N članova niza \textbf{x} njih točno \text{Br}_{N}(\textbf{x},S) se nalazi u skupu S. Reći ćemo da je niz \textbf{x} ekvidistribuiran3 ako za svaki interval I\subseteq[0,1] vrijedi
Kakve veze ima pojam ekvidistribuiranosti s računanjem integrala funkcije? Pokazuje se da za ekvidistribuirani niz \textbf{x} brojeva iz [0,1] i za Riemann-integrabilnu funkciju f\colon[0,1]\to\mathbb{R} uvijek vrijedi
Dakle, integral funkcije je prikazan kao limes niza konačnih suma, prosjeka funkcije u prvih N članova niza \textbf{x}. Formula
Za niz \textbf{x}=(x_{n})_{n=1}^{\infty} brojeva iz intervala [0,1] i prirodni broj N definiramo diskrepanciju od \textbf{x} kao broj
pri čemu se supremum uzima po svim intervalima I\subseteq[0,1]. što je diskrepancija manja, to su točke ravnomjernije raspoređene.
Kako se sada povezuje diskrepancija niza \textbf{x} s aproksimacijom integrala zasnovanom na formuli
pri čemu se supremum uzima po svim m\in\mathbb{N} i svim mogućim izborima brojeva a_{0},a_{1},\ldots,a_{m-1},a_{m} takvih da je 0\leq a_{0}\lt a_{1}\lt \cdots\lt a_{m}\leq 1. Zanimaju nas funkcije za koje je \text{V}(f)\lt \infty; npr. sve neprekidno diferencijabilne funkcije su takve. Koksma je prvi dokazao nejednakost
koja eksplicitno ocjenjuje grešku prethodno spomenute aproksimacije integrala. Iz
Sa druge strane, u idućem ćemo odjeljku navesti neke primjere nizova \textbf{x} takvih da za svaki N\in\mathbb{N} vrijedi
uz neku konstantu C ovisnu o nizu \textbf{x}.
Vrlo slično definiraju se ekvidistribuiranost i diskrepancija niza točaka u d-dimenzionalnoj kocki [0,1]^{d} za d\geq 2. Poznata otvorena slutnja glasi da postoji konstanta c\gt 0, ovisna samo o dimenziji d, takva da za svaki niz točaka \textbf{x} iz [0,1]^{d} možemo naći beskonačno mnogo N\in\mathbb{N} za koje vrijedi
Osim za d=1 ta slutnja je još jedino provjerena u d=2 dimenzije. Svi navedeni jednodimenzionalni rezultati također imaju i svoje višedimenzionalne analogone. Detalje čitatelj može naći u knjizi
Kvazislučajan niz brojeva iz [0,1] ili točaka iz [0,1]^{d} nam od sada naprosto znači niz s niskom diskrepancijom. Na osnovu rečenog pod time se obično misli niz \textbf{x} takav da za svaki N\in\mathbb{N} vrijedi
uz neku konstantu C. To se doista i može postići i to raznolikim konstrukcijama, od kojih ćemo neke navesti u nastavku.
čitatelj sada već pogađa: Kvazi Monte Carlo metoda aproksimira integral tako da na desnoj strani formule
Nakon što smo uvidjeli korisnost nizova s niskom diskrepancijom, prirodno se pitamo kako generirati takve nizove. Opišimo dvije klasične konstrukcije.
Proizvoljan prirodni broj n ima jedinstveni raspis u bazi b\geq 2 oblika
gdje su a_{j}(n)\in \lbrace 0,1,\ldots,b-1\rbrace njegove znamenke i a_{j}(n)=0 za sve dovoljno velike indekse j; odnosno gornja suma je zapravo konačna. Sada, tzv. obrtanjem znamenaka, za svaki n možemo definirati broj
koji pripada jediničnom intervalu [0,1]. Za danu bazu b\geq2 van der Corputov niz je upravo niz brojeva x_{0}, x_{1},\ldots definiran sa x_{n}=\phi_{b}(n) za sve n\in\mathbb{N} i on je primjer niza čija diskrepancija zadovoljava
Računalno praktičan način dobivanja višedimenzionalnih nizova niske diskrepancije je generalizacija van der Corputovog niza. Koristeći netom uvedenu funkciju \phi_{b} Haltonov niz u bazama b_{1},\ldots,b_{d}\geq2 definiramo kao niz točaka x_{0}, x_{1}, \ldots iz [0,1]^{d} takav da vrijedi
Ukoliko su brojevi b_{1},\ldots,b_{d} relativno prosti, tada gornji niz zadovoljava
Ukoliko samo želimo kvadrat [0,1]^{2} ravnomjerno ispuniti unaprijed zadanim brojem točaka N, možemo koristiti i tzv. Hammersleyev skup za bazu b\geq 2:
Naprimjer, desna polovica slike
Za proizvoljan broj u\in \mathbb{R} definiramo decimalni dio broja u kao \lbrace u\rbrace :=u-\lfloor u\rfloor. Drugim riječima, za nenegativan u, imamo da je \lbrace u\rbrace dio zapisa od u koji se nalazi iza decimalne točke. Niz niske diskrepancije \textbf{x}=(x_{n})_{n=1}^{\infty} tada dobijemo promatranjem decimalnih dijelova višekratnika fiksiranog iracionalnog broja z, odnosno možemo definirati x_{n}=\lbrace nz\rbrace za sve n\in\mathbb{N}. Svaki tako definiran niz brojeva \textbf{x} je ekvidistribuiran. Ipak, ako inzistiramo na optimalnoj ocjeni za diskrepanciju
Slično možemo dobiti višedimenzionalne nizove niske diskrepancije. Neka je z=(z_{1},\ldots,z_{d})\in\mathbb{R}^{d} takav da su brojevi 1,z_{1},\ldots,z_{d} linearno nezavisni nad racionalnim brojevima, tj.
i neka je niz točaka x_{0},x_{1},\ldots definiran sa
Takav niz točaka je uvijek makar ekvidistribuiran, ali mu ocjena diskrepancije vodi na ozbiljne probleme u području teorije brojeva.
Pokušajmo numerički izračunati određeni integral
Radi usporedbe s pravom vrijednosti odabrali smo integral kojeg znamo i egzakno izračunati: parcijalnom integracijom lako dobivamo
U svrhu primjene gornjih metoda najprije integral
Za funkciju f zadanu formulom f(t)=(t+3) e^{t+3} koristili smo Monte Carlo metodu i kvazi Monte Carlo metodu uz van der Corputov niz za bazu b=3. Usporedni numerički rezultati dani su tablicama na slici
| N | 10 | 100 | 1000 | 100000 |
| num. rezultat | 120.5889 | 124.4008 | 122.4759 | 123.4507 |
| rel. odstupanje | 2.45\% | 0.63\% | 0.93\% | 0.14\% |
| N | 10 | 100 | 1000 | 100000 |
| num. rezultat | 113.6413 | 121.7685 | 123.3847 | 123.6190 |
| rel. odstupanje | 8.07\% | 1.50\% | 0.19\% | 0.004\% |
Integrali su jedan od osnovnih matematičkih pojmova s brojnim primjenama, kako unutar, tako i izvan same matematike. česte su situacije kada je integral nepraktično, a ponekad i nemoguće egzaktno izračunati. U takvim je slučajevima korisno poslužiti se metodama numeričke integracije, odnosno numeričkom aproksimacijom integrala u pitanju, za što postoje brojne klasične metode (trapezna formula, Simpsonova formula, itd.). Takve metode, uz brojne prednosti, posjeduju i neke spomenute mane.
Bitno različit postupak, koji predstavlja poboljšanje u odnosu na neke klasične nedostatke, je Monte Carlo metoda, odnosno korištenje slučajno generiranih točaka pri procjeni integrala. Monte Carlo metoda, uz broj čvorova N, daje grešku aproksimacije reda veličine N^{-\frac{1}{2}}, što je lošije od klasičnih metoda, ali je neovisno od broja dimenzija d. Kvazi Monte Carlo metoda je determinističko poboljšanje Monte Carlo metode koje uspijeva zadržati neke njezine prednosti. U njoj se koristimo kvazislučajnim nizovima, odnosno nizovima niske diskrepancije, za koje smo neke od klasičnih konstrukcija dali u ovome radu.
Već smo bili komentirali da kvazi Monte Carlo metoda ima grešku oblika C N^{-1}(\log N)^{d}, koja je asimptotski (tj. kada N\to\infty) bolja od C N^{-1/2}, što je pak greška Monte Carlo metode. Ipak, za konkretni neveliki N i za visoki broj dimenzija d na temelju ocjena grešaka očekujemo da će kvazi Monte Carlo metoda sporije konvergirati od Monte Carlo metode. U praksi se pokazalo da nije nužno tako. Jedna od tipičnih primjena kvazi Monte Carlo metode je u financijama, gdje su integrali u d=100 ili d=1000 varijabli sasvim uobičajeni. Godine 1995. Paskov i Traub su u radu