Birch i Swinnerton-Dyerova slutnja
Skup rješenja polinomijalne jednadžbe
definira krivulju C. Ako su koeficijenti polinoma f racionalni brojevi postavlja se pitanje koje su racionalne točke na krivulji, tj. rješenja jednadžbe
Skup racionalnih točaka krivulje označavamo s C(\mathbb{Q}).
Zanima nas odgovor na pitanje: Koliko je velik C(\mathbb{Q})? Je li beskonačan?
Napomenimo da poljem algebarskih brojeva nazivamo konačno proširenje polja \mathbb{Q}.
[Tm. VIII.4.1, 6]
Diofantske jednadžbe. U vezi gornjeg, diofantske jednadžbe možemo podijeliti u tri klase:
| \bullet | racionalne, |
| \bullet | eliptičke, |
| \bullet | općeg tipa. |
Grubo govoreći one korespondiraju jednadžbama stupnja 2,3 i \ge 4, respektivno.
Pokazuje se da je problem nalaženja racionalnih rješenja:
| \bullet | lagan za prvu klasu, |
| \bullet | težak ali napadljiv za drugu, |
| \bullet | općenito nemoguć za treću. |
Preciznije:
Racionalne jednadžbe ukoliko imaju jedno, automatski imaju beskonačno mnogo rješenja i postoji formula koja ih sve daje.
Eliptičke jednadžbe mogu imati konačno ili beskonačno mnogo rje\v senja. Međutim, imamo lijepu teoriju koja opisuje strukturu rješenja, te daje način kako provjeriti ima li ih konačno ili beskonačno mnogo \v sto je upravo dano sa slutnjom Birch i Swinnerton-Dyera.
Jednadžbe općeg tipa imaju najviše konačno mnogo rješenja (slutnja Mordell 1917., dokaz Faltings 1984.). Općenito ne postoji algoritam za nalaženje tih rješenja.
Za bilo koju točku P\in E(\mathbb{K}) kažemo da je racionalna.
Grupa divizora na krivulji C (vidi
gdje je n_{P}\in \mathbb{Z} te je n_{P}=0 za sve osim konačno mnogo P\in C. Stupanj od D definira se kao
Za projektivnu krivulju C nad poljem \mathbb{K} s \mathbb{K}(C) označavamo polje racionalnih funkcija na krivulji C, dok s \mathbb{K}(C)^{\times} pripadnu multiplikativnu grupu, tj. grupu svih nenul elemenata od \mathbb{K}(C) s operacijom množenja (vidi
Skup L(D) je vektorski potprostor nad K od K(C). Definiramo
Riemann-Rochov teorem. Jedna posljedica Riemann-Rochovog teorema je:
Neka je P\in C(K). Slijedi da je \ell(nP)=n. Iz toga dobijemo rastući niz potprostora
Kako je \ell(2P)=2 i K=L(P)\subset L(2P) slijedi da postoji funkcija x koja ima pol reda 2 u P i nema niti jedan drugi pol. Analogno postoji funkcija y koja u P ima točno pol reda 3 i nema niti jedan drugi pol.
Kako su funkcije s različitim redom pola u P linearno nezavisne, pomoću x i y možemo dobiti baze za različite prostore L(nP):
Na isti način u prostoru L(6P) dobijemo 7 funkcija
Kako je \dim L(6P)=6 one moraju biti linearno zavisne.
Weierstrassova forma. Iz toga dobijemo da je krivulja C izomorfna glatkoj projektivnoj krivulji oblika
gdje su a_{i}\in K. Ovaj izomorfizam šalje točku P\mapsto \mathcal{O} =(0:1:0), tj. u točku u \infty. Gornju jednadžbu nazivamo Weierstrassova forma za eliptičku krivulju E. Afina verzija jednadžbe je
Ako je \text{char}(K)\ne 2,3 zamjenom varijabli možemo eliptičku krivulju zapisati u kratkoj Weierstrassovoj formi
Ako je eliptička krivulja dana u kratkoj Weierstrassovoj formi tada se vrijednost
naziva diskriminanta eliptičke krivulje. Vrijedi da je eliptička krivulja glatka (nesingulara) ako i samo ako je \Delta(E)\ne 0.
Grupovni zakon.
Po Mordell-Weilovom teoremu i klasifikaciji konačno generiranih Abelovih grupa slijedi
Ovdje je T je podgrupa elemenata konačnog reda koju zovemo torzijska podgrupa, dok je r\ge 0 i naziva se rang od E(K). Torzijsku podgrupu označavamo s E(\mathbb{K})_{tors}.
Rang.
Za konkretnu eliptičku krivulju, torziju je lako izračunati.
O rangu (nad \mathbb{Q}) se puno manje zna. Ne zna se niti može li biti proizvoljno velik ili postoji gornja ograda za rang svih eliptičkih krivulja nad \mathbb{Q}.
Najveći poznati rang eliptičke krivulje nad \mathbb{Q} je 28 (Elkies 2006).
Želimo smisleno računati prosječni rang. Za to moramo nekako moći brojati eliptičke krivulje E nad \mathbb{Q}. U tu svrhu se uvodi funkcija visine H(E) na skupu svih racionalnih eliptičkih krivulja E/\mathbb{Q}, koju mi nećemo precizno definirati. Pokazuje se da je za bilo koji X\in \mathbb{R} broj eliptičkih krivulja E/\mathbb{Q} takvih da je H(E)\le X konačan. Ova činjenica nam omogućava da definiramo prosječni rang kao limes (ako postoji):
Kongruentni brojevi.
Veza eliptičkih krivulja s kongruentnim brojevima je u slijedećoj činjenici:
Birch i Swinnerton-Dyerova slutnja je dobila ime po matematičarima Bryanu Birchu i Peteru Swinnerton-Dyeru koji su do slutnje došli tijekom prve polovice 1960-ih uz pomoć računala.
Bryan John Birch (rođen 25. rujna 1931.) je britanski matematičar s Matematičkog instituta Sveučilišta u Oxfordu. Doktorirao je na Sveučilištu u Cambridgeu.
Sir Henry Peter Francis Swinnerton-Dyer (2. kolovoza 1927. - 26. prosinca 2018.) bio je engleski matematičar specijaliziran za teoriju brojeva na Sveučilištu u Cambridgeu.
BSD slutnja se odnosi na veličinu ranga. Konkretno ona kaže da je (algebarski) rang jednak analitičkom koji se definira preko tzv. L-funkcija. Osnovna ideja je brojati točke nad konačnim poljima. Za to nam je ključna sljedeća procjena:
Neka je N_{p}=\# E(\mathbb{F}_{p}) i označimo grešku gornje procjene s a_{p}
Neka je C singularna kubika nad poljem \mathbb{K} i neka je karakteristika polja različita od 2 i 3. Tada možemo napraviti zamjenu koordinata takvu da jednadžba od C ima oblik
Ako smo redukcijom modulo p neke eliptičke krivulje E/\mathbb{Q} dobili singularnu kubiku C tada kažemo da
Zanima nas N_{p} broj točaka singularne kubike nad \mathbb{F}_{p} kao i koeficijenti greške a_{p}=p-N_{p}. Definicija od a_{p} se razlikuje od one za eliptičke krivulje jer smo eliminirali singularnu točku iz razmatranja. Imamo sljedeću tablicu
| Tip redukcije | N_{p} | a_{p} |
| Aditivna | p | 0 |
| Rascijepiva multiplikativna | p-1 | 1 |
| Nerascijepiva multiplikativna | p+1 | -1 |
Vidimo da se broj točaka singularne kubike nad konačnim poljem automatski dobije iz tipa redukcije. Međutim, broj točaka eliptičke krivulje nad \mathbb{F}_{p} je mnogo suptilnija stvar.
Redukcija modulo p inducira homomorfizam grupa
Hasseov teorem nam kaže
iz čega zaključujemo da
bez obzira je li E(\mathbb{Q}) konačan ili beskonačan.
Birch i Swinnerton-Dyer su primjetili da ukoliko je E(\mathbb{Q}) beskonačan, tada broj točaka u E(\mathbb{F}_{p}) ima tendenciju biti veći nego što je to uobičajeno.
Ideja je mjeriti prosječnu veličinu od N_{p}=|E(\mathbb{F}_{p})|.
Stoga normaliziramo promatrajući \frac{N_{p}}{p} umjesto N_{p}.
Vrijedi
Dakle \frac{N_{p}}{p}\approx 1 i \lim\limits_{n\to\infty}\frac{N_{p}}{p} =1.
Međutim, ovo vrijedi za bilo koju eliptičku krivulju pa nam to ne daje neku korisnu informaciju.
Birch Swinnerton-Dyer-ova ideja bila je gledati parcijalne produkte N_{p}/p-ova i vidjeti koliko brzo oni postaju veliki. Definirajmo funkciju
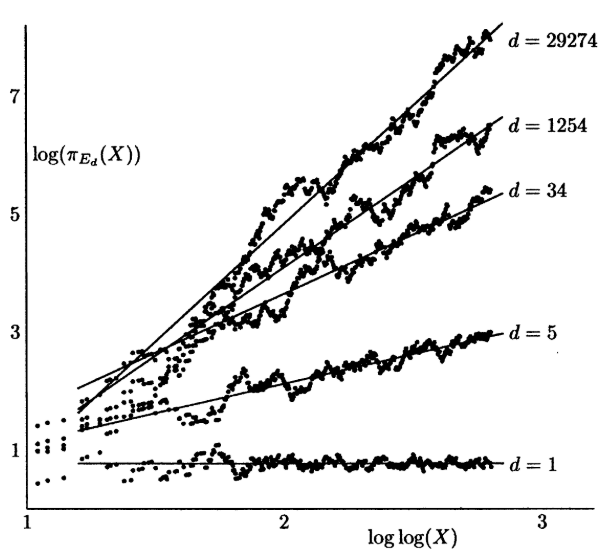
Kako bi testirali svoju ideju Birch i Swinnerton-Dyer su 1960. god. računali \pi_{E}(X) kada X raste za određene eliptičke krivulje E.
BSD eksperiment.
Slika pokazuje ponašanje od \pi_{E_{d}}(X) za X-eve do 1.5 \times 10^{7} za pet različitih krivulja E_{d} \colon y^{2}=x^{3}-d^{2}x koje redom imaju rang 0, 1, 2, 3 i 4.
Iz slike se uočava približna linearna ovisnost veličine \log(\pi_{E}(X)) o veličini \log(\log(X)) tj.
Uz C'=\log(C) Birch i Swinerton-Dyer su inicijalno naslutili da
kada X\to\infty za neku konstantu C koja ovisi samo o E.
Međutim funkcija \pi_{E} se ne ponaša jako lijepo i s njom je teško raditi. Stoga su Birch i Swinnerton-Dyer postavili srodnu slutnju koristeći L-funkciju od E umjesto funkcije \pi_{E}.
L-funkcije.
L-funkcija od E je Eulerov produkt
gdje je a_{p}=p+1-N_{p} za dobru redukciju, a za lošu redukciju imamo vrijednosi iz tablice
Kako bi vidjeli vezu L_{E} funkcije s funkcijom \pi_{E}, uvrstimo s=1 (iako tu L_{E} ne konvergira) u produkt i zanemarimo konačno mnogo loših prostih brojeva:
Ocjena |a_{p}|\lt 2\sqrt{p} (Hasse) povlači da gornji produkt konvergira za \Re(s)\gt 3/2.
Svaki dobar faktor se može razviti u obliku reda
gdje je a_{p} na lijevoj strani jednak a_{p} na desnoj (pa to nije loša notacija), te vrijedi
Za p-ove loše redukcije stavimo a_{p^{k}}=a_{p}^{k}. Tada produkt po svim p-ovima daje izraz
Gore je za n=\prod_{j}p_{j}^{e_{j}}
Ovaj red za L_{E}(s) konvergira za \Re(s)\gt 3/2.
Prirodno je pitati se ima li L_{E}(s) analitičko produljenje na cijeli \mathbb{C} te zadovoljava li neku funkcijsku jednadžbu, kao što je to slu\v caj s Riemannovom zeta funkcijom (vidi
Odgovor na to pitanje je pozitivan i dan je s Teoremom modularnosti.
Teorem modularnosti - (ex. Taniyama–Shimurina slutnja).
Kako bi se proučavala analitička svojstva od L_{E}(s) uvodimo novu funkciju. Neka je \tau\in\mathbb{H}, gdje je \mathbb{H} gornja poluravnina i neka je q=e^{2\pi i \tau} \, (=e^{2\pi(-y+ix)}\, ). Definiramo
Ovo je funkcija izvodnica koja kodira brojeve točaka na E modulo bilo koji prost broj. Njen red konvergira za \tau\in \mathbb{H} i zadovoljava neka fascinantna svojstva.
Za bilo koji prirodan broj N definiramo podgrupu od SL_{2}(\mathbb{Z}), u oznaci \Gamma = \Gamma_{0}(N) na slijedeći način
| (1) |
f_{E}\left(\frac{a\tau+b}{c\tau+d}\right)=(cz+d)^{2} f_{E}(\tau) \ \ \text{za sve} \ \gamma = \left( \begin{matrix} a & b \\ c & d \end{matrix}\right)\in \Gamma_{0}(N)
|
| (2) |
f_{E}(-1/(N\tau)) = \pm N\tau^{2} f_{E}(\tau).
|
Drugim riječima: Holomorfna funkcija f_{E}(\tau) je primitivna cusp forma težine 2 za \Gamma_{0}(N).
Ovaj teorem (uz tvrdnje o ponašanju u kaspovima na realnoj osi) kaže da je f_{E}(\tau) modularna forma (u stvari kusp formna) težine 2 i nivoa N. Najmanji mogući takav N naziva se konduktor od E. Prost broj p dijeli N ako i samo ako E ima lošu redukciju u p.
Teorem modularnosti povlači slijedeći rezultat koji je dugo bio poznat kao Hasse-Weilova slutnja. [Kor. 14.5,8], [Tm. 5.4, 5].
Tada funkcija
Analitičko produljenje od L_{E}(s). Gornji teorem automatski povlači da i funkcija L_{E}(s) ima analitičko produljenje na cijeli \mathbb{C}; uočimo da je \left(\frac{\sqrt{N}}{2\pi}\right)^{s} \cdot \Gamma(s) različito od 0 za svaki s\in \mathbb{C}. Sjetimo se da je funkcija L_{E}(s) inicijalno definirana redom, konvergirala samo za \Re(s)\gt 3/2.
Kako je L_{E}(s) analitička funkcija na cijelom \mathbb{C} možemo je razviti u Taylorov red oko s=1, tj.
tako da je r_{an}\ge 0 i c_{r_{an}}\ne 0. Nenegativan cijeli broj r_{an} nazivamo analitički rang.
| \bullet | \tilde{L}_{E}(s) - kodira informacije o E(\mathbb{F}_{p}) za sve osim konačno mnogo ("loših") prostih brojeva p, |
| \bullet | L_{E}(s) - uključuje informacije o svim prostim brojevima, |
| \bullet |
\Lambda_{E}(s) - uključuje informacije "u beskonačnosti". Ovu funkciju često nazivamo normalizirana L-funkcija
\Lambda_{E}(s)=\left(\sqrt{N}/2\pi\right)^{s} \cdot \Gamma(s) \cdot L_{E}(s)\, .
|
BSD I.
BSD II daje formulu za c_{r_{\text{}}{an}}, tj. za koeficijent vodečeg člana u Taylorovom razvoju funkcije L_{E}(s) u s=1. Primjetimo da u formuli za c_{r_{\text{}}{an}} sve vrijednosti osim |Ш(E/\mathbb{Q})| dobro razumijemo. Tate-Šafarevičeva grupa je i dalje velika zagonetka. Ne zna se niti je li konačna, iako postoji slutnja da jeste.
| [1] |
Christophe Breuil, Brian Conrad, Richard Taylor, and Fred Diamond. On the modularity of elliptic curves over Q: Wild 3-adic exercises. Journal of the American Mathematical Society, 14(4):843–939, 2001. |
| [2] |
Peter Bruin. Elliptic curves, modularity and the conjecture of Birch and Swinnerton-Dyer, lecture notes. 2016. |
| [3] |
Boris Širola. Distribucija prim brojeva i Riemannova zeta-funkcija. Hrvatski matematički elektronički časopis math.e, (13), 2008. |
| [4] |
Filip Najman. Eliptičke krivulje nad poljima algebarskih brojeva, skripta. 2013. |
| [5] |
Karl Rubin and Alice Silverberg. Ranks of Elliptic Curves. Bulletin (New Series) of the American Mathematical Society, 39(4):455–474, 2002. |
| [6] |
Joseph H. Silverman. The Arithmetic of Elliptic Curves, 2nd Edition, volume 106. Springer-Verlag, New York, 2009. |
| [7] |
Alice Silverberg. Ranks “cheat sheet”. In Women in numbers 2: research directions in number theory, pages 101–110. Contemp. Math., 606, Centre Rech. Math. Proc., Amer. Math. Soc.,Providence, RI, 2013. |
| [8] |
Lawrence C. Washington. Elliptic Curves Number Theory and Cryptography Second Edition. Chapman & Hall/CRT, 2008. |
| [9] |
Wikipedia contributors. Congruent number — Wikipedia the free encyclopedia, 2019. |