Metoda konačnih elemenata; teorija i praktična implementacija
1Uvod
Metoda konačnih elemenata je jedna od najpopularnijih numeričkih metoda za rješavanje parcijalnih diferencijalnih jednadžbi. Cilj ovog rada je na jednostavan način, kroz primjere, prezentirati metodu konačnih elemenata. U prvom dijelu rada je opisana Galerkinova metoda te je kroz jednostavan primjer skrenuta pozornost na opasnosti prilikom numeričke implementacije. U središnjem dijelu rada je opisana metoda konačnih elemenata kao poseban slučaj Galerkinove metode, a kroz primjer je dano numerički prihvatljivije rješenje primjera iz prvog dijela rada, samo što je jedan rub ostavljen slobodnim kako bi se prikazala implementacija raznih rubnih uvjeta. U završnom dijelu rada su dane neke ideje o implementaciji metode konačnih elementa na problemima koji uključuju više derivacije te par komentara vrijednih za praktičnu implementaciju.
2Galerkinova metoda
U ovom odjeljku ćemo postaviti scenu za metodu konačnih elemenata. Započinjemo kratkim opisom Galerkinove metode. Neka je V Hilbertov prostor, a(\cdot , \cdot) : V \times V \to \mathbb{R} bilinearna forma koja je ograničena,
|a(u,v)| \leq M\Vert u\Vert _{V}\Vert v\Vert _{V} \forall u, v \in V
i V-eliptična,
a(v,v) \geq c \Vert v\Vert _{V}^{2} \forall v \in V
te l ograničeni linearni funkcional. Promatramo problem
(1)
u \in V, \hspace{5mm} a(u,v) = l(v) \hspace{5mm} \forall v \in V.
Prema Lax-Milgramovoj lemi, varijacijski problem
(2)
u_{N} \in V_{N}, \hspace{5mm} a(u_{N},v) = l(v) \hspace{5mm} \forall v \in V_{N}.
Uz pretpostavke da je bilinearna forma a ograničena, V - eliptična i l ograničeni linearni funkcional, opet primjenom Lax-Milgramove leme slijedi da
Neka je \lbrace \phi_{i}\rbrace _{i=1}^{N} baza konačnodimenzionalnog prostora V_{N}, tada možemo zapisati
u_{N} = \sum_{j = 1}^{N} \xi_{j}\phi_{j}
za neke, trenutno nepoznate, skalare \xi_{i}, i = 1,2,..,N.
Uzmimo da v \in V_{N} budu baš \phi_{i} te uvrstimo u
(3)
\sum_{j = 1}^{N} a( \phi_{j},\phi_{i})\xi_{j} = l(\phi_{i}) \hspace{5mm} i = 1,...,N.
Očito, prethodnu tvdnju možemo zapisati kao linearni sustav
\mathbf{K\xi = b}
gdje je vektor nepoznanica \mathbf{\xi} = (\xi_{j}) \in \mathbb{R}^{N}, \mathbf{K} = (a(\phi_{j},\phi_{i})) \in \mathbb{R}^{N\times N} matrica sustava te \mathbf{b} = (l(\xi_{i}))\in \mathbb{R}^{N} desna strana.
Općenito je aproksimacija u_{N} različita od rješenja u, stoga je prirodno tražiti približno rješenje u_{N} u potprostoru V_{N} što veće dimenzije. Za niz potprostora V_{N_{i}} takvih da vrijedi V_{N_{1}} \subset V_{N_{2}} \subset ... V_{N}, računamo pripadna rješenja u_{N_{i}}, i = 1,2,.... Ovaj postupak nazivamo Galerkinovom metodom. Prvi korak u dokazu konvergencije Galerkinove metode je važan i elegantan teorijski rezultat.
Teorem 1. (Céina lema) Neka je V Hilbertov prostor, V_{N} \subset V,a( \cdot, \cdot) ograničena, V-eliptična bilinerna forma na V te l ograničeni linearni funkcional. Neka je u \in V rješenje od (1) i u_{N}\in V_{N} Galerkinova aproksimacija (2) . Tada postoji konstanta C takva da
(4)
\Vert u - u_{N}\Vert _{V} \leq C\inf_{v \in V_{N}} \Vert u - v\Vert _{V}.
Proof. Prema pretpostavci a( \cdot, \cdot) je V-eliptična, ograničena bilinearna forma pa za svaki v\in V_{N} imamo,
\begin{align*} c\Vert u - u_{N}\Vert _{V}^{2} &\leq a(u - u_{N}, u - u_{N})\\\& = a(u- u_{N}, u - v)\\\ &\leq M\Vert u - u_{N}\Vert _{V}\Vert u-v\Vert _{V}. \end{align*}
Dijeljenjem s c\Vert u - u_{N}\Vert slijedi tvrdnja,
\Vert u - u_{N}\Vert _{V}^{2} \leq C\Vert u - u_{N}\Vert _{V}\Vert u-v\Vert _{V}
gdje je C = M/c.
\ \blacksquare
U slučaju kada je a(\cdot,\cdot) simetrična bilinearna forma ona definira skalarni produkt na V i njime induciranu normu \Vert v\Vert _{a} = \sqrt{a(v,v)}. Ako sada oduzimemo
a(u-u_{N},v) = 0 \hspace{5mm} \forall v\in V_{N}.
Vidimo da je s obzirom na novi skalarni produkt pogreška u - u_{N} ortogonalna na potprostor V_{N}. Drugim riječima, u_{N} je ortogonalna projekcija egzaktnog rješenja u na potprostor V_{N}.
Korolar 2. Uz pretpostavke prethodnog teorema pretpostavimo još da je dan niz potprostora V_{N_{1}} \subset V_{N_{2}} \subset ... takvih da je \overline{\bigcup_{i}V_{N_{i}}} = V. Tada Galerkinova metoda konvergira,
\Vert u - u_{N_{i}}\Vert \longrightarrow 0 \hspace{4mm} \text{ kad }i \longrightarrow \infty.
Proof. Zbog pretpostavke gustoće postoji niz v_{i} \in V_{N_{i}}, i \geq 1, takav da
\Vert u - v_{i}\Vert _{V}\longrightarrow 0 \hspace{4mm} \text{ kad } i \longrightarrow \infty.
Primjenom Céine leme slijedi dokaz tvrdnje,
\Vert u - u_{N_{i}}\Vert _{V} \leq C\Vert u-v_{i}\Vert _{V}.
\ \blacksquare
Promotrimo primjenu Galerkinove metode na jednostavnom primjeru.
Primjer 3. Zadan je rubni problem
Množenjem s test funkcijom v \in V = H_{0}^{1}(\langle0,1\rangle), integriranjem po cijeloj domeni te primjenom parcijalne integracije slijedi slaba formulacija
Moramo odabrati konačnodimenzionalni potprostor od V u kojem želimo tražiti aproksimaciju rješenja. S obzirom na to da je rješenje u rubovima nula jedan jednostavan potprostor je
Kao posljednji argument koji ide u prilog numeričkoj nestabilnosti implementacije Galerkinove metode pogledajmo sljedeće slike.
(5)
\begin{cases}-u'' + u = f \text{ na } \langle0,1\rangle\\ u(0) = u(1) = 0. \end{cases}
u\in V, \hspace{5mm} \int_{0}^{1}(u'v' + uv)dx = \int_{0}^{1}fvdx, \hspace{5mm} \forall v\in V.
Ako definiramo a(u,v) = \int_{0}^{1}(u'v' + uv)dx te l(v) = \int_{0}^{1}fvdx iz Lax-Milgramove leme slijedi jedinstvenost rješenja ovako zapisane zadaće.Moramo odabrati konačnodimenzionalni potprostor od V u kojem želimo tražiti aproksimaciju rješenja. S obzirom na to da je rješenje u rubovima nula jedan jednostavan potprostor je
V_{N} = span\lbrace x^{i}(1-x), i = 1,2,...,N\rbrace .
Onda je
u_{N} = \sum_{j = 1}^{N} \xi_{j}x^{j}(1-x).
Nepoznate koeficijente \lbrace \xi_{j}\rbrace _{j = 1}^{N} odredit ćemo iz Galerkinovih jednadžbi
\int_{0}^{1}(u_{N}'v' + u_{N}v)dx = \int_{0}^{1} fv dx\hspace{5mm} \forall v\in V_{N},
uzimanjem funkcija v = x^{i}(1-x),i= 1,2,...,N za test funkcije. Dolazimo do sustava linearnih jednadžbi
\mathbf{K\xi = b},
gdje je {\mathbf{\xi} }= (\xi_{1},...,\xi_{N})^{\tau} vektor nepoznanica, \mathbf{b} \in \mathbb{R}^{N} vektor desne strane čija je i-ta komponenta oblika \int_{0}^{1} f(x)x^{i}(1-x)dx te \mathbf{K} matrica sustava čiji (i,j) element ima oblik
\begin{align*} \int_{0}^{1} \left[\left(x^{j}(1-x)\right)'\left(x^{i}(1-x)\right)' + x^{j}(1-x)x^{i}(1-x)\right]dx &= \frac{ij}{i+j-1} - \frac{i(j+1) j(i+1)}{i+j} + \frac{(i+1)(j+1)}{i+j+1}\\\ &+ \frac{1}{i+j+1} - \frac{2}{i+j+2} + \frac{1}{i+j+3}. \end{align*}
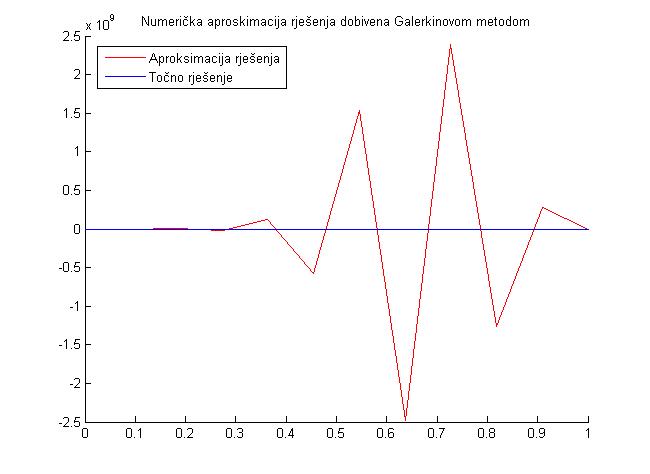
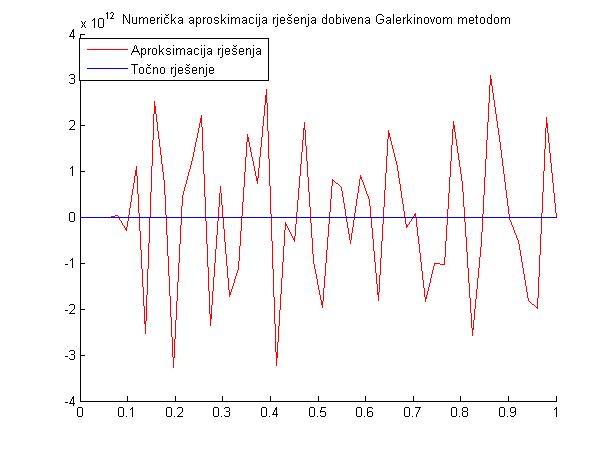
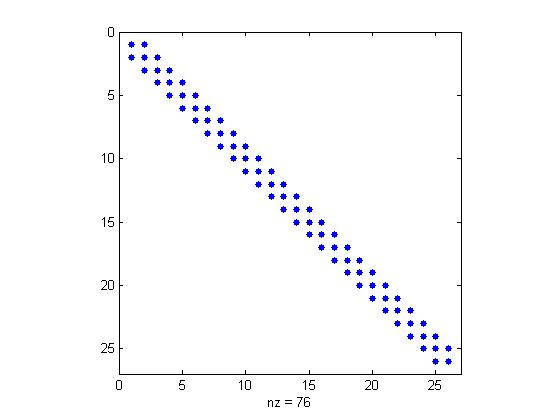
Valja odmah primijetiti da je matrica koeficijenata \mathbf{K} popunjena elementima različitim od nule. No to nije sve, matrica je i loše uvjetovana što upućuje na ozbiljne opasnosti prilikom numeričkog rješavanja dobivenog sustava. U sljedećoj tablici je prikazana uvjetovanost matrice sustava za neke dimenzije potprostora.
\begin{array}{c|c}N& Cond(K)\\\ 3& 1.90 \cdot 10^{2} \\\ 5& 7.88 \cdot 10^{4}\\\ 7& 4.43 \cdot 10^{7}\\\ 10& 7.87 \cdot 10^{11}\\\ \end{array}
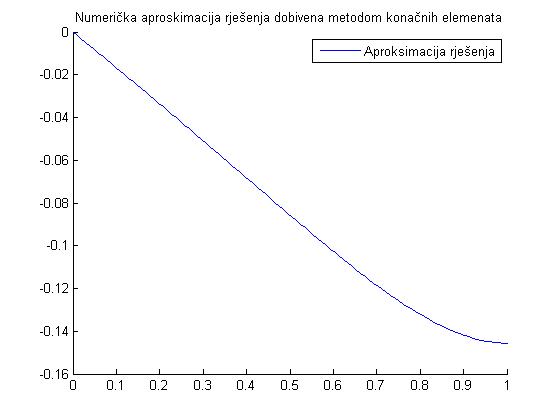
Kao posljednji argument koji ide u prilog numeričkoj nestabilnosti implementacije Galerkinove metode pogledajmo sljedeće slike.
Slika 1: Rezultati numeričke implementacije Galerkinove metode za f(x) = -x^{3} čije egzaktno rješenje je dano s u(x)=\frac{-7e^{x}}{e^{-1} - e}+\frac{7e^{-x}}{e^{-1} - e} - x^{3} - 6x.
a) Za n = 10, apsolutna pogreška je 7.87e\cdot 10^{11}, a uvjetovanost matice sustava je 4.02\cdot 10^{9}
b) Za n = 50, apsolutna pogreška je 1.11\cdot 10^{13} te uvjetovanost matice sustava je 5.28\cdot 10^{15}
c) Egzaktno rješenje
d) Popunjenost matrice krutosti za n = 25. Plava točkica označava ne-nul element u matrici na odgovarajućem mjestu.
a) Za n = 10, apsolutna pogreška je 7.87e\cdot 10^{11}, a uvjetovanost matice sustava je 4.02\cdot 10^{9}
b) Za n = 50, apsolutna pogreška je 1.11\cdot 10^{13} te uvjetovanost matice sustava je 5.28\cdot 10^{15}
c) Egzaktno rješenje
d) Popunjenost matrice krutosti za n = 25. Plava točkica označava ne-nul element u matrici na odgovarajućem mjestu.
Iako je s teorijske strane ovaj pristup jednostavan i elegantan, neke detalje ćemo ipak morati prilagoditi kako bismo osigurali spomenuta dobra svojstva i praktičnoj izvedbi.
3Metoda konačnih elemenata
U prethodnom primjeru prilikom numeričke izvedbe Galerkinove metode vidjeli smo da se rješavanje linearnog rubnog problema svodi na rješavanje sustava linearnih jednadžbi. No, matrica sustava je bila gusto popunjena i loše uvjetovana. Htjeli bismo prilagoditi Galerkinovu metodu tako da u konačnici dobijemo sustav koji je dobro uvjetovan i još po mogućnosti rijetko popunjen. Ipak, za računanje svakog elementa matrice potrebno je riješiti ponekad netrivijalan integral - što je vremenski skupo ukoliko je matrica gusto popunjena. Kada radimo sa sustavima čije su matrice rijetko popunjene otvara se još jedan bonus, mogućnost uporabe iterativnih metoda. Jedan način na koji možemo riješiti prethodna dva problema jest pažljivim odabirom baze konačnodimenzionalnog prostora V_{N}. Zathjevat ćemo da je broj baznih funkcija čiji se nosači sijeku s nosačem proizvoljne bazne funkcije što manji mogući. Odlučit ćemo se za prostor V_{N} koji se sastoji od funkcija koje su po dijelovima polinomi povezani s diskretizacijom domene \Omega. Jednostavno govoreći, Galerkinova metoda uz prethodne pretpostavke na bazne funkcije postaje metoda konačnih elemenata.
Konvergencija metode konačnih elemenata može se postići povećanjem stupnja polinoma u baznim funkcijama, profinjavanjem diskretizacije domene ili čineći obje istovremeno. Ilustrirajmo sada na primjeru navedene ideje.
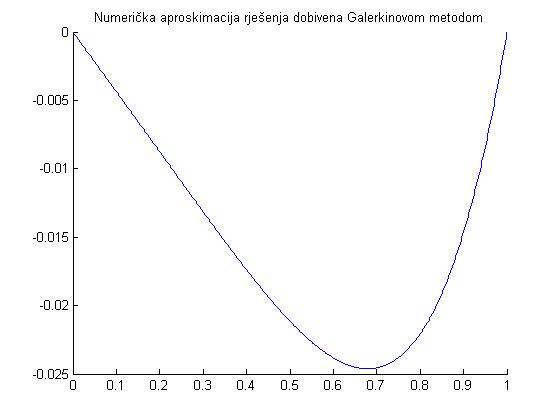
Primjer 4. Promatramo
gdje je f\in L(\langle0,1\rangle) te b\in \mathbb{R}. Kao prije množenje s test funkcijom v \in V = \lbrace v \in H^{1}(\langle0,1\rangle) : v(0) = 0\rbrace, integriranjem po cijeloj domeni te primjenom parcijalne integracije daje slabu formulaciju
Za N \in \mathbb{N} načinimo diskretizaciju domene I = [0, 1] tako da je 0 = x_{0} \lt x_{1} \lt ... \lt x_{N} = 1. Točke x_{i} nazivamo čvorovi, a podintervale I_{i} = [x_{i-1}, x_{i}] elementi. Označimo s h_{i} = x_{i} - x_{i-1} te s h = \max_{i = 1,...,N}h_{i}. Rješenje ćemo tražiti u prostoru
Neka je zadan prostor konačnih elemenata
koji prema Lax-Milgramovoj lemi ima jedinstveno rješenje. Kao i u prethodnom primjeru, ako zapišemo aproksimaciju rješenja kao linearnu kombinaciju elemenata baze,
(7) može zapisati kao
(7) prikazati kao sustav linearnih jednadžbi \mathbf{Ku = b}.
Na kraju primjera pogledajmo rezultate programske implementacije metode konačnih elemenata.
(6)
\begin{cases}-u'' + u = f \text{ na } \langle0,1\rangle\\ u(0) = 0, u'(1) = b \end{cases}
u\in V, \hspace{5mm} \int_{0}^{1}(u'v' + uv)dx = \int_{0}^{1}fvdx + bv(1), \hspace{5mm} \forall v\in V.
Opet, primjenom Lax-Milgramove leme slijedi da slaba formulacija ima jedinstveno rješenje.Za N \in \mathbb{N} načinimo diskretizaciju domene I = [0, 1] tako da je 0 = x_{0} \lt x_{1} \lt ... \lt x_{N} = 1. Točke x_{i} nazivamo čvorovi, a podintervale I_{i} = [x_{i-1}, x_{i}] elementi. Označimo s h_{i} = x_{i} - x_{i-1} te s h = \max_{i = 1,...,N}h_{i}. Rješenje ćemo tražiti u prostoru
V_{h} = \lbrace v_{h} \in V : v_{h}|_{I_{i}}\in \mathcal{P}_{1}(I_{i}), i = 1,...,N\rbrace .
Zato što su po dijelovima glatke funkcije u H^{1}(I) ako i samo ako su u C(\overline{I}), ekvivaletno možemo definirati
V_{h} = \lbrace v_{h} \in C(\overline{I}) : v_{h}|_{I_{i}}\in \mathcal{P}_{1}(I_{i}), i = 1,...,N, v(0) = 0\rbrace .
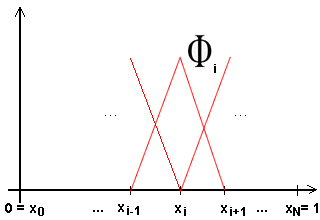
Za bazne funkcije uvodimo tzv. hat funkcije
\begin{align*} \phi_{i}(x) = \begin{cases} (x - x_{i-1})/h_{i}, \hspace{5mm} &x_{i-1}\leq x \leq x_{i},\\ (x_{i+1}-x)/h_{i+1}, \hspace{5mm} &x_{i}\leq x \leq x_{i+1}, \\ 0, \hspace{5mm} &\text{inače}, \end{cases} \end{align*}
i posebno za desni rub kada je i = N,
\begin{align*} \phi_{i}(x) = \begin{cases} (x-x_{N-1})/h_{N}, \hspace{5mm} &x_{N-1}\leq x \leq x_{N}, \\ 0, \hspace{5mm} &\text{inače}, \end{cases} \end{align*}
Prethodne funkcije su neprekidne, po dijelovima glatke i očito linearno nezavisne. Lako se vidi da je prva slaba derivacija tako definiranih funkcija \phi_{i} po dijelovima konstantna funkcija.
Neka je zadan prostor konačnih elemenata
V_{h} = span\lbrace \phi_{i} : i = 1,...,N\rbrace
uz problem
(7)
u_{h}\in V_{h} \hspace{5mm} \int_{0}^{1}(u_{h}'v_{h}' + u_{h}v_{h})dx = \int_{0}^{1}fv_{h}dx + bv_{h}(1) \hspace{5mm} \forall v\in V_{h},
u_{h} = \sum_{j = 1}^{N}u_{j}\phi_{j}
vidimo da se
\sum_{j=1}^{N}u_{j}\int_{0}^{1}(\phi_{i}'\phi_{j}' + \phi_{i}\phi_{j})dx = \int_{0}^{1}f\phi_{i}dx+b\phi_{i}(1), \hspace{5mm} i = 1,..., N.
Lako je provjeriti istinitost sljedećih formula, a njihovo uvažavanje će biti ključno za sastavljanje matrice sustava.
\begin{align*} \int_{0}^{1}\phi_{i}'\phi_{i-1}'dx &= -\frac{1}{h}, \hspace{5mm} i = 2,...,N,\\\ \int_{0}^{1}(\phi_{i}')^{2}dx &= \frac{2}{h}, \hspace{5mm} i =2,...,N-1,\\\ \int_{0}^{1}\phi_{i}\phi_{i-1}dx &= -\frac{h}{6}, \hspace{5mm} i = 2,...,N,\\\ \int_{0}^{1}(\phi_{i})^{2}dx &= \frac{2h}{3}, \hspace{5mm} i = 1,...,N-1,\\\ \int_{0}^{1}(\phi_{N}')^{2}dx &= -\frac{1}{h},\\\ \int_{0}^{1}(\phi_{N})^{2}dx &= -\frac{h}{3}. \end{align*}
Sada možemo problem
\begin{align*} \mathbf{K} = \begin{bmatrix} \frac{2h}{3} + \frac{2}{h}& \frac{h}{6}- \frac{1}{h}&& \\\ \frac{h}{6}- \frac{1}{h}& \frac{2h}{3} + \frac{2}{h}& \frac{h}{6}- \frac{1}{h}& \\\ \ddots& \ddots& \ddots&& \\\& \frac{h}{6}- \frac{1}{h}& \frac{2h}{3} + \frac{2}{h}& \frac{h}{6}- \frac{1}{h} \\\&& \frac{h}{6}- \frac{1}{h}& \frac{h}{3} + \frac{}{h} \end{bmatrix} \end{align*}
je matrica sustava,
\mathbf{b} = \left(\int_{0}^{1}f\phi_{1}dx, \int_{0}^{1}f\phi_{2}dx,...,\int_{0}^{1}f\phi_{N-1}dx,\int_{0}^{1}f\phi_{N}dx + b\right)^{\tau}
vektor desne strane te
\mathbf{u} = (u_{1},...,u_{N})^{\tau}
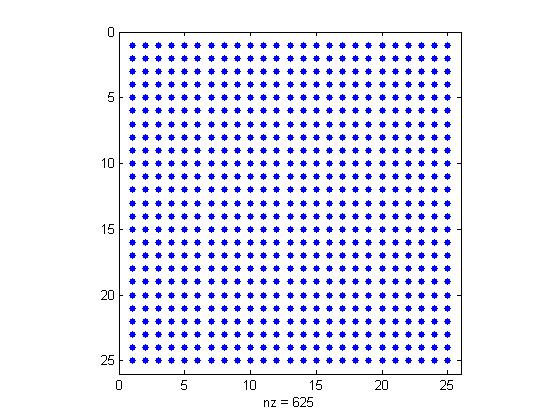
vektor nepoznanica. Zahtijevali smo da bazne funkcije imaju što manji mogući nosač, posljedica je rijetko popunjena matrica sustava \mathbf{K} matrica. Dobra uvjetovanost matrice \mathbf{K} pokazana u sljedećoj tablici.
\begin{array}{ l | r } N& Cond(K)\\\ 3& 22.3962\\\ 5& 22.3962\\\ 7& 22.3962\\\ 10& 43.1613\\\ \end{array}
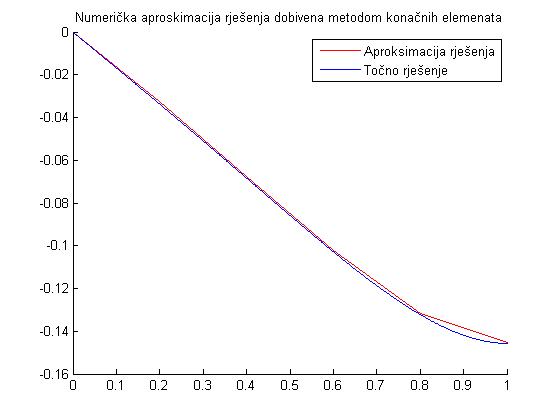
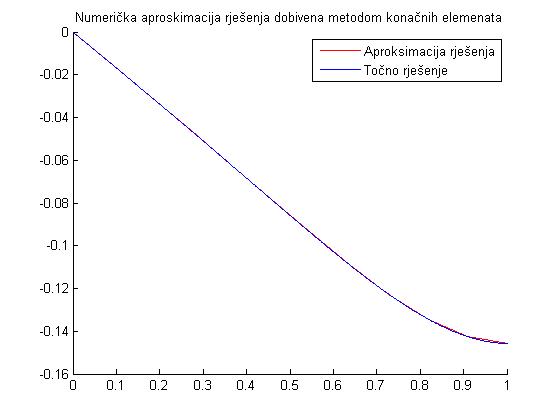
Na kraju primjera pogledajmo rezultate programske implementacije metode konačnih elemenata.
Slika 3: Rezultati numeričke implementacije metode konačnih elemenata za f(x) = -x^{3} uz rubne uvjete u(0) = u'(1) = 0 čije egzaktno rješenje je dano s u(x)=\frac{9e^{x}}{e^{-1} + e}-\frac{9e^{-x}}{e^{-1} + e} - x^{3} - 6x.
a) Egzaktno rješenje
b) Za n = 4, apsolutna pogreška je 0.0015, a uvjetovanost matice sustava je 32.64
c) Za n = 10, apsolutna pogreška je 9.62 \cdot 10^{-5} te uvjetovanost matice sustava je 150.25.
d) Popunjenost matrice \mathbf{K} za n = 25. Plava točkica označava ne-nul element na odgovarajućem mjestu u matrici.
a) Egzaktno rješenje
b) Za n = 4, apsolutna pogreška je 0.0015, a uvjetovanost matice sustava je 32.64
c) Za n = 10, apsolutna pogreška je 9.62 \cdot 10^{-5} te uvjetovanost matice sustava je 150.25.
d) Popunjenost matrice \mathbf{K} za n = 25. Plava točkica označava ne-nul element na odgovarajućem mjestu u matrici.
4Još jedan primjer
U nastavku promotrimo jednadžbu koja opisuje otklon žice klavira pod utjecajem sile f. Žica klavira ima dva dijela; žičanu jezgru te žicu namotanu oko nje. Uzevši to u obzir, jasno je da se takav objekt ne ponaša isključivo kao tanka žica. Žica klavira vibrira dijelom zbog napetosti, a dijelom zbog same čvrstoće žice. Iz tog razloga modelu dodajemo član koji opisuje ponašanje tankog štapa.
(8)
\begin{cases}u^{(4)} - u^{''} = f \text{ na } \langle0,1\rangle\\ u(0) = u'(0) = u(1) = u'(1) = 0. \end{cases}
Slaba formulacija problema je
u\in V, \hspace{5mm} \int_{0}^{1}(u''v'' + u'v')dx = \int_{0}^{1}fvdx \hspace{5mm} \forall v\in V,
gdje je V = H_{0}^{2}(\langle0,1\rangle). Ako želimo odabrati V_{h}, takav da je V_{h} \subset V, onda svaka funkcija u V_{h} mora bit barem klase \mathcal{C}^{1}. Pretpostavimo da se V_{h} sastoji od po dijelovima polinoma stupnja manjeg ili jednakog p. Uvjet da su funkcije u V_{h} klase \mathcal{C}^{1} nameće 2(N-1) uvjeta, a rubni uvjeti još 4 uvjeta. Sve skupa imamo
dim(V_{h}) = (p+1)N - 2(N-1) - 4 = (p-1)N - 2
stupnja slobode da odaberemo bazne funkcije sa što manjim nosačem. Jasno je da je najmanji dozvoljeni p = 2. Međutim odlučit ćemo se za p = 3 da bismo povećali broj stupnjeva slobode za odabir baznih funkcija. Za p =3 prostor konačnih elemenata je
V_{h} = \lbrace v_{h}\in \mathcal{C}^{1}(\overline{I}) : v_{I_{i}}\in \mathcal{P}_{3}(I_{i}), I =1,...,N, v_{h}(x) = v_{h}'(x) = 0 \text{ za } x = 0,1\rbrace .
Možemo konstruirati bazne funkcije s malim nosačima koristeći uvjete interpolacije
\begin{align*} \phi_{i}(x_{j}) = \delta_{ij}, \hspace{4mm} \phi_{i}'(x_{j}) = 0,\\ \psi_{i}(x_{j}) = 0, \hspace{4mm} \psi_{i}'(x_{j}) = \delta_{ij}. \end{align*}
Kako bismo izbjegli tehničke komplikacije, poželjno je raditi na referentnom elementu. Ideja je sav posao obaviti na jednom elementu, tzv. referentnom elementu, a onda postignuto preslikati na ostale elemente. Neka je I_{0} = \langle 0, 1\rangle, preslikavanje
F_{i} : I_{0} \to I_{i}, \hspace{5mm} F_{i}(\xi) = x_{i-1}+h_{i}\xi
je bijekcija. Na referentnom elementu I_{0} konstruiramo polinome trećeg stupnja koji zadovoljavaju interpolacijske uvjete
\begin{align*} \Phi_{0}(0) = 1, \hspace{4mm} \Phi_{0}(1) = 0,\hspace{4mm} \Phi_{0}'(0) = 0,\hspace{4mm} \Phi_{0}'(1) = 0,\\\ \Phi_{1}(0) = 0, \hspace{4mm} \Phi_{1}(1) = 1,\hspace{4mm} \Phi_{1}'(0) = 0,\hspace{4mm} \Phi_{1}'(1) = 0,\\\ \Psi_{0}(0) = 0, \hspace{4mm} \Psi_{0}(1) = 0,\hspace{4mm} \Psi_{0}'(0) = 1,\hspace{4mm} \Psi_{0}'(1) = 0,\\\ \Psi_{1}(0) = 0, \hspace{4mm} \Psi_{1}(1) = 0,\hspace{4mm} \Psi_{1}'(0) = 0,\hspace{4mm} \Psi_{1}'(1) = 1. \end{align*}
Jednostavnim računom određujemo da su tražene funkcije
\begin{align*} &\Phi_{0} (\xi) = (1+2\xi)(1-\xi)^{2},\\ &\Phi_{1} (\xi) = (3-2\xi)\xi^{2}, \\ &\Psi_{0}(\xi) = \xi(1-\xi)^{2},\\ &\Psi_{1}(\xi) = -(1-\xi)\xi^{2}. \end{align*}
Sad možemo odrediti bazne funkcije
\begin{align*} \phi_{i} = \begin{cases} \Phi_{1}(F_{i}^{-1}(x)), \hspace{5mm} &x\in I_{i},\\ \Phi_{0}(F_{i+1}^{-1}(x)), &x\in I_{i+1},\\ 0, &\text{inače}, \end{cases} \end{align*}
i
\begin{align*} \psi_{i} = \begin{cases} h_{i}\Psi_{1}(F_{i}^{-1}(x)), \hspace{5mm} &x\in I_{i},\\ h_{i+1}\Psi_{0}(F_{i+1}^{-1}(x)), &x\in I_{i+1},\\ 0, &\text{inače}, \end{cases} \end{align*}
Kao i u prethodnim primjerima, želimo formulirati sustav linearnih jednadžbi. Koeficijente matrice sustava računat ćemo preko referentnog elementa, npr.
\begin{align*} k_{i-1,i} = \int_{0}^{1}(\phi_{i-1})''(\phi_{i})''+ (\phi_{i-1})'(\phi_{i})'dx = \int_{I_{i}}(\phi_{i-1})''(\phi_{i})'' + (\phi_{i-1})'(\phi_{i})'dx \end{align*}
koristeći definiciju baznih funkcija i funkcije F_{i} možemo izračunati
\begin{align*} k_{i-1,i} &= \frac{1}{h_{i}^{3}}\int_{I_{0}}6(2\xi-1)6(1-2\xi)d\xi + \frac{1}{h_{i}}\int_{I_{0}}6\xi(\xi-1)6\xi(1-\xi)d\xi\\ &= -\frac{12}{h_{i}^{3}} - \frac{6}{5h_{i}}. \end{align*}
Ostale elemente matrice možemo izračunati analogno, a tako dobivena matrica će biti petdijagonalna. Komentirajmo za kraj da je za višedimenzionalne probleme tehnika referentnog elementa neophodna, kako za teorijsku analizu greške tako i za praktičnu implementaciju. Valja primijetiti da smo u prethodnom jednodimenzionalnom primjeru zahtijevali da funkcije iz V_{h} budu polinomi trećeg stupnja kako bismo postigli da funkcije iz V_{h} \subset V budu klase \mathcal{C}^{1}. U višim dimenzijama je potreban još veći stupanj polinoma kako bismo to postigli. Jedan način kako je moguće riješiti taj problem jest korištenjem nekonformnih elemenata ([5]).
Za sam kraj, ostavljamo čitatelju jedan programerski podhvat.
Zadatak. Napravite programsku izvedbu metode konačnih elemenata za sljedeći problem
(9)
\begin{cases}u^{(4)} - u^{''} = -x^{3} \text{ na } \langle0,1\rangle\\ u(0) = u'(0) = u(1) = u'(1) = 0. \end{cases}
Egzaktno rješenje ovog problema je
\begin{align*}u(x) =& \frac{1}{20(e-3)(e-1)}\cdot e^{-x}(e^{x+2}(x^{5}+20x^{3}-44x+44) - 2e^{x+1}(2x^{5}+40x^{3}-65x+44)\\\ &+e^{x}(3x^{5}+60x^{3}-86x-86)+86e^{2x}-21e^{2x+1}-44e^{2}+109e). \end{align*}
Zahvaljujem se prof.dr.sc. Josipu Tambači na detaljnom čitanju ovog članka i korisnim savjetima.
5Literatura
[1] Atkinson, Han. Theoretical Numerical Analysis: a functional framework. Vol 19. Springer, 2009.
[2] Dhatt, Gouri i Touzot, Gilbert. Finite Element Method. John Willey and Sons, 2012.
[3] Brenner, Susanne i Carstensen, Carsten. Encyclopedia of Computational Mechanics. Chapter 4, Finite Element Methods. John Wiley and Sons, 2004.
[4] Jurak, Mladen. Praktikum primijenjene matematike II. Skripta, PMF Matematički odsjek, 2008.
[5] Ciarlet, Philippe G. The finite element method for elliptic problems. Elsevier, 1978.
