Ključne riječi: internetski pretraživač, PageRank algoritam, metoda potencija, GNU Octave

Moderni život gotovo je nezamisliv bez interneta, koji omogućava nikada brži i jednostavniji pristup informacijama. Veliku ulogu u tome imaju internetski pretraživači (tražilice). Internetski pretraživač ili tražilica softverski je sustav koji je osmišljen za provođenje internetskog pretraživanja, tj. sustavnog pretraživanja World Wide Weba s ciljem pronalaska određenih podataka navedenih u tekstualnom upitu [3]. Na temelju unesenog pojma pretraživač daje popis relevantnih internetskih stranica, pri čemu, što je stranica relevantnija za uneseni pojam, to se nalazi bliže vrhu rezultata pretraživanja. Prvi pretraživači devedesetih godina prošlog stoljeća su rangirali stranice na temelju indeksiranja – prolazili su kroz svaku stranicu i brojali koliko puta se traženi pojam pojavljuje na određenoj stranici. Takav način u moderno vrijeme je neefikasan, jer je s vremenom značajno porastao broj internetskih stranica te je stoga postalo vremenski neefikasno prolaziti kroz svaku internetsku stranicu. Također, takav pristup nije dobar prikaz relevantnih stranica, jer neka stranica može sadržavati uneseni pojam puno puta, bez da sadrži korisne informacije o njemu. Moderni pretraživači, npr. Googleova tražilica, koriste drukčije pristupe pri rangiranju internetskih stranica. Rangiranje internetskih stranica od strane Googlea obuhvaća brojne kriterije (često se navodi 200 ili više kriterija), kao što je brzina učitavanja stranice, povezanost, posjećenost, sigurnost, lokacija itd. [5]. PageRank algoritam spominje se u nekoliko kriterija, a uzima u obzir posjećenost, važnost i popularnost neke internetske stranice. Google je najpopularniji internetski pretraživač na svijetu. Svakodnevno se izvršava više od 3,5 milijardi pretraga odnosno 40 tisuća svake sekunde [4]. Prema statistici NetMarket Sharea, za razdoblje od svibnja 2019. do travnja 2021. godine, Google zauzima daleko najveći udio na tržištu internetskih pretraživača sa 82,80% korisnika. Kineski Baidu je sljedeći po popularnosti s 7,70%, a odmah iza njega nalazi se Bing (6,28%) [9]. Na Slici 1 prikazana je zastupljenost internetskih pretraživača za navedeno razdoblje.

Slika 1: Zastupljenost internetskih pretraživača za razdoblje 05.2019. – 04.2021 [9]

.

Metoda potencija najjednostavnija je metoda za određivanje najveće (po apsolutnoj vrijednosti) svojstvene vrijednosti matrice i pripadnog svojstvenog vektora. Algoritam metode potencija je vrlo jednostavan i iterativan, ali ponekad sporo konvergira. U slučaju rijetko popunjene matrice A (matrica u kojoj većina elemenata ima vrijednost nula), metoda potencija je vrlo brza. Neka je matrica A matrica dijagonalizabilna i neka ima jedinstvenu po apsolutnoj vrijednosti najveću svojstvenu vrijednost. Tada su svojstvene vrijednosti matrice A\lambda_{1},\lambda_{2},…,\lambda_{n} i neka su poredane tako da vrijedi

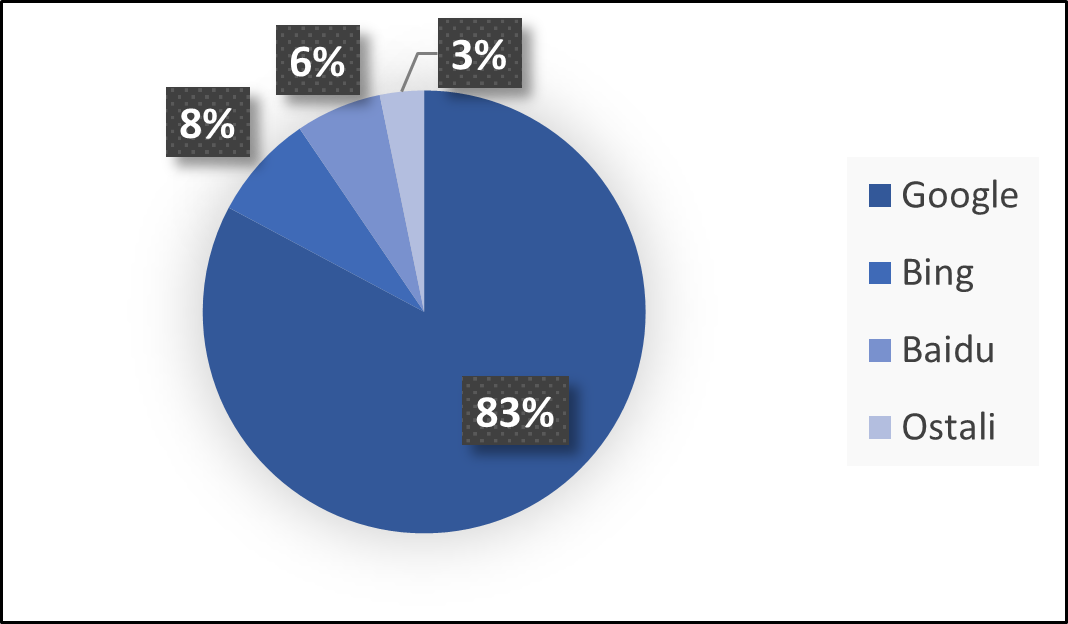
Neka je x^{(0)} početni vektor. Tada se metoda potencija svodi na množenje matrice A vektorom x^{(k)} u svakoj iteraciji, tj.

Budući da elementi umnoška Ax^{(k)} mogu postati jako veliki ili jako mali brojevi, potrebno je normirati vektore x^{(k)}, k = 0, 1, .... Algoritam metode potencija možemo zapisati kao u Algoritmu 1. 

Kriterij konvergencije može biti zadani broj iteracija ili tolerancija na razliku između rješenja dvije susjedne iteracije.Nešto više o metodi i njenoj konvergenciji može se pronaći u [2].

PageRank je algoritam koji koristi tvrtka Google u svom internetskom pretraživaču prilikom rangiranja internetskih stranica. PageRank algoritam dobio je ime po Larryu Pageu, jednom od osnivača Googlea. U ranim devedesetima prošlog stoljeća, kada su internetski pretraživači koristili samo tekstualne sustave rangiranja postojao je niz problema. Potraga za pojmom kao što je "Matematika" bila je problematična. Najviše rangirana stranica koju bi prikazivala jedna od ranijih internetskih pretraživača bila bi napisana na kineskom jeziku s ponavljanjima riječi "Matematika" i ne bi sadržavala nikakav drugi podatak. Također, kada bi se tražile informacije o riječi "matrica" očekivalo se da bi stranica "www.matrica.hr" bila najrelevantnije mjesto za takav upit. Međutim, mogu postojati milijuni stranica koje koriste riječ "matrica" u svojoj domeni, a stranica www.matrica.hr možda nije ona koja se najčešće koristi. Neka internetska stranicu sadrži riječ "matrica" milijun puta i ništa drugo. Zar bi tada imalo smisla da ta internet stranica bude prikazana prva u pretraživaču bez obzira što sadržaj stranice nije relevantan? Međutim, ako je broj ponavljanja tražene riječi na nekoj stranici osnovni kriterij rangiranja, onda se upravo to događalo. Navedeni problemi su motivirali nove i bolje pristupe rangiranju stranica. Jedno od tih novijih rješenja je i PageRank algoritam [6].

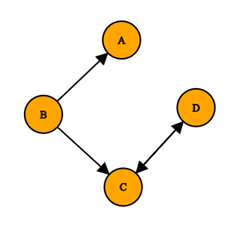
PageRank algoritam za računanje važnosti i kvalitete internet stranica, ne uzima u obzir samo broj poveznica do neke stranice, nego i kvalitetu tih poveznica kako bi odredio grubu procjenu važnosti internetske stranice. Temeljna pretpostavka je da će važnije internetske stranice dobiti više poveznica s drugih internetskih stranica. To se najbolje može dočarati ako se internet interpretira kao veliki usmjereni graf, gdje vrhovi predstavljaju internetske stranice, a poveznice među stranicama su bridovi grafa. Ideja i funkcionalnost PageRank algoritma demonstrirat će se kroz nekoliko primjera. Pritom će se koristiti metoda potencija kako bi se izračunao prvi svojstveni vektor, koji predstavlja rang internetskih stranica. Radi jednostavnosti poveznice (bridovi) među stranicama (vrhovima grafa) neće imati težine. U nastavku će poveznice i bridovi te stranice i vrhovi imati jednako značenje.

Postoje internetske stranice koje nude izračunavanje ranga neke domene PageRank algoritmom besplatno, npr. [7] koja koristi skalu 0-10, pri čemu je 10 najveći rang. Tako je moguće provjeriti da stranica Veleučilišta u Virovitici, kao relativno mladog učilišta, ima PageRank 5, dok npr. velika i tradicijom bogata sveučilišta Fakultet elektrotehnike i računarstva te Prirodoslovno-matematički fakultet u Zagrebu imaju PageRank 8, a Googleov internetski pretraživač i Facebook imaju PageRank 9.

Projekt Opte [10] je nastojanje izrade vizualizacijske mape cijelog interneta. Navedena stranica nudi brojne vizualizacije rasta Interneta kroz povijest i načine prikazivanja mape Interneta. Npr. možemo vidjeti zastupljenost po kontinentima i važnost stranica. Jedna ilustracija vizualizacije dana je na Slici 3.

Slika 3: Jedna od ilustracija mape interneta - Opte projekt.

Primjer 1. Prvi primjer sastoji se od četiri internetske stranice koje su povezane kao na Slici 4. Nije bitan samo broj poveznica na neku internetsku stranicu, već i kvaliteta internetskih stranica od kojih dolaze poveznice. Tako npr. stranica A i stranica D mogu imati različitu važnost bez obzira što obje stranice imaju samo jednu ulaznu poveznicu. Prvi korak je prikazivanje grafa u obliku modificirane matrice susjedstva. Zamislimo da svaka stranica ima jedan „bod“ koji raspodjeljuje s drugim stranicama s kojima je povezana. Nadalje, svakoj stranici pripada jedan redak u matrici, stranici A prvi redak, stranici B drugi, stranici C treći i stranici D četvrti redak matrice. Ukoliko neka stranica pokazuje na dvije stranice, taj bod se dijeli između te dvije stranice, odnosno vrha. Npr., stranica B dodjeljuje pola boda stranici A, a drugu polovicu stranici C. Isti princip koristimo za svaki vrh u usmjerenom grafu koji prikazuje danu mrežu. Važno je naglasiti da je usmjerenost grafa bitna odrednica, jer npr. stranica B može pokazivati na stranicu A, ali obrnuto ne mora vrijediti. Element matrice susjedstva na poziciji (i, j) bit će različit od nula, ako postoji poveznica sa i-te stranice na j-tu stranicu u mreži. Matrica susjedstva u ovom primjeru glasi

A = \left[ \begin{matrix} 0 & 0 & 0 & 0\\ 1& 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0\\ \end{matrix} \right].

Tada u modificiranoj matrici susjedstva Q u i-tom retku, uz uvjet da nije nul redak, stoji

Q_{ij} = \frac{A_{ij}}{\sum_{j = 1}^{n} A_{ij}},

a nul redci se ne mijenjaju. Isti princip vrijedi za svaku stranicu, čime se dobiva matrica:

Q = \left[ \begin{matrix} 0 & 0 & 0 & 0\\ \frac{1}{2} & 0 & \frac{1}{2} & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0\\ \end{matrix} \right].

Rang stranica može se dobiti korištenjem metode potencija za matricu koje reprezentira usmjereni graf mreže. Za početnu iteraciju, svaki element vektora r je jednake vrijednosti, jer se na početku uzima da svaka stranica ima jednaki rang, dakle

r = \left( \frac{1}{4}, \frac{1}{4}, \frac{1}{4}, \frac{1}{4} \right).

Ovakav pristup ima nekoliko problema, a za njihovo razumijevanje i rješavanje uvodimo pojam slučajnog šetača.

Slika 4: Graf mreže koja sadrži četiri internet stranice (vrhovi A, B, C, D). a usmjereni bridovi pokazuju povezanost tih stranica.

 

Za dublje razumijevanje PageRank algoritma potrebno je znanje osnova vjerojatnosti. Model slučajnog šetača pretpostavlja da je sljedeća stranica odabrana nasumično. Dakle, rješenje PageRank metode se može promatrati kao asimptotsku vjerojatnost da je slučajni šetač na određenoj stranici. Što je rang stranice veći, veća je vjerojatnost da će slučajni šetač doći do te stranice. Opisana metoda u prošlom odjeljku ima dva problema: „zaglavljen“ u stranici i „zaglavljen“ u podgrafu. Rješenja za te probleme su opisana u nastavku.

U grafu mogu postojati vrhovi koji nemaju izlaznih bridova (tzv. ponori), tj. postoje stranice koje ne pokazuju niti na jednu drugu stranicu. Tada slučajni šetač ne bi mogao otići niti u jednu drugu internet stranicu. U Primjeru 1 slučajni šetač će „zaglaviti“ u slučaju da dođe u vrh A, jer taj vrh ne pokazuje niti na jedan drugi vrh, dok vrhovi B, C i D pokazuju na barem jedan drugi vrh. Taj problem se može riješiti tako da se provjeri zbroj svakog retka modificirane matrice susjedstva Q i ukoliko je on jednak nuli, svaku nulu je potrebno zamijeniti s vrijednosti 1/n, pri čemu je n ukupni broj vrhova. Stvorene su „nevidljive“ poveznice koje zapravo ne postoje između vrhova, ali sprječavaju da šetač zaglavi u nekom vrhu, jer sada postoji vjerojatnost da iz tog vrha skoči u bilo koji vrh. Dodavanjem novih poveznica mijenjaju se vrijednosti matrice Q, čime se generira matrica \hat{Q}. Matrica \hat{Q} je tada redak stohastička - zbroj elemenata u svakom retku iznosi jedan. Dobiva se tako da matrici Q dodamo izraz \frac{1}{n} de^{T}, gdje je e jedinični vektor stupac, a vektor d vektor stupac koji na i-tom elementu ima jedinicu ako je i-ti redak matrice Q nul-redak, a inače ima nulu [1].

Tada za Primjer 1 vrijedi:

Za graf G' kažemo da je podgraf grafa G, ako je skup vrhova grafa G' podskup skupa vrhova grafa G i skup bridova grafa G' podskup skupa bridova grafa G. U grafu mogu postojati podgrafovi koji su izolirani, tj. nemaju bridova prema niti jednom drugom vrhu grafa. To znači da imamo skup stranica koje mogu pokazivati jedna na drugu, ali nisu nikako povezane s drugim stranicama u mreži. U tom slučaju će šetač ostati zarobljen u takvom podgrafu. U Primjeru 1 će do toga doći ako šetač ode na stranicu C, jer nakon toga može završiti samo u stranici C ili D, jer ne postoji poveznica iz vrhova C i D u vrhove A i B.

Problem izoliranih podgrafova povezuje se s problemom reducibilnosti matrice. Matrica A\in \mathbb{C}^{n\times n}, n\geq 2 je reducibilna ako postoji matrica permutacije P i p\in \lbrace 1,2, ..., n-1\rbrace tako da vrijedi

Ako je n=1, onda je matrica A reducibilna ako je A = [0]. Matrica je ireducibilna, ako nije reducibilna.

Potrebno je definirati još nekoliko važnih pojmova vezanih uz grafove. Put u grafu od vrha v_{k} do vrha v_{l} je niz usmjerenih bridova v_{k}v_{i1}, v_{i1} v_{i2}, ..., v_{ij-1}v_{l}, pri čemu je j duljina puta. Nadalje, jako povezani graf je graf u kojemu su svaka dva njegova vrha povezana putem. Može se pokazati sljedeća tvrdnja [2]: kvadratna matricaQ je ireducibilna ako i samo ako je njen graf jako povezan.}

Neka matrica Q reprezentira mrežu na dosada opisani način. Ako graf koji reprezentira mrežu ima izolirani podgraf, tada matrica Q ne može biti ireducibilna, jer pripadni graf nije jako povezan. Problem zaglavljenosti u podgrafu rješava se omogućavanjem skoka iz bilo kojeg vrha u bilo koji vrh. Vjerojatnost tog skoka treba biti mala, ali različita od nule. Tome služi faktor prigušenja \alpha \in (0, 1), koji iznosi 0.85 u Googleovom pretraživaču. Kombinacijom rješenja problema zaglavljenosti u vrhu i podgrafu uz \alpha = 0.85 dobivamo novu matricu \tilde{Q}:

Odabirom faktora \alpha se smanjuju svojstvene vrijednosti matrice. To znači da će za mali \alpha doći do brže konvergencije ka konačnom rezultatu. Međutim, mali \alpha znači i da će konačni rezultat algoritma loše prezentirati stvarne vrijednosti, jer se dopušta da nasumični skokovi kojih inače nema uvelike utječu na rezultat. Kod velikog \alpha situacija je obrnuta – algoritam će sporije konvergirati, ali će rezultat biti točniji. Iz navedenih razloga kao dobar odabir za faktor prigušenja, uzima se vrijednost 0.85 [1].

Može se pokazati da matrica koja je redak-stohastička i ireducibilna ima najveću svojstvenu vrijednost 1 i da joj je pripadni svojstveni vektor stupac r jedinstven i nenegativan. Matrica susjedstva je modificirana kako bi riješila neke potencijalne probleme pa je potrebno metodu potencije primijeniti na matricu \tilde{Q}^{T}, tj. iteracije su

Gornja formula se koristi iterativno do konvergencije kako je opisano u Poglavlju 2. Međutim, u praksi matrice koje se koriste su jako velikog reda (milijuni ili milijarde). Zato se umjesto matrice \tilde{Q} može koristiti izraz:

Iterativni postupak koristeći rijetko popunjenu matricu Q uvelike smanjuje vrijeme i memorijski prostor koji je potreban. Važan argument za korištenje metode potencija kako bi se riješio problem PageRanka je činjenica da je to najjednostavnija i vrlo efikasna metoda upravo za rijetko popunjene matrice, a kao rezultat se dobije svojstveni vektor koji pripada najvećoj svojstvenoj vrijednosti. Potrebno je naglasiti da metoda potencije ne mijenja početnu matricu tijekom izvršavanja. Nadalje, može se pokazati da je dovoljno koristiti sljedeći oblik iteracija za metodu potencija [1]:

Bitna prednost navedene formule proizlazi iz činjenice da nije potreban vektor d, tj. nije potrebno znati koje stranice nemaju poveznicu ni na jednu drugu stranicu.

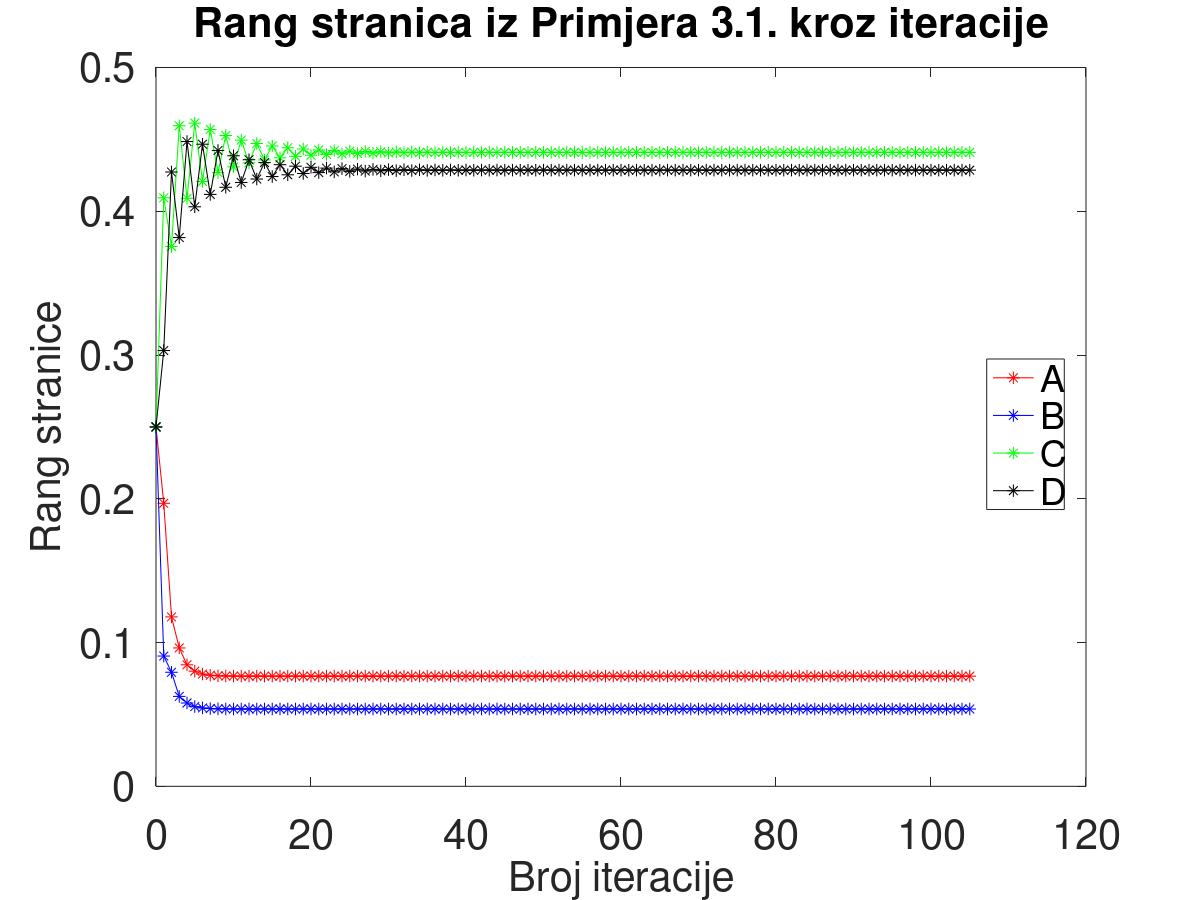
Kombinacijom opisane metode potencija i (4) možemo napisati skriptu u programskom paketu GNU Octave koja implementira računanje ranga internet stranica koristeći PageRank algoritam i metodu potencija kao u skripti 1.

Tablica 1 prikazuje vrijednost ranga stranica i relativnu pogrešku kroz iteracije za odabir eps = 10^{-2}, dok su u tablici 2 rezultati dobiveni za odabir eps = 10^{-8}. Konvergencija se postiže u prvom slučaju nakon 20 iteracija, a u drugom nakon 105 iteracija. Provjerom je utvrđeno da je l_{1} norma vektora r jednaka jedan kroz sve iteracije, što se i očekuje. Nadalje, pripadna svojstvena vrijednost svojstvenog vektora rješenja r bi trebala biti jedan. Provjeru možemo izvršiti pomoću izraza

Uz odabira eps = 10^{-2} dobivamo vektor (1.00000, 1.00000, 1.00834, 0.99150)^{T}, a za eps = 10^{-8} vektor (1, 1, 1,1)^{T}, zaokružimo li rezultate na 5 decimalnih mjesta, što je u skladu s dopuštenom pogreškom i pokazuje da je rješenje s manjom dopuštenom pogreškom točnije i u ovom segmentu.

Slika 5: Graf koji prikazuje vrijednosti ranga pojedinih stranica iz primjera 1 kroz iteracije metode potencija PageRank algoritma za toleranciju 10^{-8}. Vrijednosti ranga se u početku brzo mijenjaju, a onda su promjene u vektoru ranga sve manje dok ne postignemo visoku relativnu točnost.

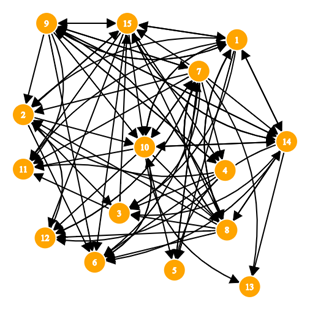
Postoje brojne baze matrica susjedstva za stvarne mreže, a koje su dostupne na internetu. Biblioteka Stanford Network Analysis Project (SNAP) razvija se od 2004. godine i nudi bazu podataka i alate za analizu velikih mreža. Na internetskoj stranici [12] dostupni su podaci o projektima i člancima koji su proizašli radom na ovoj biblioteci.

Kao primjer velike matrice koristit će se Googleova matrica, koja je javno objavljena i korištena na natjecanju iz programiranja 2002. godine. Kao pobjednik tog natjecanja izašao je Daniel Egnor koji je za prvo mjesto osvojio nagradu od 10 000 američkih dolara s projektom „Geografsko pretraživanje“. Više o tom natjecanju možete pročitati u [8]. Matrica je dostupna na stranici SNAP projekta, kao i [13] u raznim formatima. Matrica je reda 916 428, što znači da ima približno 840 milijardi elemenata od čega je različito od nule samo 5 105 039 (\approx 6.1 \cdot 10^{-4} \%). Spremanje svih elemenata matrice u memoriju, uključujući nule, nije moguće. Međutim, matricu je moguće spremiti u formatu rijetko popunjene matrice (engl. sparse matrix). Tada se spremaju samo indeksi elemenata koji nisu nula i njihove vrijednosti u obliku (# retka, # stupca, vrijednost elementa). Ovaj format omogućuje da se prethodna matrica spremi na svega nekoliko desetaka MB memorije, ovisno o formatu. S obzirom da je to matrica susjedstva, potrebno ju je modificirati. Matrica je modificirana u traženi oblik uz pomoć funkcija za rad s rijetko popunjenim matricama. Zatim je metodom potencija izračunat svojstveni vektor r. U Tablici 3. prikazano je deset najbolje rangiranih stranica. Rezultat je uspoređen s rezultatom Matlabove ugrađene funkcije centrality() s istim parametrom a i tolerancijom te je utvrđena relativna pogreška u odnosu na Matlabovo rješenje reda 10^{-12}, što pokazuje da je implementacija uspješna. Matlab bi mogao koristiti drugačiji kriterij zaustavljanja, odakle može doći dominantna pogreška.

Kako bismo ubrzali izvršavanje skripti, možemo koristiti transponiranu matricu Q' kao ulaz u funkciju PageRankMP(), jer tada ne trebamo transponirati matricu Q u svakom koraku metode potencija, već koristimo ulaznu matricu direktno. Algoritam 3 i skripta 3 demonstriraju računanje ranga stranica koristeći PageRank algoritam i metodu potencija. Implementacija je dostupna na GitHub poveznici https://github.com/markohajba/PageRank_PowerMethod.

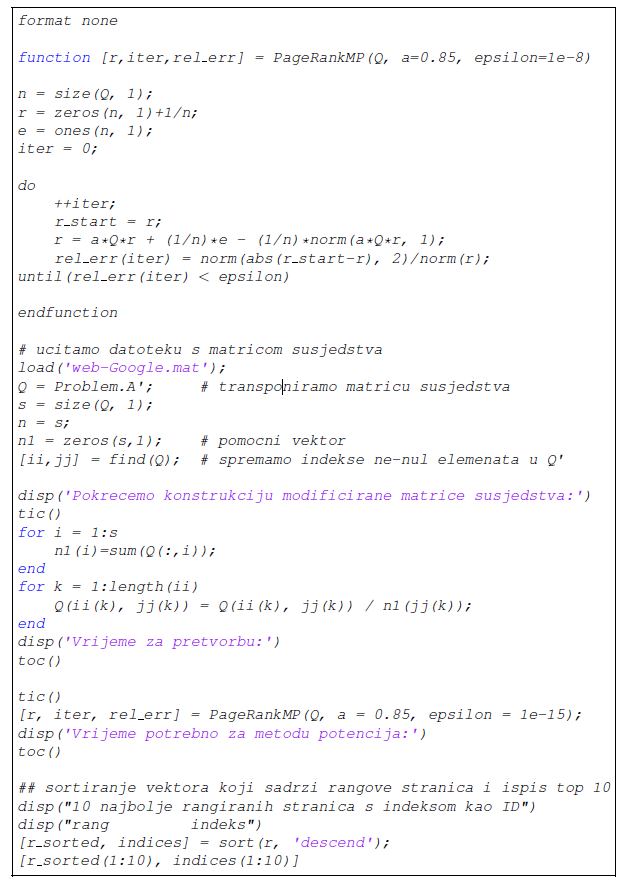
Rad s rijetko popunjenim matricama pokazao se ključan u radu s matricama velikog reda. To nas je motiviralo da dublje istražimo rad s takvim tipom matrica. Jedan od način je generiranje slučajnih matrica susjedstva za željeni broj stranica u mreži. Implementirane su tri metode. Prva metoda, metoda A, koristi ugnježdene petlje i ne koristi funkcije za rad s rijetko popunjenim matricama. Druga metoda, metoda B, koristi funkciju sparse() za koju je potrebno pripremiti argumente ulaza. Treća metoda, metoda C, koristi funkcije sprand() i spones(). Metode koje koriste funkcije za rad s rijetko popunjenim matricama, osim što omogućavaju njihov zapis u slučaju jako velikih dimenzija, daju višestruko ubrzanje njihovog generiranja, a zatim i rada s njima.

Na računalu AIME Workstation A.I. T502 s procesorom Ryzen 9 5900X vrijeme potrebno za generiranje slučajne matrice reda 1000 na jednoj niti procesora metodom A je 63 -64 s, metodom B 0.3-0.4s, a metodom C 0.009 - 0.03 s. Slučajnu matricu istog reda i popunjenosti kao Googleova matrica u 4.2 možemo generirati metodom C za približno 1.6 s. Implementacije metoda dostupne su na GitHub poveznici https://github.com/markohajba/PageRank_PowerMethod.

Slika 7: Prikaz međusobnih poveznica prvih petnaest stranica u slučajno generiranoj matrici susjedstva reda 1000.

PageRank algoritam daje bitan kriterij za rangiranje internetskih stranica u Googleovom internetskom pretraživaču. U radu su dane osnove teorije algoritma koje su potkrijepljene primjerima. U programskom paketu GNU Octave pojašnjena je implementacija algoritma PageRank pomoću metode potencija. Detalji su dani na primjeru male mreže stranica, a zatim je implementacija testirana na matrici visokog reda. Korištenjem funkcija za rad sa rijetko popunjenim matricama, dobiva se značajno ubrzanje izvršavanja algoritma. Točnost dobivenog rješenja za matricu velikog reda provjerena je pomoću Matlabove ugrađene funkcije centrality() i utvrđena je visoka relativna točnost rješenja. Demonstrirano je generiranje slučajnih matrica susjedstva mreže pomoću 3 metode. Dodatno su navedeni izvori gdje se mogu pronaći matrice velikog reda iz stvarnog svijeta. {20}