AlphaZero: strojno učenje podrškom bez domenskog znanja
Algoritam AlphaZero nudi elegantan pristup rješavanju problema igranja igara na ploči, gdje su pravila igre fiksirana, aktualni položaj u igri je u potpunosti poznat te postoji protivnik, kojemu je primarni cilj spriječiti igrača da pobijedi u igri. Postojanje protivnika upravo je ono što takve igre čini kompliciranima—pravila igre obično su dosta jednostavna i kompaktna, ali je otežavajući faktor prisutnost protivnika s nepoznatom strategijom, koji nastoji pobijediti u igri. Preciznije, algoritam AlphaZero pogodan je za tzv. kombinatorne igre za dva igrača, a takve igre imaju sljedeća svojstva:
| \bullet | Sekvencijalnost: igrači, označimo ih sa \operatorname{\textbf{1}} i \operatorname{\textbf{2}}, naizmjenice vuku svoje poteze (akcije). |
| \bullet | Potpuna informacija: oba igrača u svakom trenutku imaju dostupne sve informacije o trenutnom stanju igre. Na primjer, u šahu oba igrača vide pozicije svih figura (i svojih i suparničkih) pa je šah igra s potpunom informacijom. S druge strane, u pokeru igrač ne vidi protivničke karte, pa to nije igra s potpunom informacijom. |
| \bullet | Suma nagrada koje igrači dobiju na kraju igre je jednaka nuli. Na primjer, možemo reći da je nagrada za pobjedu u šahu jednaka 1, za poraz -1, a za remi 0. Drugim riječima, u takvim igrama pobjeda jednog igrača znači poraz drugog. |
| \bullet | Determinizam: za svako stanje igre s i za svaku akciju a koja je dozvoljena u tom stanju postoji jedinstveno novo stanje \tilde{s} = \operatorname{\mathsf{next}}(s, a) u koje igra prelazi nakon što je odigrana akcija a. Drugim riječima, u igri nema faktora slučajnosti. |
Kombinatorne igre se tipično modeliraju pomoću stabla, poput onog prikazanog na slici
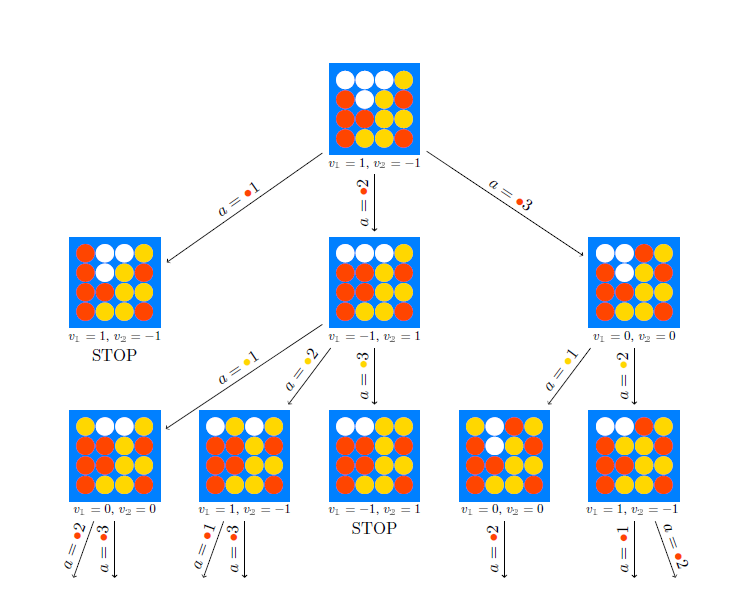
Prirodno pitanje koje si svaki igrač postavlja tijekom igre jest: koja je najveća moguća nagrada koju mogu ostvariti svojim potezima iz stanja s u kojem se igra trenutno nalazi, bez obzira na to kako igra drugi igrač? Tu najveću moguću nagradu zovemo vrijednost stanja s za danog igrača i, te označavamo sa v_{i}(s). Lako se, indukcijskim argumentom počevši od listova stabla, vidi da za svako stanje s vrijedi v_{\operatorname{\textbf{1}}}(s) = -v_{\operatorname{\textbf{2}}}(s). Označimo sa \operatorname{\mathcal{A}}(s) skup dozvoljenih poteza (akcija) koji se smiju napraviti u stanju s, a sa \operatorname{\mathcal{N}}(s) = \lbrace \operatorname{\mathsf{next}}(s, a) : a \in \operatorname{\mathcal{A}}(s) \rbrace skup svih stanja u koja igra može prijeći nakon stanja s. Promotrimo situaciju u kojoj je igrač \operatorname{\textbf{1}} na potezu u igri koja je u stanju s. Njegov optimalni potez vodi ga u stanje u kojem je njegova nagrada najveća moguća, odnosno, vrijedi:
No, na potezu u stanju \tilde{s} je igrač {\operatorname{\textbf{2}}}. Iz njegove perspektive,
pa uvrštavajući u
Iz ove jednakosti slijedi rekurzivni algoritam minimax koji, barem u teoriji, može pronaći pobjedničku strategiju ako ona postoji. Algoritam generira stablo igre, pri čemu korijen opisuje trenutno stanje s u igri, te izračunava vrijednost stanja za svaki čvor koristeći vrijednosti stanja njegove djece i formulu
Kako odrediti aproksimativnu vrijednost nekog stanja? Jedna mogućnost je napraviti jednu ili više simulacija igre od tog stanja nadalje, koristeći pritom neku trivijalnu strategiju (na primjer, u nedostatku bolje ideje, posve slučajno odabirati poteze), te vratiti prosječnu nagradu koju je u svim simulacijama ostvario igrač \operatorname{\textbf{1}}. Alternativno, za konkretnu igru moguće je procijeniti situaciju u kojoj se nalazi igrač: na primjer, u šahu aproksimativna vrijednost stanja bi mogla biti 0.9 ako igrač \operatorname{\textbf{1}} svojim potezom može zaprijetiti šahom, a -0.9 ako je u takvoj situaciji protivnik i slično. Ove ideje navodimo samo za ilustraciju; u praksi se, naravno, koriste nešto složenije aproksimacije.

Pretraživanje stabla Monte Carlo metodom (engl. Monte Carlo Tree Search, MCTS) je alternativna metoda rješavanja problema s prevelikim brojem čvorova u stablu igre. Promotrimo ponovno situaciju u kojoj trebamo odabrati akciju za igrača \operatorname{\textbf{1}} na potezu u stanju s. Umjesto da napravi potpuno stablo igre u čijem korijenu je stanje s, MCTS nastoji usmjeriti izgradnju stabla tako da otkriva stanja za koje je izglednije da imaju veću vrijednost za igrača \operatorname{\textbf{1}}. To se postiže formiranjem vjerojatnosnog modela igre: MCST želi odrediti broj \pi(a) koji predstavlja vjerojatnost da je a \in \operatorname{\mathcal{A}}(s) optimalna akcija za igrača \operatorname{\textbf{1}}. Tu vjerojatnost će aproksimirati statistikom dobivenom simulacijama velikog broja partija koje sve započinju stanjem s. Tijekom simulacija se postupno gradi stablo igre, a akcije u simulacijama se biraju na dva načina, politikom stabla (eng. tree policy) i zadanom politikom (eng. default policy):
| \bullet | Politika stabla definira kako u čvoru u do sada izgrađenog stabla odabrati sljedeću akciju u tijeku jedne simulacije. Odabir sljedeće akcije nas pomiče na dijete tog čvora (ako ono već od ranije postoji u stablu) ili dodaje novi čvor u stablo (ako odabranu akciju nismo proveli niti u jednoj ranijoj simulaciji). |
| \bullet | Zadana politika definira provedbu simulacije od stanja u novododanom čvoru (vidi gornju točku) do završetka igre. Zadana politika ima ulogu koja je analogna heurističkoj aproksimaciji vrijednosti stanja kod algoritma minimax-\ell. |
U svakom čvoru u MCTS stabla čuvamo sljedeće informacije: N(u) je broj simulacija koje su prošle kroz čvor u (tj. simulacija koje su u nekom trenutku bile u stanju iz tog čvora), a Q(u) je suma svih (aproksimacija) vrijednosti stanja \operatorname{\mathsf{state}}(u) u svim simulacijama za onog igrača čiji potez vodi na to stanje. U svakoj simulaciji ove se vrijednosti osvježe za sva stanja kroz koje simulirana igra prođe. Pseudokod osnovnog MCTS algoritma je dan u Algoritmu

Preostaje još pitanje kako implementirati politiku stabla. Jasno je da su, iz perspektive igrača koji je na potezu u stanju \operatorname{\mathsf{state}}(u), perspektivnija ona djeca c tog čvora za koja je u ranijim simulacijama ostvario veću prosječnu nagradu \frac{Q(c)}{N(c)}. S druge strane, nužno je povremeno odigrati akciju koja ranije nije bila često ili uopće igrana kako ne bismo propustili otkriti neki novi, obećavajući smjer u igri. Taj balans između iskorištavanja postojeće statistike za maksimizaciju nagrade i istraživanja novih akcija postiže se politikom tzv. gornje pouzdane ograde za stabla (eng. UCT, Upper Confidence Bound for trees): ako sa \operatorname{\mathcal{C}}(u) označimo skup djece čvora u, onda politika stabla UCT odabire onu akciju iz čvora u koja vodi u dijete
Akcije koje su se u prethodnim simulacijama pokazale boljima će imati veći prvi pribrojnik, a akcije koje ranije nisu bile često birane će imati veći drugi pribrojnik; tipična vrijednost koeficijenta \alpha je \sqrt{2}. Teorijsko opravdanje formule
Nakon što je napravljen dovoljan broj simulacija, igrač \operatorname{\textbf{1}} treba odabrati akciju dozvoljenu u stanju zapisanom u korijenu MCTS stabla. To se najčešće obavlja na jedan od sljedećih načina:
| \bullet |
Odaberi akciju koja vodi na dijete c s najvećom prosječnom nagradom \frac{Q(c)}{N(c)}, odnosno, dijete koje daje formula |
| \bullet | Odaberi akciju koja vodi na najčešće posjećeno dijete korijena (tzv. robusno dijete). Ako sa \operatorname{\mathsf{child}}(u, a) označimo dijete čvora u do kojeg vodi akcija a, onda je logika iza ovog odabira u modeliranju vjerojatnosti poduzimanja akcije a sa \pi(a) \approx \frac{N(\operatorname{\mathsf{child}}(u, a))}{\sum_{c \in \operatorname{\mathcal{C}}{(u)}}N(c)}. |
Nakon što i protivnički igrač odigra svoj potez, igrač \operatorname{\textbf{1}} bi mogao graditi posve novo MCTS stablo s korijenom u novonastaloj situaciji. Bolji pristup je zadržati odgovarajuće podstablo postojećeg MCTS stabla jer ono već sadrži dio statistike za simulacije iz prethodnog stanja igre.
Najizraženiji problem koji preostaje u algoritmu opisanom u prethodnoj cjelini je definicija smislene zadane politike, odnosno, što bolje aproksimacije vrijednosti stanja za listove do sada izgrađenog MCTS stabla. AlphaZero taj problem rješava korištenjem duboke neuronske mreže f_{\theta}. Implementacija iz
Vektor politike svakoj akciji a pridružuje vjerojatnost \hat{\pi}(a) odigravanja te akcije u stanju s; uočimo analogiju ove ideje s motivacijom za algoritam MCTS. Neuronska mreža izgrađuje svoj vjerojatnosni model igre temeljem vjerojatnosti \hat{\pi}, dok istovremeno MCTS algoritam izgrađuje svoj model temeljem vjerojatnosti \pi. Cilj treniranja neuronske mreže je da, osim dobivanja što realnijih aproksimacija vrijednosti stanja koje odgovaraju stvarnim ishodima igara, izgradi vjerojatnosni model koji se podudara s onim dobivenim MCTS stablom.
Opišimo sada proces treniranja neuronske mreže, čiji pseudokod je prikazan i u Algoritmu
Ovdje su c_{\text{base}} i c_{\text{init}} konstante; vidimo da je izbor akcije koja ranije nije bila često birana dodatno ponderiran s vjerojatnosti koju joj je pridružila neuronska mreža. Po izgradnji stabla, MCST algoritam vraća procjenu vjerojatnosti odigravanja pojedinih akcija iz korijena stabla (označimo ga s k) u obliku vektora \pi_{t},
Ovdje je \tau tzv. parametar temperature koji se u prvih nekoliko (na primjer, 10) poteza svake igre postavlja na 1, a zatim se uzima \tau \to 0. U stanju s_{t} program će slučajno odabrati neku akciju a s vjerojatnosti \pi_{t}(a), te ju odigrati—uočimo da izbor parametra temperature ima za posljedicu to da je u početku igre vjerojatnost odabira akcije proporcionalna posjećenosti djeteta korijena MCTS stabla, dok se kasnije uvijek odabire najposjećenije (robusno) dijete. Pripadno podstablo MCTS stabla izgrađenog za stanje s_{t} zadržava se i u narednom koraku.
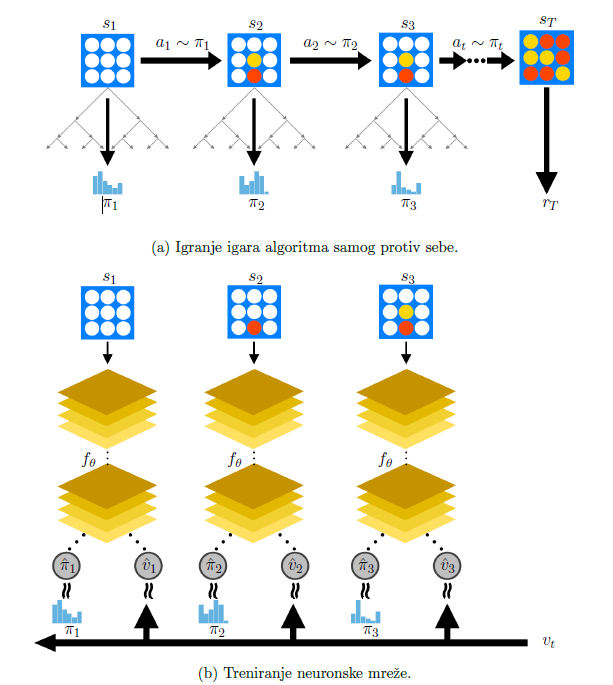
Igra završava u koraku T, kada se dosegne završno stanje s_{T}, a kojemu pripada nagrada r_{T}. Iz svakog pojedinog koraka 1\le t \lt T pohranjuje se uređena trojka (s_{t},\pi_{t},v_{t}), gdje je v_{t} = \pm r_{T} nagrada iz perspektive igrača koji igru dovodi u stanje s_{t}. Po završetku iteracije i, novi parametri neuronske mreže \theta_{i} dobivaju se treniranjem neuronske mreže na temelju primjera za učenje oblika \left(s, \pi, v\right), dobivenih uzimanjem uzorka iz diskretne uniformne distribucije na skupu uređenih trojki (s_{t}, \pi_{t}, v_{t}) iz svih koraka t svih odigranih igara u iteraciji i. Ažurirani parametri \theta_{i} potom se koriste u igrama algoritma samog protiv sebe u narednoj iteraciji (odnosno, kao zadana politika u narednoj iteraciji).
Samo treniranje na temelju primjera \left(s, \pi, v\right) provodi se ovako: neuronska mreža se evaluira za ulaz s, te vraća (\hat{v}, \hat{\pi}) = f_{\theta}(s), a njezini parametri \theta se ažuriraju s ciljem minimizacije funkcije greške (eng. loss function)
Analizirajmo malo gornji izraz. Primjer \left(s, \pi, v\right) predstavlja jedan ishod odigrane igre koja je prošla kroz stanje s: ona je završila nagradom v, a MCTS stablo je procijenilo vjerojatnosti akcija vektorom \pi. S druge strane, neuronska mreža će aproksimirati vrijednost tog stanja sa \hat{v}, a vjerojatnosti vektorom \hat{\pi}. Minimizacijom prvog pribrojnika u
koja postiže minimum (za fiksni \pi) kada je \hat{\pi} = \pi, pa je cilj minimizacije funkcije L postići da neuronska mreža daje što sličniju prognozu vjerojatnosti igranja pojedinih akcija kao što ih daje MCTS stablo. Treći pribrojnik u

Opisani proces učenja ilustriran je slikom
Za ilustraciju algoritma AlphaZero, napravili smo implementaciju za igru Connect Four pomoću programskog jezika Python i dodatnih biblioteka za njega. Vjerujemo da su čitatelji upoznati s ovom igrom, no opišimo ju ukratko. Connect Four je društvena igra za dva igrača, u kojoj je svakome od njih dodijeljena jedna boja (žuta ili crvena) te u kojoj oni naizmjence ubacuju diskove pripadajuće boje u rešetku, obično sa šest redaka i sedam stupaca. Kada dođe red na pojedinog igrača, on mora ubaciti disk svoje boje u neki od stupaca rešetke s barem jednim praznim mjestom. Kada jedan od igrača ubaci disk u rešetku, disk upada u nju na najniže slobodno mjesto—diskovi ubačeni u isti stupac slažu se vertikalno jedan na drugog. Cilj pojedinog igrača je biti prvi koji će formirati vodoravni, okomiti ili dijagonalni niz od četiri diska svoje boje.

Igru Connect Four intuitivno bismo mogli okarakterizirati kao jednostavnu—pogotovo ako ju promatramo u odnosu na kompleksne igre poput igre Go. Međutim, ukupan broj različitih stanja igre, prema
Arhitektura neuronske mreže za algoritam AlphaZero je skicirana na slici
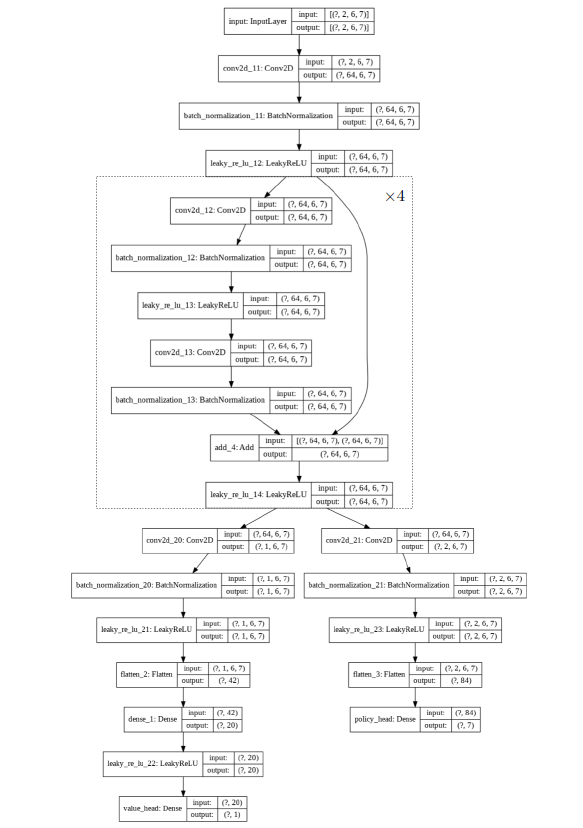
Proces treniranja izvršavan je na računalnom klasteru Isabella smještenom u Sveučilišnom računskom centru Sveučilišta u Zagrebu (SRCE). Isabella se sastoji od 135 računalnih čvorova, koji sadrže 3100 procesorskih jezgri i 12 grafičkih procesora, te je zajednički resurs svih znanstvenika u Hrvatskoj. Svaki proces učenja izvodili smo samo na jednom specijaliziranom čvoru tipa Dell EMC PowerEdge C4140, pomoću jednog od četiri dostupna grafička procesora NVIDIA Tesla V100-SXM2-16GB. Program je izvršavan nekoliko dana (oko 100 sati), a tijekom izvršavanja obavljeno je 150 iteracija algoritma.
Tijekom učenja težine modela pohranjuju se svaki put kad se neuronska mreža dobivena treniranjem unutar pojedine iteracije pokaže boljom od najuspješnije neuronske mreže. Dvije mreže, odnosno, pripadne agente, uspoređujemo tako da odigraju jedna protiv druge određen broj igara, a novu mrežu proglašavamo boljom ako pobijedi dosad najbolju mrežu u 55% tih igara. Na taj način smo nakon 150 iteracija dobili niz od ukupno 57 neuronskih mreža (i pridruženih agenata) stvorenih u različitim trenucima učenja, koji stoga imaju različitu uspješnost u igranju igre. Očekujemo da su agenti čije su neuronske mreže nastale u kasnijim trenucima učenja uspješniji od onih kojima odgovaraju ranije neuronske mreže.
Napredak tijekom učenja praćen je mjerenjem uspješnosti pojedinih agenata u igrama protiv sljedećih algoritama za igranje igre Connect Four:
| \bullet | nasumični (engl. random) algoritam: algoritam koji definira agenta koji u svakom stanju o akciji odlučuje potpuno slučajno. Za dano stanje određuje koje su akcije u njemu legalne te nasumično odabire jednu od njih; |
| \bullet |
minimax-\ell, za razne vrijednosti \ell, čiju implementaciju smo preuzeli iz |
| \bullet | agenti nastali u drugim iteracijama treniranja algoritma AlphaZero. |
Slika
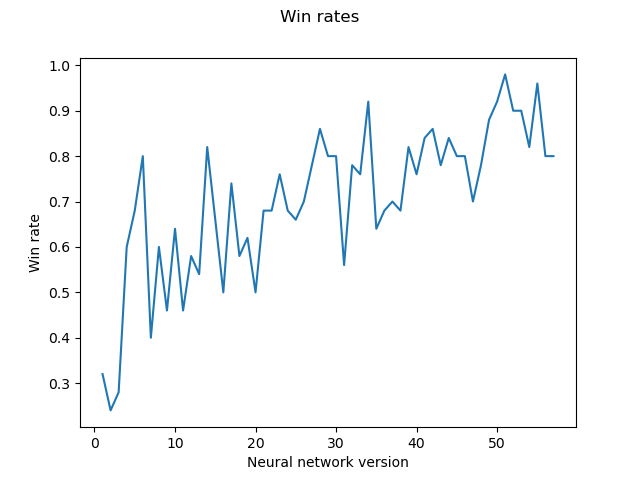
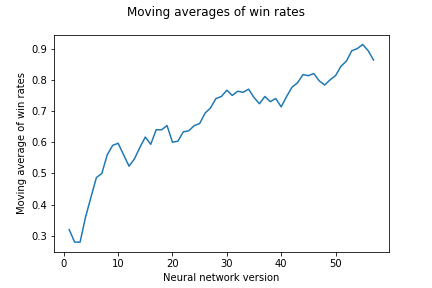
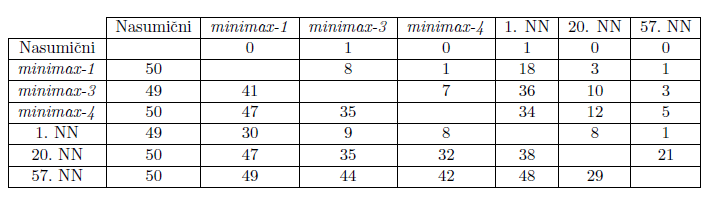
Napredak tijekom učenja utvrđujemo i promatranjem rezultata igara u kojima suprotstavljamo sve verzije AlphaZero agenata jedne protiv drugih. Održavamo “turnir” u kojemu svaki AlphaZero agent igra 2 igre protiv svakog drugog. Sada svakom agentu za svaku pobjedu dajemo jedan bod, a za svaki poraz oduzimamo jedan bod. Budući da imamo ukupno 57 AlphaZero agenata, maksimalan broj bodova koji je moguće ostvariti je 112, a minimalan -112. Na slici
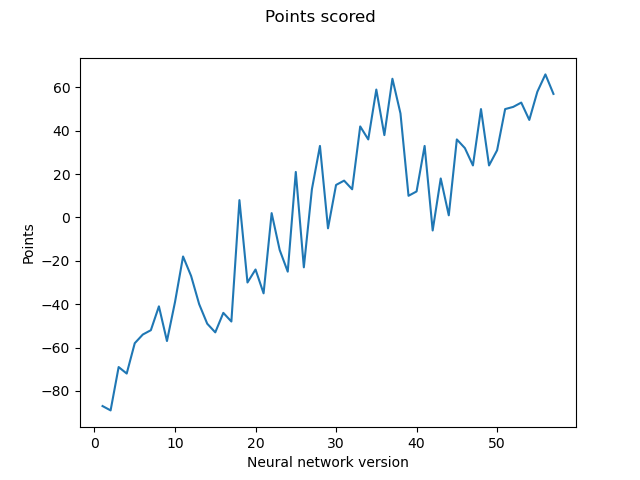
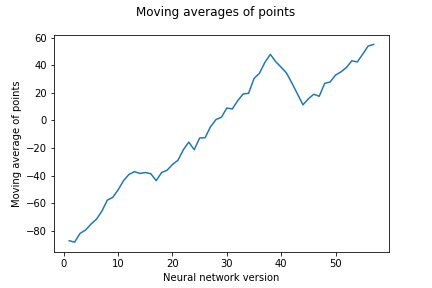
Konačno, uspješnost raznih agenata za igru Connect Four uspoređujemo ispunjavanjem tablice
U ovom članku smo opisali arhitekturu algoritma AlphaZero, koja je svojim spojem Monte Carlo stabla pretraživanja i duboke neuronske mreže donijela revoluciju u sposobnosti umjetne inteligencije za igranje kombinatornih igara. Iako je igra Connect Four na kojoj smo ilustrirali ovaj algoritam jednostavna u usporedbi s šahom ili igrom Go, a računalni hardver na kojem je izvršeno treniranje za red veličine slabiji od onog pomoću kojeg je DeepMind
| [1] | The on-line encyclopedia of integer sequences: Number of legal 7 x 6 Connect-Four positions after n plies. https://oeis.org/A212693. |
| [2] | Martin Abadi, Ashish Agarwal, Paul Barham, Eugene Brevdo, Zhifeng Chen, Craig Citro, Greg S. Corrado, Andy Davis, Jeffrey Dean, Matthieu Devin, Sanjay Ghemawat, Ian Goodfellow, Andrew Harp, Geoffrey Irving, Michael Isard, Yangqing Jia, Rafal Jozefowicz, Lukasz Kaiser, Manjunath Kudlur, Josh Levenberg, Dandelion Mané, Rajat Monga, Sherry Moore, Derek Murray, Chris Olah, Mike Schuster, Jonathon Shlens, Benoit Steiner, Ilya Sutskever, Kunal Talwar, Paul Tucker, Vincent Vanhoucke, Vijay Vasudevan, Fernanda Viégas, Oriol Vinyals, Pete Warden, Martin Wattenberg, Martin Wicke, Yuan Yu, and Xiaoqiang Zheng. TensorFlow: Large-scale machine learning on heterogeneous systems. https://www.tensorflow.org/, 2015. |
| [3] | C. B. Browne, E. Powley, D. Whitehouse, S. M. Lucas, P. I. Cowling, P. Rohlfshagen, S. Tavener, D. Perez, S. Samothrakis, and S. Colton. A survey of Monte Carlo tree search methods. IEEE Transactions on Computational Intelligence and AI in Games, 4:1–43, 2012. |
| [4] | François Chollet et al. Keras. https://keras.io, 2015. |
| [5] | Alexis Cook. Intro to game AI and reinforcement learning, lesson 3: N-step lookahead. https://www.kaggle.com/alexisbcook/n-step-lookahead . |
| [6] | Aurélien Géron. Hands-On Machine Learning with Scikit-Learn and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems. O'Reilly Media, Inc., 2nd edition, 2019. |
| [7] | L. Kocsis and C. Szepesvári. Bandit based Monte-Carlo planning. In J. Furnkranz, T. Scheffer, and M. Spiliopoulou, editors, Machine Learning: ECML 2006, pages 282–293. Springer, Berlin, Heidelberg, 2006. |
| [8] | L. Kocsis, C. Szepesvári, and J. Willemson. Improved Monte-Carlo search. Univ. Tartu, Estonia, Tech. Rep. 1, http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.374.1202&rep=re... , 2006. |
| [9] | M. Lapan. Deep Reinforcement Learning Hands-On - Second Edition. Packt Publishing, Birmingham, UK, 2020. |
| [10] | Jelena Lončar. AlphaZero: strojno učenje podrškom bez domenskog znanja. Diplomski rad, PMF - Matematički odsjek, https://repozitorij.pmf.unizg.hr/islandora/object/pmf:9349 , 2020. |
| [11] | Julian Schrittwieser, Ioannis Antonoglou, Thomas Hubert, Karen Simonyan, Laurent Sifre, Simon Schmitt, Arthur Guez, Edward Lockhart, Demis Hassabis, Thore Graepel, Timothy Lillicrap, and David Silver. Mastering Atari, Go, chess and shogi by planning with a learned model. Nature, 588:604–609, 2020. |
| [12] | D. Silver, A. Huang, C. Maddison, A. Guez, L. Sifre, G. Driessche, J. Schrittwieser, I. Antonoglou, V. Panneershelvam, M. Lanctot, S. Dieleman, D. Grewe, J. Nham, N. Kalchbrenner, I. Sutskever, T. Lillicrap, M. Leach, K. Kavukcuoglu, T. Graepel, and D. Hassabis. Mastering the game of Go with deep neural networks and tree search. Nature, 529:484–489, 01 2016. |
| [13] | D. Silver, T. Hubert, J. Schrittwieser, I. Antonoglou, M. Lai, A. Guez, M. Lanctot, L. Sifre, D. Kumaran, T. Graepel, T. Lillicrap, K. Simonyan, and D. Hassabis. A general reinforcement learning algorithm that masters chess, shogi, and Go through self-play. Science, 362:1140–1144, 12 2018. |
| [14] |
D. Silver, T. Hubert, J. Schrittwieser, I. Antonoglou, M. Lai, A. Guez, M. Lanctot, L. Sifre, D. Kumaran, T. Graepel, T. P. Lillicrap, K. Simonyan, and D. Hassabis. Mastering chess and shogi by self-play with a general reinforcement learning algorithm. CoRR, abs/1712.01815, 2017. |