Kolaborativno filtriranje
| Riječani 73 |
| 33515, Orahovica |
| m.mirna08@gmail.com (M. Marković) |
| Odjel za matematiku |
| Sveučilište Josipa Jurja Strossmayera u Osijeku |
| Trg Lj. Gaja 6 |
| 31000, Osijek |
| ztomljan@mathos.hr (Z. Tomljanović) |
Preporuka je, prema definiciji iz
Devedesetih godina prošlog stoljeća trgovine, knjižare i kina pronašli su svoje mjesto u virtualnom svijetu što im je omogućilo veću ponudu proizvoda od one na fizičkim policama (engl. long tail phenomen1).
Veliki broj proizvoda i ograničen prikaz informacija o proizvodima korisnicima je otežao pretragu i odlučivanje o njima. Također, trgovcu u klasičnoj trgovini moguće je postaviti pitanje kako bi nam preporučio proizvod sličan onom koji smo nedavno kupili, ali gotovo je nemoguće bilo postaviti isto pitanje internet trgovini i dobiti željeni odgovor. Već na samom početku razvoja internet trgovina, kina i knjižara bilo je očito da standardni način preporuke i otkrivanja novih stvari ima velike nedostatke i ograničenja, a posebice pri razmjeni novih informacija. Za više informacija vidi
Upravo je to potaknulo istraživače na kreiranje automatiziranih sustava koji bi pomogli korisniku pretražiti proizvode i ubrzati on-line kupnju, a istovremeno bili pouzdani i točni. Kako bi ti sustavi postali što sličniji pravim trgovcima i korisnikovim poznanicima trebali bi naučiti ukus svakog pojedinog korisnika ili prepoznati korisnike sa sličnim ukusom te na temelju tih informacija svakom korisniku pružiti personaliziranu preporuku o onome što bi sljedeće mogao pregledati i kupiti.
Srećom, takvi sustavi su ubrzo razvijeni i danas se nalaze u pozadini gotovo svake internetske trgovine, knjižare, aplikacije za gledanje filmova ili slušanje glazbe. Prilikom posjeta YouTube-u, Amazon-u ili Netflix-u već na početnoj stranici aplikacije prikazuje se sadržaj koji bi nam se mogao svidjeti, a u njihovoj pozadini nalaze se spomenuti sustavi koje nazivamo sustavi za preporuke.
Sustavi za preporuke zajedničko je ime za algoritme koji na temelju informacija o korisnicima i proizvodima daju korisnicima preporuke za nove proizvode koji bi im se mogli svidjeti. Dvije su osnovne kategorije sustava za preporuke, kolaborativno filtriranje (engl. collaborative filtering, u nastavku CF sustavi) i kontekstno bazirani sustavi za preporuke (engl. content based, CB). Algoritmi iz skupine kontekstno baziranih sustava za preporuke stvaraju preporuku na temelju proizvoda koje je korisnik kupio ili pozitivno rangirao te preporučuju proizvode sličnoga tipa. Suprotno tome, sustavi za preporuke bazirani na kolaborativnom filtriranju stvaraju preporuku na temelju usporedbe s ostalim korisnicima i preporučuju proizvode koje su njemu slični korisnici kupili ili pozitivno rangirali. Kombinaciju kontekstno baziranih sustava i kolaborativnog filtriranja nazivamo hibridni sustavi za preporuke.
Povijesno gledano, možemo reći da je začetnik automatiziranih sustava za preporuke Grundy, računalni program za knjižnicu (1979. godine) (za više informacija vidjeti
Ovaj rad baziran je na diplomskom radu
Sustavi za preporuke razvijeni su kako bi se što bolje suočilo s eksponencijalnim rastom informacija, u smislu filtriranja podataka. Oni uče iz akcija korisnika o njihovom ukusu kako bi im u skladu s tim predložili nove proizvode, stoga ih istovremeno možemo promatrati kao dio rudarenja podataka i strojnog učenja. Području rudarenja podataka pripadaju zbog svoje namjene, olakšavaju korisniku pretraživanje podataka, a u područje strojnog učenja možemo ih smjestiti jer na temelju podataka o korisniku i proizvodima, uče o njima i prema tome generiraju preporuke.
Iako se sustavi za preporuke intenzivno razvijaju već tridesetak godina, tehnike koje se koriste u algoritmima za generiranje preporuke ostale su relativno jednostavne. Kako bismo objasnili tehnike korištene u algoritmima za preporuke i same algoritme potrebno je prvo navesti osnovne pojmove koji se u njima koriste. Korisnici i proizvodi su dvije osnovne klase entiteta i povezani su tako da korisnici imaju preferencije prema određenim proizvodima, a o njima se zaključuje iz podataka o korisniku ili ih daju sami korisnici. Podatci o vezi korisnika i proizvoda spremaju se u matricu koju nazivamo matrica korisnosti (engl. utility/rating matrix), vidi Tablicu
| Proizvod 1 | Proizvod 2 | Proizvod 3 | Proizvod 4 | |
| Korisnik 1 | 4 | ? | 3 | 5 |
| Korisnik 2 | ? | 5 | 4 | ? |
| Korisnik 3 | 5 | 4 | 2 | ? |
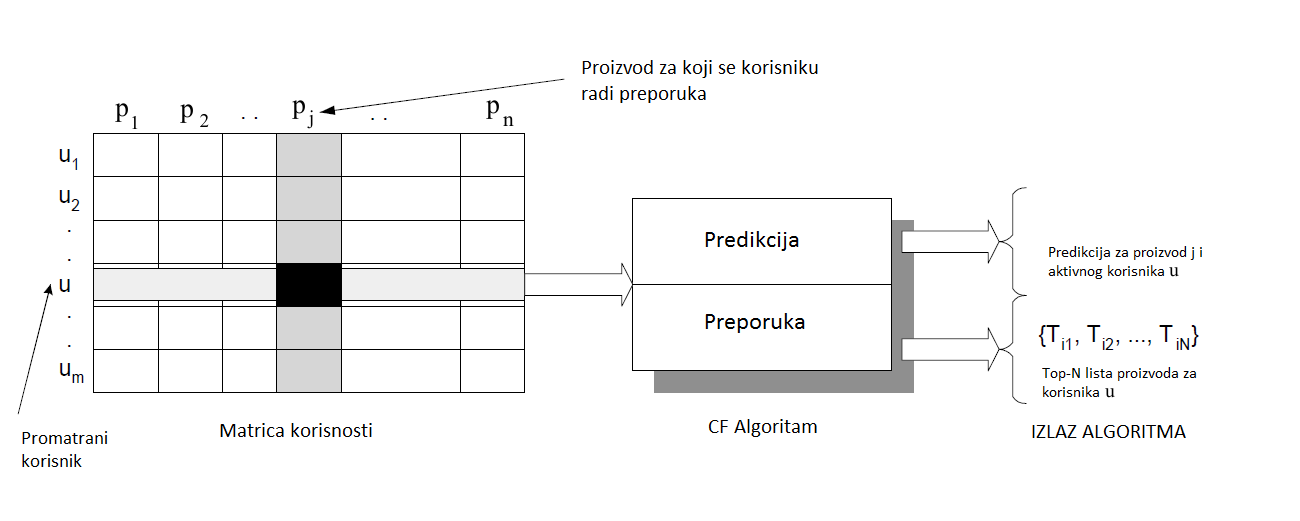
Svaki element matrice korisnosti predstavlja jedan par korisnik-proizvod i on označava razinu koliko se promatranom korisniku sviđa dani proizvod. Razina sviđanja najčešće se prikazuje vrijednostima iz uređenog skupa elemenata kao što su prirodni brojevi od 1 do 5 koji mogu predstavljati rangiranje proizvoda zvjezdicama. Također, moguće je koristiti binarnu ili ternarnu skalu5, dok je unarna skala najbolja za sustave internet trgovina jer jasno predstavlja povijest korisnikove kupnje. Ako korisnik i proizvod nisu povezani tada se na pripadnom mjestu u matrici nalazi nepoznata vrijednost, odnosno ne postoji izražen stupanj sviđanja korisnika prema proizvodu. Pretpostavka je da je matrica korisnosti rijetko popunjena matrica (engl. sparse matrix), a glavni cilj sustava je predvidjeti vrijednosti na praznim mjestima u matrici korisnosti, što je prikazano na Slici
Pri modeliranju sustava za preporuke mogu se promatrati i svojstva proizvoda te iz tih sličnosti predvidjeti vrijednosti na praznim mjestima matrice korisnosti. Vrlo je bitno da nije potrebno izračunati svaku nepoznatu vrijednost u matrice korisnosti, nego je dovoljno otkriti samo neke vrijednosti za svaki redak, koje bi potencijalno mogle biti velike. Točnije, kako je navedeno u
Dvije su osnovne vrste sustava za preporuke, kontekstno bazirani i kolaborativno filtriranje.
Kontekstno bazirani sustavi za preporuke generiraju preporuke tako da za svakog korisnika pronalaze proizvode slične onima koje je korisnik pregledao ili kupio i takvi proizvodi postaju dobri kandidati za preporuku. Kod ovakvih sustava rangiranje je manje bitno, puno je bitnije pronaći sličan sadržaj u skupu svih proizvoda. Ukoliko je takav sustav namijenjen npr. internet videoteci on će generirati preporuke korisniku s obzirom na žanr filmova koje je već pogledao i preporučiti mu bliske filmove. Tehnika kojom se pronalaze slični proizvodi u skupu svih proizvoda jest TF-IDF (engl. term frequency – inverse document frequency) koja predstavlja mjeru koliko je važan neki izraz u skupu dokumenata i ovdje se koristi kako bi sustav mogao zaključiti o ukusu pojedinog korisnika iz njegovih akcija. U takvom sustavu svaki korisnik se promatra kao vektor čiji elementi predstavljaju svojstva proizvoda u sustavu. Vrijednost svakog elementa u tom vektoru su težine za pripadno svojstvo u odnosu na promatranog korisnika.
Dobar primjer domene koja koristi kontekstno bazirani sustav jest pandora.com. Ovakvi sustavi za preporuke korisniku uzastopno preporučuju proizvode koji su slični po svojstvima, što je ujedno njihova prednost i mana (engl. over-specialized search)6. Korisnik mora na neki način sam pokazati interes prema nekom novom tipu proizvoda kako bi mu sustav u buduće mogao preporučiti proizvode s tim svojstvima, što nije slučaj kod kolaborativnog filtriranja. Kod sustava za preporuke baziranih na kolaborativnom filtriranju preporuke se generiraju na temelju korisnikova rangiranja proizvoda, a ne na temelju svojstava proizvoda. Kako je navedeno u
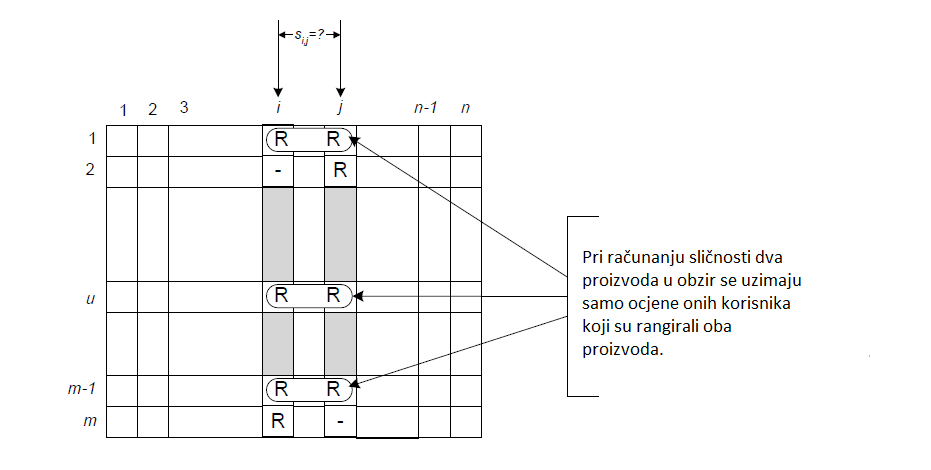
Glavna pretpostavka na kojoj se temelje svi CF sustavi jest da ukoliko isti proizvod dva korisnika isto rangiraju, oni će vjerojatno dijeliti isto mišljenje o još nekim proizvodima. Odnosno, ako se jednom od dva slična korisnika sviđa neki proizvod za koji drugi korisnik ne zna, prethodna tvrdnja govori da taj proizvod možemo preporučiti drugom korisniku i on će mu se vjerojatno svidjeti. Sličnost korisnika ili proizvoda računa se unaprijed definiranom funkcijom koju nazivamo funkcija sličnosti (engl. similarity function), a skup najsličnijih korisnika ili proizvoda u odnosu na promatranog korisnika ili proizvod nazivamo susjedstvo (engl. neighbourhood). Zadaća funkcije sličnosti je da numerički predstavi udaljenost između dva korisnika ili proizvoda kako bi se moglo definirati njihovo susjedstvo, odnosno najbliži korisnici ili proizvodi. Neke od najčešće korištenih funkcija sličnosti su euklidska udaljenost, Pearsonova korelacija i kosinus udaljenost. CF sustavi koji se baziraju na pronalasku sličnih korisnika za nekog promatranog korisnika nazivamo sustavi orijentirani prema korisniku (engl. user based), dok CF sustave koji pronalaze slične proizvode za neki promatrani proizvod nazivamo sustavi orijentirani prema proizvodu (engl. item based).
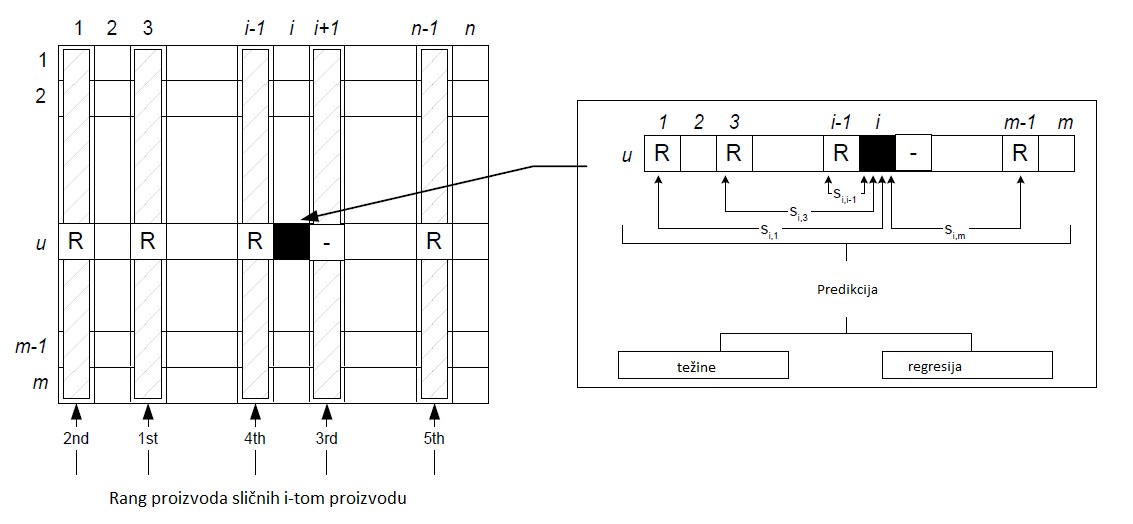
Algoritmi CF sustava orijentirani prema korisniku vode se pretpostavkom da “slični korisnici vole slične proizvode”, dok se oni orijentirani prema proizvodu vode se pretpostavkom da “slične proizvode vole slični korisnici”, kao na Slici
Iako su ova dva pristupa vrlo slična, ovisno o sustavu unutar kojeg su implementirani mogu uvelike utjecati na njegovu skalabilnost7. Ukoliko promatramo sustav sa puno većim brojem korisnika od broja proizvoda, algoritmi orijentirani prema korisniku su loš odabir jer će pronalazak najbližih susjeda biti puno teži u dimenziji korisnika nego što bi mogao biti u dimenziji proizvoda, kojih je manje u bazi. Nadalje, može se reći da je dimenzija korisnika najčešće više dinamička od dimenzije proizvoda, odnosno skup korisnika se češće mijenja od skupa proizvoda, pa je pouzdanije računati sličnosti unutar skupa proizvoda. No, ako promatramo sustav za preporuke u sklopu internetskih novina, tada se skup proizvoda (novosti) sigurno češće mijenja i veći je od skupa korisnika i u tom slučaju algoritmi orijentirani prema korisniku imaju prednost nad algoritmima orijentiranim prema proizvodu. Još jedna prednost algoritama orijentiranih prema proizvodu jest da korisniku mogu dati jasnije objašnjenje preporuke. Činjenica da je neki proizvod preporučen korisniku jer je sličan ostalim proizvodima koji su mu se svidjeli je korisniku ugodnija od one da je proizvod preporučen jer se svidio sličnom korisniku.
Uz podjelu CF sustava na orijentirane prema proizvodu i orijentirane prema korisniku, CF sustave možemo podijeliti na one bazirane na modelu (engl. model based) i memorijski bazirane (engl. memory based).
Memorijski baziranima CF sustavima smatramo one kod kojih algoritam računa sličnosti u memoriji, bez prethodno generiranog modela i često se za njih kaže da su bazirani na susjedstvu (engl. neighbourhood based) jer u skupu najboljih susjeda pronalaze najbolje kandidate. Takvi algoritmi podatke o korisnicima i proizvodima drže u memoriji i direktno računaju preporuke, odnosno sličnost među susjedstvom računa se svaki put kada se korisniku želi dati preporuka, još se kaže da je to on-line generiranje preporuke.
CF sustavi bazirani na modelu generiraju model sustava i na temelju njega generiraju preporuku. Kod pristupa baziranom na modelu kažemo da se model kreira off-line odnosno unaprijed, a preporuka se generira on-line na temelju modela. Ova vrsta algoritma doživjela je procvat tijekom istraživanja za Netflix prize 2006. godine, a pobjednički algoritam koristio je tehniku baziranu na modelu. Pri generiranju modela koristi se faktorizacija matrice korisnosti korisnika i proizvoda na dvije matrice u kojima je moguće zaključiti o nekim skrivenim faktorima u sustavu (npr. žanr filma), ali ti faktori često nisu izravno povezani sa stvarnim svojstvima proizvoda ili korisnika. Iako imaju dosta nedostataka, danas su najviše koriste CF sustavi bazirani na modelu koji koriste faktorizaciju matrice korisnika i proizvoda za kreiranje modela. Najveći nedostatak algoritama baziranih na modelu jest da bi se model trebao računati svaki puta kada dođe do veće promjene u početnoj matrici, odnosno svaki puta kada korisnik rangira neki od proizvoda ili se doda novi korisnik u sustav.
Sustavi za preporuke mogu imati vrlo veliku ulogu u marketingu organizacije koja ga koristi, ukoliko je on pouzdan i brzo daje preporuke visoke kvalitete. Može se reći da je porast dobiti organizacije koja koristi sustav za preporuke poželjna posljedica točnih i brzih preporuka. Takvi sustavi najčešće su integrirani u okruženjima s mnogo korisnika i proizvoda zbog čega naizgled laki zadatci postaju vrlo zahtjevni, a primjer tome su domene kao što su Youtube, Netflix, Amazon, eBay8 i slično.
U stvarnim primjerima i primjenama sustavi za preporuke se moraju nositi s različitim problemima, a istaknuli bismo neke od njih: slaba popunjenost podataka, sinonimi, gray sheep i shilling attacks. Više detalja vezano za spomenute probleme može se pronaći u
U okviru ovog rada istaknuli bismo da se slaba popunjenost podataka pojavljuje jer najčešće matrice sustava su vrlo velikih dimenzija zbog mnogo korisnika i proizvoda u okruženju. No, veliki broj korisnika i proizvoda nisu povezani pa su te matrice najčešće jako slabo popunjene (engl. extremely sparse). Slaba popunjenost najveći problem predstavlja pri dodavanju novog korisnika u sustav (engl. cold start problem), tj. kada korisnik još nema niti jedan rangiran proizvod i nema dovoljno informacija o njemu (engl. new user problem). Također, ako se doda novi proizvod, nemoguće je predložiti ga kao preporuku ukoliko ga nitko još nije rangirao (engl. new item problem). Problem popunjenosti podataka može se riješiti smanjenjem dimenzije sustava, a najčešće korištena tehnika za to je SVD dekompozicija matrice sustava.
Nadalje, problem skalabilnosti sustava za preporuke nastaje ukoliko broj korisnika i proizvoda jako brzo raste. Primjerice, za sustav sa deset milijuna korisnika (M) i milijun proizvoda (N), kada bi CF algoritam bio složenosti O(N) on bi bio prespor uzimajući u obzir da algoritam mora raditi jako brzo u stvarnom vremenu. Ovaj problem se isto može riješiti redukcijom dimenzije pomoću SVD dekompozicije. Problem nastaje kod dodavanja novog korisnika ili podataka u matricu, jer ono zahtijeva ponovno računanje dekompozicije dopunjene matrice, ali i on se može vješto riješiti inkrementalnim računanjem novog modela. Što je sustav brži, to je skalabilnost sustava veća, ali posljedica tome je smanjena kvaliteta preporuke. Upravo je to najveći izazov sustava za preporuke, tj. kako u isto vrijeme zadržati što veću kvalitetu preporuke i povećati skalabilnost sustava.
U sljedećem poglavlju opisat ćemo algoritme za CF sustave bazirane na modelu orijentiranom prema proizvodu koji koriste dekompoziciju na singularne vrijednosti (SVD).
Prije nego što uvedemo dekompoziciju na singularne vrijednosti, prisjetimo se da za matricu Q\in\mathbb{R}^{n\times n} kažemo da je ortogonalna ukoliko je Q^{T}Q = I. Analogno, za U\in \mathbb{C}^{n\times n} kažemo da je unitarna ukoliko je U^{*}U = I.
Dekompozicija na singularne vrijednosti ili SVD (engl. singular value decomposition) je metoda matrične dekompozicije koja danu matricu A \in \mathbb{R}^{m\times n} faktorizira na matrice U \in \mathbb{R}^{m\times m}, S\in \mathbb{R}^{m\times n} i V \in \mathbb{R}^{n\times n} čija su svojstva iskazana Teoremom
U ovom poglavlju iskazat ćemo neke od osnovnih svojstava singularne dekompozicije matrice, a više detalja može se pronaći u
Stupce matrice U zovemo lijevi, a stupce matrice V desni singularni vektori matrice A, dok dijagonalne elemente matrice S nazivamo singularnim vrijednostima.
Poznato je da koristeći SVD dekompoziciju možemo efikasno odrediti rang matrice kao i prostor koji razapinje sliku, odnosno jezgru matrice. Naime, prema
| (1) | rang matrice A je r, tj. \text{rang}(A)=r, |
| (2) | \mathcal{R}(A) = \text{span}(u_{1},\ldots,u_{r}), odnosno, stupci matrice U, u_{1},\ldots,u_{r} razapinju sliku9 od A |
| (3) | \mathcal{N}(A) = \text{span}(v_{r+1},\ldots,v_{n}), odnosno, stupci matrice V, v_{r+1},\ldots,v_{n} razapinju jezgru10 od A |
Prema
Matrica A_{k} dobivena je korištenjem trojki (u_{i}, \sigma_{i},v_{i}^{T}), i=1,\dots,k koje pripadaju najvećim singularnim vrijednostima. Ona daje aproksimaciju matrice A matricom ranga k. Štoviše, to je najbolja aproksimacija nižeg ranga u skupu matrica ranga manjeg ili jednakog k, za bilo koju unitarnu invarijantnu normu11. Specijalno, ako pogrešku mjerimo u Frobeniusovoj normi (\Vert \cdot\Vert _{F}), vrijedi da je:
Ovaj teorem je od velike važnosti za CF sustave jer omogućuje znatno smanjenje količine podataka koje CF sustav treba obraditi. Umjesto s velikom matricom A reda m \times n sustav može raditi s matricom manjeg ranga A_{k} koja se u faktoriziranom obliku može efikasno zapisati sve dok je k \ll r. Točnije, ovaj teorem daje najbolji mogući način kako se matrica može aproksimirati matricom ranga koji je najviše k.
Matrica S tada se očito aproksimira matricom S_{k} tako da se na dijagonali zadrži najvećih k singularnih vrijednosti, dok se matrice U i V aproksimiraju matricama U_{k} i V_{k}. Matrica U_{k} nastaje zadržavanjem prvih k stupaca iz matrice U, dok zadržavanjem prvih k stupaca matrice V nastaje matrica V_{k} i tada je A_{k}=U_{k}S_{k}V_{k}^{T}.
Jedna od najbitnijih svojstava sustava za preporuke je kvaliteta preporuke. Kvaliteta preporuke može se mjeriti na više različitih načina, a prema
Tip metrike koji će se koristiti ovisi o namijeni sustava za preporuke. Najčešće korištena metrika je prosječna apsolutna pogreška (engl. mean absolute error, MAE), iz skupa metrika obzirom na predikciju, koja računa prosječnu apsolutnu razliku između procijenjene vrijednosti i prave vrijednosti.
Računamo li točnost preporuke za proizvod j, MAE možemo računati po slijedećoj formuli:
Pri tome je m je broj korisnika, sa R označavamo matricu korisnosti sustava, a prediction_{ij} je procjena za element r_{ij} matrice sustava R, odnosno za procjena za i-tog korisnika i j-ti proizvod. Što je vrijednost za MAE manja, to je preporuka točnija, odnosno kvalitetnija. Iako ovakvi tipovi metrike mogu pomoći kako bi se odredila kvaliteta sustava, odnosno njegove preporuke, korisnicima ponekad nisu od velike koristi kao u slučaju kada korisnik želi nekakav novi, neočekivani rezultat preporuke koji nije u skladu s njegovim dotadašnjim preferencijama. Za takve slučajeve mogu se koristiti metrike nekog drugog tipa, a u ovom radu koristi se navedena MAE metrika pri analizi kvalitete preporuke u ovisnosti o parametrima promatranog algoritma.
Standardni algoritmi za preporuke podijeljeni su u dva osnovna koraka. Prvi korak predstavlja off-line izgradnju modela sustava (engl. model-building step), dok drugi korak (engl. execution step) radi on-line i računa preporuke. Prema
Prije iskaza samoga algoritma potrebno je uvesti osnovne oznake:
| \bullet | u_{i} označava i-tog korisnika u sustavu, a p_{j} označava j-ti proizvod u sustavu tako da je i\in\lbrace 1,\ldots,m\rbrace i j\in\lbrace 1,\ldots,n\rbrace. |
| \bullet | R\in\mathbb{R}^{m\times n} označava matricu m korisnika i n proizvoda sa elementima r_{ij} koji predstavljaju numeričku oznaku koliko se korisniku u_{i} sviđa proizvod p_{j}. Ukoliko korisnik nije rangirao neki proizvod, tada se na to mjesto u matrici R dogovorno stavlja 0. |
Za određenog korisnika u_{i} potrebno je kreirati preporuku, odnosno predvidjeti koliko će mu se svidjeti proizvod p_{j}, što se može postići sljedećim postupkom.
Algoritam 1 (prema
| (1) | Konstruirati matricu korisnosti sustava, odnosno matricu R\in\mathbb{R}^{m\times n} koja predstavlja m korisnika i n proizvoda čije elemente označavamo s r_{ij} koji predstavljaju numeričku oznaku koliko se korisniku u_{i} sviđa proizvod p_{j}. | ||||||
| (2) |
Eliminirati nepoznata polja, točnije vrijednosti koje su jednake nuli, u matrici R na sljedeći način:
|
||||||
| (3) | Izračunati SVD dekompoziciju matrice R_{norm}, R_{norm}=USV^{T} gdje su U, S i V redom dimenzija m\times m, m\times n i n\times n. | ||||||
| (4) | Reducirati matricu R_{norm} tako da se zadrži samo k najvećih singularnih vrijednosti, k\ll \text{rang}(R_{norm}) te je tada aproksimacija matrice R_{norm} dana matricom U_{k}S_{k}V_{k}^{T} sa elementima \hat{r}_{ij}, gdje su U_{k}\in\mathbb{R}^{m\times k}, S_{k}\in\mathbb{R}^{k\times k} i V_{k}\in\mathbb{R}^{n\times k} | ||||||
| (5) | Izračunati matrični korijen od S_{k}, \sqrt{S_{k}} te U_{k}\sqrt{S_{k}}^{T} \in \mathbb{R}^{m\times k} koja određuje podatke od m korisnika i \sqrt{S_{k}}V_{k}^{T} \in \mathbb{R}^{k\times n} koja određuje podatke od n proizvoda u k-dimenzionalnom prostoru. Matrica W := \sqrt{S_{k}}V_{k}^{T} dimenzije k\times n, k pseudo korisnika12 i n proizvoda je od velikog značaja jer njezini elementi w_{ij} predstavljaju numeričku oznaku koliko se pseudo korisniku u_{i} sviđa proizvod p_{j} | ||||||
| (6) |
Za promatrani proizvod p_{j} kreiramo njegovo susjedstvo na sljedeći način:
|
||||||
| (7) |
Izračunati predikciju za korisnika u_{i} i proizvod p_{j} prema sljedećoj formuli:
(6)
prediction_{ij} = \frac{\sum_{k=1}^{l} sim_{jk}\cdot(\hat{r}_{ik}+\overline{r_{i}})}{\sum_{k=1}^{l}|sim_{jk}|}.
|
Uočimo da se u 1. i 2. koraku algoritma matrica sustava konstruira i priprema za daljnji postupak normalizacijom. 3. korak algoritma računa SVD dekompoziciju matrice što je moguće zbog Teorema
Prema
Dva su osnovna parametra koja mogu utjecati na kvalitetu ovoga algoritma, a to su: parametar k koji određuje dimenziju reduciranog sustava i parametar l koji određuje dimenziju susjedstva promatranog proizvoda.
Kako je prethodno navedeno, parametar k određuje broj singularnih vrijednosti matrice S koje će se zadržati u matrici S_{k}, odnosno određuje rang matrice R_{k} i broj pseudo korisnika u reduciranom sustavu. Parametar k bira se tako da bude što manji kako bi utjecao na poboljšanje brzine i efikasnosti te ujedno mora biti takav da reducirani sustav zadrži što više svojstava početnog sustava, ali da ne bude preblizak početnom sustavu (engl. overfitting). Fiksiranjem parametra l može se eksperimentom za različite k odrediti onaj koji prema MAE daje najbolju preporuku za dani sustav. Slika
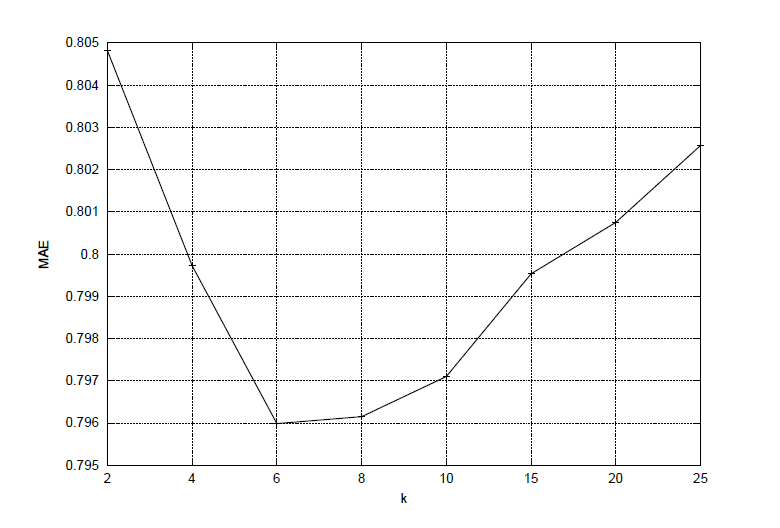
Slika 4: Eksperiment za različite vrijednosti parametra k. Prikaz prosječne apsolutne pogreške (MAE) za sustavu od 943 korisnika i 1682 proizvoda za različite vrijednosti parametra k, k={2,4,6,8,10,15,20,25} i fiksan parametar l=60.Najbolja kvaliteta postiže se za k=6 .
Veličina susjedstva, l, koje se promatra za određeni proizvod također ima utjecaj na kvalitetu preporuke. Najčešće slučaj je da je za blisko susjedstvo kvaliteta prema MAE niska, zatim proširenjem susjedstva MAE dostiže minimum, odnosno postiže se maksimalna kvaliteta za određeni broj susjeda. Nakon toga MAE postepeno raste što je prikazano na Slici
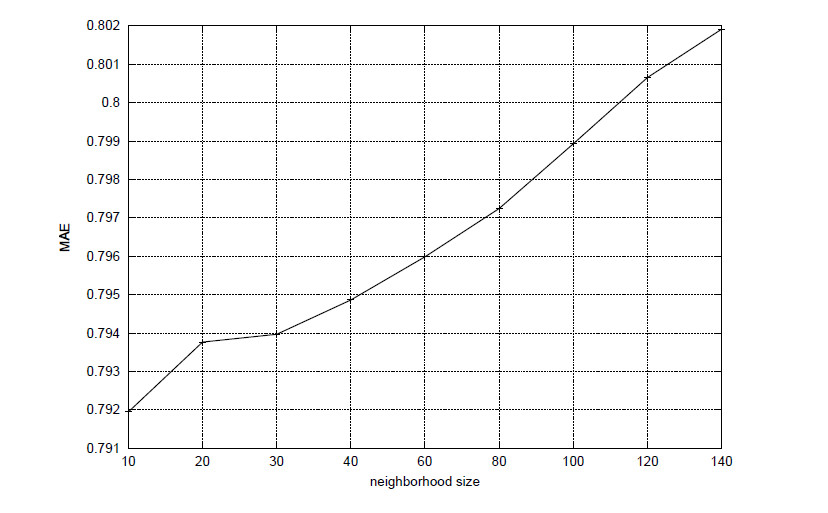
Slika 5: Eksperiment za različite vrijednosti parametra l. Prikaz prosječne apsolutne pogreške (MAE) za sustav od 943 korisnika i 1682 proizvoda za različite vrijednosti parametra l, l=\lbrace 10,20,30,40,60,80,100,120,140\rbrace i fiksan parametar k=6. Najbolja kvaliteta postiže se za l=10 .
Nedostatak CF algoritama baziranih na SVD dekompoziciji jest da se vrijeme računanja SVD dekompozicije povećava povećanjem broja proizvoda i korisnika u sustavu. Nadalje, dodavanjem novog korisnika u sustav ili pri promjeni početne matrice zbog novih vrijednosti iznova se mora off-line računati SVD dekompozicija sustava, što nije trivijalan postupak. U nastavku je opisan algoritam koji inkrementalno osvježava početni sustav nakon dodavanja novog korisnika.
Glavni problem prethodnog algoritma jest kako dodati korisnika u sustav bez ponovnog računanja modela cijelog sustava, odnosno bez ponovnog računanja SVD dekompozicije cijele matrice korisnosti. U matričnom jeziku, za dani novi vektor r_{new} i već poznatu matricu R potrebno je napraviti SVD dekompoziciju nove matrice \left[ \begin{array}{c} R \\ r_{new} \end{array} \right] koristeći već postojeću SVD dekompoziciju matrice R. U
Algoritam 2
| (1) |
Novi korisnik možda nije ocijenio sve proizvode te je odgovarajuća, nepopunjena mjesta vektora r_{new} prvo potrebno popuniti i to prosjecima pripadnih stupaca matrice R koji su ažurirani. Srednje vrijednosti stupaca dobivenih u 2. koraku Algoritma
(7)
\overline{s_{j}'} = \frac{m\cdot\overline{s_{j}} + \sum_{i=m+1, r_{ij}\neq 0}^{(m+p)}r_{ij}}{m+\sum_{i=m+1, r_{ij}\neq 0}^{m+p}1}
Još je potrebno elemente u svakom novom retku normalizirati s prosjekom tog retka. Za svaki i=(m+1),...(m+p) izračunati \overline{r_{i}'} kao u Algoritmu |
| (2) | Popunjen i normaliziran vektor r_{new} aproksimirati koristeći k-dimenzionalan prostor kako bi se dobio vektor r_{{new}_{k}}, tj. izračunati r_{{new}_{k}}=r_{new}V_{k}S_{k}^{-1}. |
| (3) | Aproksimaciju r_{{new}_{k}} se dodaje postojećoj SVD dekompoziciji matrice R (engl. folded-in) tako što se doda kao posljednji redak matrice U_{k}. Rezultat je modificirana matrica \hat{U_{k}}=\left[ \begin{array}{c} U_{k} \\ r_{{new}_{k}} \end{array} \right]\in\mathbb{R}^{(m+1)\times n} dok matrice V_{k} i S_{k} ostaju nepromijenjene. |
Nakon folding-in metode ponovno se izvršavaju koraci 5., 6. i 7. iz Algoritma
Postupak je moguće ponavljati više puta pri dodavanju jednog ili više korisnika odjednom. Nakon nekoliko iteracija, ovisno o količini i strukturi podataka koji su dodani, sustav će izgubiti na kvaliteti te će se morati ponovno off-line izračunati SVD dekompozicija za matricu R i nove podatke. Algoritam
Update metoda osvježavanja sustava pri dodavanju novog korisnika je složenija od folding-in metode, no krajnji rezultat ove metode je točna SVD dekompozicija novog sustava, do na pogrešku zaokruživanja, bez ponovnog računanja cijele SVD dekompozicije. Ovim postupkom se pri dodavanju novog korisnika u sustav odmah osvježava i prostor proizvoda u sustavu.
Pretpostavimo da u sustav želimo dodati novog korisnika kojeg možemo prikazati pomoću vektora r_{new}\in\mathbb{R}^{1\times n}. Matrica sustava je prethodno izračunata matrica R_{k} = U_{k}S_{k}V_{k}^{T} i poznajemo sve \overline{s_{j}} prosjeke stupaca matrice R. Zadaća metode update je osvježiti matrice U_{k}, S_{k}, V_{k} novim podatcima i prosjeke svih stupaca \overline{s_{j}} te dodati nove podatke u sustav. Prema
Algoritam 3
| (1) |
Nove podatke potrebno je dopuniti i normalizirati. Postupak je identičan koraku 1. iz Algoritma |
| (2) |
Izračunati projekciju r_{{new}_{k}} popunjenog i normaliziranog vektor r_{new}r_{{new}_{k}} = (I_{n} -V_{k}V_{k}^{T})r_{new}^{T} te SVD dekompoziciju matrice \hat{S_{k}} dane sa:
\hat{S_{k}}=\left[ \begin{array}{cc} S_{k} & 0 \\ r_{new}V_{k} & \Vert r_{{new}_{k}}\Vert \\ \end{array} \right]= U_{k}'S_{k}'V_{k}'^{T}
|
| (3) | Izračunati \hat{U_{k}}=\left[ \begin{array}{cc} U_{k} & 0 \\ 0 & 1 \\ \end{array} \right]U'_{k} |
| (4) | Izračunati \hat{V_{k}}=\left[ \begin{array}{cc} V_{k} & \frac{r_{{new}_{k}}}{\Vert r_{{new}_{k}}\Vert } \\ \end{array} \right]V'_{k} |
Nakon postupka update metode ponovno se izvršavaju koraci 5., 6. i 7. iz Algoritma
Prema
Algoritam 4
| (1) |
Pretpostavimo da u sustav dodajemo p novih korisnika te u tom slučaju matricu sustava treba proširiti matricom T\in \mathbb{R}^{p \times n} koja predstavlja matricu korisnosti za p novih korisnika i n proizvoda. Nove podatke potrebno je dopuniti i normalizirati kao što je opisano u 1. koraku Algoritma |
| (2) | Za matricu T_{norm} izračunati T_{k} = (I_{n} -V_{k}V_{k}^{T})T_{norm}^{T} i QR faktorizaciju14 te matrice T_{k}=Q_{T}S_{T}. |
| (3) |
Izračunati SVD dekompoziciju matrice
\hat{S_{k}}=\left[ \begin{array}{cc} S_{k} & 0 \\ T_{norm}V_{k} & S^{T}_{T} \\ \end{array} \right]= U_{k}'S_{k}'V_{k}'^{T}
|
| (4) | Izračunati \hat{U_{k}}=\left[ \begin{array}{cc} U_{k} & 0 \\ 0 & I_{p} \\ \end{array} \right]U'_{k} |
| (5) | Izračunati \hat{V_{k}}=\left[ \begin{array}{cc} V_{k} & Q_{T}\\ \end{array} \right]V'_{k} |
Također, kao kod Algoritma
Lako se može zaključiti da i ova metoda osvježavanja ima nedostatke, pogotovo ukoliko se odjednom u sustav dodaje mnogo korisnika. Prema
Metoda koja može smanjiti trošak osvježavanja sustava i zadržati kvalitetu preporuke je hibridna metoda folding-up koja je kombinacija metoda folding-in i update. Ideja metode je da u početku koristi metodu folding-in do unaprijed određenog udjela novih korisnika u sustavu. Nakon toga da se pokreće metoda update nad novim korisnicima kako bi se sustav vratio u ravnotežu i osvježio prostor proizvoda, taj proces se iterativno nastavlja kombiniranjem te dvije metode.
Osim teorijskih iskaza SVD algoritama za CF sustave, u ovome radu provedeni su eksperimenti za dane algoritme. Uz pomoć programskog paketa Matlab, implementirani je algoritam zasnovan na SVD dekompoziciji s redukcijom dimenzije te algoritmi za osvježavanje sustava folding-in i update metodom.
Prije same implementacije, potrebno je prikupiti i pripremiti podatke za testiranje. Testiranje algoritama provedeno je na manjem primjeru, odnosno na bazi od 11 korisnika i 11 proizvoda, a podatci za matricu korisnosti R, prikazanu Tablicom
| F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | F10 | F11 | |
| K1 | 3 | 0 | 5 | 0 | 3 | 4 | 0 | 0 | 0 | 0 | 0 |
| K2 | 0 | 3 | 5 | 3 | 0 | 4 | 0 | 3 | 0 | 0 | 3 |
| K3 | 4 | 0 | 5 | 3 | 3 | 4 | 4 | 0 | 4 | 0 | 0 |
| K4 | 5 | 3 | 5 | 0 | 5 | 5 | 0 | 0 | 0 | 0 | 5 |
| K5 | 4 | 4 | 5 | 5 | 4 | 5 | 0 | 3 | 0 | 3 | 3 |
| K6 | 4 | 4 | 4 | 4 | 5 | 5 | 0 | 0 | 0 | 0 | 0 |
| K7 | 0 | 5 | 0 | 0 | 4 | 0 | 0 | 3 | 0 | 0 | 0 |
| K8 | 0 | 4 | 5 | 0 | 5 | 3 | 0 | 0 | 0 | 5 | 0 |
| K9 | 5 | 4 | 0 | 5 | 3 | 4 | 5 | 0 | 5 | 4 | 0 |
| K10 | 0 | 5 | 5 | 0 | 4 | 2 | 0 | 0 | 0 | 0 | 0 |
| K11 | 3 | 0 | 5 | 4 | 5 | 0 | 4 | 5 | 2 | 0 | 5 |
Filmovi navedeni u matrici su redom: The Martian(2015), The Illusionist(2006), Now You See Me(2013), The Intouchables(2011), Ice Age(2002), Ted(2012), The Man Who Knew Infinity(2015), The Choice(2016), The Secret Life Of Pets(2016), Me Before You(2016) i Race(2016).
Algoritam zasnovan na SVD dekompoziciji s redukcijom dimenzije implementiran je u programskom paketu Matlab prema Algoritmu 1.
U ovom poglavlju promatraju se rezultati implementiranog algoritma i njegova točnost. Prvo su navedeni osnovni rezultati algoritma neophodni za predikciju, zatim su dani primjeri predikcije za zadanog korisnika u_{i} i film p_{j} i svojstva predikcije za slične proizvode i korisnike te je na kraju algoritam testiran za različite parametre k i l kako bi se odredili najbolji.
Kako je navedeno u algoritmu, prvi korak kod generiranja preporuke zasnovane na SVD dekompoziciji s redukcijom dimenzije jest popunjavanje i normalizacija matrice korisnosti. Prije svega normalizirali smo početnu matricu sustava R i dobivena matrica R_{norma} dana je sa:
Prema algoritmu sljedeći korak je SVD dekompozicija matrice R_{norm} i redukciju dimenzije na prethodno zadanu dimenziju obzirom na parametar k. Koristeći SVD dekompoziciju i Teorem
i to je model testnog sustava.
-
- a)
-
Promatra li se sličnost proizvoda za svaki par proizvoda u danom sustavu možemo konstruirati matricu (sim_{jf}) \in \mathbb{R}^{n\times n} koju nazivamo matrica sličnosti proizvoda, a elementi matrice dobiju se iz formule (
5) za svaki j,f = 1,\ldots, n. Općenito, matrica sličnosti proizvoda simetrična je matrica s jedinicama na dijagonali. Iz takve matrice danog sustava uočavamo da su najsličniji proizvodi, odnosno filmovi, redom:sim_{3,7}= 0.8223 \text{ , } sim_{1,9}=0.7467, \text{ i } sim_{8,11}=0.7884,što možemo potvrditi promatrajući Tablicu2 iz koje se vidi da su baš filmovi F3 i F7, F1 i F9, F8 i F11 najsličniji. - b)
-
Nakon što se izračuna sličnost svih filmova, može se odrediti l-susjedstvo za svaki film. Točnije, za svaki pojedini film odabrati njemu l najsličnijih filmova iz matrice sličnosti i kažemo da oni tada čine l-susjedstvo tog filma. Primjerice, za fiksni k=4 dobije se da 3-susjedstvo filma F2 čine filmovi F5, F1 i F6 te se film F2 nalazi u 3-susjedstvu filmova F1 i F6. Navedeno se može potvrditi i pažljivijim promatranjem podataka iz Tablice
2 . - c)
-
Napokon je moguće izračunati predikciju za određenog korisnika u_{i} i filma p_{j}. U ovom slučaju promatramo korisnika K7 i film F1, The Martian(2015). Predikcija je izračunata koristeći parametre k=2 i l=2 prema formuli (
6) za rezultat daje prediction_{7,1}=4.0177. Točnije, algoritam predviđa da će korisnik K7 rangirati sa 4 film The Martian(2015). Ukoliko se susjedstvo poveća ili se parametar k poveća dobiva se nešto drugačiji rezultat, odnosno za k=3 rezultat je 3.5215, a za l=3 je 3.7676 što potvrđuje da preporuka uistinu ovisi o parametrima l i k.
Iz Primjera
Analiza parametra k:
Testiranje za parametar k provedeno je za k=2,\ldots,8 i fiksan l=3, a rezultat je prikazan na Slici
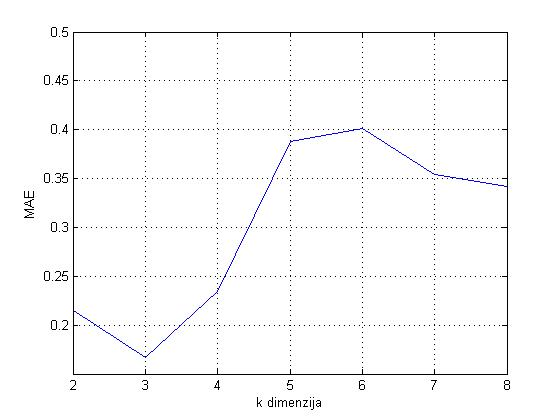
Slika 6: Za sustav dan Tablicom
Analiza parametra l: Testiranje za parametar l provedeno je za l=2,\ldots,8 i fiksan k=3, a rezultat je prikazan na Slici
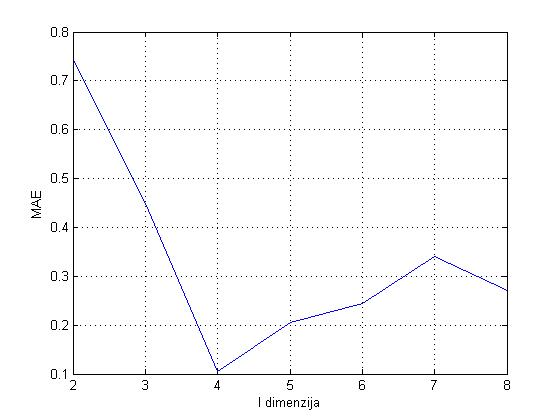
Slika 7: Za sustav dan Tablicom
Pri dodavanju svakog novog korisnika u sustav, dodaje se novi redak u matricu korisnosti, no ideja folding-in metode nije ponovno računanje SVD dekompozicije nego dodavanje korisnika u već reducirani sustav.
Odstupanje predikcije za novog korisnika rasti će dodavanjem sve većeg broja korisnika te bi se za sustav mogao promatrati i maksimalan broj korisnika koji se može dodati bez značajnog gubitka na kvaliteti. Kod većih sustava taj broj bi se mogao razmatrati, no u malim sustavima kao što je sustav iz primjera opadanje kvalitete je vidljivo već u samom startu. Osvježavanje sustava omogućuje dodavanje novog korisnika u sustav, a time rješava i cold start problem u CF sustavima.
Također, može se promotriti razlika u predikciji ukoliko se novi korisnik doda folding-in metodom ili se on dodaje u početni sustav ponovno računajući cijelu SVD dekompoziciju, što je prikazano u sljedećem primjeru.
U ovoj cjelini na testnom sustavu od 11 korisnika i 11 proizvoda ilustrirana je metoda update, implementirana kako je opisano u Algoritmima
Predikcija za korisnika K5 i film F5, Ice age(2002) iznosi 4.048. Predikcija za novog korisnika r_{new} i film F5 pomoću Folding-in metode iznosi 4.1867, a pomoću update metode iznosi 4.1301. Uočimo da je već na ovom malom primjeru vidljivo da je kvaliteta predikcije bolja kod metode update (MAE je manja).
Kod folding-in metode će dodavanjem sve većeg broja korisnika opadati kvaliteta predikcija, no u ovom slučaju kvaliteta se neće mijenjati bez obzira na broj novih korisnika. Primjerice, ako se dodaju tri korisnika kao korisnik K5, preporuka za K12 i film F5 iznosi 4.1697.
Kao prethodno, može se promotriti razliku u predikciji ukoliko se novi korisnik doda metodom update ili se doda u početni sustav ponovno računajući cijelu SVD dekompoziciju, što je prikazano u sljedećem primjeru.
U zadnjem primjeru promotrimo kakva će biti početna preporuka, ako se u sustav doda korisnik koji nije pogledao niti jedan film.
| [1] | Claudio Adrian Levinas, An Analysis of Memory Based Collaborative Filtering Recommender Systems with Improvement Proposals, Master of Science Thesis (2014.) |
| [2] | James W. Demmel, Applied Numerical Linear Algebra, University of California, Berkeley, Clifornia (1997.) |
| [3] | Manolis G. Vozalis, Konstantinos G. Margaritis, Applying SVD on Generalized Item-based Filtering, University of Macedonia, Thessaloniki, Greece (2006.) |
| [4] | Taghi M. Khoshgoftaar, Xiaoyuan Su, A Survey of Collaborative Filtering Techniques, Department of Computer Science and Engineering, Florida Atlantic University, USA (2009.) |
| [5] | Mirna Marković, Kolaborativno filtriranje, Odjel za matematiku, Sveučilište Josipa Jurja Strossmayera u Osijeku, diplomski rad (2016.) |
| [6] | Gene H. Golub, Charles F. Van Loan, Matrix computations (Johns Hopkins Studies in Mathematical Sciences), The Johns Hopkins University Press (1996.) |
| [7] | Jure Leskovec, Anand Rajaraman, Jeffrey D. Ullman, Mining of Massive Datasets, Second Edition (2014.) |
| [8] | Ninoslav Truhar, Numerička linearna algebra, Odjelu za matematiku, Sveučilišta J.J. Strossmayera, Osijek (2010.) |
| [9] | Alexander Paprotny, Michael Thess, Realtime Data Mining, Self-Learning Techniques for Recommendation Engines, Applied and Numerical Harmonic Analysis, Birkhäuser (2013.) |
| [10] | Charu C. Aggarwal, Recommender Systems:The Textbook, Springer (2016.) |
| [11] | Xiwei Wang, Jun Zhang, SVD-based Privacy Preserving Data Updating in Collaborative Filtering, Proceedings of the World Congress on Engineering, Vol I, London (2012.) |
| [12] | Yehuda Koren, The BellKor Solution to the Netflix Grand Prize (August 2009.) |
| [13] | Raymond J. Spiteri, Jane E. Tougas, Updating the Partial Singular Value Decomposition in Latent Semantic Indexing, NSERC Canada (2006.) |
| [14] | M.W. Berry, S.T. Dumais, G.W. O'Brein, Using Linear Algebra for Intelligent Information Retrieval, Computer Science Department, University of Tennessee, Knoxville (1994.) |
| [15] | Elaine Rich, User Modeling via Stereotypes (1979). |
| [16] | https://export-x.com/2015/12/11/how-many-products-does-amazon-sell-2015/ ExportX, 28.10.2016. |
| [17] |
http://hjp.znanje.hr, Hrvatski Jezični portal, 27.10.2016. |
Rezultati ankete:
https://docs.google.com/spreadsheets/d/1CL0j43vxyF6RVU0cp4pDvfJM GdME1fHtdm52QORUs94/edit?usp=sharing