|
Ozren Perše, Mila Strpić, Sanja Strpić |
Sažetak
U ovom preglednom radu prezentiramo dokaz iz S. Schneider, International Mathematical Forum 9 (2014) da se Riemannova i Cauchyjeva definicija integrabilnosti podudaraju. Također, diskutiramo odnos Riemannove i Darbouxove integrabilnosti.
1Uvod
Standardni udžbenici (vidi npr. [3], [4], [5]) i kolegiji matematičke analize uvode pojam određenog integrala ograničene funkcije f:[a,b]\to\mathbb{R} pomoću gornjih i donjih Darbouxovih suma pridruženih proizvoljnoj razdiobi \rho =\lbrace x_{k}\rbrace _{k=0}^{n} segmenta [a,b]. Razlog tome je što je ta definicija ipak na neki način operativnija od originalne Riemannove definicije pomoću integralnih (tj. Riemannovih) suma, za čiju definiciju je potrebno osim razdiobe \rho fiksirati i po jednu točku x_{k}^{*}\in [x_{k-1},x_{k}] iz svakog intervala pridruženog toj razdiobi. Riemannovu definiciju možemo ugrubo zapisati:
(1)
\begin{eqnarray} \int_{a}^{b}\!f(x)\,dx = \lim _{\Vert \rho\Vert \to 0} \Big( \sum_{k=1}^{n} f(x_{k}^{*})(x_{k}-x_{k-1}) \Big), \end{eqnarray}
ako taj limes postoji, pri čemu je s \Vert \rho\Vert označen dijametar razdiobe \rho. Jedna prednost ove definicije je što ne zahtijeva pretpostavku da je f ograničena funkcija. Naime, lagano se može pokazati da postojanje limesa u relaciji (1) povlači da je f:[a,b]\to\mathbb{R} ograničena.
Prirodno pitanje koje se postavlja je: Koliko možemo pojednostaviti definiciju (1) obzirom na izbor točaka x_{k}^{*}\in [x_{k-1},x_{k}]? Kao prirodni kandidati se javljaju rubovi intervala x_{k}^{*}=x_{k-1} ili x_{k}^{*}=x_{k}. Takvim razmišljanjem dolazimo do pojma Cauchyjevog integrala:
(2)
\begin{eqnarray} \lim _{\Vert \rho\Vert \to 0} \Big( \sum_{k=1}^{n} f(x_{k})(x_{k}-x_{k-1}) \Big), \end{eqnarray}
gdje smo uzeli x_{k}^{*}=x_{k}. Dakle, i pojam Cauchy-integrabilne funkcije je moguće definirati bez pretpostavke ograničenosti funkcije f. Međutim, za razliku od Riemannovog integrala, postojanje limesa u relaciji (2) ne povlači nužno ograničenost funkcije f (vidi Primjedbu 6).
Stoga dolazimo do formulacije glavnog problema ovog rada: Za ograničenu funkciju f:[a,b]\to\mathbb{R}, jesu li Riemannova i Cauchyjeva definicija integrala ekvivalentne? Budući da je jedan smjer očit, zapravo je potrebno dokazati da je svaka ograničena Cauchy-integrabilna funkcija ujedno i Riemann-integrabilna. Prvi dokaz te činjenice je dao D. C. Gillespie ([2]), koristeći teoriju mjere. U ovom radu prezentiramo nedavni dokaz S. Schneidera ([7]), koji koristi samo elementarne činjenice o Riemannovom integralu, odnosno taj dokaz je prilagođen slušačima standardnog kolegija realne analize funkcija jedne varijable.
U ovom radu, za ograničenu funkciju f:[a,b]\to\mathbb{R}, sa \sup(f, [a,b]) označavamo supremum funkcije f na segmentu [a,b], te s \inf(f, [a,b]) pripadni infimum.
2Riemannov i Darbouxov integral
Započinjemo sa standardnom definicijom određenog integrala, kojeg u ovom radu nazivamo Darbouxov integral.
Neka je f:[a,b]\to\mathbb{R} ograničena funkcija. Neka je
\rho =\lbrace x_{k}\rbrace _{k=0}^{n} =\lbrace a=x_{0} \lt x_{1} \lt \ldots \lt x_{n} =b \rbrace
razdioba segmenta [a,b]. Označimo s
\Vert \rho\Vert :=\max\lbrace x_{k}-x_{k-1}~:~ 1\leq k\leq n\rbrace
dijametar razdiobe \rho. Nadalje, označimo sa
\begin{array}{rcl} S(f,\rho) & := & \displaystyle{\sum_{k=1}^{n}(\sup(f, [x_{k-1},x_{k}]))\cdot (x_{k}-x_{k-1})}, \\ s(f,\rho) & := & \displaystyle{\sum_{k=1}^{n}(\inf(f, [x_{k-1},x_{k}]))\cdot (x_{k}-x_{k-1})} \end{array}
gornju i donju Darbouxovu sumu za funkciju f obzirom na razdiobu \rho, te s
\begin{array}{rcl} I^{*}(f) & := & \inf\lbrace S(f,\rho)~:~ \text{\(\rho\) je razdioba od \([a,b]\)}\rbrace , \\ I_{*}(f) & := & \sup\lbrace s(f,\rho)~:~ \text{\(\rho\) je razdioba od \([a,b]\)}\rbrace \end{array}
gornji i donji Darbouxov integral od f na [a,b].
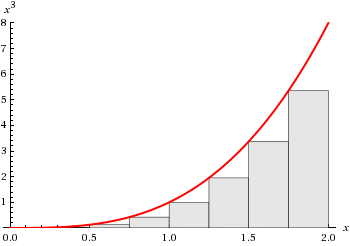
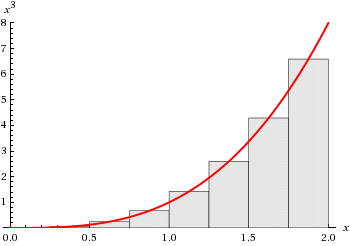
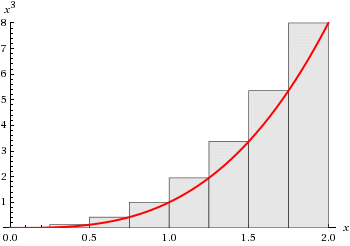
Donja Darbouxova suma, Riemannova suma i gornja Darbouxova suma
Definicija 1. Kažemo da je ograničena funkcija f:[a,b]\to\mathbb{R} Darboux-integrabilna ako je I^{*}(f) = I_{*} (f). U tom slučaju taj integral označavamo s \int_{a}^{b}\!f(x)\,dx.
Neka je sada f:[a,b]\to\mathbb{R} proizvoljna funkcija (ne nužno ograničena). Neka je \rho =\lbrace x_{k}\rbrace _{k=0}^{n} razdioba segmenta [a,b], te x_{k}^{*}\in [x_{k-1},x_{k}] proizvoljne točke, koje u ovom radu zovemo probne točke. Nadalje, označimo s
R(f,\rho,\lbrace x_{k}^{*}\rbrace ) \ := \ \sum_{k=1}^{n} f(x_{k}^{*})(x_{k}-x_{k-1})
Riemannovu (ili integralnu) sumu od f obzirom na razdiobu \rho=\lbrace x_{k}\rbrace _{k=0}^{n} od [a,b] i probne točke x_{k}^{*}\in [x_{k-1},x_{k}].
Definicija 2. Kažemo da je funkcija
f:[a,b]\to\mathbb{R} Riemann-integrabilna ako postoji
I\in\mathbb{R} takav da za svaki
\epsilon\gt 0 postoji
\delta\gt 0 takav da za sve razdiobe
\rho =\lbrace x_{k}\rbrace _{k=0}^{n} od
[a,b] s dijametrom
\Vert \rho\Vert \lt \delta i za sve izbore
\lbrace x_{k}^{*}\rbrace probnih točaka obzirom na
\rho, vrijedi
|R(f,\rho,\lbrace x_{k}^{*}\rbrace )-I|\lt \epsilon.
Sljedeći rezultat je vjerojatno dobro poznat čitatelju (vidi npr. [6], Poglavlje 10, gdje autori prezentiraju dokaz u slučaju funkcije dvije varijable):
Teorem 3. Vrijedi:
[(i)] Svaka Riemann-integrabilna funkcija f:[a,b]\to\mathbb{R} je nužno ograničena.
[(ii)] Ograničena funkcija
f:[a,b]\to\mathbb{R} je Darboux-integrabilna ako i samo ako je Riemann-integrabilna. Uz oznake kao u Definiciji
2 je
I= \int_{a}^{b}\!f(x)\,dx.
Dakle, Darbouxova integrabilnost i Riemannova integrabilnost su u suštini ekvivalentne.
3Riemannov i Cauchyjev integral
Pojam Cauchyjeve integrabilnosti dobivamo određenim pojednostavljenjem Riemannove integrabilnosti.
Neka je f:[a,b]\to\mathbb{R} proizvoljna funkcija (ne nužno ograničena). Neka je \rho =\lbrace x_{k}\rbrace _{k=0}^{n} razdioba segmenta [a,b]. Označimo s C(f,\rho) Riemannovu sumu koja za probne točke u svakom podintervalu uzima desne rubove x_{k}^{*}=x_{k}. Dakle,
C(f,\rho) \ := \ \sum_{k=1}^{n} f(x_{k})(x_{k}-x_{k-1}).
Modifikacijom Definicije 2 dobivamo:
Definicija 4. Kažemo da je funkcija
f:[a,b]\to\mathbb{R} Cauchy-integrabilna ako postoji
L\in\mathbb{R} takav da za svaki
\epsilon\gt 0 postoji
\delta\gt 0 takav da za sve razdiobe
\rho =\lbrace x_{k}\rbrace _{k=0}^{n} od
[a,b] s dijametrom
\Vert \rho\Vert \lt \delta, vrijedi
|C(f,\rho)-L|\lt \epsilon.
Očito je svaka Riemann-integrabilna funkcija ujedno i Cauchy-integrabilna. Cilj ovog rada je dokazati da uz pretpostavku da je f ograničena, vrijedi i obrat te tvrdnje. Ključnu ulogu u dokazu te činjenice ima sljedeća tehnička lema:
Lemma 7. Ako je
f:[a,b]\to\mathbb{R} ograničena, tada za svaki
\epsilon\gt 0 postoji razdioba
\rho od
[a,b] takva da je
S(f,\rho)-C(f,\rho)\lt \epsilon.
Dokaz. Fiksirajmo
B\gt 0 takav da je
\sup(f,[a,b])-\inf(f,[a,b])\leq B, i neka je
\epsilon\gt 0. Definirajmo
g:[a,b]\to\mathbb{R} s
g(x)=\sup(f,[x,b]). Tada je
g očito padajuća pa je i Riemann-integrabilna na
[a,b]. Označimo vrijednost tog integrala s
L, dakle
L=\int_{a}^{b}\!g(x)\,dx. Fiksirajmo
\delta_{1}\gt 0 takav da za svaku razdiobu
\rho ' od
[a,b] sa svojstvom
\Vert \rho '\Vert \lt \delta_{1} i za svaki izbor
x_{k}^{\ast} probnih točaka obzirom na
\rho', vrijedi
|R(g,\rho ',\lbrace x_{k}^{\ast}\rbrace )-L|\lt \epsilon. Neka je
\delta_{2}=\frac{\epsilon}{B}, i označimo
\delta=\min\lbrace \delta_{1},\delta_{2}\rbrace. Neka je
\rho ''=\lbrace x_{k}\rbrace _{k=0}^{n} razdioba od
[a,b] takva da je
\Vert \rho ''\Vert \lt \frac{\delta}{2}. Želimo pomoću
\rho '' dobiti željenu razdiobu
\rho. Neka je
\begin{array}{lll} C & = & \lbrace 1\leq k\leq n~:~ g(x_{k-1})=g(x_{k})\rbrace ; \\ D & = & \lbrace 1\leq k\leq n~:~ g(x_{k-1})\gt g(x_{k})\rbrace ; \\ D' & = & \lbrace k\in D\setminus\lbrace n\rbrace ~:~ k+1\not\in D\rbrace . \end{array}
Za svaki
k\in D' neka je
z_{k}=\inf\lbrace x\in [x_{k-1},x_{k}]~:~ g(x)=g(x_{k})\rbrace. Neka je
\begin{array}{lll} D_{0}' & = & \lbrace k\in D'~:~ g(z_{k})=g(x_{k})\rbrace ; \\ D_{1}' & = & \lbrace k\in D'~:~ g(z_{k})\gt g(x_{k})\rbrace . \end{array}
Za svaki
k\in D, izaberimo
y_{k}\in [x_{k-1},x_{k}) takav da je
|f(y_{k})-g(x_{k-1})|\lt \frac{\epsilon}{b-a}, pri čemu još dodatno vrijedi
y_{k}\lt z_{k} ako je
k\in D_{0}', te
y_{k}\leq z_{k} ako je
k\in D_{1}'. Nadalje, za svaki
k\in D' odaberimo dodatnu točku iz intervala
[x_{k-1},x_{k}] na sljedeći način. Ako je
k\in D_{0}', odaberimo
u_{k}\in (y_{k},z_{k}) tako da je
|u_{k}-z_{k}|\lt \frac{\epsilon}{B|D'|} i
|f(u_{k})-g(u_{k})|\lt \frac{\epsilon}{b-a}; ako je
k\in D_{1}', odaberimo
v_{k}\in (z_{k},x_{k}) tako da je
|v_{k}-z_{k}|\lt \frac{\epsilon}{B|D'|}. Definiramo sljedeće razdiobe:
\begin{array}{lll} \rho _{0} & = & \lbrace a,b\rbrace ; \\ \rho _{1} & = & \lbrace y_{k}~:~ k\in D\,\wedge\,k-1\not\in D\rbrace ; \\ \rho _{2} & = & \lbrace z_{k}~:~ k\in D_{0}'\rbrace \,\cup\,\lbrace v_{k}~:~ k\in D_{1}'\rbrace ; \\ \rho _{3} & = & \lbrace z_{k}~:~ k\in D_{1}'\,\wedge\,z_{k}\ne y_{k}\rbrace \,\cup\,\lbrace u_{k}~:~ k\in D_{0}'\rbrace \,\cup\,\lbrace y_{k}~:~ k,k-1\in D\rbrace ; \\ \rho & = & \rho _{0}\cup \rho _{1}\cup \rho _{2}\cup \rho _{3}. \end{array}
Pokazat ćemo da je
S(f,\rho)-C(f,\rho)\lt 6\epsilon.
Za svaki
q\in \rho, neka je
q'=q ako je
q=a, a inače neka je
q' najveći element od
\rho strogo manji od
q. Za
q\in \rho označimo
E_{q} \ := \ \big(\sup(f,[q',q])-f(q)\big)(q-q'),
pa je
S(f,\rho)-C(f,\rho) \ = \ \sum_{q\in \rho}E_{q} \ \leq \ \sum_{i=0}^{3}\left(\sum_{q\in \rho _{i}}E_{q}\right).
Ograničimo sada sume
\displaystyle{\sum_{q\in Q_{i}}E_{q}}, za sve
0 \leq i \leq 3.
Prvo primijetimo da ako je
g(x_{n-1})=g(x_{n}), tada je
\sup(f,[b',b])=f(b) pa je
E_{b}=0. S druge strane, ako je
g(x_{n-1})\gt g(x_{n}) tada je
n\in D pa je
b'\in [x_{n-1},b) odakle slijedi
E_{b}\lt \frac{B\delta}{2}. Budući da je
E_{a}=0, dobivamo
\sum_{q\in \rho _{0}}E_{q} \ \lt \ \frac{B\delta}{2} \ \lt \ \epsilon.
Nadalje, primijetimo da, ako je
q\in \rho _{1} tada je
q'=a ili
q'\in \rho _{2}. U oba slučaja je
\sup(f,[q',q])-f(q)\lt \frac{\epsilon}{b-a}, i stoga
\sum_{q\in \rho _{1}}E_{q} \ \lt \ \epsilon.
Ako je
q\in \rho _{2} tada je
q-q'\lt \frac{\epsilon}{B|D'|}, a budući da je
|\rho _{2}|\leq |D'|, to povlači
\sum_{q\in \rho _{2}}E_{q} \ \lt \ B|D'|\cdot\frac{\epsilon}{B|D'|} \ = \ \epsilon.
Konačno, neka je
q\in \rho _{3}. Ako je
q=z_{k}\ne y_{k} za neki
k\in D_{1}', tada je
g(q)=f(q) i
q'=y_{k} pa je
q-q'\lt \frac{\delta}{2}. Ako je
q=u_{k} za neki
k\in D_{0}', tada je
|f(q)-g(q)|\lt \frac{\epsilon}{b-a} i
q'=y_{k} pa je ponovo
q-q'\lt \frac{\delta}{2}. Ako je
q=y_{k} za
k,k-1\in D, tada
g(x_{k-1})-\frac{\epsilon}{b-a} \ \leq \ f(q) \ \leq \ g(q) \ \leq \ g(x_{k-1})
i
q'=y_{k-1} pa je
q-q'\lt \delta. Dakle, u svim slučajevima je
q-q'\lt \delta\leq\delta_{1} i
|f(q)-g(q)|\lt \frac{\epsilon}{b-a}. Neka je sada
\bar{\rho} proizvoljna razdioba od
[a,b] koja proširuje
\rho _{3}\cup\lbrace q'~:~ q\in \rho _{3}\rbrace, zadovoljava
\Vert \bar{\rho} \Vert \lt \delta_{1}, i nema točaka u intervalima
(q',q) za
q\in \rho _{3}. Tada je
\begin{array}{lllll} \displaystyle{\sum_{q\in \rho _{3}}E_{q}} & = & \displaystyle{\sum_{q\in \rho _{3}}\big(\sup(f,[q',q])-f(q)\big)(q-q')} & & \\ & \leq & \displaystyle{\sum_{q\in \rho _{3}}\big(g(q')-f(q)\big)(q-q')} & & \\ & \lt & \displaystyle{\epsilon+\sum_{q\in \rho _{3}}\big(g(q')-g(q)\big)(q-q')} & & \\ & \leq & \displaystyle{\epsilon+\sum_{q\in \bar{\rho} }\big(g(q')-g(q)\big)(q-q')} & & \\ & = & \displaystyle{\epsilon+\sum_{q\in \bar{\rho} } g(q')(q-q') - \sum_{q\in \bar{\rho} }g(q)(q-q')} & \lt & 3\epsilon. \end{array}
Uvažimo li sada gornje ograde za sume
\displaystyle{\sum_{q\in Q_{i}}E_{q}}, za sve
0 \leq i\leq 3, dobivamo:
S(f,\rho)-C(f,\rho) \ = \ \sum_{q\in \rho }E_{q} \ \lt \ 6\epsilon,
što dokazuje početnu tvrdnju, budući da je
\epsilon bio proizvoljan.
\ \blacksquare
Korolar 8. Ako je
f:[a,b]\to\mathbb{R} ograničena, tada za svaki
\epsilon\gt 0 postoji razdioba
\rho od
[a,b] takva da je
C(f,\rho)-s(f,\rho)\lt \epsilon.
Dokaz. Primijenimo Lemu
7 na funkciju
-f.
\ \blacksquare
Teorem 9. Neka je
f:[a,b]\to\mathbb{R} ograničena funkcija. Ako je
f Cauchy-integrabilna, tada je
f Riemann-integrabilna.
Dokaz. Neka je
L realan broj iz definicije Cauchy-integrabilnosti od
f na
[a,b]. Neka je
\epsilon\gt 0 proizvoljan, i fiksirajmo
\delta\gt 0 takav da za sve razdiobe
\rho od
[a,b] takve da je
\Vert \rho \Vert \lt \delta, vrijedi
|C(f,\rho)-L|\lt \epsilon. Neka je
\rho =\lbrace x_{k}\rbrace _{k=0}^{n} razdioba od
[a,b] takva da je
\Vert \rho \Vert \lt \delta. Koristeći Lemu
7 i Korolar
8, za svaki
1\leq k\leq n odaberimo razdiobe
\rho _{k}^{S} i
\rho _{k}^{s} od
[x_{k-1},x_{k}] takve da na
[x_{k-1},x_{k}] vrijedi
S(f,\rho _{k}^{S})-C(f,\rho _{k}^{S}) \ \lt \ \frac{\epsilon}{n}\quad\text{i}\quad C(f,\rho _{k}^{s})-s(f,\rho _{k}^{s}) \ \lt \ \frac{\epsilon}{n}.
Neka je
\rho^{S}=\cup_{k} \rho^{S}_{k} i
\rho^{s}=\cup_{k} \rho^{s}_{k}. Tada je
S(f,\rho^{S})-C(f,\rho^{S}) \ \lt \ \epsilon\quad\text{i}\quad C(f,\rho^{s})-s(f,\rho^{s}) \ \lt \ \epsilon.
Budući da je
\Vert \rho^{S} \Vert ,\Vert \rho^{s} \Vert \lt \delta, imamo
|C(f,\rho^{S})-L| \ \lt \ \epsilon\quad\text{i}\quad |C(f,\rho^{s})-L| \ \lt \ \epsilon.
Slijedi
S(f,\rho^{S})-s(f,\rho^{s}) \ \lt \ 4\epsilon.
Budući da je
\epsilon proizvoljan, odavde lagano slijedi da je
f Riemann-integrabilna na
[a,b].
\ \blacksquare
Bibliografija
|
[1] |
A.-L. Cauchy, Résumé des Leçons sur le Calcul Infinitesimal. (1823), p. 81.
|
|
[2] |
D.C. Gillespie. The Cauchy definition of a definite integral, Annals of Mathematics (2) 17 (1915), 61–63.
|
|
[3] |
B. Guljaš, Matematička analiza 1 i 2. skripta, https://web.math.pmf.unizg.hr/~guljas/skripte/MATANALuR.pdf
|
|
[4] |
S. Kurepa. Matematička analiza 1. Tehnička knjiga, Zagreb, 1989.
|
|
[5] |
S. Kurepa, Matematička analiza 2, Tehnička knjiga, Zagreb, 1990.
|
|
[6] |
P. Pandžić, J. Tambača, Integrali funkcija više varijabli, skripta, https://web.math.pmf.unizg.hr/nastava/difraf/predavanja_int.html
|
|
[7] |
S. Schneider. A note on Cauchy integrability. International Mathematical Forum 9 (2014), 1615–1620.
|





