
| LiveGraphics3D |  |  |
|
Sadržaj: 1. Primjer interaktivne 3D grafikeNa slici iznad prikazan je takozvani hiperbolički paraboloid, jedna od ploha drugog reda. Više o plohama drugog reda možete pročitati u on-line udžbeniku [IS], a o nastajanju hiperboličkog paraboloida na web stranici [SG]. Prikazana ploha je graf funkcije f(x, y) = x2 − y2 koja se obično navodi kao primjer preslikavanja koje ima "sedlastu točku" (stacionarnu točku koja nije točka lokalnog ekstrema). Ako čitate ispis ovog članka na papiru ili njegovu PDF verziju, nažalost ne možete vidjeti o čemu će u članku biti riječ. U on-line verziji članka ploha se počinje polagano rotirati kada pokazivač miša postavite iznad slike. Možete je sami zavrtjeti i u nekom drugom smjeru, brže ili sporije: kliknite mišem na sliku i pomaknite ga. Ako tipku miša otpustite dok je u pokretu, ploha će se nastaviti rotitati sve dok je pokazivač iznad slike. Osim toga, možete mijenjati uvećanje slike pritiskom na tipku SHIFT, klikom na sliku i pomicanjem miša gore ili dolje. U ovom članku opisat ćemo postupak kojim je napravljena interaktivna slika hiperboličkog paraboloida. Objasnit ćemo kako sami možete praviti slične prikaze trodimenzionalnih objekata i uključivati ih u vlastite web stranice. Objekti se generiraju u programskom sustavu Mathematica, a za prikaz se koristi Java applet LiveGraphics3D Martina Krausa [MK]. No, ne trebate biti stručnjak za računalnu algebru niti Java programer - pokušat ćemo vas uvjeriti da je generiranje takvih slika vrlo jednostavno! 2. Programski sustav MathematicaMathematica spada u sustave za računalnu algebru. Sličan komercijalni program "opće namjene" je Maple, a postoji i niz programa specijaliziranih za određene svrhe, npr. Matlab za matrične i druge numeričke proračune te slobodno dostupni sustav GAP za rad s konačnim grupama. Mathematica je u Hrvatskoj široko rasprostranjena jer Ministarstvo znanosti, obrazovanja i športa već niz godina plaća licenciju po kojoj se program može koristiti na hrvatskim sveučilištima. Ustrojen je Referalni centar za Mathematicu koji pruža podršku korisnicima, a nedavno je na Fakultetu elektrotehnike i računarstva održana konferencija o Mathematici. Programi ove vrste, osim računanja s približnim realnim brojevima, pružaju mogućnost egzaktnog i simboličkog računanja. Tako, naprimjer, u Mathematici postoji naredba Simplify s pomoću koje možemo pojednostavljivati algebarske izraze. Ako želimo skratiti algebarski razlomak
napisat ćemo:
Mathematica u izlaznoj liniji vraća ekvivalentan pojednostavljeni izraz. Pogledajmo kako se "nesređeni" razlomak interno prikazuje u Mathematici:
Ovaj algebarski razlomak, kao i bilo koji drugi objekt u Mathematici, reprezentiran je izrazom. Izraz se sastoji od glave (npr. Times, Power i Plus) i niza argumenata u uglatim zagradama odvojenih zarezima. Argumenti su i sami izrazi, ili su primitivni objekti poput brojeva ili varijable x. Ovo je jedina struktura podataka kojom se Mathematica koristi, a sva složenost leži u pravilima prema kojima se izrazi evaluiraju. Izraz s glavom Simplify zamijenit će se izrazom koji je ekvivalentan zadanom argumentu, ali je jednostavniji (izvrše se "skraćivanja razlomaka" i slične transformacije). Među najsloženijim pravilima su ona za evaluiranje izraza oblika Integrate[…]. Ta pravila izračunavaju neodređeni integral funkcije zadane argumentom. "Integrator" možete koristiti na webu čak i ako nemate instaliranu Mathematicu. Mathematica ima vrlo napredne mogućnosti vizualizacije funkcija i drugih matematičkih objekata. Naprimjer, hiperbolički paraboloid s početka članka dobiven je sljedećom naredbom:
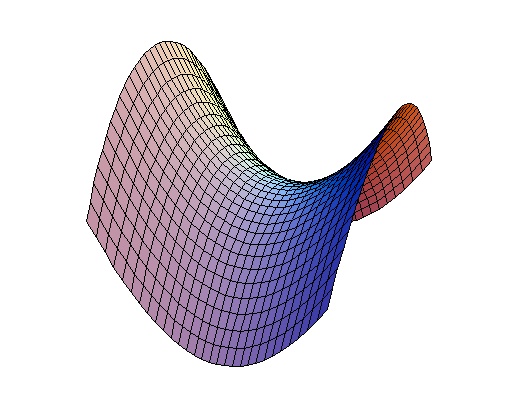
Slika koju je nacrtala Mathematica nije interaktivna poput prikaza na početku članka. Slika se lako prenosi iz Mathematice na web: desni klik, izbor Cell → Save Selection As i zatim odabir željenog formata. Alternativno, sliku možete "uhvatiti" svojim omiljenim grafičkim programom (tzv. screen capture). Snimljena slika može se uključiti na web stranicu kao što smo mi učinili u ovom članku. Međutim, interna reprezentacija nacrtanog hiperboličkog paraboloida bogatija je od same slike. U izlaznoj liniji dobili smo Graphics3D objekt koji se ne ispisuje. Možemo ga ispisati naredbama FullForm ili InputForm:
Prikazali smo samo prvi dio ovog izraza (Mathematica ispisuje 841 poligon). Izraz opisuje "kvadratiće" od kojih je sastavljena ploha. Vidimo da njihovi vrhovi imaju po tri koordinate, dakle riječ je zaista o opisu trodimenzionalnog objekta. Svođenje trodimenzionalnih objekata na obične slike usporedivo je s fotografiranjem kipova. Ugodnije je razgledavati kip sa svih strana nego gledati fotografije! 3. Java applet za prikaz Graphics3D objekataWeb je danas interaktivan medij. Interaktivnost se postiže programima koji se izvode na strani poslužitelja (servera), tj. računala na kojem je pohranjen sadržaj web stranice, ili programima koji se izvode na strani klijenta, tj. računala koje pristupa sadržaju web stranice preko preglednika (web browsera). Među najraširenijim rješenjima na strani klijenta su takozvani Java appleti, programi pisani u jeziku Java. Već u prvom broju math.e objavljen je članak Matrične transformacije ravnine [BZ] koji sadrži Java applete. Članci [SS], [ZC] i [HK] sadrže applete izrađene s pomoću programa GeoGebra i The Geometer's Sketchpad. Vjerujemo da većina čitatelja math.e na svojem računalu ima instaliran softver potreban za izvođenje Java appleta. Ako ne vidite sliku na vrhu ovog članka i interaktivne sadržaje u citiranim člancima, potrebno je instalirati besplatan Java plug-in. Martin Kraus s Tehničkog sveučilišta u Münchenu napravio je Java applet LiveGraphics3D [MK] za interaktivni prikaz Graphics3D objekata generiranih s pomoću Mathematice. Applet je slobodno dostupan na adresi http://www.vis.uni-stuttgart.de/~kraus/LiveGraphics3D i upotrijebili smo ga na početku ovog članka za prikaz hiperboličkog paraboloida. Ukratko ćemo opisati što treba napraviti da biste uključili prikaz trodimenzionalnog objekta na vlastitu web stranicu. Prvo treba generirati Graphics3D objekt. To je najjednostavnije napraviti u programu Mathematica, no moguće je konvertirati neke druge formate u Graphics3D objekte. Više o tome može pročitati u zadnjoj cjelini članka [RK] (naprimjer, moguće je prikazati objekte izrađene u programu Maple). Za ilustraciju poslužit će nam obična kocka:
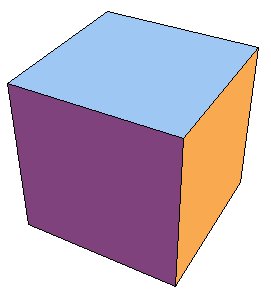
Ispišimo zatim sakriveni Graphics3D objekt. Koordinate ćemo zaokružiti na prvu decimalu da bi ispis bio kraći.
S pomoću funkcije Apply zamijenili smo glavu Graphics3D objekta s "live" da bi ga Mathematica ispisala. Umjesto toga možete ispisati vaš objekt s pomoću InputForm, ali onda koordinate neće biti kratke. U direktorij u kojem se nalazi vaša web stranica snimite datoteku live.jar i dodajte stranici sljedeći HTML kod: <applet archive="live.jar" code="Live.class" width="150" height="150"> <param name="INPUT" VALUE="Graphics3D[ ]"> </applet> Argumenti od Graphics3D ostavljeni su praznima. Na to mjesto potrebno je prenijeti sadržaj iz live[ ] koji smo dobili u Mathematici ("copy - paste" tehnikom).
<applet archive="live.jar" code="Live.class" width="150" height="150">
<param name="INPUT" VALUE="Graphics3D[
{Polygon[{{0.7, 0.7, 0.7}, {-0.7, 0.7, 0.7}, {-0.7, -0.7, 0.7}, {0.7, -0.7, 0.7}}],
Polygon[{{0.7, 0.7, 0.7}, {0.7, -0.7, 0.7}, {0.7, -0.7, -0.7}, {0.7, 0.7, -0.7}}],
Polygon[{{0.7, 0.7, 0.7}, {0.7, 0.7, -0.7}, {-0.7, 0.7, -0.7}, {-0.7, 0.7, 0.7}}],
Polygon[{{-0.7, 0.7, 0.7}, {-0.7, 0.7, -0.7}, {-0.7, -0.7, -0.7}, {-0.7, -0.7, 0.7}}],
Polygon[{{-0.7, -0.7, -0.7}, {-0.7, 0.7, -0.7}, {0.7, 0.7, -0.7}, {0.7, -0.7, -0.7}}],
Polygon[{{-0.7, -0.7, 0.7}, {-0.7, -0.7, -0.7}, {0.7, -0.7, -0.7}, {0.7, -0.7, 0.7}}]},
{Boxed -> False} ]">
</applet>
Minimalnu web stranicu s uključenim interaktivnim prikazom kocke pogledajte ovdje. LiveGraphics3D applet omogućuje zadavanje raznih parametara za inicijalni prikaz. Može se postići veća interaktivnost, prikaz objekata koji se izgrađuju "korak po korak", animacije u kojima korisnik zadaje parametre i još mnogo toga. Na web stranici [MK] dostupna je opsežna dokumentacija i daljnji primjeri. Ovdje možete testirati nekoliko osnovnih parametara. Pokušajte pritisnuti srednji ili desni gumb miša (ili tipku ALT i lijevi gumb) i pomicati ga vertikalno. To će brisati dijelove prikazanog objekta pa ćete, naprimjer, moći vidjeti unutrašnjost puža!
Appletom LiveGraphics3D koristi se i webMathematica, on-line inačica Mathematice. To je tipičan primjer interaktivnog sadržaja postignutog programima na strani poslužitelja. Korisnik u predviđena mjesta na web stranici upisuje svoj unos. Poslužitelj prosljeđuje te podatke programu Mathematica koji ih evaluira. Na temelju rezultata generira se posebna web stranica i isporučuje korisniku. Već spomenuti Integrator zasnovan je na webMathematici, a "vizualne" primjere koji se koriste LiveGraphics3D-om možete pogledati na stranicama Građevinskog fakulteta u Zagrebu. Na istom webMathematica poslužitelju nalaze se interaktivni primjeri iz sferne astronomije opisani u članku [HS]. Inače, LiveGraphics3D nije jedini slobodno dostupan Java applet za prikaz trodimenzionalnih objekata. Spomenut ćemo JavaView s još naprednijim mogućnostima prikaza, koji se također može koristiti uz Mathematicu ili uz Maple. Detaljan pregled appleta te namjene dan je na web stranici [GB]. 4. LiveGraphics3D na forumuInternetski forum (ili, kraće, samo forum) je mjesto na webu gdje posjetitelji mogu postavljati pitanja, davati odgovore, pisati komentare i slično. Ti tekstovi, takozvani postovi, povezani su u teme (eng. topics). Na mnogim forumima svatko može pisati i čitati što želi, no osoblje foruma to može više ili manje ograničiti. Trenutačno najraširenija vrsta foruma su phpBB forumi, među koje spada i forum časopisa math.e. Zasnovani su na programskom jeziku PHP i relacijskoj bazi podataka MySQL te predstavljaju još jedan primjer interaktivnosti postignute programima na strani poslužitelja. Više o spomenutim tehnologijama pročitajte u članku [NU] iz 6. broja math.e.
Za razliku od obične tekstualne komunikacije (npr.
korisničke grupe),
u tekstove na forumu moguće je dodavati slike, liste, osnovna
formatiranja teksta, "smajlije" Na forumima se za označavanje dodatnih elemenata upotrebljavaju takozvani BB-tagovi. Naprimjer, masno otisnuti tekst zapisuje se ovako: [b]masno otisnuti tekst[/b]. Forum časopisa math.e proširili smo BB-tagom [live]...[/live] koji poziva applet LiveGraphics3D. Tako i čitatelji koji nemaju iskustva s izradom web stranica i jezikom HTML mogu svoje Graphics3D objekte stavljati on-line. Osnovna sintaksa je:
Osim toga, BB-tag može appletu proslijediti parametre: [live=parametri]...[/live]. Parametre zadajemo u formatu ime:vrijednost i odvajamo ih znakom točka-zarez. Na forumu je omogućeno korištenje sljedećih parametara: WIDTH, HEIGHT, BGCOLOR, BACKGROUND, CYLINDRICAL_BACKGROUND, INITIAL_ROTATION, MAGNIFICATION, MOUSE_DRAG_ACTION, POINT_EDGE_COLOR, PRELOAD_BACKGROUND, RIGHT_BACKGROUND, SPHERICAL_BACKGROUND, SPIN_X, SPIN_Y, STEREO_DISTANCE, STRIPPED_PRIMITIVES, VISIBLE_FACES. Njihovi opisi dostupni su u dokumentaciji appleta. Ako nisu zadane dimenzije (parametri WIDTH i HEIGHT), veličina appleta bit će 150×150 piksela. Primjere korištenja BB-taga [live] pogledajte na forumu. Pozivamo vas da tamo postavite svoje trodimenzionalne objekte! Ako administrirate vlastiti phpBB forum i željeli biste ga proširiti BB-tagom [live], pripremili smo za vas instalacijsku skriptu (applet treba posebno preuzeti s autorove stranice). Literatura
1. Primjer interaktivne 3D grafike | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 i slično. Nabrojeni
elementi su uobičajeni, a neki forumi korisnicima pružaju i znatno šire
mogućnosti. Naprimjer, na forumu
i slično. Nabrojeni
elementi su uobičajeni, a neki forumi korisnicima pružaju i znatno šire
mogućnosti. Naprimjer, na forumu