
Broj 6



















Anamari Nakić, Ivo Ugrina
Internet baza matematičkih pojmova


Sadržaj:
1. Uvod
2. Internet
3. Relacijske baze podataka
4. MySQL i e-Ghetaldus
5. HTML i CSS
6. PHP
7. Skriptiranje na strani poslužitelja
8. Sučelja e-Ghetaldus-a
9. Pretraživanje uz pomoć Jaro-Winkler mjere sličnosti
10. Prikaz matematičkih simbola i formula na Internetu
11. Zaključak
Bibliografija
1. Uvod
U ovom bismo vam članku željeli opisati bazu matematičkih definicija e-Ghetaldus koja se nalazi na adresi www.baza.iugrina.com. Ime je dobila prema velikom hrvatskom matematičaru Marinu Getaldiću koji je živio i radio u 16. stoljeću.
Baza je nastala kao reakcija na nedostatak matematičkih sadržaja na hrvatskom jeziku na Internetu. Neslužbeni jezik elektroničkog svijeta jest engleski, no čak i oni studenti matematike koji ga dobro razumiju, slabo poznaju terminologiju matematičkih znanosti. Stoga se u bazi osim definicije pojma može pronaći i njegov naziv na engleskom jeziku te informacije o literaturi u kojoj se može saznati više o njemu.
Članak opisuje konkretni postupak implementacije baze. Prilikom implementacije koristili smo informatička i matematička znanja o relacijskih bazama, MySQL-u, HTML-u i PHP-u.
e-Ghetaldus se može koristiti na razne načine, a mi se nadamo da će se matematičari njome služiti dugo i uspješno. Osim toga, nadamo se da će potaknuti sve naše kolege da objavljuju više matematičkih sadržaja na Internetu na hrvatskom jeziku. Hrvatski jezik ne govori puno ljudi na svijetu, i bez podcjenjivanja snage jezika kojeg svi razumiju - engleskog, smatramo da to ne bi trebao biti razlog da se stručna i znanstvena literatura ne piše i na našem jeziku. Kako izdavanje knjige nije nimalo jeftino, a mala matematička zajednica ne garantira velike naklade, upravo suprotno, objavljivanje radova na Internetu čini se odličnom alternativom za one koji svoje znanje žele podijeliti s drugima. Baza podataka matematičkih pojmova na Internetu svima je dostupna i nedvojbeno korisna, a možda će biti i dobar početak za projekt popularizacije matematičkih znanosti u Hrvatskoj.
2. Internet
U današnje vrijeme svi smo na neki način korisnici kompjuterske tehnologije. Računala i Internet koriste se gotovo svakodnevno u svim dijelovima razvijenog svijeta. Iako se ponekad čini da čovječanstvo sporo prihvaća novitete, u samo pedesetak godina računala su uspjela osvojiti svijet, a Internet povezati ga.
Nastanak Interneta, a i računala, kao i njihov razvoj prvih godina zasluga je tehnološki najrazvijenije zemlje našeg vremena: Sjedinjenih Američkih Država. Internet je prekoračio granice SAD-a već u ranim sedamdesetim, a 1992. on prelazi prag od milijun računala raštrkanih posvuda u svijetu. Osnovan je Internet Society koje ga proglašava općim dobrom čovječanstva. 1993. godine osnovan je World Wide Web i Internet je ušao u svaki segment ljudskog djelovanja. Pokretanjem projekta CARNet (Croatian Academic and Research Network) 1991. godine počelo je uvođenje Interneta u Hrvatsku.
Internet je danas dostupan gotovo svim hrvatskim studentima. Bez Interneta e-Ghetaldus ne bi mogao niti postojati. Prilikom traženja bilo kakvih informacija, većina nas kreće od Interneta, stoga je on savršen medij za implementaciju e-Ghetaldusa. Niska cijena mrežnog prostora omogućuje svakome da objavi što želi. Noviteti iz svake domene ljudske djelatnosti tako danas puno brže objavljuju na Internetu nego u tiskanim formatima. Stoga je Internet postao pravo mjesto za objavu i potragu za relevantnim informacijama.
3. Relacijske baze podataka
Danas je teško zamisliti poslovnu ili web aplikaciju koja ne koristi relacijsku bazu podataka. Široku upotrebu ovih baza omogućilo je lako povezivanje baza sa aplikacijama pisanim u drugim programskim jezicima. Bilo je pokušaja da se razviju i neki drugi principi pohrane podataka, međutim SQL i relacijske baze podataka pokazale su se toliko dobrima da jednostavno nije bilo prevelikog interesa za nove ideje u tom području.
Student
|
Predavac
|
Kolegij
|
Bodovi
|
Osnove relacijskih baza podataka mogu se povezati s IBM-om te šezdesetim i sedamdesetim godinama prošlog stoljeća, i njihovom željom za automatiziranjem osnovnih uredskih poslova. Tih su godina tvrtke postajale svjesne da je jako skupo zapošljavati ljude samo za određene specijalizirane poslove, kao što su primjerice spremanje i indeksiranje datoteka. Radi uštede, odlučili su uložiti novac u istraživanja o jeftinijim i efikasnijim mehaničkim rješenjima. U tom je periodu provedeno mnogo istraživanja vezanih uz hijerarhijski, mrežni i relacijski model baza podataka.
Relacijski model baza podataka zasnovan je na matematičkom pojmu relacije.
Definicija.
| Neka je |
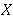
| skup, a |
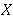
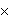
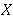
| Kartezijev produkt. Svaki podskup |
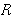
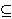
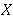
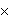
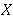
| tog produkta naziva se relacija na skupu |
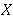
| . |
I podaci i veze među podacima prikazuju se "pravokutnim" tablicama. 1970. godine IBM-ov istraživač Ted Codd objavio je prvi članak o relacijskim bazama podataka. Članak je otvorio put za uporabu relacijske algebre koja je omogućila nestručnim korisnicima spremanje i traženje velikih količina podataka. Codd je predvidio sistem gdje korisnik može pristupati podacima s naredbama koje sliče engleskom jeziku, a informacije bi bile spremljene u tablice. Zbog tehničke prirode članka, i oslonca u matematici, važnost mu nije odmah uočena. Činilo se da takva složena teorija ne bi mogla imati široku primjenu. Međutim, doveo je do osnivanja IBM-ove istraživačke grupe zvane System R. Tokom vremena projekt System R razvio se u SQL/DS koji je kasnije postao DB2. Relacijski jezik koji je stvorila System R grupe, SQL (Structured Query Language) kasnije je postao industrijski standard za relacijske baze podataka i sada je ISO standard.
Nakon završetka rada na teoretskom dijelu SQL-a, stručnjaci iz IBM-a odlučili su objaviti svoj rad. Urednik tehničkog časopisa kojeg su odabrali za objavljivanje zahtijevao je da se u članku objavi i sintaksa za taj računalni jezik. Tako je u članku detaljno objašnjeno kako naredbe međusobno interaktiraju, što se može napraviti sa naredbama, koje su njihove forme, itd. Zbog objavljivanja sintakse druge su je kompanije mogle upotrijebiti za stvaranje sustava kompatibilnih sa IBM-ovim sustavom (i to su i učinile prije IBM-a). Prvi sustav za upravljanje bazom podataka napravljen po SQL standardu pojavio se početkom 1980-tih od kompanije Oracle, a kasnije SQL/DS od IBM-a.
S vremenom, baze podataka su se razvile od veličine 8Mb podataka koje je imao 'System R' do terabajta (1Tb = 10^12byte) podataka. Sve je više tvrtki postajalo svjesno prednosti korištenja SQL baza podataka i broj korisnika se povećavao. Kao što smo rekli, gotovo da i nema poslovne aplikacije koja ne koristi relacijske baze podataka. Pri izradi aplikacija programeri rade jednostavna sučelja preko kojih korisnici jednostavnim unošenjem podataka u polja (eng. textbox) i klikanjem na gumbiće unose podatke u bazu ne znajući kako baza funkcionira. Koliko će pohrana i dohvaćanje podataka biti optimalna ovisi o znanju i vještini programera te proizvođaču SQL-softvera.
MySQL je vrlo brz, efikasan, relacijski sustav za upravljanje bazom podataka (RDBMS) koji, kao što i ime kaže, koristi SQL. MySQL server kontrolira pristup podacima i omogućuje da više korisnika radi sa sustavom istovremeno, pruža brz pristup podacima i brine se da samo ovlašteni korisnici mogu pristupati podacima. MySQL je dostupan od 1996. godine, ali ima razvojnu povijest još od 1979. godine.
Primjer.
>> SELECT * FROM Student
Rezultat upita je JMBAG, ime i godina studija svih studenata.
Primjer.
>> SELECT PREZIME FROM Predavac WHERE SOBA = 211
Kao rezultat ovog upita dobit ćemo prezimena svih predavača koji imaju ured u sobi 211.
4. MySQL i e-Ghetaldus
Prije nego što implementiramo bazu podataka za projekt e-Ghetaldus potrebno je vidjeti koji su nam sve podaci potrebni. Želja nam je da baza sadrži definicije matematičkih pojmova i njihov engleski naziv pa će nam biti potrebni podaci: pojam, definicija i engleski naziv. Poželjna informacija korisnicima je i izvor te definicije.
- Pojam i engleski naziv
Logično je pretpostaviti da će broj slova u pojmu biti manji od 200, te da će većina pojmova imati između 5 i 30 slova. Tip podataka koji nam se zbog toga nameće jest VARCHAR (polje znakova varijabilne dužine). Iako je pristupanje podacima tipa VARCHAR sporije nego podacima tipa CHAR, zbog pretpostavke da će baza biti manja od 10 000 pojmova te zbog želje da uštedimo memoriju koristit ćemo tip VARCHAR. Iz istih razloga korist ćemo VARCHAR i za engleski naziv. U oba ćemo slučaja VARCHAR ograničiti na 200 znakova (VARCHAR(200)). - HTML oblik pojma
Osim samog pojma potrebno je sačuvati i HTML oblik pojma, odnosno kako ce se pojam prikazivati na stranicama. Primjerice, pojam neprekidna funkcija u Rn imati će HTML oblik neprekidna funkcija u R<sup>n</sup> što je neprimjeren oblik za pretraživanje, a opet potreban za identifikaciju pojma. Tip podataka koji ćemo koristiti je neograničeni VARCHAR. -
Definicija i izvor definicije
Kod definicija je puno teže procijeniti kolike će biti duljine pa ćemo koristiti tip podataka TEXT (može čuvati do 65.525 znakova). Za izvor ćemo koristiti ograničeni VARCHAR (VARCHAR(200)).
Sada je potrebno vidjeti što bi administratoru trebalo za uspješno vođenje takve baze. Bilo bi dobro kada bi se pamtio datum unošenja ili promjene definicije, svi pojmovi koji su traženi, a nema ih u bazi, koliko su puta traženi i na kojem jeziku.
- Datum promjene ili unosa
Za spremanje datuma promjene ili unosa koristit ćemo tip podataka DATE. DATE označava da će se datum pamtiti kao GGGG-MM-DD gdje G godina, M mjesec i D dan (na primjer 2005-10-02 je 2. listopada 2005.) - Traženi pojmovi, koliko su puta traženi i na kojem
jeziku
Koristiti ćemo VARCHAR za tražene pojmove iz već objašnjenih razloga, te UNSIGNED INT (prirodni brojevi) za broj puta koji su traženi te na kojem jeziku (0 za hrvatski jezik, 1 za engleski).
| Id2 | Pojam | HTML oblik | Definicija | Engleski naziv | Izvor |
| 1 | Ortogonalna matrica | Ortogonalna matrica | Definicija 1 | Orthogonal matrix | Izvor 1 |
| 2 | Ortogonalna matrica | Ortogonalna matrica | Definicija 2 | Orthogonal matrix | Izvor 2 |
| 3 | Dualni prostor | Dualni prostor | Definicija | Dual space | Izvor 3 |
| 4 | Linearni funkcional | Linearni funkcional | Definicija | Linear functional | Izvor 4 |
Ako sada odvojimo engleski naziv i stavimo ga u novu tablicu
eG_pojam zajedno s odgovarajućim pojmom, riješili smo
problem multipliciranja engleskog naziva i HTML oblika defincije,
ali i zauzeli više
memorije s obzirom da je pojam tipa VARCHAR. Možemo također odvojiti
i Izvor (ključ je Id4).
eG_definicija
|
eG_izvor
|
eG_pojam
| Pojam | HTML oblik | Engleski naziv |
| Ortogonalna matrica | Ortogonalna matrica | Orthogonal matrix |
| Dualni prostor | Dualni prostor | Dual space |
| Linearni funkcional | Linearni funkcional | Linear functional |
Radi jednostavnijeg zapisa i lakšeg pretraživanja, u tablici eG_definicija i
eG_pojam stavit ćemo stupac s prirodnim brojevima koji će
reprezentirati pojam. Za pamćenje datuma
promjene ili unosa definicije biti će nam potreban stupac tipa
DATE u tablici eG_definicija.
| Id2 | Id | Datum promjene | Definicija | Id4 |
| 1 | 1 | Datum1 | Definicija 1 | 1 |
| 2 | 1 | Datum2 | Definicija 2 | 2 |
| 3 | 2 | Datum3 | Definicija | 3 |
| 4 | 3 | Datum4 | Definicija | 4 |
| Id | Pojam | HTML oblik | Engleski naziv |
| 1 | Ortogonalna matrica | Ortogonalna matrica | Orthogonal matrix |
| 2 | Dualni prostor | Dualni prostor | Dual space |
| 3 | Linearni funkcional | Linearni funkcional | Linear functional |
Sada svaki pojam ima jedinstveni broj koji ga reprezentira (Id) te se svakoj definiciji može pristupiti pomoću tog broja. Izbjegli smo ponavljanje podataka te time i smanjili potrebnu memoriju. Ključ za tablicu eG_pojam je Id, a za tablicu eG_defincija Id2. Razdvojimo još HTML oblik na HTML hrvatski i HTML engleski.
| Id | Pojam | HTML hrvatski | HTML engleski | Engleski naziv |
| 1 | Ortogonalna matrica | Ortogonalna matrica | Orthogonal matrix | Orthogonal matrix |
| 2 | Dualni prostor | Dualni prostor | Dual space | Dual space |
| 3 | Linearni funkcional | Linearni funkcional | Linear functional | Linear functional |
Potrebno je još generirati tablicu eG_trazeni s pojmovima
koji su traženi, a nisu u bazi. To možemo na sljedeći
način (ključ je Id3):
| Pojam | Podrucje pretrage | Koliko | Id3 |
| Integral | 0 | 7 | 1 |
| Mjera | 0 | 14 | 2 |
| Perpendicular | 1 | 1 | 3 |
Upravo opisani postupak naziva se normalizacija (za podrobnije informacije pogledajte [6]) i kao rezultat dobivamo četiri tablice:
eG_pojam
|
eG_izvor
|
|||||||||||||||||||||||||||||||||||||||||
eG_definicija
|
eG_trazeni
|
5. HTML i CSS
Nakon implementacije same baze pomoću MySQL-a bilo je potrebno stvoriti web sučelje koje bi omogućilo korisnicima da putem Interneta koriste podatke koji se čuvaju u bazi, ali i administriranje same baze. U realizaciji ovog koraka koristili smo HTML, CSS i PHP.
HTML (Hyper Text Markup Language) je jezik dizajniran za izradu web stranica. Orijentiran je na strukturu web stranice. Dokumenti pisani u tekstu prikazuju se pomoću web preglednika kao što su Microsoft Internet Explorer, Netscape i Mozilla. HTML je jezik koji omogućuje uređivanje i dekoriranje web stranica, ali i prikaz različitih formi kao što su gumbi, potvrdni okviri (eng. checkbox) i slično.
Web-programeri sve više odvajaju sadržajni dio web-dokumenta od dijela koji se bavi izgledom same stranice. Odvajanje omogućuje lakši pristup sadržaju dokumenta, veću fleksibilnost i kontrolu u specifikaciji izgleda te jednostavniju strukturu dokumenta. Naredbe koje određuju izgled stranice odvajaju se u posebnu CSS-skriptu (Cascading Stylesheet Script). Kao i kod HTML-a, standard propisuje W3 konzorcij. CSS-om se koriste i autori i čitatelji web stranica kako bi definirali boje, fontove i druge prezentacijske karakteristike dokumenta.
CSS se u nekim početnim verzijama javlja početkom devedesetih godina prošlog stoljeća uz HTML. No, koncept koji je zaživio prihvaćen je 1994. godine. Nakon dvije godine rada W3 Konzorcij objavljuje CSS1 standard, no prošle su još tri godine prije nego su web preglednici implementirali CSS prema standardu. Aktualni standard je CSS2 i većina web preglednika ga ne podržava u potpunosti, a oni koji ga podržavaju sadrže brojne bugove. Ti su problemi u implementaciji potaknuli W3 Konzorcij da razmisli o vraćanju standarda na CSS1 pa je u pripremi CSS2.1 standard.
6. PHP
PHP je objektno-orijentiran skriptni jezik dizajniran specijalno za Web. Za razliku od HTML-a koji služi za generiranje statičkih web-dokumenata, PHP omogućava dinamičko generiranje sadržaja za web stranice. Unutar HTML dokumenta možemo staviti PHP kod koji će biti izvršen svaki put kada se dokumentu pristupi. PHP kod se interpretira na strani poslužitelja (server-side) i generira HTML, ili neku drugu vrstu dokumenta, kojoj korisnik pristupa.
PHP je dakle skriptni jezik. Njihova je osnovna karakteristika ta što se programi pisani u takvom jeziku ne kompajliraju već se interpretiraju. Kod kompajliranja se provjerava sintaksa programa i ako je sve u redu, stvara se izvršna datoteka. Tek kasnijim pokretanjem izvršne datoteke izvršavaju se naredbe napisane u programu, a ta je datoteka potpuno neovisna od one iz koje je nastala kompajliranjem . Kod skriptnih jezika nema tog međukoraka već se programi interpretiraju što dovodi do trenutnog izvršavanja naredbi. Stoga se programi pisani u skriptnim jezicima, iako nisu pogodni u svim situacijama, izvode jako brzo.
PHP je začet 1994. godine i u izvornom obliku rad je samo jednog čovjeka, Rasmusa Lerdorfa. Kasnije su se izradi pridružili i drugi stručnjaci te je sada plod rada više od 100 programera. U listopadu 2002. godine broj domena koje su ga koristile prešao je 9 milijuna, a sada se pretpostavlja da ga koristi oko 15 milijuna domena. Popularnost je stekao zbog jednostavne sintakse. PHP programi svojom strukturom podsjećaju na programe pisane u programskim jezicima kao što su Perl ili c. Taj skriptni jezik lako se uči, a web programeri ga vole jer nema stroga sintaktička pravila pa su moguće manipulacije s varijablama, poljima i tipovima podataka, nezamislive kod programskih jezika kao što su c++ ili Java (iako programeri koji koriste navedene jezike takve manipulacije smatraju gotovo svetogrđem).
7. Skriptiranje na strani poslužitelja
Osnovne operacije Web poslužitelja (eng. server) prikazane su na slici 1. Ovaj se sistem sastoji od dva objekta: Web preglednika (eng. browser) i Web poslužitelja. Web preglednik šalje zahtjev Web poslužitelju, a poslužitelj vraća rezultat zahtjeva. Ova arhitektura dobro odgovara prenošenju statičkih stranica (pisanih u HTML-u).
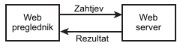
Slika 1. Osnovne operacije Web poslužitelja
Za rad s bazama podataka zahtjeva se malo kompleksnija struktura. Aplikacije s bazom podataka uglavnom se izvršavaju redoslijedom kao na slici 2. Mi ćemo prikazati sustav sa MySQL poslužitelja iako je proces većinom isti i za druge SQL poslužitelje.

Slika 2. Osnovne operacije Web poslužitelja s MySQL bazom podataka
- Korisnikov Web preglednik šalje HTTP zahtjev za određenom web stranicom. Nazovimo tu web stranicu primjer.php.
- Web poslužitelj prima zahtjev za datotekom primjer.php, uzima datoteku i prosljeđuje ju PHP mehanizmu.
- PHP mehanizam počinje procesuirati dokument (tzv. skriptu). Unutar skripte se nalazi naredba za spajanje s MySQL poslužiteljem i izvršavanjem upita prema bazi podataka. PHP mehanizam otvara vezu s MySQL poslužiteljem i šalje odgovarajući upit.
- MySQL poslužitelj prima upit i obrađuje ga, te vraća rezultat PHP mehanizmu.
- PHP mehanizam obrađuje ostatak skripte, koji će se uglavnom sastojati od oblikovanja rezultata upita u HTML. Obrađenu skriptu vraća kao HTML dokument Web poslužitelju.
- Web poslužitelj šalje HTML dokument do Web preglednika, gdje sada korisnik može vidjeti rezultat.
8. Sučelja e-Ghetaldus-a
Korisničkom sučelju baze e-Ghetaldus može pristupiti bilo tko. Osnovna funkcija koju bi e-Gethaldus trebao obavljati jest pronalaženje određene definicije s obzirom na korisnikov upit.

Slika 3. Primjer odgovora na korisnički upit
Za uspješno vođenje baze podataka potrebno je imati i administratorsko sučelje. Administrator mora biti u mogućnosti obavljati sljedeće poslove:
- unos podataka,
- brisanje podataka,
- mijenjanje podataka.
Osim toga, administrator je u mogućnosti vidjeti popis neuspjelih upita, tj. upita na koje baza nije pronašla odgovor. Tako može saznati više o području interesa korisnika i usmjeriti razvoj baze u tom pravcu.
Dodatak 2: Detalji implementacije sučelja i funkcija e-Ghetaldus-a
9. Pretraživanje uz pomoć Jaro-Winkler mjere sličnosti
Očekivati od korisnika da unese točan pojam čiju definiciju traži jest uistinu nerealno. Glavni razlog tomu nije lijenost korisnika već činjenica da se matematičari međusobno dobro razumiju i kada ne koriste pune nazive pojmova pa je za očekivati da će se tako ponašati i kada koriste bazu. Stoga je bilo potrebno da baza pronalazi točne odgovore i kada upit ne odgovara u potpunosti niti jednom pojmu koji je sadržan u njoj.
Funkcija za pretraživanje baze podataka e-Ghetaldus koristi Jaro-Winkler mjeru sličnosti
za uspoređivanje riječi.
Neka su zadane dvije riječi s = a1a2...aK i
t = b1b2...bL. Kažemo da je znak ai
u s pridružen t ako postoji bj=ai u t takav
da vrijedi i-H ≤ j ≤ i+H , gdje je H = min ( | s | ,| t | ) / 2. Neka su
s'=a'1a'2...a'K' znakovi u s pridruženi t
i neka su t'=b'1b'2...b'L' znakovi u t pridruženi s
(poredani u redoslijedu pojavljivanja u riječi s, odnosno t). Definirajmo sada transpoziciju
za s' i t' kao poziciju i takvu da vrijedi a'i≠b'i. Neka
je Ts',t' broj transpozijcija za s' i t' podijeljen sa dva. Jaro metrika za riječi
s i t dana je s
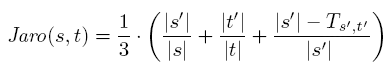 .
.
Rezultat Jaro mjere sličnosti je realan broj iz segmenta [0,1]. Veći broj predstavlja veću točnost, npr. 1 znači da su riječi jednake.
Primjer.
Izračunajmo sličnost riječi s = mtrica i t = matrica.
Ovdje je s = mtrica
= a1a2a3a4a5
a6 i t = matrica = b1b2b3b4b5
b6b7.
Vrijedi dakle,
| s | = 6, | t | = 7, H = min(6, 7) / 2 = 6 / 2 = 3. Pronađimo sada s'. Za
i = 1, tj. slovo m, mora postojati bj = m pri čemu je
1-3 ≤ j ≤ 1+3 . Takav j postoji i vrijedi j = 1.
Računamo dalje:
| i | s = mtrica | Uvijet | j | s' |
| 1 | a1 = m | 1-3 ≤ j ≤ 1+3 | 1 | b1 = m |
| 2 | a2 = t | 2-3 ≤ j ≤ 2+3 | 3 | b3 = t |
| 3 | a3 = r | 3-3 ≤ j ≤ 3+3 | 4 | b4 = r |
| 4 | a4 = i | 4-3 ≤ j ≤ 4+3 | 5 | b5 = i |
| 5 | a5 = c | 5-3 ≤ j ≤ 5+3 | 6 | b6 = c |
| 6 | a6 = a | 6-3 ≤ j ≤ 6+3 | 7 | b7 = a |
Dakle, s' = mtrica. Analogno tražimo t'. Ovdje je dakle t = matrica = a1a2a3a4a5 a6a7 i s = mtrica = b1b2b3b4b5 b6.
| i | t = matrica | Uvijet | j | t' |
| 1 | a1 = m | 1-3 ≤ j ≤ 1+3 | 1 | b1 = m |
| 2 | a2 = a | 2-3 ≤ j ≤ 2+3 | ne postoji | |
| 3 | a3 = t | 3-3 ≤ j ≤ 3+3 | 2 | b2 = t |
| 4 | a4 = r | 4-3 ≤ j ≤ 4+3 | 3 | b3 = r |
| 5 | a5 = i | 5-3 ≤ j ≤ 5+3 | 4 | b4 = i |
| 6 | a6 = c | 6-3 ≤ j ≤ 6+3 | 5 | b5 = c |
| 7 | a2 = a | 7-3 ≤ j ≤ 7+3 | 6 | b6 = a |
Jaro-Winkler je proširenje Jaro mjere sličnosti, rad William E. Winklera objavljen 1999. godine. Istraživanjem se pokazalo da prefiks ima veliku ulogu u sličnosti riječi pa je William E. Winkler pomoću Jaro mjere sličnosti definirao Jaro-Winkler mjeru sličnosti na sljedeći način,
gdje je prefixLength duljina zajedničkog prefixa između s i t te PREFIXSCALE konstantan realan broj kojim ćemo povećati ukupan rezulat. Očito je da će rezultati Jaro-Winkler i Jaro mjere sličnosti biti jednaki ako riječi s i t nemaju zajednički prefiks. Jaro-Winkler mjera sličnosti kao rezultat vraća realan broj, gdje veći broj predstavlja veću sličnost.
Kod pretraživanja pojmova, e-Ghetaldus će prikazati samo one pojmove iz baze čija je sličnost upitu veća ili jednaka 0.8. Ukoliko upit sadrži samo jednu riječ, a pojam u bazi više njih, upit će se usporediti sa svakom riječi te vratiti najveću vrijednost. Ukoliko upit sadrži više riječi, svaka od riječi upita usporediti će se sa svakom od riječi pojma te će se zapamtiti samo najveći rezultati za svaku od riječi upita. Od tih najboljih zatim će se odabrati minimalna vrijednost i to će se vratiti kao rezultat usporedbe.
Sljedeća tablica prikazuje neke rezultate Jaro-Winkler mjere sličnosti:
| Upit | Traženi pojam | Sličnost |
| neprekidnost | neprekidno preslikavanje | 0.9792 |
| mtrica | matrica | 0.9595 |
| jednakost | jednadžba | 0.9259 |
| jednakost | nejednakost | 0.8838 |
| presjek | prebrojiv | 0.8196 |
| neprekidnost | prekid | 0.75 |
| matrica | minimum | 0.5952 |
10. Prikaz matematičkih simbola i formula na Internetu
Matematičari često imaju problema s objavljanjem matematičkih sadržaja na Interentu jer HTML nema posebne naredbe za razne simbole koje koristi jezik matematike. Neki pišu tekstove u LaTeX-u i zatim ih objavljuju u pdf formatu. Neki se koriste raznim programima koji pdf dokumente pretvaraju u HTML dokumente, a formule koje nisu prikazive u HTML-u ugrađuju se u dokument kao slike. Mi smo se pri pisanju definicija u HTML-u koristili slikama matematičkih simbola u gif formatu koje smo zatim uz pomoć tablica slagali po potrebi u razne formule. Slike smo pronašli na web stranici us.metamath.org/symbols/symbols.html , a djelo su Normana Megilla. Na toj smo stranici pronašli i detaljne upute o izradi HTML dokumenata s matematičkim sadržajem.
11. Zaključak
U matematici postoje pojmovi kao što su skup, točka ili pravac koji se ne definiraju, ili za njih postoji definicija koja nije općeprihvaćena među matematičarima zbog svoje složenosti ili raznih drugih manjkavosti. Matematičari formalisti pronaći će među našim definicijama i 'definicije' koje to zapravo nisu. Ovim putem želimo napomenuti da smo i mi sami toga svjesni, no svejedno se i takvi pojmovi nalaze na našim stranicama, radi potpunosti, a i kako bismo onima koji uče i pretražuju Internet pomogli što više možemo.
Isto tako, trudili smo se izbjegavati teoreme, leme, propozicije i korolare, no prilikom definicije pojedinih pojmova bilo je nemoguće izbjeći formulaciju 'može se dokazati' jer smo time željeli istaknuti granicu između definicije i teorema. Postojanje nekih matematički objekata prvo se dokazuje, a tek zatim definira, stoga smo i to morali uzeti u obzir te istaknuti kako bi definicija bila razumljivija.
Razna svojstva pojedinih pojmova nismo nabrajali unutar definicije, ali se uz svaki pojam nalaze i informacije o knjizi/udžbeniku gdje smo pronašli definiciju, tako da svatko tko želi znati više, može ondje pronaći više informacija.
Sve definicije pronašli smo u knjigama, i trudili smo se minimalno improvizirati kako bismo ih što vjerodostojnije prenijeli. No, mnogi će od vas biti nezadovoljni stupnjem egzaktnosti koja se koristi pri definiranju pojedinih pojmova. Razlog što su neke definicije neformalne jest taj što smo ih pronašli u knjigama koje na slikovitiji i neformalniji način pokušavaju dočarati (budućem) matematičaru sam pojam. Kada smo unosili definicije krenuli smo od gradiva kolegija kao što su Matematička analiza 1 i 2, te Linearna algebra 1 i 2. Krenuli smo otpočetka. Literatura koja se koristi na tim kolegijima prilagođena je znanju početnika pa su tako i definicije jednostavnije. Nama to ne smeta i nismo takve definicije preskakali. Kako bismo zadovoljili sve, neki pojmovi na našim stranicama imaju i više definicija, počevši od onih neformalnih pa do onih egzaktnih prilagođenijih iskusnijim matematičarima.
Mlađim čitateljima Math-e, koje smo zainteresirali za naše stranice, a nisu upoznati s pojmovima koji se obrađuju na studiju matematike, preporučamo da počnu svoju pretragu pomoću Indexa pojmova. Možda će vam ova baza pomoći u shvaćanju što se sve uči na PMF-MO i potaknuti vas da svoje školovanje nastavite upravo ovdje.
Što se tiče daljnjeg razvoja baze, sadržajno, on će se kretati u području interesa korisnika. Već smo sada u mogućnosti vidjeti popis pojmova koje su korisnici tražili, a baza ne sadrži. Stoga će se budući sadržaji određivati prema zahtijevima korisnika.
U tehničkom dijelu, glavni cilj nam je poboljšanje algoritma pretrage. Osim po pojmovima, planiramo osposobiti bazu i za pretragu po tekstu definicija. Tada će korisnik biti u mogućnosti vidjeti gdje se sve u bazi pojavljuje pojam koji ga zanima. U bliskoj budućnosti, korisnici mogu očekivati implemetaciju pretraživanja po literaturi, što bi moglo pomoći onima koji uče za pojedini ispit.
Cilj nam je da e-Ghetaldus upotrebljava što veći broj korisnika, a da bi se to postiglo, potrebno je povećati broj definicija u bazi. Za sada nas je dvoje angažiranih na projektu, a zainteresirani smo za povećanje naše ekipe. Stoga, ako biste željeli bilo kako sudjelovati u ovom projektu, javite se na e-mail.
Bibliografija
[1] Paul DuBois: MySQL, New Riders Publishing, 2003.
[2] Preston Galla: Kako funkcionira Internet, Algoritam, Zagreb, 2004.
[3] Vitomir Grbavac: Informatika, kompjutori i primjena, Školska knjiga, Zagreb, 1988.
[4] Darko Grundler: Osobna računala: građa i primjena, KAP d.o.o., Zagreb, 1991.
[5] Sterling Hughes, Andrei Zmievski: PHP, Sams Publishing, 2002.
[6] Robert Manger: Baze podataka, Skripta, PMF-Matematički odjel, Zagreb, 2003.
[7] Željko Panian: Bogatstvo Interneta, Strijelac, Zagreb, 2001.
[8] Dragan Petric: Internet uzduž i poprijeko, Bug d.o.o., SysPrint d.o.o., Zagreb, 2002.
[9] Luke Welling, Laura Thomson: PHP and MySQL Web Development, Sams Publishing, 2004.
[10] William E. Winkler and Yves Thibaudeau: An Application of the Fellegi-Sunter Model of Record Linkage to the 1990 U.S. Decennial Census, Statistical Research Report Series RR91/09, U.S. Bureau of the Census, Washington, D.C., 1991.
[11] www.wikipedia.org
[12] www.carnet.hr/ela
1. Uvod
2. Internet
3. Relacijske baze podataka
4. MySQL i e-Ghetaldus
5. HTML i CSS
6. PHP
7. Skriptiranje na strani poslužitelja
8. Sučelja e-Ghetaldus-a
9. Pretraživanje uz pomoć Jaro-Winkler mjere sličnosti
10. Prikaz matematičkih simbola i formula na Internetu
11. Zaključak
Bibliografija