Hrvatski matematički elektronski časopis math.e

Broj 5 


 

Šime Šuljić

Mandelbrotov skup


3. Skup kompleksnih brojeva

Potreba proširenja skupa realnih brojeva. Znamo da postoje prirodni, cijeli, racionalni i iracionalni brojevi. Prirodni i cijeli brojevi zapravo se mogu prikazati kao razlomci pa ih smatramo racionalnima. Neki se korijeni ne mogu prikazati kao razlomci pa nisu racionalni. Na primjer, √2 nije racionalan broj. Racionalni i iracionalni brojevi čine skup svih realnih brojeva. Realni se brojevi mogu prikazati na brojevnom pravcu. Svakom realnom broju pridruži se jedna točka pravca i svakoj točki pravca pridružen je jedinstven broj. Slobodnih točaka nema, ali to ne znači da ne postoje brojevi osim realnih.

Imaginarna jedinica. U skupu realnih brojeva možemo kvadratni korijen računati samo iz nenegativnih brojeva. A koliko je, na primjer, √-1 ? Ne postoji takav realan broj koji bi kvadriran dao negativan broj! Stoga pretpostavimo da je riječ o nekom broju i, nazovimo ga imaginarnom jedinicom, za koji vrijedi:

i2 = -1.

Imaginarni brojevi. Koliko je onda √-4 ? √-4 = √4 ∙ √-1 = 2i. Tako možemo tvoriti beskonačno mnogo brojeva yi, gdje je y neki realni broj. Takve brojeve nazivamo imaginarnim brojevima.

Kompleksni brojevi. Ako postoji korijen iz negativnog broja, onda valjda postoji i korijen broja i? Postoji, to je broj (1 + i)/√2 . Uvjerite se da je rezultat kvadriranja tog broja imaginarna jedinica. Uočimo da je ovaj posljednji broj zapravo zbroj realnog broja i imaginarnog broja. Takve brojeve nazivamo kompleksnim brojevima i ima ih beskonačno mnogo. Obično ih označavamo slovom z. Općenito oni su oblika:

z = x + yi.

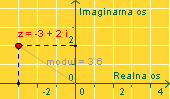
Klikom na sličicu otvara se aplet Kompleksna ravnina. Ako realne brojeve prikazujemo brojevnim pravcem, gdje ćemo smjestiti kompleksne brojeve? Kako se oni sastoje od dviju komponenti, realnog dijela x i imaginarnog dijela y, najbolje ih je pridružiti točkama ravnine. Tako dobivamo kompleksnu ravninu.
Napomena: Klikom na sličicu otvara se Java aplet, ali on se otvara nešto duže. To je samo pri prvom učitavanju, a kasnije se svi apleti otvaraju brzo. Ako ne vidite aplet, potrebno je instalirati Sun Javu.

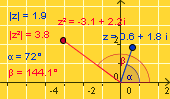
Kliknite na točku z u apletu i 'prošetajte' je ravninom. Promatrajte kako poprima različite vrijednosti kompleksnih brojeva. Njezinu udaljenost od ishodišta koordinatnog sustava zovemo modulom kompleksnog broja, oznaka je |z|. Kako se računa modul komleksnog broja ako je poznat njegov realni i imaginarni dio?

Zbrajanje kompleksnih brojeva. Kompleksne se brojeve zbraja po vrlo jednostavnom pravilu. Zbraja se realni dio jednog broja s realnim dijelom drugog broja. Isto vrijedi za imaginarne dijelove. Tako je:

(3 + 1i) + (-1 + 2i) = 2 + 3i.

Zanimljivo je uočiti geometrijsko svojstvo zbrajanja kompleksnih brojeva u kompleksnoj ravnini. Zbroj dvaju kompleksnih brojeva je broj pridružen točki koja je četvrti vrh paralelograma koji određuju točka pridružena prvom pribrojniku, ishodište koordinatnog sustava i točka pridružena drugom pribrojniku. Uvjerite se u to klikom na sličicu! Pomičite točke z1 i z2 i promatrajte zbroj z u apletu. 		Klikom na sličicu otvara se aplet

Klikom na sličicu otvara se aplet Kvadriranje kompleksnog broja. Uzmimo broj 1 + 2i. Kvadriramo ga kao binom: 12 + 2∙1∙2i + (2i)2. Rezultat je -3 + 4i. Otvorite aplet kvadriranje klikom na sličicu. U apletu možete pomicati broj z. Opet se uočava geometrijsko svojstvo kvadriranja broja. Modul kvadrata jednak je kvadratu modula broja z, a kut što ga zatvara spojnica točke pridružene broju z2 s pozitivnim dijelom realne osi dva je puta veći od odgovarajućeg kuta točke pridružene broju z.

 
◄ 2. Putovanje bez vodiča i itinerara

4. Iterativni postupak ►