
Hrvatski matematički elektronski časopis math.e

|
Hrvatski matematički elektronski časopis math.e |
| http://www.math.hr/~mathe/ |
Mandelbrotov skup
Šime Šuljić
"Vječnost nije dovoljna da ga se cijelog pregleda"
(James Gleick)

|
Susret s nepoznatim. "Naši daljinski senzori primili su signale koji se upravo prikazuju na ekranu pred nama. U središtu se pojavljuje slika. Što bi to moglo biti? Je li to neki kukac čudnovatog oblika? Možda je to, u stvari, neko tamno obojeno jezero, s mnogim planinskim potocima koji se ulijevaju u nj? ... Možda je to otok - i tada bismo mogli potražiti obližnji kontinent s kojim je on povezan." |
| Novi kontinent? "To možemo učiniti 'udaljavajući se', tj. smanjujući povećanje naših senzornih uređaja za linearni faktor od oko petnaest. I gle! Čitav svijet nam se pojavljuje pred očima. Naš nam "otok" sada izgleda tek kao točkica označena strelicom 1. Sve niti (potoci, putovi, mostovi?) koji polaze s prvotnog otoka završavaju, osim jedne koja se spaja s unutrašnjošću njegovog desnog udubljenja i koja ga povezuje s mnogo većim objektom koji vidimo na slici 2. Ovaj veći objekt očigledno je sličan otoku koji smo prije vidjeli - iako ne sasvim isti. Ako se usredotočimo na ono što izgleda da je obala tog objekta, vidimo izrasline - okruglaste, koje i same imaju slične izrasline na sebi. Svaka mala izraslina izgleda kao da je pričvršćena za veću na nekom uskom mjestu, stvarajući mnogo bradavica na bradavicama. Kako slika postaje jasnija, vidimo mirijade (grč. bezbroj) tankih vlakana koja izlaze iz strukture. Sama vlakna račvaju se na različitim mjestima i često divlje vrludaju. Na nekim točkama vlakana vidimo male račvaste čvorove, koje naši senzorski uređaji, sa sadašnjim povećanjem, ne mogu razdvojiti. Jasno je da objekt nije stvaran otok ni kontinent ni kakav krajolik. Možda, na kraju, vidimo nekog monstruoznog kukca, a prvo što smo vidjeli bio je jedan od njegovih potomaka, još pričvršćen za njega nekom vlaknastom pupčanom vrpcom." |

|

| Čudna bradavica. "Pokušajmo ispitati prirodu jedne od bradavica našeg stvorenja, prilagođavajući povećanje našeg senzorskog uređaja za linearni faktor od oko deset, mjesto označeno strelicom 3 na prethodnoj slici. Sama bradavica podsjeća na cijelo stvorenje - osim u samoj točki spajanja. Zapazimo da postoje različita mjesta na slici gdje se susreće pet vlakana. Postoji neka 'peterostrukost' u vezi s ovom bradavicom (kao što bi postojala izvjesna 'trostrukost' u slučaju bradavice u gornjem dijelu cijele slike)." |
| Dolina morskog konjica. "Kako ulazimo u otvor između dvaju najvećih područja na slici 2 na desnoj strani, otkrivamo bradavice koje karakteriziraju neparni brojevi, koji se svaki put uvećaju za dva. Zavirimo duboko unutar tog otvora, prilagođavajući povećanje za faktor od oko deset. Sada vidimo brojne druge bradavice i slična vrtložna gibanja. Na desnoj strani, možemo razabrati spiralne 'repove morskog konjica'." |
|

|
Koraljni greben. "Možda je, na kraju, ovo zaista neka egzotična obala - neki koraljni greben, ispunjen životom svakojake vrste. Ono što izgleda kao cvijet, razotkriva se pri daljem povećanju kao mnoštvo sitnih, ali nevjerojatno složenih struktura, od kojih svaka ima brojne vlaknaste i vrtložne spiralne repove. Ispitajmo jedan od njih." |
| Plodonosni susret spirala. "Na mnogim mjestima struktura je povezana samo tamo gdje se sastaju dvije spirale. Ispitajmo jedno od ovih mjesta, prilagodivši naše povećanje za odgovarajući faktor. I gle: vidite li čudan, ali sada poznat objekt u sredini?" |

|

|
Fascinantna sličnost. "Daljnje povećanje otkriva majušno 'dijete' - stvorenje skoro istovjetno čitavoj strukturi koju ispitujemo! Ako pogledamo bolje, vidjet ćemo da se vlakna koja izlaze iz nje malo razlikuju od onih koja izlaze iz glavne strukture, ali ona zavijaju i šire se do mnogo većih udaljenosti. Ipak, mala stvorenja jedva se razlikuju od svojih roditelja." |
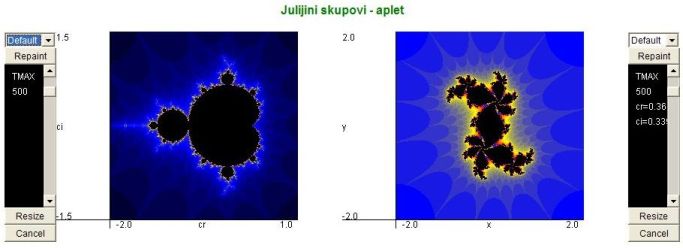
Mišem jednostavno označite područje na slici i pustite da se to područje poveća. Potrudite se da to područje bude što je moguće više kvadrat da ne dolazi do izobličenja. Želite li što detaljniju sliku, povećajte parametar TMAX na Repaint, a za povratak na početnu sliku kliknite na Resize.
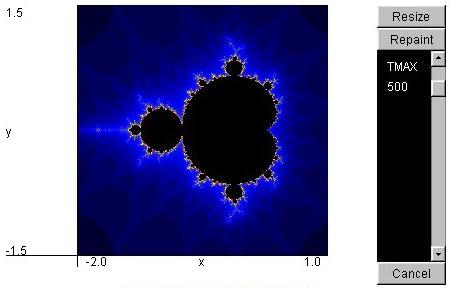
Autor apleta je profesor
Takashi Kanamaru.
Imaginarna jedinica. U skupu realnih brojeva možemo kvadratni korijen računati samo iz nenegativnih brojeva. A koliko je, na primjer, √-1 ? Ne postoji takav realan broj koji bi kvadriran dao negativan broj! Stoga pretpostavimo da je riječ o nekom broju i, nazovimo ga imaginarnom jedinicom, za koji vrijedi:
i2 = -1.
Imaginarni brojevi. Koliko je onda √-4 ? √-4 = √4 ∙ √-1 = 2i. Tako možemo tvoriti beskonačno mnogo brojeva yi, gdje je y neki realni broj. Takve brojeve nazivamo imaginarnim brojevima.
Kompleksni brojevi. Ako postoji korijen iz
negativnog broja, onda valjda postoji i korijen broja i?
Postoji, to je broj
z = x + yi.
|
Kompleksna ravnina. Ako realne brojeve prikazujemo
brojevnim pravcem, gdje ćemo smjestiti kompleksne brojeve?
Kako se oni sastoje od dviju komponenti, realnog dijela x i
imaginarnog dijela y, najbolje ih je
pridružiti točkama ravnine. Tako dobivamo
kompleksnu ravninu. |
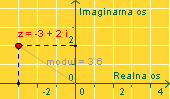
Kliknite na točku z u apletu i 'prošetajte' je ravninom. Promatrajte kako poprima različite vrijednosti kompleksnih brojeva. Njezinu udaljenost od ishodišta koordinatnog sustava zovemo modulom kompleksnog broja, oznaka je |z|. Kako se računa modul komleksnog broja ako je poznat njegov realni i imaginarni dio?
|
Zbrajanje kompleksnih brojeva.
Kompleksne se brojeve zbraja po vrlo jednostavnom pravilu.
Zbraja se realni dio jednog broja s realnim dijelom drugog broja.
Isto vrijedi za imaginarne dijelove.
Tako je:
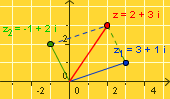
(3 + 1i) + (-1 + 2i) = 2 + 3i. Zanimljivo je uočiti geometrijsko svojstvo zbrajanja kompleksnih brojeva u kompleksnoj ravnini. Zbroj dvaju kompleksnih brojeva je broj pridružen točki koja je četvrti vrh paralelograma koji određuju točka pridružena prvom pribrojniku, ishodište koordinatnog sustava i točka pridružena drugom pribrojniku. Uvjerite se u to klikom na sličicu! Pomičite točke z1 i z2 i promatrajte zbroj z u apletu. |
|
|
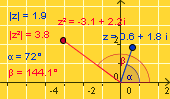
Kvadriranje kompleksnog broja. Uzmimo broj 1 + 2i. Kvadriramo ga kao binom: 12 + 2∙1∙2i + (2i)2. Rezultat je -3 + 4i. Otvorite aplet kvadriranje klikom na sličicu. U apletu možete pomicati broj z. Opet se uočava geometrijsko svojstvo kvadriranja broja. Modul kvadrata jednak je kvadratu modula broja z, a kut što ga zatvara spojnica točke pridružene broju z2 s pozitivnim dijelom realne osi dva je puta veći od odgovarajućeg kuta točke pridružene broju z. |
Pravilo. Uzmemo neki kompleksni broj c. Kvadriramo ga i dodamo sam početni broj c; ono što dobijemo, opet kvadriramo i dodamo početni broj c; ono što dobijemo, opet kvadriramo i dodamo početni broj c, itd. Takav niz iteracija možemo iskazati formulama:
z1 = z02+ c
z2 = z12+ c
z3 = z22+ c
…
zn+1 =
zn2 + c,
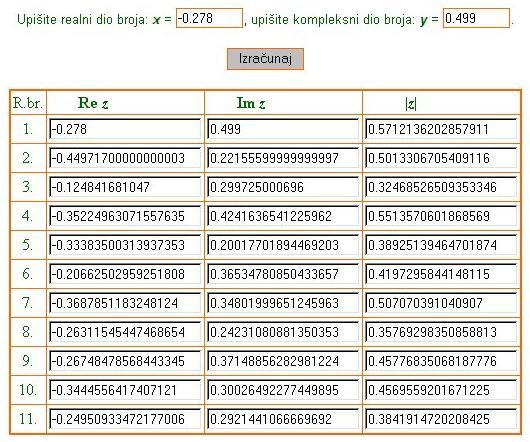
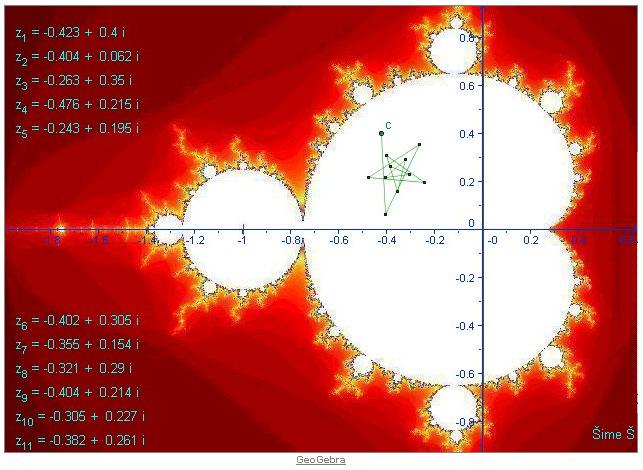

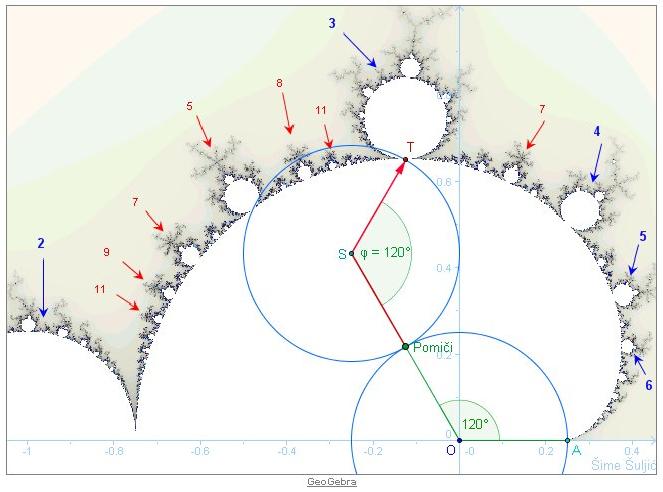
Glavno tijelo našeg objekta proučavanja je kardioida. Po definiciji, kardioida je krivulja koju opisuje točka kružnice koja se kotrlja bez klizanja po nepokretnoj kružnici istog polumjera, pri čemu se kružnice dodiruju izvana. Pogledajte aplet:


| Benoit Mandelbrot rođen je u Varšavi 1924. godine. Njegova je obitelj zbog straha od nacizma emigrirala 1936. godine u Pariz, gdje je na École Normale i École Polytechnique stekao matematičko obrazovanje. Poslije se zaposlio u IBM-ovom istraživačkom centru Thomas J. Watson. Baveći se fraktalnim oblicima skovao je naziv fraktal od pridjeva fractus, što bi značilo slomljen, razlomljen. Mandelbrot je postao svojevrsni guru nove znanstvene discipline teorije kaosa, a skup koji je otkrio postao je amblem te teorije. |

|
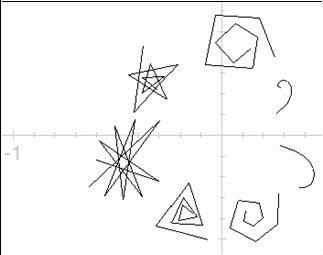
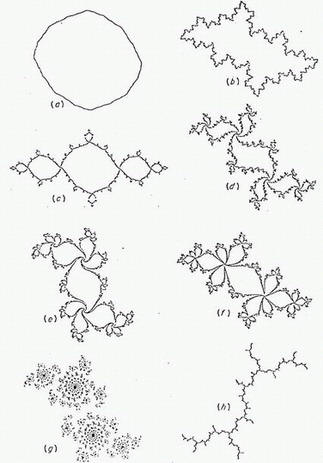
Kada je Mandelbrotu bilo dvadeset godina došao mu je u ruke već zaboravljeni rad "Mémoire sur l'iteration des fonctions rationelles", što ga je za vrijeme prvog svjetskog rata napisao francuski matematičar Gaston Julia. Julia je shvatio da se iterativnim postupcima u kompleksnoj ravnini mogu stvarati mnogi skupovi. U to doba bez računala, skromni crteži koje su on i Pierre Fatou napravili bili su zapravo više nego fascinantni.
z1 = z02+ c
z2 = z12+ c
z3 = z22+ c
…
zn+1 =
zn2 + c
|
|
|
|
|
J. Gleick: Kaos - rađanje nove znanosti, Izvori, Zagreb, 2000. |
Z. Sardar, I. Abrams: Kaos za početnike, Naklada Jesenski i Turk, Zagreb, 2001. |
Ivica Vuković: Mandelbrotov skup, Matematičko-fizički list, 94./95. br. 2. |
Sadržaji na Internetu. Toga ima toliko da pretraživač Google daje preko pola milijuna dokumenata s pojmom Mandelbrot. Ovdje je tek nekoliko linkova iz tog "kaosa":
Neki računalni programi. Svi su besplatni.