Hrvatski matematički elektronski časopis math.e

Broj 5 


Nagradni zadatci



Nagradni zadatci u petom broju povezani su s člancima Benfordov zakon i Mandelbrotov skup, pa preporučujemo da pogledate te članke prije rješavanja zadataka.

Rješenja zadataka pošaljite elektronskom poštom na našu e-mail adresu

mathe@math.hr.

Najbrže i najuspješnije rješavatelje nagradit ćemo knjigama u izdanju Hrvatskog matematičkog društva. Popis izdanja HMD-a možete pogledati na ovoj stranici. Uz rješenje (obrazloženo), napišite ime škole ili fakulteta koji pohađate, razred ili godinu studija, te adresu na koju želite da vam se pošalje nagrada. Također, možete napisati i koju biste knjigu s navedenog popisa željeli dobiti kao nagradu.


1. Niz Fibonaccijevih brojeva definiran je s

F1 = 1, F2 = 1, Fn+2 = Fn+1 + Fn.

Koja je "vjerojatnost" (tj. relativna frekvencija pojavljivanja) da je u Fibonaccijevom broju druga znamenka 4 puta veća od prve znamenke?
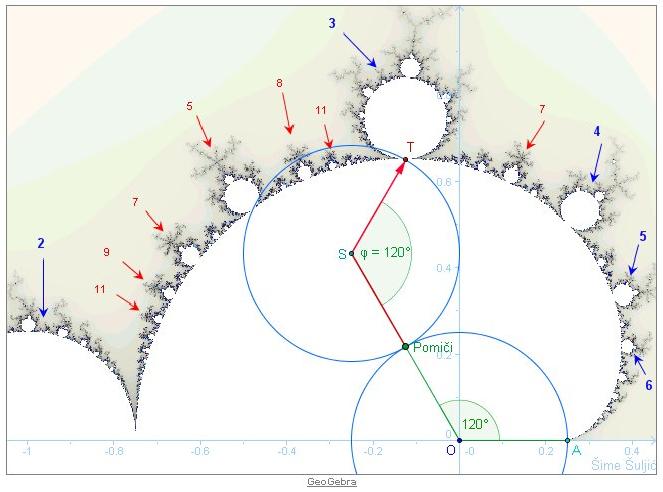
(Uputa: Rezultat je dekadski logaritam jednog racionalnog broja.
Priznat će se i rezultati dobiveni eksperimentalno, ukoliko budu obrazloženi i popraćeni korištenim programom.)


2. Neka je φ kut što ga zatvara polumjer ST sa spojnicom OS središta kružnica (vidi sliku). Kada se točka T nalazi u dodirnoj točki bradavice i glavnog tijela Mandelbrotovog skupa kut φ je u uskoj je vezi s periodom.

Pronađite pravilo (ili pravila) za određivanje kuta φ za pojedine bradavice. Posebno, odredite točnu vrijednost kuta φ za bradavice čiji su periodi na slici označeni strelicama.

(Savjet: Najprije odredite kutove za bradavice označene plavim strelicama - za njih je pravilo vrlo jednostavno. I naravno, koristite aplet iz članka.)




Rješenja zadataka i nagrađeni rješavatelji