
Broj 5











Bojan Radman
Benfordov zakon

Sadržaj:
UvodPovijest Benfordovog zakona
Primjeri Benfordovog zakona
Izvod Benfordovog zakona
Zaključak
Literatura
Uvod
Promatrajući neku stranicu telefonskog imenika, što mislite koja će se znamenka pojavljivati najčešće kao prva u telefonskim brojevima na toj stranici? Ograničimo se još na to da promatramo samo prvu značajnu znamenku u broju (tj., prvu znamenku različitu od nule). Vrlo vjerojatno očekujete da će se otprilike jednak broj puta na prvom mjestu pojaviti znamenke 1, 2, 3, 4, 5, 6, 7, 8, 9, tj. da je vjerojatnost pojavljivanja bilo koje od ovih 9 znamenaka na prvom mjestu jednaka i iznosi oko 0.111, tj. 11.1%. Međutim, to nije istina! Ako imate strpljenja prebrojiti te znamenke, otkrit ćete nešto pomalo iznenađujuće. Broj 1 pojavljuje se mnogo češće kao prva značajna znamenka od ostalih. Ovo je primijetio i Benford prije više od 60 godina. Svi znamo da se naš brojevni sustav koristi znamenkama od 0 do 9 i da je vjerojatnost slučajno odabrane prve značajne znamenke u broju 1/9 (ovdje opet izbacujemo nulu jer ona ne može biti prva značajna znamenka u broju). Ovo vrijedi za podatke generirane Random funkcijom ili neke lažne izmišljene podatke. Kod podataka koji se pojavljuju prirodno, ovo ne vrijedi: za njih vrijedi tzv. BENFORDOV ZAKON. Tako se brojevi od 1 do 9 pojavljuju u prosjeku kao prve značajne znamenke ovako:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
30.1% |
17.6% |
12.5% |
9.7% |
7.9% |
6.7% |
5.8% |
5.1% |
4.6% |
Povijest Benfordovog zakona
Ovu zanimljivu činjenicu otkrio je 1881. god. američki astronom Simon Newcomb. U to vrijeme džepni kalkulator nije postojao ni u najluđim snovima. Računanje se provodilo samo uz pomoć papira i olovke. Knjige sa stranicama i stranicama logaritamskih tablica upotrebljavale su se za složene račune. Newcomb je primijetio da su stranice logaritamskih tablica koje počinju s 1 puno istrošenije i češće upotrebljavane nego druge. Poslije analiziranja više skupina podataka koji se pojavljuju u prirodi, Newcomb je došao do teze koja je kasnije prozvana Benfordovim zakonom. Newcomba su, na žalost, u njegovo vrijeme ignorirali.Godine 1938. fizičar Frank Benford uočio je isto što i Newcomb. Međutim, on je proučavao mnogo veće skupine podataka nego Newcomb (čak 20.229 skupina različitih podataka).
Benford je proučavao brojevne podatke iz najrazličitijih izvora: površine jezera, duljine rijeka, brojnost populacija, atomske težine, statistike o baseballu, brojeve u telefonskom imeniku. I za sve podatke uočio je da se najčešće kao prva znamenka pojavljuje broj 1, zatim broj 2 i tako dalje. Za razliku od Newcomba, Benfordov rad bio je priznat i po njemu se odnosi koje je odredio zovu Benfordovim zakonom.
Sljedeća tablica pokazuje relativne frekvencije prvih znamenaka u različitim skupinama podataka, a Benford ju je objavio 1938. godine u svom originalnom radu.
|
|
|
Prva znamenka |
|
||||||||
|
Stu. |
Naziv |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
Uzorak |
|
A |
Rijeke, površina |
31.0 |
16.4 |
10.7 |
11.3 |
7.2 |
8.6 |
5.5 |
4.2 |
5.1 |
335 |
|
B |
Stanovništvo |
33.9 |
20.4 |
14.2 |
8.1 |
7.2 |
6.2 |
4.1 |
3.7 |
2.2 |
3259 |
|
C |
Konstante |
41.3 |
14.4 |
4.8 |
8.6 |
10.6 |
5.8 |
1.0 |
2.9 |
10.6 |
104 |
|
D |
Novine |
30.0 |
18.0 |
12.0 |
10.0 |
8.0 |
6.0 |
6.0 |
5.0 |
5.0 |
100 |
|
E |
Specifična toplina |
24.0 |
18.4 |
16.2 |
14.6 |
10.6 |
4.1 |
3.2 |
4.8 |
4.1 |
1389 |
|
F |
Tlak |
29.6 |
18.3 |
12.8 |
9.8 |
8.3 |
6.4 |
5.7 |
4.4 |
4.7 |
703 |
|
G |
H. P. gubitak |
30.0 |
18.4 |
11.9 |
10.8 |
8.1 |
7.0 |
5.1 |
5.1 |
3.6 |
690 |
|
H |
Molekularna težina |
26.7 |
25.2 |
15.4 |
10.8 |
6.7 |
5.1 |
4.1 |
2.8 |
3.2 |
1800 |
|
I |
Isušivanje |
27.1 |
23.9 |
13.8 |
12.6 |
8.2 |
5.0 |
5.0 |
2.5 |
1.9 |
159 |
|
J |
Atomska težina |
47.2 |
18.7 |
5.5 |
4.4 |
6.6 |
4.4 |
3.3 |
4.4 |
5.5 |
91 |
|
K |
n -1,
|
25.7 |
20.3 |
9.7 |
6.8 |
6.6 |
6.8 |
7.2 |
8.0 |
8.9 |
5000 |
|
L |
Dizajn |
26.8 |
14.8 |
14.3 |
7.5 |
8.3 |
8.4 |
7.0 |
7.3 |
5.6 |
560 |
|
M |
Reader's Digest |
33.4 |
18.5 |
12.4 |
7.5 |
7.1 |
6.5 |
5.5 |
4.9 |
4.2 |
308 |
|
N |
Cijene |
32.4 |
18.8 |
10.1 |
10.1 |
9.8 |
5.5 |
4.7 |
5.5 |
3.1 |
741 |
|
O |
Rendgenska voltaža |
27.9 |
17.5 |
14.4 |
9.0 |
8.1 |
7.4 |
5.1 |
5.8 |
4.8 |
707 |
|
P |
Statistika u baseballu |
32.7 |
17.6 |
12.6 |
9.8 |
7.4 |
6.4 |
4.9 |
5.6 |
3.0 |
1458 |
|
Q |
Vodljivost |
31.0 |
17.3 |
14.1 |
8.7 |
6.6 |
7.0 |
5.2 |
4.7 |
5.4 |
1165 |
|
R |
Adrese |
28.9 |
19.2 |
12.6 |
8.8 |
8.5 |
6.4 |
5.6 |
5.0 |
5.0 |
342 |
|
S |
n1, n2, ..., n! |
25.3 |
16.0 |
12.0 |
10.0 |
8.5 |
8.8 |
6.8 |
7.1 |
5.5 |
900 |
|
T |
Stopa smrtnosti |
27.0 |
18.6 |
15.7 |
9.4 |
6.7 |
6.5 |
7.2 |
4.8 |
4.1 |
418 |
|
|
Prosjek |
30.6 |
18.5 |
12.4 |
9.4 |
8.0 |
6.4 |
5.1 |
4.9 |
4.7 |
1011 |
|
|
Vjerojatna pogreška |
± 0.8 |
± 0.4 |
± 0.4 |
± 0.3 |
± 0.2 |
± 0.2 |
± 0.2 |
± 0.3 |
|
|
Podatke s kojima radimo i kojima se koristimo u istraživanju nazivamo uzorcima. Broj koji govori koliko se puta neki element pojavio u uzorku nazivamo frekvencijom. Nas će, međutim, zanimati zapravo relativna frekvencija, a to je omjer frekvencije i veličine uzorka.
Na primjer, ako promatramo
površine 200 jezera (uzorak) i
među njima ustanovimo da 62 jezera (frekvencija)
imaju znamenku 1 kao početnu znamenku, tada
je relativna frekvencija pojavljivanja znamenke 1 u površinama jezera
kao početne znamenke
Primjeri Benfordovog zakona
Uzmimo neki grad u Hrvatskoj koji ima 10 000 stanovnika i pretpostavimo da mu se broj stanovnika poveća godišnje za 2%. Za 36 godina broj stanovnika tog grada doseći će broj od
U narednih 15 godina
broj stanovnika povećat će se do
|
Početna znamenka |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Broj godina |
36 |
20 |
15 |
11 |
9 |
8 |
7 |
5 |
6 |
Sada pogledajmo nalazimo li u matematici negdje relativne frekvencije početnih znamenki kao u Benfordovom zakonu. Zanimljivo je, npr., pitanje koja je vjerojatnost da početna znamenka Fibonaccijevog broja bude 1? Ili da bude npr. 5? Ako ste u nedoumici vrijedi li Benfordov zakon za Fibonaccijeve brojeve ili ne, pogledajmo tablicu za prvih 100 Fibonaccijevih brojeva i njihove početne znamenke.
|
Početna znamenka |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Frekvencija |
30 |
18 |
13 |
9 |
8 |
6 |
5 |
7 |
4 |
Pogledajmo sad vremena trkača na 400 m - ne počinju mnoga od njih s 1. Pogledajmo godine poznatih političara u svijetu i kod nas - ni mnoga od njih ne počinju s 1 (zapravo skoro da i nema nikoga s npr. 19 godina). Za razliku od lutrije, gdje su podatci uniformno distribuirani i potpuno slučajni, ovi podatci nisu slučajni, nego su jako ograničeni i determinirani, tj. raspon mogućnosti preuzak je da bi dozvolio da se Benfordov zakon održi.
Drugim riječima, Benfordov zakon treba podatke koji nisu ni potpuno slučajni niti su jako ograničeni, već nešto između. Ti podatci mogu biti jako široki i tipični su rezultati više procesa s mnogo utjecaja, kao npr. populacija gradova koja može doseći razinu od desetak tisuća do nekoliko milijuna i ovisi o velikom rasponu faktora. Matematičari su otkrili da što veću količinu podataka imamo i što više podatci variraju, to se relativne frekvencije brojeva više približavaju relativnim frekvencijama iz Benfordovog zakona.
Pogledajmo sada kako su
logaritmi brojeva 1, 2, 3, ... , 9 distrubuirani unutar segmenta
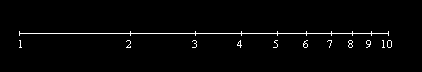
Logaritamska skala |
||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
30.1% |
17.6% |
12.5% |
9.7% |
7.9% |
6.7% |
5.8% |
5.1% |
4.6% |
P = (log10(n + 1) - log10(n)) / (log1010 - log101) = log10(n + 1) - log10(n) = log10(1+1/n),
gdje je n prva značajna znamenka broja.Tako je vjerojatnost da 1 bude prva značajna znamenka jednaka log10(2) = 0.3010, tj. 30.1%.
Za 2, 3, 4, ..., 9 uvrštavanjem u prethodnu formulu dobivaju se sljedeće vrijednosti:
Izvod Benfordovog zakona
Pokažimo da je frekvencija pojavljivanja prve znamenke u geometrijskom nizu qn upravo kao u Benfordovom zakonu ako je log q pozitivan iracionalan broj.Uzmimo da je prva znamenka od qn jednaka k. Tada je
qn
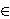 [k
[k 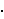 10m,
(k + 1)
10m,
(k + 1) 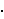 10m
10m 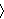 ,
m
,
m
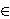
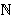 ,
k
,
k 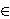 {1, 2, 3, 4, 5, 6, 7, 8, 9}
{1, 2, 3, 4, 5, 6, 7, 8, 9}
 n log10 q
n log10 q
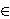 [log10 k + m,
log10 (k + 1) + m
[log10 k + m,
log10 (k + 1) + m
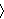 .
.
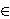 [0,1],
ova relacija ekvivalentna je s
[0,1],
ova relacija ekvivalentna je s
n log10 q
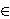 [log10 k,
log10 (k + 1)
[log10 k,
log10 (k + 1)
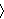 mod 1,
mod 1,
Navedimo sada (bez dokaza) jednu lemu iz teorije vjerojatnosti koju ćemo iskoristiti u daljnjem izvodu.
Lema: Ako je 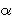 iracionalan broj, onda je frekvencija kojom niz
(n
iracionalan broj, onda je frekvencija kojom niz
(n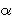 ),
n
),
n 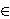
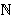 ,
pada u interval
,
pada u interval
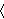 a,
b
a,
b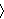
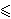 a <
b < 1,
a <
b < 1,
Sada, znači, imamo da je u
našem slučaju frekvencija kojom
nlog10 q
pada u interval
[log10 k,
log10 (k + 1)
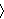 mod 1
jednaka
mod 1
jednaka
log10(k + 1) - log10k = log10 (1 + 1/k).
Dakle, dobili smo frekvencije kao u Benfordovom zakonu jer je frekvencija pojavljivanja znamenke k = 1 kao prve znamenke u geometrijskom nizu qn jednaka log10 2 = 0.301, za k = 2 je log10 (1 + 1/k) = 0.176 , ... , za k = 9 je log10 (1 + 1/k) = 0.046.Vidjeli smo da je frekvencija pojavljivanja znamenki u Benfordovom zakonu upravo logaritamska.
Ovaj izvod pokazuje zašto Fibonaccijevi brojevi poštuju Benfordov zakon. Naime, svaki
Fibonaccijev broj Fn može se
izraziti eksplicitno kao funkcija od n, naime Fn
je najbliži prirodan broj broju
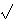 5)
5) 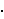
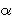
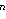 ,
,
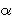 =
(1 +
=
(1 + 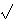 5)/2
5)/2
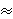 1.61803.
Kako je
1.61803.
Kako je 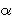 iracionalan broj, prema provedenom izvodu slijedi da se frekvencije početnih
znamenki kod Fibonaccijevih brojeva ponašaju u skladu s Benfordovim zakonom,
tj. frekvencija pojavljivanja početne znamenke je logaritamska.
iracionalan broj, prema provedenom izvodu slijedi da se frekvencije početnih
znamenki kod Fibonaccijevih brojeva ponašaju u skladu s Benfordovim zakonom,
tj. frekvencija pojavljivanja početne znamenke je logaritamska.
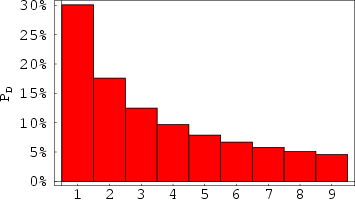
Za bazu 10, tj. dekadski sustav, vrijedi Benfordov zakon. Sljedeća slika pokazuje kako to izgleda u bazama 2, 3, 4, 5, ..., 10. Na x–osi nalaze se znamenke, a na y– osi vjerojatnost da ta znamenka bude prva značajna znamenka u broju u pripadnoj bazi (vjerojatnosti za određenu bazu obojane su različitim bojama).
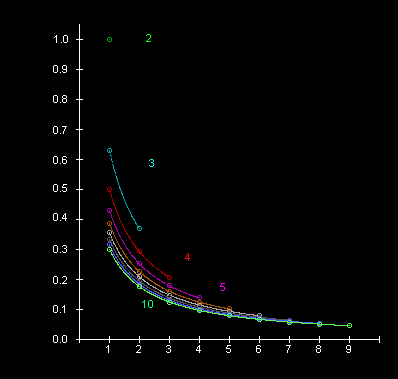
Benfordov zakon ne vrijedi za drugu značajnu znamenku u broju pa je tako vjerojatnost da će 1 biti druga značajna znamenka u broju jednaka 0.1138, a vjerojatnost da će 1 biti neka manje značajna znamenka u broju približava se 0.10 kako idemo dalje, tj. nakon prve značajne znamenke za koju vrijedi Benfordova raspodjela, znamenke počinju biti uniformno distribuirane.
Zaključak
Ako se pitate da li bi Benfordov zakon uopće mogao biti koristan i gdje, odgovor je da sve više matematičara, a i informatičara, drži da je Benfordov zakon snažan i relativno jednostavan alat za otkrivanje računovodstvenih prijevara, lažiranja podataka kod plaćanja poreza i čak za otkrivanja računalnih bugova. Porezne uprave nekoliko država, kao npr. Kalifornije, već koriste računalne programe za otkrivanje prijevara bazirane na Benfordovom zakonu, kao i neke velike svjetske kompanije. Dr. Nigrin sa sveučilišta u Dallasu, jedan od vodećih stručnjaka i znanstvenik koji je stekao priznanja za otkrivanje praktične upotrebe Benfordovog zakona, uvjeren je, kao i mnogi drugi stručnjaci, kako će Benfordov zakon u budućnosti biti sve češće primjenjivan u različite svrhe. Jedan od najranijih eksperimenata koje je proveo dr. Nigrin s programom koji se bazira na Benfordovom zakonu, bila je analiza porezne prijave predsjednika Clintona. Utvrdio je kako prijava sadrži vjerojatno zaokružene vrijednosti, a ne precizne brojeve, ali da nije lažna, tj. da nema porezne prijevare. Kako on kaže: "Benford je za mene veliki junak. Njegov zakon nije magičan, ali se katkad čini takvim!"Literatura
[1] K. Brown: Benford's Law, MathPageshttp://www.mathpages.com/home/kmath302/kmath302.htm
[2] E. Weisstein: Benford's Law, MathWorld
http://mathworld.wolfram.com/BenfordsLaw.html
[3] Benford's Law - How to Spot Tax Fraud,
Amazing Applications of Probability and Statistics
http://www.intuitor.com/statistics/Benford'sLaw.html
[4] J. Walthoe, R. Hunt, M. Pearson: Looking out
for number one, +plus magazine, September 1999
http://plus.maths.org/issue9/features/benford
[5] R. Knott: The Mathematical Magic of the Fibonacci Numbers
http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibmaths.html
Uvod
Povijest Benfordovog zakona
Primjeri Benfordovog zakona
Izvod Benfordovog zakona
Zaključak
Literatura