


14. DRŽAVNO NATJECANJE MLADIH MATEMATIČARA REPUBLIKE HRVATSKE
Omišalj, 4. - 7. svibnja 2005.
Zadaci za III. razred
- Nađite sva rješenja k, l, m
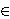
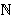 jednadžbe:
jednadžbe:
k! l! = k! + l! + m! .
(n! označava umnožak prirodnih brojeva od 1 do n.) - Upisana kružnica trokuta ABC dodiruje stranice
AC,
BC i
AB
redom u točkama M, N i R. Neka je S točka na manjem od dva luka
MN i t tangenta na taj luk s diralištem S.
Tangenta t siječe
NC i
MC
redom u točkama P i Q. Dokažite da se pravci AP, BQ, SR i MN
sijeku u jednoj točki.
- Odredite skup svih točaka triedra takvih da je zbroj
njihovih udaljenosti od strana triedra jednak zadanom
pozitivnom broju a.
- Pravilni poligon s 2005 stranica ima vrhove obojane crvenom,
bijelom i plavom bojom. "Dozvoljenim bojanjem" zovemo
bojanje u kojem dva susjedna vrha, koja su obojana različitim bojama,
obojimo trećom bojom.
(a) Dokažite da postoji konačan niz "dozvoljenih bojanja" nakon kojeg su svi vrhovi poligona iste boje.
(b) Je li ta boja jednoznačno određena početnim rasporedom boja vrhova?
