


14. DRŽAVNO NATJECANJE MLADIH MATEMATIČARA REPUBLIKE HRVATSKE
Omišalj, 4. - 7. svibnja 2005.
Zadaci za II. razred
- Neka su a, b, c realni brojevi,
a
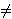 0.
Ako je x1 jedno rješenje jednadžbe
0.
Ako je x1 jedno rješenje jednadžbe
ax2 + bx + c = 0
i x2 jedno rješenje jednadžbe-ax2 + bx + c = 0,
dokažite da je tada jedno rješenje x3 jednadžbea/2
između x1 i x2, tj. x1 x2 + bx + c = 0
x2 + bx + c = 0
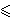 x3
x3
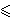 x2
ili
x2
x2
ili
x2 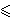 x3
x3
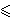 x1.
x1.
- Središte U upisane kružnice trokuta ABC spojeno je dužinama s
njegovim vrhovima. Neka su O1, O2 i
O3 središta kružnica opisanih trokutima BCU, CAU i ABU.
Dokažite da kružnice opisane trokutima
ABC iO1O2O3 imaju zajednično središte. - Ako su a, b i c realni brojevi veći od 1,
dokažite da za svaki realni broj r vrijedi jednakost
(loga bc)r + (logb ac)r + (logc ab)r
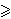 3
3  2r .
2r .
- Dokažite da u svakom skupu od 11 prirodnih brojeva postoji njih 6, čiji je zbroj djeljiv sa 6.
