13. DRŽAVNO NATJECANJE MLADIH MATEMATIČARA REPUBLIKE HRVATSKE

Trogir, 5. - 8. svibnja 2004.

Zadaci za II. razred

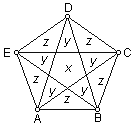
1. Pojedini dijelovi pravilnog peterokuta ABCDE imaju površine označene sa x, y, z, kao na slici. Ako je zadana površina x, nađite površine y i z, te površinu cijelog peterokuta.

   

2. Dokažite da za pozitivne brojeve a, b, c vrijedi nejednakost

   

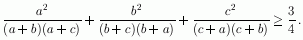
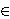
3. Brojevi (p_n) za n 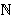definirani su na sljedeći način:
   p₁ = 2 i za n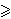 2, p_n je najveći prosti djelitelj od p₁ p₂ ... p_{n -1} + 1. Dokažite da je p_n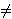 5 za svaki n .

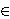
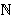4. Žaba skače to točkama koordinatne mreže počevši od točke (1,1) po sljedećim pravilima:
       (i)   iz točke (a, b) žaba smije skočiti u točku (2a, b), odnosno (a, 2b);
       (ii)   ako je a > b, žaba smije skočiti iz (a, b) u (a - b, b), ako je a < b, žaba smije skočiti iz (a, b) u (a, b - a).
   Može li žaba stići u točku
   (a)   (24,40),
   (b)   (40,60),
   (c)   (24,60),
   (d)   (200,4)?