



45. MEĐUNARODNA MATEMATIČKA OLIMPIJADA
Atena, Grčka, 4. - 18. srpnja 2004.
Zadaci
- (Rumunjska)
Neka je ABC šiljastokutan trokut takav da je
|AB|
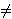 |AC|.
Kružnica kojoj je promjer
BC
siječe stranice
AB i
AC
u točkama M i N, tim redom.
Polovište stranice
BC
je točka O. Sjecište simetrala kutova
BAC i MON je točka R. Dokažite da se kružnice
opisane trokutima BMR i CNR sijeku u točki na stranici
BC.
|AC|.
Kružnica kojoj je promjer
BC
siječe stranice
AB i
AC
u točkama M i N, tim redom.
Polovište stranice
BC
je točka O. Sjecište simetrala kutova
BAC i MON je točka R. Dokažite da se kružnice
opisane trokutima BMR i CNR sijeku u točki na stranici
BC.
- (Koreja)
Odredite sve polinome P(x) s realnim
koeficijentima koji zadovoljavaju jednakost
P(a - b) + P(b - c) + P(c - a) = 2 P(a + b + c)
za sve realne brojeve a,b,c takve da je ab + bc + ca = 0. - (Estonija)
Neka je kuka figura koja je načinjena od
šest jediničnih kvadrata kao na slici
ili bilo koja figura dobivena od ove figure primjenom rotacija i osnih simetrija.
Odredite sve m × n pravokutnike koji se mogu pokriti kukama tako da:
- pravokutnik bude pokriven bez praznina i bez preklapanja;
- nijedan dio kuke ne bude izvan pravokutnika.
- (Koreja)
Neka je n ≥ 3 prirodan broj.
Neka su t1, t2, ... ,
tn pozitivni realni brojevi takvi da je
Dokaži da su ti, tj, tk duljine stranica trokuta za sve i,j,k takve da je 1 ≤ i < j < k ≤ n.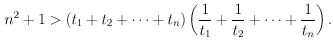
- (Poljska)
U konveksnom četverokutu ABCD dijagonala
BD nije simetrala niti kuta ABC niti kuta CDA.
Točka P je unutar kvadrata ABCD takva da je
Dokažite da je ABCD tetivni četverokut ako i samo ako je |AP| = |CP|. PBC =
PBC =
 DBA
i
DBA
i
 PDC =
PDC =
 BDA.
BDA.
- (Iran)
Prirodan broj nazivamo alternirajući
ako su mu svake dvije susjedne znamenke u decimalnom prikazu
različite parnosti.
Odredite sve prirodne brojeve n takve da postoji alternirajući višekratnik od n.
