
Hrvatski matematički elektronski časopis math.e

|
Hrvatski matematički elektronski časopis math.e |
| http://web.math.hr/mathe/ |
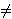 |AC|.
Kružnica kojoj je promjer
BC
siječe stranice
AB i
AC
u točkama M i N, tim redom.
Polovište stranice
BC
je točka O. Sjecište simetrala kutova
BAC i MON je točka R. Dokažite da se kružnice
opisane trokutima BMR i CNR sijeku u točki na stranici
BC.
|AC|.
Kružnica kojoj je promjer
BC
siječe stranice
AB i
AC
u točkama M i N, tim redom.
Polovište stranice
BC
je točka O. Sjecište simetrala kutova
BAC i MON je točka R. Dokažite da se kružnice
opisane trokutima BMR i CNR sijeku u točki na stranici
BC.
P(a - b) + P(b - c) + P(c - a) = 2 P(a + b + c)
za sve realne brojeve a,b,c takve da je ab + bc + ca = 0.

Odredite sve m × n pravokutnike koji se mogu pokriti kukama tako da:
 PBC =
PBC =
 DBA
i
DBA
i
 PDC =
PDC =
 BDA.
BDA.