


7. MEDITERANSKO MATEMATIČKO NATJECANJE
Zagreb, 24. travnja 2004.
Zadaci
- Nađite sve prirodne brojeve m takve da je
1!
 3!
3!
 5!
5!
 ...
...
 (2m -1)! =
(m(m + 1)/2)! .
(2m -1)! =
(m(m + 1)/2)! .
- Pravac na kojem leži visina iz vrha A trokuta ABC
siječe opisanu mu kružnicu u točki T.
Promjer opisane kružnice kroz točku A i pravac OT
(O je središte opisane kružnice)
sijeku stranicu
BC
u Q i M, tim redom.
Pokažite da jeP(AQC) / P(CMT) = (sin B / cos C)2 ,
(P(XYZ) je površina trokuta XYZ). - Ako su a, b, c pozitivni brojevi
takvi da je
1 = ab + bc + ca + 2abc,
dokažite nejednakost2(a + b + c) + 1
Kada vrijedi znak jednakosti?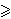 32abc.
32abc.
- Neka su z1,
z2,
z3 u parovima različiti
kompleksni brojevi za koje je
|z1| = |z2| = |z1| = 1,
i vrijedi jednakost1/(2+|z1+z2|) + 1/(2+|z2+z3|) + 1/(2+|z3+z1|) = 1.
Ako su točke A(z1), B(z2), C(z3) vrhovi šiljastokutnog trokuta, dokažite da je on jednakostraničan.
