Hrvatski matematički elektronski časopis math.e

http://web.math.hr/mathe/

7. MEDITERANSKO MATEMATIČKO NATJECANJE

Zagreb, 24. travnja 2004.

Zadaci


  1. Nađite sve prirodne brojeve m takve da je

    1! * 3! * 5! * ... * (2m -1)! = (m(m + 1)/2)! .

  2. Pravac na kojem leži visina iz vrha A trokuta ABC siječe opisanu mu kružnicu u točki T. Promjer opisane kružnice kroz točku A i pravac OT (O je središte opisane kružnice) sijeku stranicu BC u Q i M, tim redom.
    Pokažite da je

    P(AQC) / P(CMT) = (sin B / cos C)2 ,

    (P(XYZ) je površina trokuta XYZ).

  3. Ako su a, b, c pozitivni brojevi takvi da je

    1 = ab + bc + ca + 2abc,

    dokažite nejednakost

    2(a + b + c) + 1 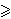>= 32abc.

    Kada vrijedi znak jednakosti?

  4. Neka su z1, z2, z3 u parovima različiti kompleksni brojevi za koje je

    |z1| = |z2| = |z1| = 1,

    i vrijedi jednakost

    1/(2+|z1+z2|) + 1/(2+|z2+z3|) + 1/(2+|z3+z1|) = 1.

    Ako su točke A(z1), B(z2), C(z3) vrhovi šiljastokutnog trokuta, dokažite da je on jednakostraničan.