


12. DRŽAVNO NATJECANJE MLADIH MATEMATIČARA REPUBLIKE HRVATSKE
Pula, 7. - 10. svibnja 2003.
Zadaci za III. razred
- U trokutu ABC je a = |BC|, b = |AC|, c =
|AB|,
 =
=
 CAB,
CAB,
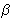 =
=
 ABC,
ABC,
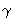 =
=
 BCA.
BCA.
a) Ako je =
3
=
3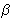 , dokažite da je
(a2 - b2)(a
- b) = bc2.
, dokažite da je
(a2 - b2)(a
- b) = bc2.
b) Da li vrijedi obrat? Obrazložite. - Dokažite jednakost
na svaki prirodan broj n > 2.![[n(m+1)/(4n-2)]=[(n+1)/4]](nn1.gif)
- Svi bridni kutovi pri vrhu D tetraedra ABCD jednaki su
 ,
a kutovi između dviju strana tetraedra kojima je jedan
vrh D jednaki su
,
a kutovi između dviju strana tetraedra kojima je jedan
vrh D jednaki su 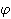 . Dokažite da postoji točno jedan kut
. Dokažite da postoji točno jedan kut
 za koji je
za koji je
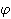 =
2
=
2 .
.
- Imamo 8 kockica duljine brida 1 čije su 24 strane obojene plavo, a preostalih 24 crveno. Dokažite da se od tih kockica može složiti kocka (2 × 2 × 2) na čijem oplošju će biti jednak broj plavih i crvenih kvadrata (1 × 1).
