
Hrvatski matematički elektronski časopis math.e

|
Hrvatski matematički elektronski časopis math.e |
| http://web.math.hr/mathe/ |
 =
=
 CAB,
CAB,
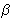 =
=
 ABC,
ABC,
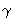 =
=
 BCA.
BCA.  =
3
=
3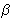 , dokažite da je
(a2 - b2)(a
- b) = bc2.
, dokažite da je
(a2 - b2)(a
- b) = bc2.
![[n(m+1)/(4n-2)]=[(n+1)/4]](nn1.gif)
 ,
a kutovi između dviju strana tetraedra kojima je jedan
vrh D jednaki su
,
a kutovi između dviju strana tetraedra kojima je jedan
vrh D jednaki su 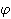 . Dokažite da postoji točno jedan kut
. Dokažite da postoji točno jedan kut
 za koji je
za koji je
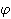 =
2
=
2 .
.