11. DRŽAVNO NATJECANJE MLADIH MATEMATIČARA REPUBLIKE HRVATSKE

Zadar, 2. - 5. svibnja 2002.

Zadaci za III. razred

1. U trokutu ABC kutovi = BAC i 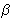= CBA su šiljasti. S vanjske strane trokuta, nad stranicama AC i BC kao bazama, konstruirani su jednakokračni trokuti ACD i BCE s vršnim kutovima ADC = 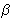, odnosno BEC = . Neka je O središte kružnice opisane trokutu ABC. Dokažite da je |DO| + |EO| jednako opsegu trokuta ABC ako i samo ako je kut ACB pravi.

2. Dokažite da se prirodan broj može prikazati kao zbroj dva ili više uzastopnih prirodnih brojeva ako i samo ako taj broj nije potencija broja 2.

3. Na dijagonalama AB₁ i CA₁ bočnih strana ABB₁A₁ i CAA₁C trostrane prizme ABCA₁B₁C₁ dane su točke E i F takve da je EF 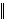BC₁. Nađite omjer duljina dužina EF i BC₁.

4. Na otoku živi n domorodaca. Svaka dva su ili prijatelji ili neprijatelji. Jednog dana poglavica naredi svim stanovnicima (uključujući i sebe) da si naprave i da nose kamene ogrlice, tako da svaka dva prijatelja imaju barem po jedan istovrsni kamen u svojim ogrlicama, a da se sva kamenja u ogrlicama dvaju neprijatelja razlikuju. (Ogrlica može biti i bez kamenja.) Dokažite da se poglavičina zapovijed može izvršiti koristeći [n²/4] različitih vrsta kamenja, i da se općenito ovo ne može postići s manje kamenja.