
Hrvatski matematički elektronski časopis math.e

|
Hrvatski matematički elektronski časopis math.e |
| http://web.math.hr/mathe/ |
 =
=  BAC i
BAC i
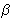 =
=
 CBA su šiljasti.
S vanjske strane trokuta, nad stranicama
AC i
BC kao bazama,
konstruirani su jednakokračni trokuti ACD i BCE s vršnim kutovima
CBA su šiljasti.
S vanjske strane trokuta, nad stranicama
AC i
BC kao bazama,
konstruirani su jednakokračni trokuti ACD i BCE s vršnim kutovima
 ADC
=
ADC
= 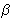 , odnosno
, odnosno
 BEC
=
BEC
=  . Neka je O
središte kružnice opisane trokutu ABC. Dokažite da je |DO| + |EO|
jednako opsegu trokuta ABC ako i samo ako je kut
. Neka je O
središte kružnice opisane trokutu ABC. Dokažite da je |DO| + |EO|
jednako opsegu trokuta ABC ako i samo ako je kut
 ACB pravi.
ACB pravi.
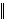 BC1. Nađite omjer duljina dužina
EF i BC1.
BC1. Nađite omjer duljina dužina
EF i BC1.