43. MEĐUNARODNA MATEMATIČKA OLIMPIJADA

Glasgow, Velika Britanija, 19. - 30. srpnja 2002.

Zadaci

1. (Kolumbija) Neka je n pozitivan cijeli broj. Označimo s T skup točaka (x,y) u ravnini za koje su x i y nenegativni cijeli brojevi i x + y < n. Svaka točka iz skupa T obojana je crveno ili plavo. Ako je točka (x,y) obojana creveno, takve su i sve točke (x',y') iz skupa T za koje je x' 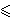x i y' 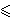y. Skup od n plavih točaka s međusobno različitim x-koordinatama nazovimo X-skup, a skup od n plavih točaka s međusobno različitim y-koordinatama nazivamo Y-skup. Dokažite da je broj X-skupova jednak broju Y-skupova.

2. (Koreja) Neka je BC promjer kružnice 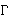sa središtem u točki O. Označimo s A točku na 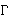takvu da je 0^o < AOB < 120^o. Neka je D polovište luka AB koji ne sadrži točku C. Pravac koji prolazi kroz točku O i paralelan je s DA siječe pravac AC u točki J. Simetrala dužine OA siječe kružnicu 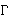u točkama E i F. Dokažite da je J središte trokutu CEF upisane kružnice.

3. (Rumunjska) Nađite sve parove (m,n) cijelih brojeva m, n 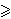3 za koje postoji beskonačno mnogo pozitivnih cijelih brojeva a takvih da je

   (a^m + a - 1) / (aⁿ + a² - 1)

   cijeli broj.

4. (Rumunjska) Neka je n prirodan broj veći od 1. Neka su d₁, d₂, ... , d_k svi pozitivni djelitelji broja n takvi da je

   1 = d₁ < d₂ < ... < d_k = n.

   Definirajmo D = d₁d₂ + d₂d₃ + ... + d_k-1d_k.
         (a) Dokažite da je D < n².
         (b) Odredite sve brojeve n za koje je D djelitelj broja n².

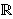
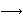
5. (Indija) Nađite sve funkcije f : 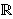, pri čemu je 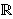skup realnih brojeva, takve da je

   (f(x) + f(z)) (f(y) + f(t)) = f(xy - zt) + f(xt + yz)

   za sve x, y, z, t iz .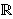

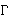
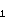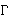
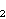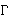
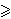6. (Ukrajina) Neka su , , ... , , kružnice polumjera 1 u ravnini, pri čemu je n 3. Označimo njihova središta redom s O₁, O₂, ... , O_n. Pretpostavimo da nijedan pravac nema zajedničkih točaka s više od dvije promatrane kružnice. Dokažite nejednakost