Hrvatski matematički elektronski časopis math.e

|
Hrvatski matematički elektronski časopis math.e |
| http://web.math.hr/mathe/ |
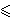 x
i y'
x
i y' 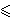 y.
Skup od n plavih točaka s međusobno različitim
x-koordinatama nazovimo X-skup, a skup od n
plavih točaka s međusobno različitim y-koordinatama nazivamo
Y-skup. Dokažite da je broj X-skupova jednak
broju Y-skupova.
y.
Skup od n plavih točaka s međusobno različitim
x-koordinatama nazovimo X-skup, a skup od n
plavih točaka s međusobno različitim y-koordinatama nazivamo
Y-skup. Dokažite da je broj X-skupova jednak
broju Y-skupova.
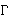 sa središtem u
točki O. Označimo s A točku na
sa središtem u
točki O. Označimo s A točku na
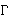 takvu da je
0o <
takvu da je
0o <
 AOB
< 120o.
Neka je D polovište luka AB koji ne sadrži točku C. Pravac koji
prolazi kroz točku O i paralelan je s DA siječe pravac AC u točki J.
Simetrala dužine OA
siječe kružnicu
AOB
< 120o.
Neka je D polovište luka AB koji ne sadrži točku C. Pravac koji
prolazi kroz točku O i paralelan je s DA siječe pravac AC u točki J.
Simetrala dužine OA
siječe kružnicu
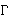 u točkama E i F.
Dokažite da je J središte trokutu CEF upisane kružnice.
u točkama E i F.
Dokažite da je J središte trokutu CEF upisane kružnice.
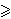 3 za koje postoji
beskonačno mnogo pozitivnih cijelih brojeva a takvih da je
3 za koje postoji
beskonačno mnogo pozitivnih cijelih brojeva a takvih da je
(am + a - 1) / (an + a2 - 1)
cijeli broj.
1 = d1 < d2 < ... < dk = n.
Definirajmo D = d1d2 + d2d3 + ... + dk-1dk.
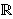
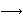
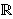 , pri čemu je
, pri čemu je
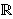 skup realnih brojeva, takve
da je
skup realnih brojeva, takve
da je
(f(x) + f(z)) (f(y) + f(t)) = f(xy - zt) + f(xt + yz)
za sve x, y, z, t iz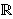 .
.
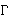
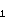 ,
,
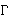
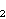 , ... ,
, ... ,
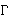
 , kružnice polumjera 1
u ravnini, pri čemu je n
, kružnice polumjera 1
u ravnini, pri čemu je n
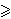 3.
Označimo njihova središta redom s O1,
O2, ... , On.
Pretpostavimo da nijedan pravac nema zajedničkih točaka s više
od dvije promatrane kružnice. Dokažite nejednakost
3.
Označimo njihova središta redom s O1,
O2, ... , On.
Pretpostavimo da nijedan pravac nema zajedničkih točaka s više
od dvije promatrane kružnice. Dokažite nejednakost