
| Nadrealni brojevi |  |  |
|
Sadržaj: 1. UvodZa sve postoji vrijeme i mjesto, pa tako i za izraze poput √ω − π. A budući da to vrijeme i mjesto nije kolegij Teorija skupova u zimskom semestru, vrijeme je da sami stvorimo prikladno mjesto. Nadrealni brojevi? Neobična kombinacija riječi, gotovo oksimoron, barem u svakodnevnom shvaćanju. Definiciju dugujemo Johnu Hortonu Conwayu, dok je sam naziv osmislio Donald Knuth. Ovi "novi" brojevi sadrže realne brojeve, no i mnogo, mnogo više - beskonačne ordinale, infinitezimalne vrijednosti i doslovno sve ono između. Dakle, naziv im sasvim dobro pristaje. Uostalom, nikad nije na odmet malo nadrealizma u matematici...  Salvador Dalí, Iskušenje sv. Antuna. Conway je na zamisao o nadrealnim brojevima došao prije nekoliko desetljeća, na Cambridge Universityju, dok je pokušavao naučiti igrati Go, izazovnu igru na ploči, popularnu u Kini i Japanu. Pažljivo promatranje uvjerilo ga je da se igra može tumačiti kao zbroj više manjih, jednostavnijih igara. Conway je primijenio istu logiku i na neke druge strateške igre, i došao do zaključka da se igre određenog tipa ponašaju kao brojevi s karakterističnim osobinama. Mi se ovdje nećemo dotaknuti igara, no o njima možete čitati u članku Matka Botinčana Kombinatorne igre [MB] koji je objavljen u 6. broju math.e. 2. Konstrukcija brojevaBrojeve je moguće zadati aksiomatski, kao što je to uobičajena praksa s realnim brojevima na uvodnim kolegijima u matematičku analizu. No, tada se postavlja pitanje postoji li uopće skup brojeva koji zadovoljava navedene aksiome? To pitanje, naravno, nije specifično za brojeve nego za bilo koju strukturu koju zadajemo aksiomatski. Kad su u pitanju realni brojevi, dva su najčešće spominjana načina na koji ih se može konstruirati od racionalnih brojeva: Dedekindovi rezovi i Cantorova konstrukcija s pomoću Cauchyjevih nizova. Konstrukcija nadrealnih brojeva ima sličnosti s konstrukcijom realnih brojeva s pomoću Dedekindovih rezova. Razlika je u tome što ne pretpostavljamo da su racionalni brojevi već konstruirani nego sve brojeve konstruiramo na isti način. Osnovna ideja konstrukcije je jednostavna, ali djeluje pomalo zbunjujuće pri prvom susretu. Evo kako je tu ideju opisao Donald Knuth u svojoj matematičkoj noveli [DK]. U početku bijaše praznina, i J. H. W. H. Conway poče stvarati brojeve. Conway reče: "Neka budu dva pravila koja će iznjedriti sve brojeve, velike i male. Ovo neka bude prvo pravilo: Svaki broj odgovara dvama skupovima prethodno stvorenih brojeva, takvima da nijedan element lijevog skupa nije veći ili jednak nijednom elementu desnog skupa. A drugo pravilo neka bude: Broj je manji ili jednak drugom broju ako i samo ako nijedan element lijevog skupa prvog broja nije veći ili jednak drugom broju, i nijedan element desnog skupa drugog broja nije manji ili jednak prvom broju." I vidje Conway da su pravila dobra. Dakle, da utvrdimo:
Ovako ćemo označavati brojeve:
x = {XL | XR},
gdje su XL i XR lijevi i desni skup
broja x. Zahtjev koji imamo na njih jest:
za svaki xL ∈ XL
i za svaki xR ∈ XR vrijedi
xL
To, pak, zapisano simbolički izgleda ovako: 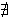 xL ∈ XL :
xL ≥ y )
i
( xL ∈ XL :
xL ≥ y )
i
( 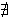 yR ∈ YR :
yR ≤ x ). yR ∈ YR :
yR ≤ x ).Sada imamo nadrealne brojeve definirane u terminima nadrealnih brojeva i relacije "manji ili jednak", koja je također zadana rekurzivno. Unatoč tomu, nema razloga za paniku! U ovom članku nećemo davati formalnu definiciju nadrealnih brojeva jer ona zahtijeva dublje poznavanje teorije skupova (naprimjer transfinitnu indukciju i teorem rekurzije). Nadamo se da će ideja konstrukcije postati jasnija kroz primjere i tvrdnje koje slijede. Nove brojeve stvaramo od onih već stvorenih pa je na početku, kada nemamo nijedan prethodno konstruirani broj, prirodno da nam ulogu lijevog i desnog skupa preuzme prazan skup. Prvi stvoreni broj izgleda ovako: {Ø | Ø}. Zapravo, prije nego što ustvrdimo da to jest broj, moramo provjeriti uvjet iz definicije. No uistinu, nijedan element praznog skupa nije veći ili jednak nijednom elementu praznog skupa (jer prazan skup nema elemenata), pa je uvjet zadovoljen. Taj broj zovemo "nula" i skraćeno ćemo ga pisati kao 0, tj. 0 ≡ {Ø | Ø}. Bilo bi zgodno kada bi vrijedilo 0 ≤ 0, no sada smo u novom okruženju, i tu tvrdnju moramo sami provjeriti. Propozicija 1. 0 ≤ 0. Dokaz. Ono što tvrdimo jest {Ø | Ø} ≤ {Ø | Ø}. Izravno iz definicije slijedi da je to ekvivalentno zahtjevima da ne postoji element praznog skupa koji je veći ili jednak od nule i da ne postoji element praznog skupa koji je manji ili jednak od nule, što zasigurno vrijedi. ■ Sada kada znamo jedan nadrealan broj, možemo ga iskoristiti kako bismo došli do novih brojeva, tako da stavimo nulu kao element lijevog ili desnog skupa: {0 | Ø}, {Ø | 0}, {0 | 0}. Međutim, {0 | 0} nije broj jer, prema maloprije dokazanom, vrijedi 0 ≤ 0. Pogledajmo kako se naša nova dva broja odnose prema nuli. Propozicija 2. 0 ≤ {0 | Ø}. Dokaz. Potrebno je vidjeti da ne postoji element praznog skupa koji je veći ili jednak od broja {0 | Ø} i da ne postoji element praznog skupa koji je manji ili jednak od 0. Budući da je i jedno i drugo istinito, slijedi tvrdnja. ■ Na isti način sami možete dokazati sljedeću tvrdnju. Zadatak 1. {Ø | 0} ≤ 0. Brojeve {0 | Ø} i {Ø | 0} zvat ćemo "jedan" i "minus jedan". Skraćeno ćemo ih zapisivati simbolima 1 i −1, tj. 1 ≡ {0 | Ø}, −1 ≡ {Ø | 0}. Znamo tri nadrealna broja i s pomoću njih mozemo napraviti 61 par lijevog i desnog skupa. No, samo 17 od tih parova zadovoljava uvjet iz definicije nadrealnog broja: {−1 | Ø}, {Ø | −1}, {1 | Ø}, {Ø | 1}, {−1, 0 | Ø}, {−1 | 0}, {Ø | −1, 0}, {0, 1 | Ø}, {0 | 1}, {Ø | 0, 1}, {−1, 1 | Ø}, {−1 | 1}, {Ø | −1, 1}, {−1, 0, 1 | Ø}, {−1, 0 | 1}, {−1 | 0, 1}, {Ø | −1, 0, 1}.
Zadatak 2. Dokažite 0 < 1. Lako je dokazati da je 1 < {1 | Ø} i {Ø | −1} < −1, pa ćemo te brojeve zvati "dva" i "minus dva", odnosno 2 ≡ {1 | Ø}, −2 ≡ {Ø | −1}. Možda zanimljivije, može se dokazati 0 < {0 | 1} i {0 | 1} < 1, odnosno −1 < {−1 | 0} i {−1 | 0} < 0. Ove brojeve zovemo "jedna polovina" i "minus jedna polovina": ½ ≡ {0 | 1}, −½ ≡ {−1 | 0}. Na prvi pogled nije jasno zašto se baš koristimo s ½ i −½, a ne bilo kojim drugim brojevima između 0 i 1, odnosno −1 i 0. Odgovor se nalazi u 4. cjelini, gdje ćemo vidjeti da je {0 | 1} + {0 | 1} = 1. Promotrimo sada broj {−1 | 1}. Propozicija 3. 0 ≤ {−1 | 1}. Dokaz. Zapišimo 0 ponovno kao {Ø | Ø}. Tvrdnja je ekvivalentna sljedećem: ne postoji element praznog skupa koji je veći ili jednak od {−1 | 1} i 1 nije manji ili jednak od 0. Prvo trivijalno vrijedi, a drugi zahtjev slijedi iz Zadatka 2. ■ Zadatak 3. Dokažite {−1 | 1} ≤ 0. Iz Propozicije 3 i Zadatka 3 imamo 0 = {−1 | 1}. Primijetimo da je su ta dva broja jednaka, a ne identična, jer se kao skupovi očito razlikuju. Kažemo da su {Ø | Ø} i {−1 | 1} dva različita predstavnika broja 0. Slično se dokazuje da su svi do sada stvoreni brojevi jednaki jednom od ovih brojeva: 0, 1, −1, 2, −2, ½, −½. Jasno je kako bismo dalje nalazili nove brojeve služeći se starima. Također očekujemo da ćemo pritom naići na mnoge nove predstavnike već otkrivenih brojeva. Uvedimo još jedan novi pojam, rođendan nadrealnog broja.
Elemente iz XL i XR nekad zovemo roditeljima broja x. 3. Neka (osnovna) svojstvaTeorem 1. Ako je x nadrealan broj, onda je x ≤ x. Dokaz. Provodimo ga indukcijom po danu rođenja nadrealnog broja.
Bazu smo već dokazali: 0 ≤ 0.
Pretpostavimo da tvrdnja vrijedi za sve brojeve rođene prije x, odnosno
za sve elemente iz XL i XR.
Vrijedi x ≤ x ako i samo ako
ne postoji xL ∈ XL
takav da je x ≤ xL
i ne postoji xR ∈ XR
takav da je xR ≤ x.
Prvo dokazujemo lijevu stranu. Želimo dokazati da
x Kao posljedicu dobivamo još jednu "zgodnu" tvrdnju. Korolar 1. Ako je x nadrealan broj, onda je x = x. Teorem 2. Nadrealan broj veći je od svih elemenata svojeg lijevog skupa i manji od svih elemenata svojeg desnog skupa, odnosno a < {A | B} i {A | B} < b za sve a ∈ A i b ∈ B. Dokaz. Da bismo dokazali prvi dio, definicija relacije < zahtijeva da
dokažemo dvije tvrdnje: a ≤ {A | B} i
{A | B}  aL, aL,
što je dalje ekvivalentno s Ako izaberemo a' ≡ a, onda je aL ≤ a, za svaki aL ∈ AL. Ta tvrdnja identična je prvoj tvrdnji teorema, osim što su varijable zamijenjene nekim roditeljem svojeg lijevog skupa. Induktivno zaključujemo da prva tvrdnja vrijedi ako vrijedi za nadrealan broj kojemu je lijevi skup prazan, a to smo već provjerili. Analogno se dokazuje druga tvrdnja teorema, {A | B} < b za svaki b ∈ B. ■ Teorem 3. Ako je x ≤ y i y ≤ z, onda je x ≤ z. Dokaz.
Pretpostavimo suprotno: postoje nadrealni brojevi x, y,
z takvi da je x ≤ y i y ≤ z
i x 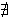 xL ∈ XL : y ≤ xL, xL ∈ XL : y ≤ xL,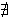 yR ∈ YR : yR ≤ x, yR ∈ YR : yR ≤ x,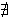 yL ∈ YL : z ≤ yL, yL ∈ YL : z ≤ yL,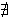 zR ∈ ZR : zR ≤ y, zR ∈ ZR : zR ≤ y,( ∃ xL ∈ XL : z ≤ xL ) ili ( ∃ zR ∈ ZR : zR ≤ x ). Imamo dva slučaja s obzirom na zadnju tvrdnju. Ako postoji xL ∈ XL takav da je z ≤ xL, onda je (y, z, xL) trojka brojeva s istim svojstvom koje ima trojka (x, y, z). Ako, pak, postoji zR ∈ ZR takav da je zR ≤ x, onda je (zR, x, y) takva trojka. U svakom slučaju, dolazimo do kontradikcije, jer ako je suma dana rođenja od x, y i z jednaka n, onda je suma dana rođenja nove trojke strogo manja od n. Tako možemo nastaviti dalje i po volji smanjiti sumu, no suma dana rođenja triju brojeva nikad nije manja od 3. ■ Teorem 4. Uređaj ≤ na nadrealnim brojevima je linearan, odnosno bar jedna od tvrdnji x ≤ y i y ≤ x je istinita. Dokaz. Ako x ≤ y ne vrijedi, to znači da je najmanje jedna od slijedećih dviju tvrdnji istinita: ∃ yR ∈ YR : yR ≤ x. Ako pretpostavimo da je prva tvrdnja istinita, možemo naći xL takav da je y ≤ xL. Nadalje, zbog Teorema 2 znamo da je xL ≤ x. Sada, koristeći Teorem 3 (svojstvo tranzitivnosti), dobivamo y ≤ x. Analogno postupamo kada pretpostavimo da je druga tvrdnja istinita. ■ Zadatak 4. Ako je x < y i y < z, onda je x < z. Sljedeći teorem će nam dopustiti da pojednostavnimo mnoge brojeve. Teorem 5. Ako nam je dan nadrealan broj x = {XL | XR}, možemo ukloniti bilo koji element iz XL osim najvećeg, a da ne promijenimo vrijednost broja x. Slično, možemo ukloniti bilo koji element iz XR osim najmanjeg, a da ne promijenimo vrijednost broja x. Dokaz. Dokazat ćemo prvi dio teorema, a drugi dio dokazuje se na isti način. Pretpostavimo da je x={x1, x2, ... | XR} i da je x1 < x2. Želimo dokazati da je {x1, x2, ... | XR} = {x2, ... | XR}, a to znači da moramo dokazati {x1, x2, ... | XR} ≤ {x2, ... | XR} i {x2, ... | XR} ≤ {x1, x2, ... | XR}. To se dalje razlaže na četiri tvrdnje: 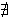 a ∈ {x1, x2, ...} : {x2, ... | XR} ≤ a, a ∈ {x1, x2, ...} : {x2, ... | XR} ≤ a,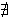 b ∈ XR : b ≤ {x1, x2, ... | XR}, b ∈ XR : b ≤ {x1, x2, ... | XR},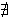 a' ∈ {x2, ...} : {x1, x2, ... | XR} ≤ a', a' ∈ {x2, ...} : {x1, x2, ... | XR} ≤ a',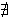 b' ∈ XR : b' ≤ {x2, ... | XR}. b' ∈ XR : b' ≤ {x2, ... | XR}.
Druga, treća i četvrta tvrdnja direktno slijede iz Teorema 2. Prva tvrdnja ekvivalentna je s  a, a,
što je, pak, ekvivalentno s Trebamo samo promotriti slučaj kada je a = x1 jer ostale vrijednosti broja a pokriva Teorem 2. Iz Teorema 2 imamo {x2, ... | XR} > x2, pa sada, budući da je x2 > x1 = a, prema svojstvu tranzitivnosti (Teorem 3) slijedi zadnja tvrdnja. ■ Uočite da skup nadrealnih brojeva ne mora imati niti najveći, niti najmanji element (u 5. cjelini razmatrat ćemo beskonačne skupove!), pa ne možemo zaključiti da XL i XR možemo svesti na jednočlane skupove za svaki nadrealan broj x = {XL | XR}. Korolar 2. Ako skup nadrealnih brojeva A ima najveći element amax, tada je {A | B} = {amax | B}. Slično, ako skup B ima najmanji element bmin, tada je {A | B} = {A | bmin}. Zadatak 5. Ako je nadrealni broj x veći od svih elemenata skupa A i manji od svih elemenata skupa B, tada je x = {XL ∪ A | XR ∪ B}. Teorem 6. Ako nakon dana m postoje nadrealni brojevi x1 < x2 < x3 < ... < xn, sve nove brojeve koji su rođeni na (m + 1).-vi dan možemo predstaviti s {Ø | x1}, {x1 | x2}, {x2 | x3}, ... , {xn−1 | xn}, {xn | Ø}. Nakon (m+1).-vog dana poredak stvorenih nadrealnih brojeva bit će: Dokaz. O brojevima rođenim na (m + 1).-vi dan teorem tvrdi slijedeće:
(1) {Ø | x1} i
{xn | Ø} su predstavnici
brojeva koji nisu bili poznati na dan m; Iz Teorema 2 znamo da je {Ø | x1} < x1. Budući da je x1 najmanji broj rođen na dan m, {Ø | x1} mora predstavljati novu vrijednost i njegova pozicija u skupu do tada stvorenih brojeva je očigledna. Analogno zaključujemo za {xn | Ø} i time je dokazano (1). Nadalje, iz Teorema 2 znamo da je xi < {xi | xj} < xj. Budući da na dan m nije postojao broj između xi i xj, {xi | xj} mora predstavljati novi broj. Ako je i + 1 < j, neka xk predstavlja najstariji nadrealni broj između xi + 1 i xj − 1. Ako postoji više jednako starih brojeva, neka je xk bilo koji od njih. Znamo da roditelji od xk moraju biti ili manji od xi + 1 ili veći od xj − 1 jer prije rođenja xk nije postojao nijedan broj između xi + 1 i xj − 1. Dakle, vrijedi XkL ≤ xi i xj ≤ XkR, gdje su XkL i XkR lijevi i desni skup broja xk. Sada iz xi < {xi | xj} < xj slijedi XkL < {xi | xj} < XkR, pa primjenom Zadatka 5 dolazimo do {xi | xj} = {xi, XkL | xj, XkR}. Primjenom Zadatka 5 na činjenicu xi < xk < xj dobivamo i xk = {xi, XkL | xj, XkR}. Slijedi {xi | xj} = xk. Usput smo dokazali i da postoji samo jedan najstariji broj između xi i xj, s obzirom da vrijednost takvog broja nužno mora biti jednaka {xi | xj}. Drugi dio teorema direktno proizlazi iz Teorema 2. ■ Još jednom ćemo istaknuti činjenicu dobivenu u dokazu Teorema 6 jer nam ona bitno olakšava računanje s nadrealnim brojevima. Korolar 2. Ako je x najstariji nadrealan broj između a i b, tada je {a | b} = x. 4. Zbrajanje, oduzimanje i množenjePrvo nekoliko uvodnih napomena. Sumu broja n i skupa brojeva S definiramo kao skup koji dobijemo dodavanjem broja n svakom elementu skupa S, tj. n + S = {n + s : s ∈ S}. Analogno definiramo razliku n − S i produkt n · S broja n i skupa S. Primijetimo da je n + Ø = Ø, n − Ø = Ø i n ·Ø = Ø. Sumu skupova S i T definiramo kao skup koji dobijemo zbrajanjem svakog elementa skupa S sa svakim elementom skupa T, tj. S + T = {s + t : s ∈ S, t ∈ T}. Sada možemo definirati zbrajanje nadrealnih brojeva i suprotan broj.
Zadatak 6. Dokažite da vrijedi 1 + ½ = 1½. Lako je vidjeti da je suprotan broj nadrealnog broja nadrealan broj, no pokazati da je zbroj dvaju nadrealnih brojeva ponovno nadrealan broj, nije tako trivijalno. Indukcijom i napornim raspisivanjem zajedno se dokazuju sljedeća dva teorema. Teorem 7. Ako je x ≤ x' i y ≤ y', onda je x + y ≤ x' + y'. Teorem 8. Ako je x + y ≥ x' + y' i y ≤ y', onda je x ≥ x'. Iz njih, pak, dalje proizlazi: Korolar 3. Ako je x = x' i y = y', onda je x + y = x' + y'. Teorem 9. Ako je x < x' i y ≤ y', onda je x + y < x' + y' . Dokaze možete pronaći u [CT] i [DK]. Tek sada imamo sve što je potrebno za dokazivanje da je zbroj dvaju nadrealnih brojeva nadrealan broj! Zadatak 7. Ako su a i b nadrealni brojevi, tada je a + b nadrealan broj. Označimo s N skup nadrealnih brojeva. Teorem 10. (N, +) je komutativna grupa. Zapravo N nije skup nego prava klasa, kao što ćemo vidjeti u 5. cjelini, tako da termin grupa nije posve prikladan. Svojstva asocijativnosti i komutativnosti lako je dokazati, kao i to da je neutralni element 0. Postojanje inverznog elementa − x dokazuje se indukcijom. Nećemo se detaljno baviti množenjem već ćemo samo dati uvid u definiciju kako bismo se mogli bolje zabaviti u idućoj cjelini.
Prvo bismo, naravno, trebali dokazati da je umnožak dvaju nadrealnih brojeva nadrealan broj. Uz istu napomenu u vezi s N kao maloprije, vrijedi: Teorem 11. (N\{0}, ·) je komutativna grupa. Ako vas interesira množenje, više o tome možete naći u [JC], [CT] i [DK]. 5. Do beskonačnosti i daljeAko nastavimo stvarati brojeve kao u 2. cjelini, dobivat ćemo redom racionalne brojeve koji u nazivniku imaju potenciju broja 2. No, što je sa svim ostalim realnim brojevima, naprimjer s ⅓? Svi na ovaj način stvoreni brojevi imaju konačan zapis u binarnom obliku. S druge strane, svaki broj koji ima konačan zapis u binarnom obliku prije ili kasnije bit će stvoren. No, ⅓ nema konačan zapis: Znači, ⅓ ne može biti stvoren nakon konačno mnogo koraka. Takvi brojevi rođeni su na dan א kad nam na raspolaganju stoje svi brojevi s konačnim binarnim zapisom. Da bismo dobili ⅓, možemo uzeti (u binarnoj notaciji) XL = {0.01, 0.0101, 0.010101, 0.01010101,...} i XR = {0.1, 0.011, 0.01011, 0.0101011,...}. Na sličan način dolazimo do broja π. Neću vam uskratiti užitak! Zadatak 8. Nađite jedan mogući izbor lijevog skupa i desnog skupa broja π. Dakle, na dan א stvoreni su svi brojevi iz skupa realnih brojeva R. Nadrealni brojevi do sada nam nisu dali ništa novog... ili možda ipak jesu? Uzmimo XL = {0} i XR = {1, ½, ¼, ⅛, ...}. To je broj veći od 0 i manji od svih pozitivnih realnih brojeva! Možemo ga zvati ε. Ako stavimo XL = {1} i XR = {1½, 1¼, 1⅛, ...}, dobivamo broj x = {XL | XR} koji je "za dlaku" veći od 1. Sada je jasno da postoji broj "odmah do" svakog realnog broja, pa tako i do broja π. Međutim, on nastaje tek na dan א + 1, a na dan א samo brojevi s konačnim binarnim zapisom dobivaju beskonačno bliskog susjeda. Primijetimo da na dan א + 1 dobivamo i broj između 0 i ε. Na dan א stvoren je još jedan broj koji ne pripada skupu realnih brojeva: ω = {1, 2, 3, 4, 5,... | Ø}. Taj broj veći je od svih prirodnih brojeva, dakle i od svih realnih! Čitatelji upoznati s transfinitnim brojevima prepoznaju prvi beskonačni ordinal. Ordinalni brojevi zapravo su redni brojevi, odnosno proširenje pojma rednog broja na beskonačan slučaj. Možemo ih reprezentirati kao nadrealne brojeve kojima je desni skup prazan. Više o ordinalnim brojevima potražite npr. u [MV]. Primijetimo da se zbrajanje nadrealnih brojeva razlikuje od zbrajanja ordinala. Poznato je da zbrajanje ordinala općenito nije komutativno. Naprimjer, vrijedi 1 + ω = ω, ali je ω + 1 > ω. S druge strane, iz definicije zbrajanja nadrealnih brojeva imamo 1 + ω = ω + 1 = {ω, 2, 3, 4, 5,... | Ø}. To možemo pojednostavniti na {ω | Ø}.
Broj ω + ½
još je zanimljiviji, no jednako se lako pokazuje
da vrijedi ω + ½ ≡
{ω | ω + 1}. Možemo li izračunati
ω − 1? Nadam se da to niste pokušavali na Teoriji
skupova Možemo promatrati razne brojeve poput ω + ω = {ω + 1, ω + 2, ω + 3, ω + 4,... | Ø}, 3ω = {2ω + 1, 2ω + 2, 2ω + 3, 2ω + 4, ... | Ø} koji je stvoren na dan 3א, ω2 = {ω, 2ω, 3ω, 4ω,... | Ø} koji je stvoren na dan א2, ωω = {ω, ω2, ω3, ω4,... | Ø} (na koji dan je stvoren?) i još uvijek smo samo na početku... Što li se tek događa s "malim" brojevima na dane kada nastaju brojevi ωωω, ωωωω i tako dalje? Zadatak 9. Dokažite ε · ω ≡ 1. Zadatak 10. Dokažite √ω ≡ {1, 2, 3, 4,... | ω/1, ω/2, ω/3, ω/4, ...}. Iako nadrealni brojevi dopuštaju zbrajanje, množenje, potenciranje i logaritmiranje, problemi se javljaju kada dođemo do integriranja. Ironično, problemi nastaju upravo zbog veličine njihova kraljevstva. Bez integriranja, nadrealni brojevi nisu od interesa za fiziku pa dok (i ako) se ne uspije naći rješenje te teškoće, nadrealni brojevi čekaju svoj procvat. Ostalo je još beskonačno stvari za učiniti... i samo konačno mnogo vremena... [DK] Literatura
1. Uvod |

 xR,
odnosno kraće
XL
xR,
odnosno kraće
XL 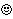 .
Sad se lako vidi (a i ima smisla!) da je
ω − 1 ≡
{1, 2, 3, 4,... | ω}
prvi broj veći od svih cijelih brojeva, ali manji od ω.
Broj ω + π ≡
{ω + ΠL | ω + ΠR}
stvoren je na dan 2א, zajedno s
ω + ε i
ω − ε.
.
Sad se lako vidi (a i ima smisla!) da je
ω − 1 ≡
{1, 2, 3, 4,... | ω}
prvi broj veći od svih cijelih brojeva, ali manji od ω.
Broj ω + π ≡
{ω + ΠL | ω + ΠR}
stvoren je na dan 2א, zajedno s
ω + ε i
ω − ε.