
Broj 6




















Matko Botinčan
Kombinatorne igre


Sadržaj:
1. Uvod2. Reprezentacija igara pomoću grafa, odnosno stabla
3. Ukratko o klasifikaciji igara
4. Formalna definicija igara
5. Operacije na igrama
6. Igre stupnja dva
7. Pojednostavljivanje igara
8. Imparcijalne igre
9. Još malo o Nimu i imparcijalnim igrama
Literatura
1. Uvod
U intrigantnom igranom filmu L’Année dernière à Marienbad (“Prošle godine u Marienbadu”) [1] osoba M nagovara osobu X da odigraju jednu jednostavnu igru. Osoba M posloži karte na stol na sljedeći način:

Igra koju u filmu igraju osobe M i X poznata je pod imenom Nim (dolazi od njemačke riječi nehmen) te je jedna od najstarijih i najpoznatijih matematičkih igara za dva igrača. Samo ime igre pod kojim je ona danas poznata kao i njezina precizna matematička teorija nastali su još početkom prošlog stoljeća pionirskim radom C. L. Boutona [2].
Općenito se igra, dakako, može igrati predmetima bilo koje vrste (sigurno ste barem jednom imali priliku susresti varijantu s npr. šibicama, kamenčićima, novčićima i sl.), a pravila za određivanje pobjednika znaju varirati. Naime, u standardnoj varijanti igre pobjeđuje igrač koji uzima posljednji predmet, a u tzv. mizernoj varijanti igrač koji odigra posljednji potez gubi. Igrači iz filma [1] igraju, dakle, mizernu varijantu Nima.
Neki od čitatelja sigurno već znaju zašto osoba X u opisanoj situaciji gubi igru. Naime, Nim je primjer igre koja ima svojstvo da sa svake njezine pozicije uvijek točno jedan igrač ima pobjedničku strategiju (za takve igre kažemo da su determinirane), a pripadna je strategija praktički jednostavno provedljiva. Pogledajmo ukratko o čemu je riječ (pretpostavivši pri tome da igramo standardnu varijantu Nima). Uvedimo pojam korektne pozicije u igri na sljedeći način. Izrazimo broj predmeta na svakoj hrpi u binarnom sustavu te dobivene brojeve potpišimo jedan ispod drugoga (kao kad npr. zbrajamo brojeve na papiru). Reći ćemo da je dana pozicija Nima korektna ako je zbroj brojeva u svakom od stupaca paran. U protivnom govorimo o inkorektnoj poziciji. Indukcijom nije teško pokazati da tada vrijedi:
Teorem 1: S dane pozicije u Nimu igru dobiva drugi igrač (onaj koji drugi vuče potez) ako i samo ako je pozicija korektna.
Zadatak 1: Provedite induktivni dokaz ove tvrdnje.
Uputa: Uočite kako svaki
potez odigran s korektne pozicije nužno rezultira inkorektnom pozicijom, a
sa svake inkorektne pozicije moguće je odigrati potez na korektnu poziciju.
- ako je početna pozicija u igri inkorektna, igrač koji je prvi na potezu ima pobjedničku strategiju;
- ako je početna pozicija u igri korektna, igrač koji je drugi na potezu ima pobjedničku strategiju.
Zadatak 2: I za mizernu varijantu Nima postoji slična karakterizacija koja određuje s kojih pozicija pobjeđuje prvi, a s kojih drugi igrač. Pronađite tu karakterizaciju te odredite kako u tom slučaju izgledaju pobjedničke strategije za igrače.
Opisana karakterizacija u potpunosti rješava pitanje pobjednika u igri Nim te pobjedničkom igraču nalaže kako treba optimalno igrati da bi dobio igru. Pitanja o nalaženju pobjednika i pobjedničkih strategija prirodno se nameću praktički kod svih tipova igara, no također je interesantno zapitati se u kojim bismo sve igrama mogli upotrijebiti pobjedničku strategiju analognu onoj iz igre Nim. Osnovni cilj ovog teksta jest prezentirati jedan od temeljnih odgovora na ovo drugo pitanje. Također, namjera nam je pri tome upoznati čitatelja i s osnovnim konceptima koji figuriraju u kombinatornoj teoriji igara te posebno mlađim čitateljima dočarati na koji način u ovom konkretnom slučaju snaga i elegancija matematičke apstrakcije dolaze do izražaja.2. Reprezentacija igara pomoću grafa, odnosno stabla
Način na koji se odvija igra često je korisno prikazati pomoću usmjerenog grafa, u kojem njegovi vrhovi predstavljaju moguće pozicije u igri, a bridovi moguće opcije svakog od igrača. Primjerice, igra Nim s jednom hrpom od jednog i još jednom hrpom od triju predmeta reprezentirana usmjerenim grafom izgledala bi ovako:
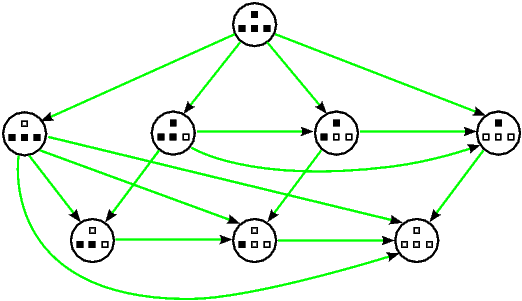
Primijetimo: da bismo uopće mogli primijeniti opisani kriterij određivanja pobjednika u igri, moramo biti sigurni da igra završava nakon konačnog broja koraka, tj. da nijednim izborom poteza ne može nastati beskonačni niz pozicija (uočite kako će to biti slučaj ako u pripadnom grafu igre ne postoji beskonačno dugački put). Tipične matematičke igre poput Nima imaju to svojstvo, no to ne mora uvijek biti tako — uzmite za primjer igru šah (prisjetite se na koji se način u šahu rješavaju takve situacije u igri; naime, nijedna stvarna partija šaha ipak ne traje beskonačno dugo). Tretiranje beskonačnih tijekova igre općenito nije jednostavno i takvim se igrama nećemo baviti u ovom tekstu.
Često je zgodno prikazati sve moguće tijekove igre (sve različite puteve u reprezentaciji igre usmjerenim grafom) pomoću stabla. Kako bi to izgledalo za prethodni primjer igre Nim s hrpama od jednog i triju predmeta, možete vidjeti na idućoj slici:
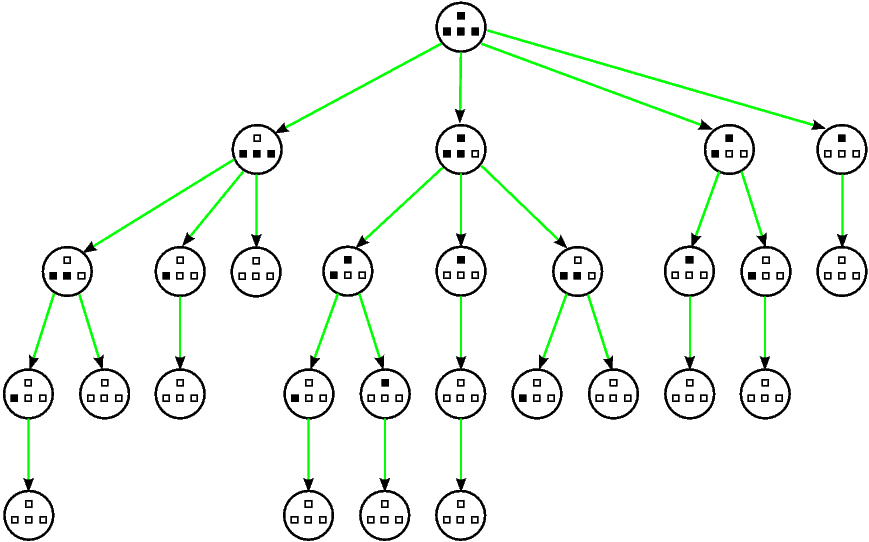
Na kraju ove točke istaknimo još jednom ključne pojmove koji će nam biti važni u daljnjem tekstu:
- igra — usmjereni graf ili stablo koji reprezentiraju pravila igre;
- pozicije u igri — vrhovi usmjerenog grafa, odnosno stabla;
- opcije igrača — bridovi usmjerenog grafa, odnosno stabla.
3. Ukratko o klasifikaciji igara
Čitatelji hrvatskog matematičkog elektronskog časopisa math.e sigurno se sjećaju članka Vedrana Krčadinca iz trećeg broja časopisa, koji je govorio o teoriji igara i matematičkom modeliranju konfliktnih situacija [3]. Igra Nim, kao i one koje ćemo razmatrati dalje u ovom tekstu, drugačije su od igara opisanih u navedenom članku. Kako bismo raščistili eventualno moguću zabunu o korištenoj terminologiji, napravit ćemo kratku digresiju o općenitoj klasifikaciji igara u teoriji igara.Teorija igara velika je znanstvena disciplina koja svoje korijene vuče ponajviše iz matematike i ekonomije. U najširem smislu podijeljena je u dvije grane:
- Kooperativna teorija igara — proučava igre sljedećih svojstava:
- pravila igre su neprecizno (i često samo implicitno) opisana;
- individualne probleme odluke pojedinih igrača u pravilu je nemoguće direktno analizirati pa se stoga stavlja naglasak na proučavanje koalicija igrača;
- s obzirom da postoji pretpostavka o mogućnosti formiranja i održavanja koalicija, moguće je i stvaranje kompromisa.
- Nekooperativna teorija igara — proučava igre sljedećih svojstava:
- pravila igre precizno su definirana i potpuna;
- temeljne jedinice odluke su individualni igrači;
- nije moguće stvaranje kompromisa (osim u slučaju kada pravila igre to eksplicitno dopuštaju).
Igre kojima ćemo se baviti u ovom tekstu spadaju, dakako, u nekooperativnu teoriju igara. Iako one, zbog svoje nekooperativnosti, predstavljaju već znatnu simplifikaciju realnih situacija, vidjet ćemo da su još uvijek sve prije negoli jednostavne. Općenito, igre takvog tipa ne završavaju nužno samo pobjedom ili porazom, već uključuju niz mogućih ishoda zajedno s pripadnim preferencijama svakog od igrača. Pri tome očekivani dobitak u igri utječe na ponašanje igrača. Osnovni cilj jest predvidjeti racionalno ponašanje igrača u raznim konfliktnim situacijama te objasniti pod kojim uvjetima dolazi do “stabiliziranja”.
Da bismo jasnije odredili kakvi nas to točno tipovi nekooperativnih igara zanimaju, moramo napraviti određenu distinkciju među njima. Uzmimo kao primjer igru Nim i neku tipičnu kartašku igru, npr. Briškulu. Ako malo razmislimo, uočit ćemo da postoje dvije ključne razlike između igara poput Nima i igara poput Briškule:
- U igri Nim, trenutno stanje igre uvijek je vidljivo obojici igrača; kažemo da igrači imaju potpunu informaciju. Jedina nepoznanica u igri su potezi koji će biti odigrani u budućnosti. U Briškuli, s druge strane, igrači imaju nepotpunu informaciju, odnosno imaju samo parcijalni uvid u stanje igre (svaki igrač vidi samo svoje karte).
- Nim je igra bez elemenata slučajnosti (svi elementi igre deterministički su određeni), a kod Briškule to nije tako (ne znamo unaprijed koje ćemo karte dobiti prilikom dijeljenja). Za Briškulu kažemo da je igra s elementima slučajnosti.
Uočimo kako u igrama nepotpune informacije postoji neizvjesnost o trenutnom stanju igre (odnosno, o sadašnjosti). S druge pak strane, igre s elementima slučajnosti uključuju samo neizvjesnost o budućnosti (pri tome neizvjesnost budućeg poteza nestaje čim taj potez bude odigran).
Dakle, sve skupa zaključujemo kako nekooperativne igre ima smisla podijeliti na one potpune, odnosno nepotpune informacije, te na one sa, odnosno bez elemenata slučajnosti. Na taj je način svaku nekooperativnu igru moguće svrstati u jednu od četiriju dobivenih skupina. Klasifikacija nekolicine popularnih igara prikazana je u sljedećoj tablici:
| igre potpune informacije | igre nepotpune informacije | |
| bez elemenata slučajnosti | Nim, Šah, Go | Potapanje brodova |
| s elementima slučajnosti | Monopoly, “Čovječe ne ljuti se” | Briškula, Bela, Poker |
Teorija igara u ekonomiji fokusirana je na donošenje odluka pod utjecajem neizvjesnosti, dakle, bilo na igre nepotpune informacije, bilo na one s elementima slučajnosti. Kada se u užem smislu govori o teoriji igara, misli se upravo na takve igre. Sada je sigurno već jasno da nam je Vedran Krčadinac u članku [3] pisao upravo o takvim tipovima igara.
S druge strane, mi se u ovom tekstu bavimo igrama koje se nalaze u onoj “preostaloj” kategoriji, tj. (ne-kooperativnim) igrama potpune informacije bez elemenata slučajnosti. Takve su igre prvenstveno od matematičkog interesa (makar to ne znači da nemaju primjenu i u drugim područjima; sjetite se, primjerice, uvodnog dijela ovog teksta), a kako tipično imaju dodirnih točaka s kombinatorikom i teorijom grafova, teorija koja se oko njih razvila naziva se kombinatornom teorijom igara. Ovime smo također dali i svojevrsno opravdanje zašto smo u naslovu upotrijebili termin kombinatorne igre.
4. Formalna definicija igara
Igre potpune informacije bez elemenata slučajnosti, koje krećemo analizirati igraju samo dva igrača. Radi jednostavnosti igrače kratko nazivamo lijevim (L), odnosno desnim (D) (namjerno ne koristimo nazive “prvi”, odnosno “drugi” igrač, kako ne bi došlo do zabune kad budemo govorili o igraču koji je prvi, odnosno drugi na potezu). Dakle, budući da za svaku poziciju u igri pravila igre jednoznačno određuju dva skupa opcija koje su dostupne pojedinom igraču, igru možemo (naizgled možda jako jednostavno) definirati kao uređeni par skupova igara. Ako igru označimo s G, tada definicija kaže da je
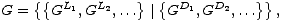
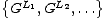 , odnosno
, odnosno
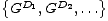 ,
skupovi opcija lijevog, odnosno
desnog igrača. Bazu ove induktivne definicije predstavlja igra u kojoj nijedan od
igrača nema što odigrati, tj. igra oblika:
,
skupovi opcija lijevog, odnosno
desnog igrača. Bazu ove induktivne definicije predstavlja igra u kojoj nijedan od
igrača nema što odigrati, tj. igra oblika:
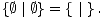
 ,
pri čemu onda GL, odnosno
GD,
predstavljaju skupove opcija igrača L, odnosno D.
,
pri čemu onda GL, odnosno
GD,
predstavljaju skupove opcija igrača L, odnosno D.
Napomenimo i to da igru 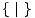 nismo slučajno označili s 0.
Od ovog trenutka
nadalje pojedine igre svjesno ćemo označivati simbolima za brojeve jer ćemo
takvim igrama moći manipulirati na način sličan onom kojim manipuliramo
brojevima u standardnoj aritmetici. Da bismo tu ideju razjasnili i preciznije opisali,
promotrimo prethodno nekoliko jednostavnih primjera.
nismo slučajno označili s 0.
Od ovog trenutka
nadalje pojedine igre svjesno ćemo označivati simbolima za brojeve jer ćemo
takvim igrama moći manipulirati na način sličan onom kojim manipuliramo
brojevima u standardnoj aritmetici. Da bismo tu ideju razjasnili i preciznije opisali,
promotrimo prethodno nekoliko jednostavnih primjera.
Svakoj igri korisno je dodijeliti stupanj koji opisuje njezinu jednostavnost. Nakon
svakog odigranog poteza igra postaje jednostavnija u smislu da stižemo u poziciju
igre manjeg stupnja. Najjednostavnija igra (i jedina stupnja 0) jest igra 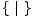 s
praznim skupom opcija za lijevog i desnog igrača. U idućem koraku kao opcije
imamo na raspolaganju Ø i 0 =
s
praznim skupom opcija za lijevog i desnog igrača. U idućem koraku kao opcije
imamo na raspolaganju Ø i 0 = 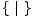 pa tako igara stupnja 1
ima ukupno četiri (= 2 . 2) i
to su: 0, 1 =
pa tako igara stupnja 1
ima ukupno četiri (= 2 . 2) i
to su: 0, 1 = 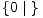 , -1 =
, -1 = 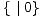 , te * =
, te * = 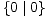 . Pripadajuća stabla ovih igara
prikazana su na sljedećoj slici (pri tome opcije igrača L bojimo plavom bojom, a
opcije igrača D crvenom):
. Pripadajuća stabla ovih igara
prikazana su na sljedećoj slici (pri tome opcije igrača L bojimo plavom bojom, a
opcije igrača D crvenom):
 |  |  |  |
0 = 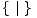 | 1 = 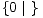 | -1 = 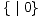 | * = 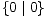 |
Prikazane igre predstavljaju prototipove igara s obzirom na koje ćemo klasificirati sve složenije igre. One imaju sljedeća ključna svojstva:
- Igra 0 prototip je igre u kojoj gubi igrač koji je prvi na potezu (jer nema što odabrati), odnosno drugi igrač pobjeđuje. Za takve igre kažemo da imaju vrijednost 0.
- U igri 1, pak, uvijek pobjeđuje lijevi igrač bez obzira na to koji igrač igra prvi potez. Sve igre takvog tipa imaju pozitivnu vrijednost.
- Analogno, u igri -1, uvijek pobjeđuje desni igrač. Sve igre takvog tipa imaju negativnu vrijednost.
- U igri * =
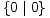 pobjeđuje onaj igrač
koji je prvi na potezu i ona predstavlja najjednostavniju igru koja nije broj.
Za igre takvog tipa kae se da su neizrazite (engl. fuzzy) jer njihova vrijednost nije ni
0 ni pozitivna ni negativna.
pobjeđuje onaj igrač
koji je prvi na potezu i ona predstavlja najjednostavniju igru koja nije broj.
Za igre takvog tipa kae se da su neizrazite (engl. fuzzy) jer njihova vrijednost nije ni
0 ni pozitivna ni negativna.
Dakle, svaku igru možemo prema ishodu svrstati u jednu od navedenih četiriju klasa, kako je to sistematizirano sljedećom tablicom:
| počinje
D i
| |||
| Ako u igri
G | L ima pobjedničku | D ima pobjedničku | |
| strategiju | strategiju | ||
počinje L i | D ima pobjedničku | G = 0 | G < 0 |
| strategiju | (drugi pobjeđuje) | (D pobjeđuje) | |
| L ima pobjedničku | G > 0 | G || 0 | |
| strategiju | (L pobjeđuje) | (prvi pobjeđuje) | |
Uočimo i to kako relacija G = 0 u ovoj tablici ne govori da je sama igra G jednaka igri 0 (nula), već da je riječ o igri kojoj je vrijednost jednaka 0, tj. da igra G pripada klasi igara u kojoj drugi igrač ima pobjedničku strategiju. Isto tako, relacija G || 0 označuje da je igra G neusporediva s igrom 0, tj. da je riječ o igri u kojoj pobjedničku strategiju ima prvi igrač.
5. Operacije na igrama
Zamislite da ste u situaciji u kojoj igrate vašu omiljenu igru protiv izvrsnog protivnika, kojeg nikako ne uspijevate pobijediti. Sigurno biste u takvoj situaciji voljeli imati mogućnost da, nakon što jednom ustanovite kako je vaša šansa za pobjedu u igri postala gotovo zanemariva, prepustite svoje mjesto vašem protivniku, a vi preuzmete njegovu ulogu. Iako ovakav tip operacije nije baš uobičajen u igrama iz svakodnevnog života, on je ipak poželjan i koristan u matematičkim igrama. Operacija koja igru G zamjenjuje njoj suprotnom igrom -G definirana je induktivno ovako:
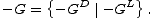
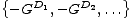 ,
gdje svaka pojedina opcija predstavlja igru jednostavniju od -G.
,
gdje svaka pojedina opcija predstavlja igru jednostavniju od -G.
Nadalje, na igrama možemo definirati i operaciju sume. Naprimjer, svaka igra Nim suma je određenog broja igara Nim s jednom hrpom. U danoj sumi igrač koji je na potezu bira jednu od komponenata sume te u njoj odigrava jedan od mogućih poteza. Stoga definicija sume igara G i H izgleda ovako:
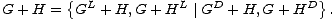
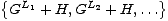 , svaka od kojih je igra jednostavnija od
G + H.
, svaka od kojih je igra jednostavnija od
G + H.
Nije teško provjeriti da na ovaj način definirana suma ima svojstvo komutativnosti
(G + H = H + G) i asocijativnosti
(F + (G + H) =
(F + G) + H) te da vrijedi
G + 0 = G i G + (-G) = 0
(drugim riječima, igre sa sumom kao binarnom operacijom
uvjetno rečeno čine grupu). Pri tome treba biti malo oprezan s čitanjem
posljednjih dviju relacija jer je simbol 0 u njima upotrijebljen u dva bitno
različita smisla. U relaciji G + 0 = G simbol 0 predstavlja igru nula, odnosno
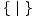 . S druge strane, relacija
G + (-G) = 0 govori da je igra G + (-G) igra
vrijednosti 0, odnosno da pripada klasi igara u kojoj drugi igrač ima pobjedničku
strategiju.
. S druge strane, relacija
G + (-G) = 0 govori da je igra G + (-G) igra
vrijednosti 0, odnosno da pripada klasi igara u kojoj drugi igrač ima pobjedničku
strategiju.
Zadatak 3: Provjerite da vrijede sljedeće jednakosti:
- 1 + (-1) = 0 (u igri 1 + (-1) pobjeđuje drugi igrač);
- * + * = 0 ( u igri * + * pobjeđuje drugi igrač).
Sada možemo definirati relaciju ekvivalencije na igrama na način da za igre G i H kažemo da su ekvivalentne, u oznaci G = H, ako u igri G + (-H) pobjeđuje drugi igrač, odnosno vrijedi G + (-H) = 0. Štoviše, na igrama možemo definirati i parcijalni uređaj >, pri čemu G > H označuje da je G + (-H) > 0, tj. u igri G + (-H) uvijek pobjeđuje igrač L, neovisno o tome koji igrač započinje igru.
Zadatak 4: Pokušajte dokazati sljedeće tvrdnje:
- Ako je G ≥ 0 i H ≥ 0, tada je i G + H ≥ 0. (Napomena: G ≥ 0 označuje G = 0 ili G > 0)
- Ako je H = 0, tada igra G + H ima isti ishod kao i igra G.
6. Igre stupnja dva
Vidjeli smo da igara stupnja jedan imamo ukupno četiri pa iz njih dobivamo ukupno 24 = 16 mogućih opcija za svakog od igrača L i D, što sve skupa daje 256 igara stupnja dva. Ipak, efektivni broj različitih igara stupnja dva možemo bitno reducirati ako uočimo da neke opcije igrači očito preferiraju u odnosu na druge. Naime, četiri igre stupnja jedan nalaze se u odnosu koji možemo ilustrirati ovakvim dijagramom:
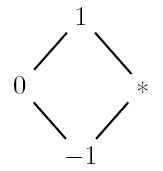
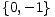 igrač L očito će preferirati
0, a u skupu
igrač L očito će preferirati
0, a u skupu 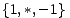 igrač D preferirat će opciju
-1. Jedini skup opcija u kojem
nije a priori jasno što bi bila najbolja opcija za pojedinog igrača jest skup
igrač D preferirat će opciju
-1. Jedini skup opcija u kojem
nije a priori jasno što bi bila najbolja opcija za pojedinog igrača jest skup 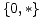 .
Stoga je za opcije igrača u igrama stupnja dva potrebno uzeti u obzir jedino sljedeće
skupove: Ø, -1, *, 0,
.
Stoga je za opcije igrača u igrama stupnja dva potrebno uzeti u obzir jedino sljedeće
skupove: Ø, -1, *, 0, 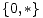 i 1. Između 62
= 36 rezultantnih igara stupnja dva samo su 22 međusobno neekvivalentne (pri tome su četiri od njih ekvivalentne već
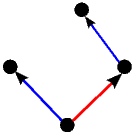
poznatim igrama stupnja jedan). Pripadna stabla tih igara prikazuje sljedeća
slika.
i 1. Između 62
= 36 rezultantnih igara stupnja dva samo su 22 međusobno neekvivalentne (pri tome su četiri od njih ekvivalentne već
poznatim igrama stupnja jedan). Pripadna stabla tih igara prikazuje sljedeća
slika.
 |  |  |  |  |
| 0 | 1 | -1 | 2 | -2 |
 |  | 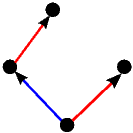 |  | 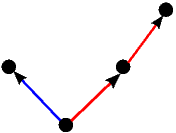 |
| * | 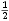 | -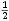 |  | 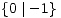 |
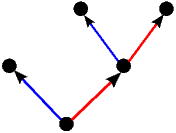 | 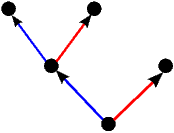 |  |  |  |
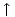 |  | 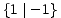 = ±1 = ±1 | 1* | -1* |
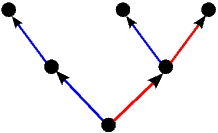 | 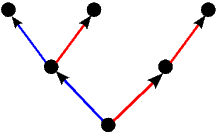 |  |  | |
 | 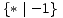 | 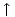 * * | 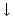 * * | |
 |  |  | ||
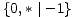 | 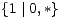 | *2 | ||
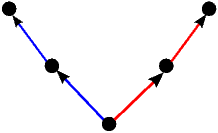
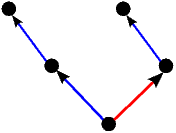
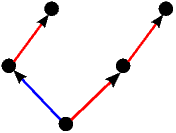
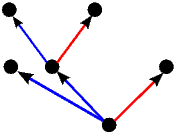
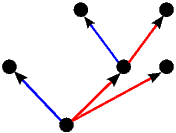
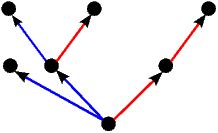
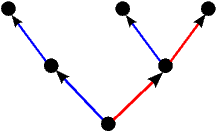
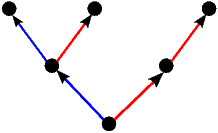
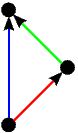
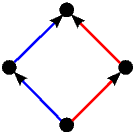
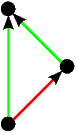
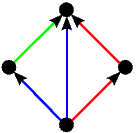
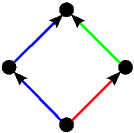
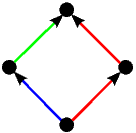
Kao što smo vidjeli u uvodnom dijelu ovog teksta na primjeru igre Nim, svaku igru možemo prikazati bilo kao stablo, bilo kompaktnije u obliku usmjerenog grafa. Stabla prvih 5 igara s prethodne slike predstavljaju istovremeno i njihove grafove pa stoga na sljedećoj slici dajemo ilustraciju grafova za preostalih 17 igara. Opcije igrača L, odnosno D, i dalje su obojene plavo, odnosno crveno, dok su zajedničke opcije obaju igrača obojene zelenom bojom.
 | 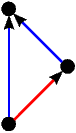 | 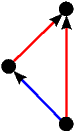 | 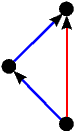 | 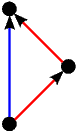 |
| * | 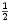 | -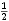 | 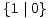 | 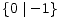 |
 |  |  |  |  |
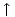 | 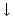 | ±1 | 1* | -1* |
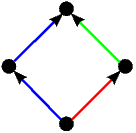 | 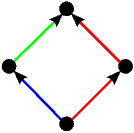 |  |  | |
 | 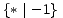 | 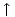 * * | 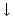 * * | |
 |  |  | ||
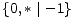 | 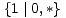 | *2 | ||
Među dane 22 igre imamo jednu igru vrijednosti nula, šest negativnih, šest pozitivnih, te devet neizrazitih igara. Vrijednosti ishoda svih igara sistematizirane su u sljedećoj tablici. Pri tome igra vrijednosti nula nalazi se u gornjem lijevom, negativne igre u gornjem desnom, pozitivne u donjem lijevom, a neizrazite u donjem desnom kvadrantu.
| Ø | 1 | * | 0 | 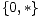 | -1 | |
| Ø | -1 | -2 | ||||
| -1 | 0 | 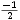 | -1* | |||
| * | 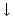 | 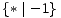 |
||||
| 0 |
1 | 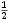 | 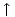 | * | 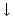 * * | 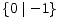 |
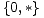 | 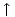 * * | *2 | 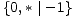 |
|||
| 1 | 2 | 1* | 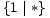 | 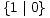 | 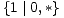 | ±1 |
Zadatak 5: Dokažite da vrijede sljedeće tvrdnje:
- 1 + 1 = 2;
-
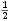 +
+ 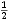 = 1;
= 1;
-
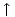 =
= 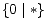 =
=  ≥ 0;
≥ 0;
-
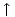 * =
* = 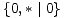 =
= 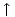 + *;
+ *;
- 0 ||* 2 =
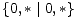 ;
;
- 1* =
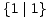 = 1 + *;
= 1 + *;
-
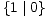 > *;
> *;
-
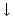 * =
* = 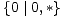 || 0;
|| 0;
-
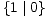 >
> 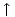 *,
*, 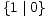 > *2,
> *2,
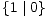 >
> 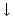 = *| 0,
= *| 0, 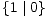 >
> 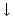 *,
*, 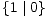 > ±1 =
> ±1 = 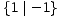 ,
, 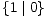 || 0,
|| 0, 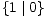 ||
|| 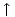 ;
;
-
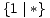 > 0,
> 0, 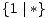 >
> 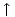 ,
, 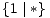 ||
|| 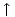 *;
*;
-
 >
> 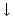 ,
, 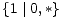 ||
|| 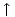 .
.
7. Pojednostavljivanje igara
Prisjetimo se da smo prilikom nalaženja svih međusobno neekvivalentnih igara stupnja dva zbog očitih preferencija pojedinih opcija naspram drugih smjeli izbaciti one manje “poželjne” opcije pojedinog igrača. Općenito, ako u igri G = vrijedi
GL
vrijedi
GL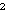 ≥
GL
≥
GL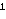 ,
kažemo da
GL
,
kažemo da
GL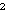 dominira
GL
dominira
GL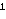 te u tom slučaju smijemo izbaciti opciju
GL
te u tom slučaju smijemo izbaciti opciju
GL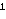 (pod uvjetom da
GL
(pod uvjetom da
GL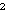 bude zadržana). Kod desnog igrača situacija je suprotna — kažemo da
GD
bude zadržana). Kod desnog igrača situacija je suprotna — kažemo da
GD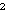 dominira
GD
dominira
GD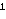 ako vrijedi
GD
ako vrijedi
GD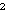 ≤
GD
≤
GD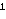 te opet smijemo izbaciti opciju
GD
te opet smijemo izbaciti opciju
GD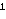 (ako zadržimo GD
(ako zadržimo GD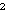 ).
Brisanje dominiranih opcija jedan je način za pojednostavljivanje
igara.
).
Brisanje dominiranih opcija jedan je način za pojednostavljivanje
igara.
Drugi, nešto suptilniji način, sastoji se od zamjene tzv. reverzibilnih
opcija. Opciju desnog igrača X nazivamo reverzibilnom ako lijevi igrač
ima odgovor XL, koji je za njega barem jednako toliko dobar koliko i dana
igra G, tj. ako vrijedi
XL
≥ G. U tom slučaju X smijemo zamijeniti
nizom svih desnih opcija XLD = 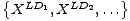 od XL. Slično, opcija
lijevog igrača Y je reverzibilna ako desni igrač ima odgovor
YD,
koji je
za njega barem jednako toliko dobar koliko i sama igra G, tj. ako je
YD ≤ G
te tada Y smije biti zamijenjen nizom svih lijevih opcija
YDL
od YD.
od XL. Slično, opcija
lijevog igrača Y je reverzibilna ako desni igrač ima odgovor
YD,
koji je
za njega barem jednako toliko dobar koliko i sama igra G, tj. ako je
YD ≤ G
te tada Y smije biti zamijenjen nizom svih lijevih opcija
YDL
od YD.
Primjerice, u igri G = 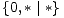 nijedna opcija lijevog igrača ne dominira
nad onom
drugom budući da je 0 ||*, ali je zato njegova opcija * reverzibilna, budući da je pripadni
odgovor desnog igrača *R = 0, a za igru G vrijedi
G ≥ 0 (uvjerite se da je to doista
tako!). To znači da opciju lijevog igrača * možemo zamijeniti svim opcijama
lijevog igrača od *R
= 0 =
nijedna opcija lijevog igrača ne dominira
nad onom
drugom budući da je 0 ||*, ali je zato njegova opcija * reverzibilna, budući da je pripadni
odgovor desnog igrača *R = 0, a za igru G vrijedi
G ≥ 0 (uvjerite se da je to doista
tako!). To znači da opciju lijevog igrača * možemo zamijeniti svim opcijama
lijevog igrača od *R
= 0 = 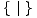 , tj. možemo je zamijeniti svim opcijama praznog
skupa, dakle, možemo je obrisati. Na taj se način polazna igra G pojednostavljuje u
igru
, tj. možemo je zamijeniti svim opcijama praznog
skupa, dakle, možemo je obrisati. Na taj se način polazna igra G pojednostavljuje u
igru 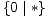 =
= 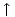 .
.
Zadatak 6: Analizirajte reverzibilne opcije u igri 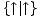 , te je pojednostavite.
, te je pojednostavite.
8. Imparcijalne igre
Imparcijalnom igrom nazivamo onu igru kod koje je skup opcija lijevog igrača jednak skupu opcija desnog igrača. Imparcijalne igre koje smo susreli u prethodnim točkama bile su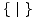 = *0 = 0,
= *0 = 0, 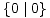 = *1 = *, te
= *1 = *, te 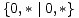 = *2. Ovu
konstrukciju nije teško generalizirati pa na taj način kao igru stupnja n dobivamo
igru sljedećeg oblika:
= *2. Ovu
konstrukciju nije teško generalizirati pa na taj način kao igru stupnja n dobivamo
igru sljedećeg oblika:
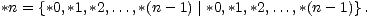
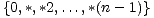 .
.
Zadatak 7: Zapišite pomoću nimbera općenitu igru Nim kod koje se u prvoj hrpi nalazi n1 predmeta, u drugoj hrpi n2 predmeta ..., te u k-toj hrpi nk predmeta.
Nadalje, uloga nimbera postaje još važnija ako uvidimo da vrijedi sljedeća tvrdnja: svaka igra oblika
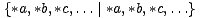
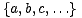 .
Da bismo to uvidjeli, potrebno je samo uočiti kako je svaka
opcija *n za n > m reverzibilna — naime, opcija *m od
*n ima svojstvo da
je ≥ *m — pa stoga *n možemo zamijeniti opcijama od
*m, odnosno s
0, *, *2, ..., *(m - 1).
.
Da bismo to uvidjeli, potrebno je samo uočiti kako je svaka
opcija *n za n > m reverzibilna — naime, opcija *m od
*n ima svojstvo da
je ≥ *m — pa stoga *n možemo zamijeniti opcijama od
*m, odnosno s
0, *, *2, ..., *(m - 1).
Dana argumentacija zapravo predstavlja induktivni korak dokaza činjenice da je svaka imparcijalna igra ekvivalentna nekom nimberu. Ova tvrdnja, koju su po prvi puta dokazali Sprague (1935.-36.) i Grundy (1939.), jedna je od prvih i temeljnih rezultata kombinatorne teorije igara.
Teorem 2 (Sprague-Grundy): Za svaku imparcijalnu igru G postoji m takav da vrijedi G = *m.
Zadatak 8: Napravite za vježbu kompletni induktivni dokaz Sprague-Grundyjevog teorema (bazu, pretpostavku, te korak indukcije).
9. Još malo o Nimu i imparcijalnim igrama
Postavlja se još pitanje kako odrediti pobjednika u danoj imparcijalnoj igri. Zbog Sprague-Grundyjevog teorema to je sada moguće (barem u teoriji) jer znamo odrediti pobjednika u svakoj instanci igre Nim. Ipak, igra je tipično predstavljena u obliku sume nimbera, pa bi bilo korisno znati kako se nimberi mogu efektivno sumirati.Znamo da vrijedi *n + 0 = *n, a nije teško pokazati da vrijedi i *n + *n = 0 (naime, opcije lijevog i desnog igrača su jednake). Krenimo izračunati koliko je *2 + *:
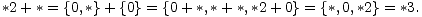
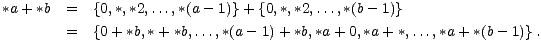
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 1 | 1 | 0 | 3 | 2 | 5 | 4 | 7 | 6 | 9 | 8 | 11 | 10 | 13 | 12 | 15 | 14 |
| 2 | 2 | 3 | 0 | 1 | 6 | 7 | 4 | 5 | 10 | 11 | 8 | 9 | 14 | 15 | 12 | 13 |
| 3 | 3 | 2 | 1 | 0 | 7 | 6 | 5 | 4 | 11 | 10 | 9 | 8 | 15 | 14 | 13 | 12 |
| 4 | 4 | 5 | 6 | 7 | 0 | 1 | 2 | 3 | 12 | 13 | 14 | 15 | 8 | 9 | 10 | 11 |
| 5 | 5 | 4 | 7 | 6 | 1 | 0 | 3 | 2 | 13 | 12 | 15 | 14 | 9 | 8 | 11 | 10 |
| 6 | 6 | 7 | 4 | 5 | 2 | 3 | 0 | 1 | 14 | 15 | 12 | 13 | 10 | 11 | 8 | 9 |
| 7 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 |
| 8 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 9 | 9 | 8 | 11 | 10 | 13 | 12 | 15 | 14 | 1 | 0 | 3 | 2 | 5 | 4 | 7 | 6 |
| 10 | 10 | 11 | 8 | 9 | 14 | 15 | 12 | 13 | 2 | 3 | 0 | 1 | 6 | 7 | 4 | 5 |
| 11 | 11 | 10 | 9 | 8 | 15 | 14 | 13 | 12 | 3 | 2 | 1 | 0 | 7 | 6 | 5 | 4 |
| 12 | 12 | 13 | 14 | 15 | 8 | 9 | 10 | 11 | 4 | 5 | 6 | 7 | 0 | 1 | 2 | 3 |
| 13 | 13 | 12 | 15 | 14 | 9 | 8 | 11 | 10 | 5 | 4 | 7 | 6 | 1 | 0 | 3 | 2 |
| 14 | 14 | 15 | 12 | 13 | 10 | 11 | 8 | 9 | 6 | 7 | 4 | 5 | 2 | 3 | 0 | 1 |
| 15 | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
Opcije pojedinog elementa u tablici čine sve ranije vrijednosti u istom retku i istom stupcu. Uočimo kako je svaki element tablice najmanji nenegativan cijeli broj koji se ne pojavljuje ranije u istom retku ili stupcu. Primjerice, *5 + *6 = *3 jer je 3 prvi broj koji se ne nalazi u skupu
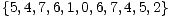 , odnosno
među prvih šest zapisa u petom retku i prvih pet zapisa u šestom stupcu tablice.
, odnosno
među prvih šest zapisa u petom retku i prvih pet zapisa u šestom stupcu tablice.
Ako malo bolje promotrimo relaciju *5 + *6 = *3, uvidjet ćemo da je nim-vrijednost 3 dobivena zbrajanjem bez prijenosa u bazi 2, odnosno logičkom operacijom eksluzivno ili (XOR) nim-vrijednosti 5 i 6. Ako tu operaciju nazovemo nim-sumiranjem, dobivamo:
Korolar 1: Nim-vrijednost sume dviju imparcijalnih igrara je nim-suma njihovih nim-vrijednosti.
Sada, dakle, imamo efektivan način za određivanje vrijednosti imparcijalnih igara.
Na kraju, zaključimo što možemo reći o ishodima u imparcijalnim igrama.
Korolar 2:
Svaka pozicija u imparcijalnoj igri je:
Ovakva karakterizacija, iskazana doduše nešto drugačijim riječima, bila je navedena za igru Nim još na samom početku ovog teksta. No, sada vidimo kako ista karakterizacija vrijedi i u znatno općenitijem kontekstu — sve imparcijalne igre imaju takvo svojstvo. To nam zapravo govori kako igra Nim upravo predstavlja prototip svih imparcijalnih igara pa je stoga njezina matematička, a i ona nematematička popularnost doista i teorijski opravdana. Ne znamo da li je te činjenice bio svjestan Alain Resnais, redatelj filma [1], no, očito, opredijelivši se u svom filmu za igru Nim, nije pogriješio.
Literatura
[1] A. Resnais. L’Année dernière à Marienbad. http://www.imdb.com/title/tt0054632/
[2] C. L. Bouton. Nim, a game with a complete mathematical theory. Annals of Mathematics 3 (1901-02), 35–39.
[3] V. Krčadinac. Teorija igara - matematičko modeliranje konfliktnih situacija. Math.e 3. http://www.math.hr/~mathe/teorijaigara/index.html
[4] E. R. Berlekamp, J. H. Conway and R. Guy. Winning ways for your Mathematical Plays. Academic Press, 1982.
[5] J. H. Conway. On Numbers and Games. Academic Press, 1976.
[6] R. Guy. Combinatorial Games. In Handbook of Combinatorics, R. Graham, M. Grotschel and L. Lovasz (Eds.), Vol. II, North-Holland, Amsterdam, 1996, 2117–2162.
1. Uvod
2. Reprezentacija igara pomoću grafa, odnosno stabla
3. Ukratko o klasifikaciji igara
4. Formalna definicija igara
5. Operacije na igrama
6. Igre stupnja dva
7. Pojednostavljivanje igara
8. Imparcijalne igre
9. Još malo o Nimu i imparcijalnim igrama
Literatura