Broj 2



















Vlatka Antončić, Andro Galinović
Galerija fraktala

Sadržaj:
UvodJuliaov skup
Mandelbrotov skup
Cantorova prašina i gredice
Igra kaosa
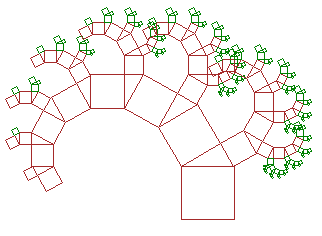
Pitagorino stablo
Kochova krivulja i pahuljica
Sierpinskijev trokut
Program i rad s programom
Implementacija programa
Literatura
Uvod
Program interaktivno (korak po korak) prikazuje nastanak Sierpinskijevog trokuta, Kochove pahuljice, Pitagorinog stabla, Cantorovih gredica te ostalih fraktala. Također, program omogućuje spremanje slika fraktala u različitim formatima (npr. gif, jpg, png).
Sve slike u ovom dokumentu generirane su pomoću gore navedenog programa.
Pojam fraktala uveo je Benoit Mandelbrot 1970. godine. Fraktal ima svojstvo da svaki njegov dio sadrži istu strukturu kao i cijeli objekt, tj. uvećana slika dijela fraktala između bilo koje dvije točke bit će identična izgledu samog fraktala.
Juliaov skup
Neka je C skup kompleksnih brojeva.
Za zadanu funkciju f :
C 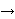 C , f n označava n-terostruku kompoziciju (f o f o ... o f).
Za z
C , f n označava n-terostruku kompoziciju (f o f o ... o f).
Za z 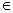 C gledamo niz kompleksnih brojeva
z1 = f(z0),
z2 = f 2(z0) =
f(z1), z3 = f 3(z0) = f(z2), ... .
Taj niz zovemo orbita nelinearnog procesa
C gledamo niz kompleksnih brojeva
z1 = f(z0),
z2 = f 2(z0) =
f(z1), z3 = f 3(z0) = f(z2), ... .
Taj niz zovemo orbita nelinearnog procesa
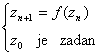 .
Skup
.
Skup 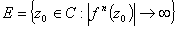 zovemo "odbojni skup"
(engl. espace set) danog
procesa. To je skup svih onih početnih
z0 kojima su orbite neograničene.
Granica ovog skupa zove se "Juliaov skup"
danog procesa. Naziv je dobila u čast francuskog matematičara
Gastona Julia (čitaj Žuliá).
zovemo "odbojni skup"
(engl. espace set) danog
procesa. To je skup svih onih početnih
z0 kojima su orbite neograničene.
Granica ovog skupa zove se "Juliaov skup"
danog procesa. Naziv je dobila u čast francuskog matematičara
Gastona Julia (čitaj Žuliá).
Za kvadratni proces 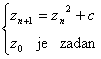 pripadni Juliaov skup za svaki konkretni dani kompleksni broj c obilježavamo s Jc, dok
odbojni skup obilježavamo s Ec.
pripadni Juliaov skup za svaki konkretni dani kompleksni broj c obilježavamo s Jc, dok
odbojni skup obilježavamo s Ec.
Naprimjer, izračunajmo neke točke iz
odbojnog skupa Ec
i njegovog komplementa za c = -0.5
+ 0.5i
|
|
Orbita1 | Orbita
2 |
Orbita
3 |
| x |
y |
x |
y |
x |
y |
|
| z0 |
0.000 |
0.000 |
0.500 |
-0.250 |
-0.250 |
-0.500 |
| z1 | -0.500 | 0.500 | -0.313 |
0.250 |
-0.688 |
0.250 |
| z2 | -0.500 | 0.000 |
-0.465 |
0.344 |
-0.090 |
0.156 |
| z3 | -0.250 |
-0.500 | -0.402 |
0.180 |
-0.516 |
0.472 |
| z4 | -0.688 |
0.250 | -0.371 |
0.355 |
-0.456 |
0.013 |
| z5 | -0.090 | 0.156 | -0.488 | 0.237 | -0.292 | 0.488 |
| z100 | -0.473 |
0.291 |
-0.393 |
0.290 |
-0.438 |
0.217 |
| z200 | -0.349 |
0.279 |
-0.411 |
0.271 |
-0.409 |
0.290 |
| z300 | -0.411 | 0.273 |
-0.409 |
0.276 |
-0.407 |
0.272 |
| z400 | -0.408 | 0.276 | -0.409 | 0.275 | -0.409 | 0.276 |
| z500 | -0.409 | 0.275 | -0.409 | 0.275 | -0.409 | 0.275 |
Slika 1. Točke iz komplementa odbojnog
skupa za c = -0.5 + 0.5i

|

|

|

|
| Slika
2. Juliaov skup za c=-0.5+0.5i |
Slika
3. Juliaov skup za c=-1 |
Slika
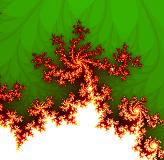
4. Juliaov skup za c=-0.049733-0.667582i |
Slika
5. Juliaov skup za c=-0.555468+0.494062i |
Mandelbrotov skup
|
|
Mandelbrotov skup M, po definiciji,
sadrži sve kompleksne
brojeve c za koje je pripadni Juliaov
skup Jc kvadratnog procesa 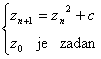 povezan, odnosno:
povezan, odnosno: 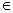 C : Jc je povezan }.
C : Jc je povezan }.
|
| Slika
6. Mandelbrotov skup |
Može se dokazati da je skup Jc povezan
ako i samo ako je orbita početne točke
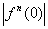 ne teži u beskonačnost, tj.
ne teži u beskonačnost, tj. 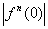 je omeđen niz. je omeđen niz. |

|

|
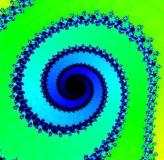
| Slika 7. Povezani Juliaov skup | Slika 8. Nepovezani Juliaov skup |
|

|

|
|
| Slika 9. | Slika 10.
|
Slika 11. | Slika 12. |
Cantorova prašina i gredice

Slika 13. Cantorova prašina – konstrukcija
Neka je F Cantorov skup konstruiran kao presjek
zatvorenih skupova E0, E1, E2 , ... .
Skup E0 je interval [0, 1]. E1 se
dobiva iz E0
uklanjanjem srednje trećine (otvoreni skup (1/3, 2/3)), E2 se
dobiva iz E1 uklanjanjem srednjih trećina (otvorenih
skupova (1/9, 2/9) i (7/9, 8/9)) ... .
F sadrži beskonačan niz "unutrašnjih rubnih točkaka" od intervala
dobivenih u svakom koraku, odnosno 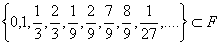 .
.
Cantorov skup je neprebrojiv, odnosno ne postoji način numeracije svih
točaka od F. Preciznije vrijedi:
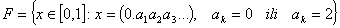
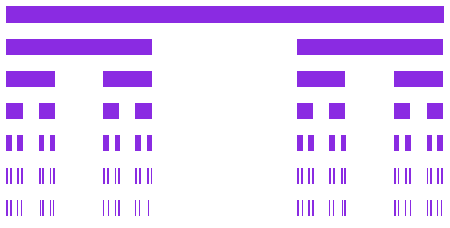
Slika 14. Cantorova prašina
(gredice)
Igra kaosa
Primjer:
Neka je zadan trokut ABC. Slučajno biramo početnu točku x0 iz unutrašnjosti trokuta. Nasumično odaberemo jedan od vrhova trokuta ABC s oznakom random(ABC) te izaberemo još jednu točku unutar trokuta koja je na pola puta između x0 i random(ABC)... i tako dalje : xn+1 = (xn + random(ABC))/2.
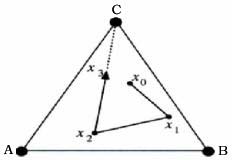
Slika 15. Igra kaosa – početak
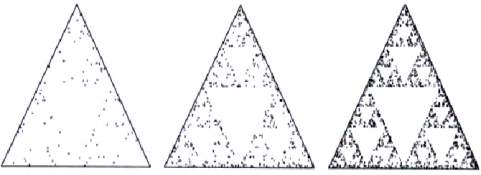
| 500 točaka | 1000 točaka | 1500 točaka |
Slika 16. Igra kaosa - međurezultati
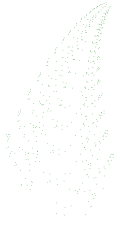
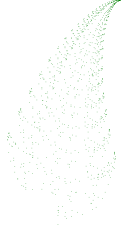
Na sličan način možemo dobiti i razne druge oblike kao npr. grančicu.
|
|

|

|
| 500 točaka | 1000 točaka | 4000 točaka | krajnji rezultat |
Slika17. Igra kaosa – nastanak grančice
Pitagorino stablo
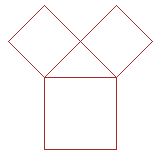 |
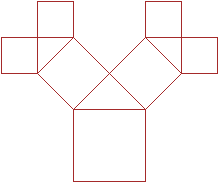 |
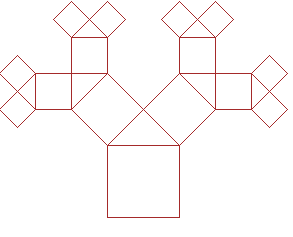 |
| 1 iteracija |
2 iteracija |
3 iteracija |
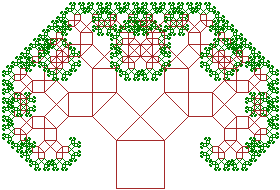 |
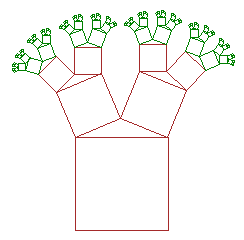 |
| Slika 19. Pitagorino stablo -
konačan
rezultat |
Slika 20. Pitagorino drvo (gornji kut 120o,
lijevi kut 30o ) |
|
|
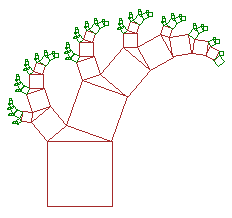 |
| Slika 21. Pitagorino stablo (brokula) (gornji kut 90o, lijevi kut 30o ) |
Slika 22. Pitagorino stablo (brokula) (gornji kut 120o, lijevi kut 40o ) |
Kochova krivulja i pahuljica
|
|
|
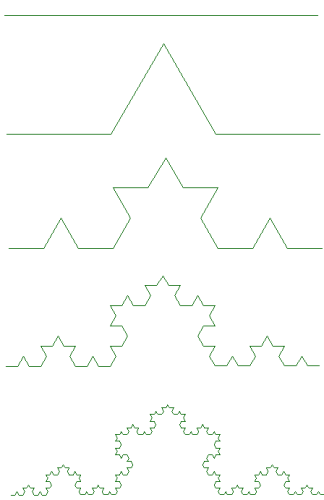
| Slika 23. Kochova krivulja – nastanak | Slika 24. Kochova pahuljica – nastanak |
Kochovu krivulju uveo je švedski matematičar Helge von Koch.
Fraktalna dimenzija Kochove krivulje je log 4 / log 3 = 1.2618... .
|
|
|
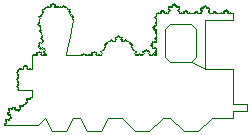
| Slika 25. Zvjezdica | Slika
26. Vlak u snijegu |
Sierpinskijev trokut
Sierpinskijev trokut uveo je poljski matematičar Waclaw
Sierpinski.
Fraktalna dimenzija Sierpinskijevog trokuta iznosi

Slika 27. Sierpinskijev trokut – konstrukcija otkidanjem trokuta
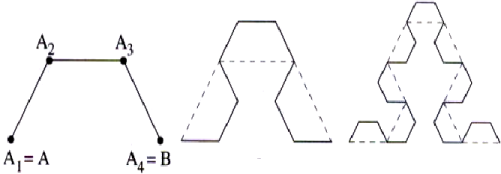
Slika 28. Sierpinskijev trokut – konstrukcija krivuljama
|
|
| Slika 29. Sierpinskijev trokut – konstrukcija krivuljama |
Program i rad s programom
Program Galerija ULTIMATE (300KB) je pisan u programskom jeziku C# za čiji je rad potreban .NET framework koji se može naći na CD-ovima nekih informatičkih časopisa (npr. mrež@, BUG, VIDI, ... ) ili s adrese http://msdn.microsoft.com/netframework/technologyinfo/howtoget/default.aspx, treba "skinuti" "Microsoft .NET Framework 1.1 Redistributable".
Ako koristite MS Internet Explorer , za "skidanje" galerije kliknite desnu tipku miša te odaberite "Save target as...".
Rad s Mandelbrotovim i Juliaovim skupovima
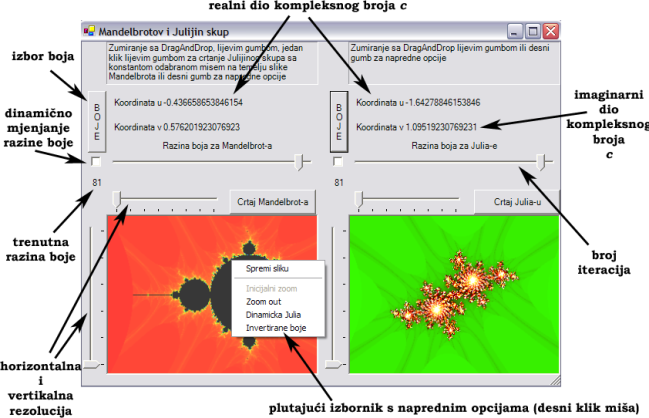
Rad sa ostalim fraktalima

Implementacija programa
Kao što je gore navedeno, program je pisan u programskom jeziku C# u MS Visual Studio .NET okruženju. Program se sastoji od niza razreda od kojih svaki sadrži implementaciju jednog ili jedne skupine algoritama za prikaz fraktala u ravnini. Klikom na sličicu fraktala na osnovnoj formi (strogo uređen prozor) stvara se (instancira) novi primjerak objekta dotičnog razreda zaduženog za prikaz željenog fraktala. Ovo svojstvo omogućava "otvaranje" više primjeraka istog prozora. Svi prozori omogućavaju skoro po volji skaliranje. Velik prozor će možda povećati užitak gledanja fraktala, ali će ujedno usporiti njihovo iscrtavanje.
Mandelbrotov i Juliaov skup
Mandelbrotov i Juliaov skup se
iscrtavaju tako
da se svaka točka zaslona (dijela zaslona namijenjenog za prikaz slike
fraktala) preslika u kompleksnu ravninu u kojoj je definiran gore
naveden kvadratni proces, te numerički
ispituje "brzina konvergencije" niza kompleksnih brojeva z0, z1,
z2,
... . Ovisno o brzini konvergencije određuje se boja točke na zaslonu.
Za detaljnije upute o implementaciji pogledajte : http://www.zemris.fer.hr/predmeti/rg/labosi/vj9.htm.
Igra kaosa
U razredu koji implementira prikaze fraktala zasnovanih na igri kaosa postoje mnogi, u osnovi vrlo slični, algoritmi. Neki su vrlo jednostavni i u ideji se ne razlikuju mnogo od gore navedenog algoritma za iscrtavanje Sierpinskijevog trokuta. Dodatno objašnjenje dotičnog algoritma se može naći na : http://www.jcu.edu/math/vignettes/ChaosGame.htm.Velika većina ostalih algoritama se bazira na IFS (engl. iterated function sheme) jednadžbama:
yn+1 = c xn + d yn + f.
Pitagorino stablo i Cantorova prašina
Implementacija prikaza Pitagorinog stabla i Cantorove prašine (gredica) vrlo je jednostavna i svodi se na kratke rekurzivne algoritme. Jedina opaska je da korisnik može pretjerati s dubinom (tj. brojem iteracija) i time vrlo znatno usporiti iscrtavanje dotičnog fraktala. Kako veličine iscrtavanih linija konvergiraju prema nuli, tako će se kod većeg broja iteracija dogoditi da računalo izračunava pozicije i veličine linija koje se u opće ne mogu prikazati, tj. zbog konačne razlučivosti zaslona i ljudske nemogućnosti raspoznavanja vrlo sitnih objekata, sve sljedeće iscrtane linije nakon neke iteracije neće pridonijeti nikakvom poboljšanju slike. Problem se vrlo lagano riješava. Nakon određene prekidne (engl. cut-off) veličine, sve daljnje iteracije u dotičnom smjeru su obustavljene. Autori su se ugodno iznenadili velikom ubrzanju iscrtavanja nakon primjene navedenog pravila.Krivulje
Prikaz fraktala zasnovanih na krivuljama je u osnovi najjednostavnijii najlakše se improvizacijom stvaraju novi fraktali. Svi algoritmi su rekurzivne prirode kao i kod Pitagorinog stabla i Cantorove prašine, te vrijede iste opaske. Algoritmi se svode na višestruko prelamanje početne krivulje (dužine) pod nekim kutovima, te onda nastavak prelamanja na već prelomljene dijelove.Za daljna objašnjenja možete pogledati http://www.jcu.edu/math/vignettes/koch.htm.
Sierpinskijev trokut i ostali fraktali
Prikazi zadnje veće skupine fraktala zasnivaju se na jednostavnim linearnim transformacijama kao što su: pomak, skaliranje, rotacija i smik. Rekurzivnom primjenom istog pravila iz koraka u korak mogu se dobiti vrlo zanimljivi fraktali.Osim već navedene skupine u ovom razredu su implementirana još dva algoritma. Jedan je vrlo specifičan algoritam koji se temelji na Pascalovom trokutu, dok je drugi (Brod) ekvivalentan algoritmu iscrtavanja Mandelbrotovog i Juliaovog skupa, samo za drugačiji nelinearni proces z = ( |x| + i*|y| )2 + c.