		Hrvatski matematički elektronski časopis math.e
		Broj 6
		http://web.math.hr/mathe/

Rješenja nagradnih zadataka

Ovi zadaci postavljeni su u 6. broju math.e. Nažalost do izlaska 8. broja nismo dobili nijedno točno rješenje. Ovdje objavljujemo rješenja postavljenih zadataka.

Rješenje prvog zadatka

U prvom zadatku trebalo je dokazati da u ravnini kojoj je svaka točka obojana jednom od konačno mnogo boja postoji pravokutnik s jednako obojanim vrhovima. Ovaj zadatak rješava se primjenom Dirichletovog principa.

Neka su točke ravnine obojane s ukupno n boja. Promotrimo točke s koordinatama (i, j), za i = 1, 2,...,M, j = 1, 2,...,N. Za čvrst j točke (1, j), (2, j), ..., (M, j) možemo obojati na n^M načina. Prema tome, ako je N > n^M, postoje indeksi j₁ i j₂ takvi da su točke (i, j₁) i (i, j₂) obojane istom bojom, za i = 1, 2,...,M. Ako je pak M > n + 1 postoje indeksi i₁, i₂ takvi da su točke (i₁, j₁) i (i₂, j₁) obojane istom bojom. Tom su bojom obojane i točke (i₁, j₂) i (i₂, j₂) pa za dovoljno velike M i N dobivamo pravokutnik s jednako obojanim vrhovima.

Rješenje drugog zadatka

U drugom zadatku trebalo je dokazati da se svaki dijadski razlomak (broj oblika m/2ⁿ) može reprezentirati pomoću igre Hackenbush s jednim stupcem. Trebalo je naći reprezentacije brojeva 151/64 i 1/3.

Reprezentacija dijadskih razlomaka izgleda ovako:

Predznak određuje boja segmenta koji dira tlo (plus ako je plavi, a minus ako je crveni).
Prvi par različito obojanih segmenata predstavlja decimalnu točku.
Broj segmenata ispod "decimalne točke" predstavlja cjeli dio broja.
Segmenti iznad "decimalne točke" određuju binarne decimalne znamenke: 1 ako se boja podudara s bojom prvog segmenta, a 0 ako se ne podudara. Na kraju je potrebno još dopisati jednu dodatnu decimalnu znamenku 1.

Na primjer, razlomak 151/64 reprezentiran je lijevim Hackenbush stupcem na slici:

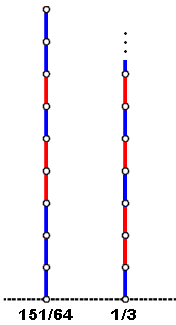
Za sve brojeve kojima decimalni zapis u bazi 2 nije konačan potreban je Hackenbush stupac beskonačne duljine. Na primjer, 1/3=(0.01010101...)₂ pa njegova Hackebush reprezentacija izgleda kao desni stupac na slici. Na tlu je plavi segment, iznad njega dva crvena, a nakon toga alterniraju plavi i crveni segmenti.