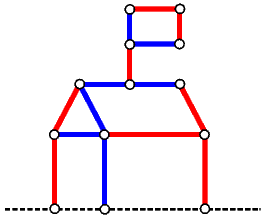
1. Svaka točka ravnine je obojena u jednu od konačno mnogo danih boja. Dokažite da u ravnini postoji pravokutnik čiji svi vrhovi imaju istu boju.

2. Hackenbush je igra za dva igrača koja je zadana određenim brojem obojenih linijskih segmenata, od kojih su neki međusobno povezani, dok su neki povezani s “tlom”. Plavi segmenti pripadaju lijevom igraču, a crveni segmenti desnom. Primjer jedne Hackenbush igre prikazan je na slijedećoj slici:

Igrač koji je u danom trenutku na potezu mora obrisati proizvoljni segment među onima koji mu pripadaju. Pri tome, svi segmenti koji nakon toga prestaju biti povezani s “tlom” također bivaju obrisani. Primjerice, ukoliko desni igrač obriše stijeg koji nosi zastavu na krovu kuće, nestat će također i zastava:

Igrači naizmjenično biraju segmente, te kao i u dosadašnjim igrama, u igri pobjeđuje onaj igrač koji odigra posljednji potez. Dakle, onaj igrač kojemu više ne preostane niti jedan segment za obrisati, gubi igru.

Svaki primjerak Hackenbusha odgovara jednoj od apstraktnih igara iz teksta o kombinatornim igrama. Primjerice, slijedeća slika prikazuje Hackenbush igre stupnja 0, 1 i 2:

Uočite kako je Hackenbush primjer igre koja nije imparcijalna, budući u njoj igrači u nemaju na raspolaganju jednake skupove opcija za odigrati (dakle, na nju nije moguće primijeniti Sprague-Grundyjevu teoriju). Ipak, ova igra ima neka druga zanimljiva svojstva. Pogledajmo još nekoliko jednostavnih primjeraka Hackenbush igara, te kojim apstraktnim igrama one odgovaraju:

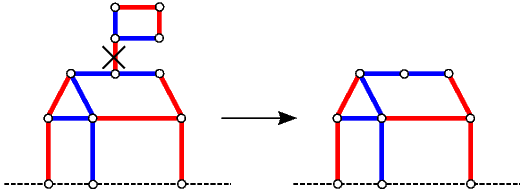
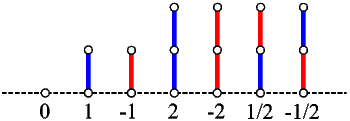
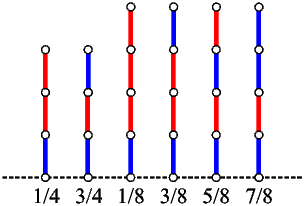
Dokažite da se svaki dijadski razlomak, tj. racionalni broj oblika , gdje je m , a n , može reprezentirati pomoću jednostupčanog Hackenbusha. Koja je reprezentacija broja 151/64?
Kako pomoću jednostupčanog Hackenbusha reprezentirati razlomak koji nije dijadski, npr. ?

Rješenja zadataka