
Broj 6






















Vjekoslav Kovač
Kromatski broj ravnine - neriješeni problem o bojenju


Sadržaj:
1. Uvod
2. Formulacija problema i osnovni rezultati
3. Pokušaji popravljanja donje ograde
4. Pokušaji popravljanja gornje ograde
5. Veza s teorijom grafova i logikom sudova
6. Bojenje racionalnih točaka
7. Pravac, ravnina, 3D-prostor ...
8. Je li lakše obojiti sferu?
9. Bojenje metričkog prostora
10. Umjesto zaključka
Literatura
1. Uvod
U ovom članku upoznat ćemo se s jednim problemom iz kombinatorne geometrije, koji je zbog svoje elegancije i prividne jednostavnosti tijekom više od pola stoljeća zaokupljao umove mnogih slavnih matematičara. Premda do danas nije riješen, doprinio je razvoju mnogih matematičkih disciplina, od kombinatorike (npr. teorija grafova, Ramseyeva teorija) do geometrije (npr. popločavanja, pakiranja), a neki mu aspekti zadiru i u pitanja matematičke logike.
Čini se da je problem prvi postavio 18-godišnji Edward Nelson 1950. godine premda su do njega nezavisno došli P. Erdös i H. Hadwiger. Među ostalim poznatim matematičarima koji su se bavili ovim problemom nalaze se i R. Graham i E. Szemeredi. Spominje ga i M. Gardner 1960. godine u svojoj kolumni Matematičke igre popularno-znanstvenog časopisa Scientific American [Gar].
U posljednjih 50-ak godina o problemu je napisano nekoliko desetaka znanstvenih radova i mi ćemo ovdje ukratko izložiti najzanimljivije od dobivenih djelomičnih rezultata. Imat ćemo priliku na lijepom primjeru demonstrirati tipični put matematičkog istraživanja: kako jedan zanimljiv problem evoluira u mnoge druge, kako se raznovrsne matematičke teorije međusobno obogaćuju i kako je u matematičkom istraživanju moguće ostvariti važan napredak, a da se uopće ne odgovori na prvotno postavljeno pitanje.
2. Formulacija problema i osnovni rezultati
Evo osnovnog problema:
| Koliko je najmanje boja potrebno da bismo obojili sve točke ravnine tako da nikoje dvije jednako obojene točke ne budu međusobno udaljene točno za 1? |
Najmanji potrebni broj boja zvat ćemo kromatski broj ravnine i označivati
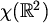 .
(Naziv i oznaku obrazložit ćemo u točki 5.)
Za svako bojenje ravnine sa svojstvom da ne postoje istobojne točke udaljene za 1
reći ćemo da je pravilno bojenje.
.
(Naziv i oznaku obrazložit ćemo u točki 5.)
Za svako bojenje ravnine sa svojstvom da ne postoje istobojne točke udaljene za 1
reći ćemo da je pravilno bojenje.
Možemo li relativno jednostavno zaključiti nešto o broju
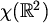 ?
Kao prvo, primijetimo da vrhovi svakog jednakostraničnog trokuta moraju biti različito obojeni
pa je nužno koristiti barem 3 boje. Ipak, one još nisu dovoljne, što se vidi iz
konfiguracije točaka nazvane Moserovo vreteno (prema matematičaru
L. Moseru, koji se prvi dosjetio ovog primjera).
Sve dužine označene na slici imaju duljinu 1.
?
Kao prvo, primijetimo da vrhovi svakog jednakostraničnog trokuta moraju biti različito obojeni
pa je nužno koristiti barem 3 boje. Ipak, one još nisu dovoljne, što se vidi iz
konfiguracije točaka nazvane Moserovo vreteno (prema matematičaru
L. Moseru, koji se prvi dosjetio ovog primjera).
Sve dužine označene na slici imaju duljinu 1.
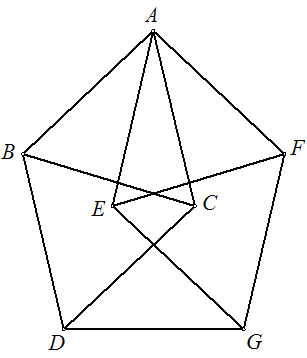
Doista, pretpostavimo da je 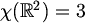 ,
tj. da postoji pravilno bojenje u 3 boje.
Iz jednakostraničnih trokuta na slici zaključujemo da su točke A i D istobojne,
a jednako tako točke A i G, no to nije moguće jer su D i G udaljene za 1.
Dakle,
,
tj. da postoji pravilno bojenje u 3 boje.
Iz jednakostraničnih trokuta na slici zaključujemo da su točke A i D istobojne,
a jednako tako točke A i G, no to nije moguće jer su D i G udaljene za 1.
Dakle, 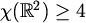 .
.
S druge strane, nije odmah jasno da je pravilno bojenje (u konačno mnogo boja) uopće moguće. Ipak, nakon malo isprobavanja lako dolazimo do sljedećeg pravilnog bojenja u 7 boja:

Boje se ponavljaju periodički. Drugi način gledanja na gornju sliku jest da uočimo ponavljanje "cvjetnog uzorka":

Pravilni šesterokuti na slici imaju stranicu duljine 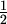 .
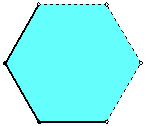
Osim toga, svakom šesterokutu uključujemo tri stranice i dva vrha,
kako je prikazano na slici, a isključujemo ostale točke ruba.
(To je nužno da bi šesterokuti doista činili particiju ravnine.)
.
Osim toga, svakom šesterokutu uključujemo tri stranice i dva vrha,
kako je prikazano na slici, a isključujemo ostale točke ruba.
(To je nužno da bi šesterokuti doista činili particiju ravnine.)
Uzmimo sada npr. dvije crvene točke. Ako pripadaju istom šesterokutu, onda su udaljene
za manje od 1 (koliko je duga najdulja dijagonala šesterokuta),
a ako pripadaju različitim šesterokutima, udaljenost im je veća od
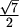 .
Dakle, doista nikoje dvije istobojne točke nisu udaljene za 1.
Time smo pokazali da je 7 boja dovoljno premda bismo možda mogli proći i ekonomičnije.
U svakom slučaju, dokazali smo osnovni rezultat:
.
Dakle, doista nikoje dvije istobojne točke nisu udaljene za 1.
Time smo pokazali da je 7 boja dovoljno premda bismo možda mogli proći i ekonomičnije.
U svakom slučaju, dokazali smo osnovni rezultat:
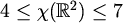 ,
tj. ,
tj. 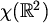 je 4, 5, 6, ili 7. je 4, 5, 6, ili 7.
|
Zvuči nevjerojatno, ali do danas nije poznato ništa više o samom broju 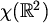 ,
tj. još uvijek imamo četiri mogućnosti.
Neki su matematičari čak javno iznosili svoje slutnje o broju
,
tj. još uvijek imamo četiri mogućnosti.
Neki su matematičari čak javno iznosili svoje slutnje o broju 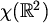 ,
naravno, bazirane na heurističkom rasuđivanju bez strogog dokaza.
Ostavit ćemo čitatelju da na temelju djelomičnih rezultata iz narednih točaka odabere svog "favorita"
za vrijednost
,
naravno, bazirane na heurističkom rasuđivanju bez strogog dokaza.
Ostavit ćemo čitatelju da na temelju djelomičnih rezultata iz narednih točaka odabere svog "favorita"
za vrijednost 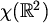 .
.
Drugi primjer pravilnog bojenja u 7 boja jest ovo šareno popločavanje ravnine kvadratima:

Kvadrati imaju stranicu duljine 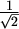 ,
a svaki red kvadrata dobiva se iz gornjeg reda
translacijom ulijevo za vektor duljine
,
a svaki red kvadrata dobiva se iz gornjeg reda
translacijom ulijevo za vektor duljine 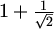 .
Svakom kvadratu uključujemo lijevu i donju stranicu te donji lijevi vrh,
a oduzimamo mu ostale točke ruba.
.
Svakom kvadratu uključujemo lijevu i donju stranicu te donji lijevi vrh,
a oduzimamo mu ostale točke ruba.

Za još jedan primjer bojenja pogledajte [Pegg].
3. Pokušaji popravljanja donje ograde
S obzirom da nije poznato pravilno bojenje ravnine u manje od 7 boja, mnogi su matematičari pokušali popraviti donju procjenu 4 za broj potrebnih boja. Prirodno je proučavati takva bojenja gdje skupovi koje čine sve točke iste boje imaju još neko lijepo svojstvo. Ako od bojenja još zahtijevamo da bude izmjerivo (tj. da čini particiju ravnine na Lebesgue-izmjerive skupove), onda je nužno koristiti barem 5 boja [Fal]. Drugim riječima, izmjerivi kromatski broj ravnine je barem 5.
Svaki podskup ravnine koji "konstruktivno zadamo" (ovdje to znači: bez korištenja aksioma izbora) bit će Lebesgue-izmjeriv. To znači da ako pravilno bojenje u 4 boje uopće postoji, sigurno ga nećemo moći nacrtati, tj. izgledat će (barem u nekom svom dijelu) otprilike ovako:

Naravno, zbog konačne rezolucije ekrana ni ova slika nije dobra. Želimo samo sugerirati kako "nekonstruktivna slika" nužno mora izgledati nesvakidašnje komplicirano.
Već ovaj rezultat pokazuje koliko je problem logički suptilan.
Naime, izostavljanjem aksioma izbora moguće je konstruirati model teorije skupova
u kojem je svaki podskup ravnine Lebesgue-izmjeriv ([Sol]) pa u takvom "svijetu"
vrijedi 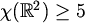 .
Ipak, većina matematičara živi i radi u
Zermelo-Fraenkelovoj teoriji skupova
s aksiomom izbora pa je za nas ipak moguće
.
Ipak, većina matematičara živi i radi u
Zermelo-Fraenkelovoj teoriji skupova
s aksiomom izbora pa je za nas ipak moguće 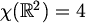 .
O takvim logičkim začkoljicama bit će još riječi u točki 5.
.
O takvim logičkim začkoljicama bit će još riječi u točki 5.
Ako od skupova određenih bojama tražimo da budu "još ljepši" (unije područja omeđenih
po dijelovima glatkim krivuljama, pri čemu točke na rubovima pripadaju nekom od susjednih područja),
onda je za dobro bojenje nužno koristiti barem 6 boja [Wood].
Naprimjer, takvi su svi gornji primjeri bojenja: tamo su jednobojni skupovi čak unije mnogokuta.
Teško je i zamisliti bojenje koje nema ovo svojstvo pa će čitatelji s klasičnim geometrijskim zorom
(i koji vjeruju da u matematici lijepi problemi moraju imati lijepa rješenja)
sigurno poželjeti da je 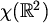 jednak 6 ili 7.
jednak 6 ili 7.
4. Pokušaji popravljanja gornje ograde
U prethodnoj točki vidjeli smo ozbiljna ograničenja koja susrećemo kad želimo
pravilno obojiti ravninu u 4 ili 5 boja.
Ipak, nađena su neka "gotovo pravilna" bojenja ravnine u 6 boja, koja sugeriraju
da možda vrijedi 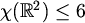 .
Naredni primjeri precrtani su iz [Soi1], [HS].
.
Naredni primjeri precrtani su iz [Soi1], [HS].
Za bojenje ravnine u k boja (nazovimo ih 1,2,...,k) kažemo da je tipa
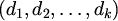 ako nikoje dvije točke boje i nisu udaljene za
ako nikoje dvije točke boje i nisu udaljene za
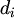 , i=1,...,m.
Egzistencija 6-bojenja tipa (1,1,1,1,1,1) značila bi
, i=1,...,m.
Egzistencija 6-bojenja tipa (1,1,1,1,1,1) značila bi 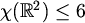 .
Prilično smo blizu toga: nađeno je 6-bojenje tipa
(1,1,1,1,1,
.
Prilično smo blizu toga: nađeno je 6-bojenje tipa
(1,1,1,1,1,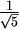 ).
).

Siva boja na slici ne realizira udaljenost 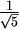 ,
a ostale boje ne realiziraju udaljenost 1.
Osmerokuti imaju stranice duljina
,
a ostale boje ne realiziraju udaljenost 1.
Osmerokuti imaju stranice duljina
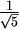 i
i 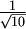 ,
kvadratići imaju duljinu stranice
,
kvadratići imaju duljinu stranice 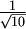 .
.

Zanimljivo je i ovo 6-bojenje tipa (1,1,1,1,1,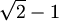 ).
).

Duljina stranice svakog kvadrata je 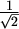 ili
ili 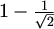 .
.
5. Veza s teorijom grafova i logikom sudova
Sada je vrijeme da koncept bojenja podignemo na formalno višu razinu.
(Jednostavni neusmjereni) graf uređeni je par G=(V,E) skupa V i
irefleksivne simetrične binarne relacije E na skupu V.
Elemente skupa V zovemo vrhovi grafa, a elemente relacije E zovemo
bridovi grafa te kažemo da su dva vrha susjedna (ili da su spojena bridom) ako
je taj par vrhova u relaciji E.
(Primijetimo da prema našoj definiciji V i E mogu biti beskonačni premda se u
teoriji grafova
najčešće proučavaju konačni grafovi.)
Naprimjer, označimo s 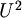 graf kojem je skup vrhova
graf kojem je skup vrhova 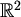 ,
a dvije točke su susjedne ako i samo ako su udaljene za 1.
,
a dvije točke su susjedne ako i samo ako su udaljene za 1.
Kažemo da je graf k-obojiv (k je prirodan broj) ako mu je skup vrhova moguće
particionirati u k podskupova (to su "boje") tako da nikoja dva vrha iz istog podskupa nisu susjedna.
Kromatski broj grafa
G je najmanji k takav da je graf k-obojiv,
a označavamo ga 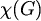 .
(Moguće je i da takav prirodni broj uopće ne postoji.)
Primijetimo da naš osnovni problem zapravo traži da izračunamo
.
(Moguće je i da takav prirodni broj uopće ne postoji.)
Primijetimo da naš osnovni problem zapravo traži da izračunamo
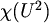 .
Graf
.
Graf 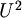 može se prirodno nazvati
ravnina jediničnih udaljenosti pa stoga
može se prirodno nazvati
ravnina jediničnih udaljenosti pa stoga
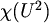 zovemo kromatski broj ravnine.
Radi jednostavnosti umjesto
zovemo kromatski broj ravnine.
Radi jednostavnosti umjesto 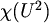 pišemo
pišemo
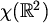 .
.
Podgraf
grafa G=(V,E) je svaki graf G'=(V',E')
takav da su V' i E' redom podskupovi od V i E.
Npr. Moserovo vreteno jedan je konačni podgraf grafa 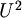 .
Fundamentalni rezultat o bojenju beskonačnih grafova je
de Bruijn-Erdösev teorem [BE]:
.
Fundamentalni rezultat o bojenju beskonačnih grafova je
de Bruijn-Erdösev teorem [BE]:
| Graf je k-obojiv ako i samo ako je svaki njegov konačni podgraf k-obojiv. |
U vezi s našim problemom to znači da je dovoljno bojiti konačne konfiguracije točaka ravnine.
Tako bi, naprimjer, za dokaz hipoteze 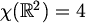 bilo dovoljno dokazati da je svaki konačni skup točaka ravnine
obojiv u 4 boje tako da nema istobojnih točaka udaljenih za 1.
Ovaj pristup omogućava primjenu brojnih tehnika teorije (konačnih) grafova
i dobiveni su neki parcijalni rezultati, ali sama hipoteza nije ni dokazana ni opovrgnuta.
Eventualni nedostatak pristupa je to što se ovaj teorem dokazuje korištenjem nekog od ekvivalenata
aksioma izbora
i dokaz mu nije nimalo konstruktivan.
Zato čak i da uspijemo dokazati kako je svaki konačni podgraf od
bilo dovoljno dokazati da je svaki konačni skup točaka ravnine
obojiv u 4 boje tako da nema istobojnih točaka udaljenih za 1.
Ovaj pristup omogućava primjenu brojnih tehnika teorije (konačnih) grafova
i dobiveni su neki parcijalni rezultati, ali sama hipoteza nije ni dokazana ni opovrgnuta.
Eventualni nedostatak pristupa je to što se ovaj teorem dokazuje korištenjem nekog od ekvivalenata
aksioma izbora
i dokaz mu nije nimalo konstruktivan.
Zato čak i da uspijemo dokazati kako je svaki konačni podgraf od 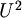 4-obojiv,
još uvijek ne bismo znali "kako izgleda" neko dobro 4-bojenje cijele ravnine.
(Sjetimo se razmatranja iz točke 3.)
4-obojiv,
još uvijek ne bismo znali "kako izgleda" neko dobro 4-bojenje cijele ravnine.
(Sjetimo se razmatranja iz točke 3.)
Skicirajmo dokaz de Bruijn-Erdösevog teorema. On je direktna posljedica teorema kompaktnosti u logici sudova:
| Skup formula je ispunjiv ako i samo ako je svaki njegov konačni podskup ispunjiv. |
Za definicije spomenutih pojmova čitatelja upućujemo na skriptu [Vuk]. Napomenimo samo da skup propozicionalnih varijabli iz alfabeta logike sudova ne mora biti prebrojiv, a teorem kompaktnosti vrijedi i u toj općenitosti. Potrebno je samo malo modificirati dokaz iz [Vuk] te iskoristiti neki ekvivalent aksioma izbora, npr. Zornovu lemu.
Dakle, neka je G=(V,E) graf i pretpostavimo da je svaki njegov konačni podgraf
k-obojiv; boje ćemo zvati 1,2,...,k.
Promatramo logiku sudova kojoj je skup propozicionalnih varijabli jednak
V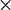 {1,2,...,k}.
Označimo s
{1,2,...,k}.
Označimo s 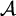 skup koji sadrži sljedeće formule:
skup koji sadrži sljedeće formule:
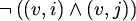 , za svaki
, za svaki
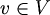 te svake
te svake 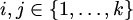 ,
,
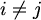 ,
,
čitamo: "vrh v nije istovremeno obojen različitim bojama i i j"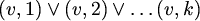 , za svaki
, za svaki
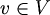 ,
,
čitamo: "vrh v je obojen barem jednom bojom"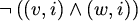 , za svake
, za svake
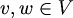 ,
, 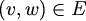 te svaki
te svaki 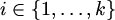 ,
,
čitamo: "susjedni vrhovi v i w nisu obojeni istom bojom i".
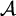 ispunjiv,
tj. da postoji interpretacija I koja sve formule iz
ispunjiv,
tj. da postoji interpretacija I koja sve formule iz 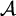 valuira kao "istina".
Tada ćemo vrh v obojiti bojom i ako i samo ako je I(v,i)="istina".
Zbog teorema kompaktnosti dovoljno je pokazati da je svaki konačni podskup od
valuira kao "istina".
Tada ćemo vrh v obojiti bojom i ako i samo ako je I(v,i)="istina".
Zbog teorema kompaktnosti dovoljno je pokazati da je svaki konačni podskup od
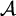 ispunjiv.
Svaki konačni skup formula koristi samo konačno mnogo propozicionalnih varijabli
pa se u njemu pojavljuje konačno mnogo elemenata od V.
Podgraf od G generiran tim konačnim skupom vrhova po pretpostavci je k-obojiv.
Jedno njegovo dobro k-bojenje definira vrijednosti neke parcijalne interpretacije
koja valuira "istina" sve formule iz razmatranog konačnog podskupa od
ispunjiv.
Svaki konačni skup formula koristi samo konačno mnogo propozicionalnih varijabli
pa se u njemu pojavljuje konačno mnogo elemenata od V.
Podgraf od G generiran tim konačnim skupom vrhova po pretpostavci je k-obojiv.
Jedno njegovo dobro k-bojenje definira vrijednosti neke parcijalne interpretacije
koja valuira "istina" sve formule iz razmatranog konačnog podskupa od
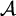 , tj. on je ispunjiv.
, tj. on je ispunjiv.
Toliko o matematičkoj logici. Vraćamo se elementarnijim stvarima!
6. Bojenje racionalnih točaka
Racionalna točka u 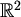 točka je kojoj su obje koordinate racionalni brojevi, tj. element od
točka je kojoj su obje koordinate racionalni brojevi, tj. element od
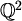 .
Takvih točaka ima samo prebrojivo mnogo, dakle "mnogo manje" nego svih točaka ravnine
pa se možemo nadati da će kromatski broj podgrafa
.
Takvih točaka ima samo prebrojivo mnogo, dakle "mnogo manje" nego svih točaka ravnine
pa se možemo nadati da će kromatski broj podgrafa 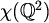 biti manji nego kromatski broj cijelog grafa.
(Prethodna točka naučila nas je da ipak moramo biti suzdržani s takvim konstatacijama.)
Srećom, ovdje je situacija doista takva [Wood]:
biti manji nego kromatski broj cijelog grafa.
(Prethodna točka naučila nas je da ipak moramo biti suzdržani s takvim konstatacijama.)
Srećom, ovdje je situacija doista takva [Wood]:
Graf 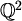 je bipartitan pa je je bipartitan pa je
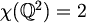 . .
|
Za graf kažemo da je bipartitan ako mu se skup vrhova može rastaviti na dva podskupa tako da svaki brid spaja vrhove iz različitih podskupova. Drugim riječima, graf je bipartitan ako i samo ako je 2-obojiv.
Skicirat ćemo dokaz ove tvrdnje. Ciklus je put u grafu kojem se podudaraju početak i kraj. Poznati Königov teorem iz teorije grafova glasi:
| Graf je bipartitan ako i samo ako nema ciklusa neparne duljine. |
Pretpostavimo da u grafu 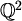 postoji ciklus duljine 2k+1.
To ima za posljedicu da u ravnini postoji 2k+1 vektora
postoji ciklus duljine 2k+1.
To ima za posljedicu da u ravnini postoji 2k+1 vektora
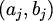 s racionalnim koordinatama, duljine 1 i kojima je zbroj nul-vektor.
s racionalnim koordinatama, duljine 1 i kojima je zbroj nul-vektor.
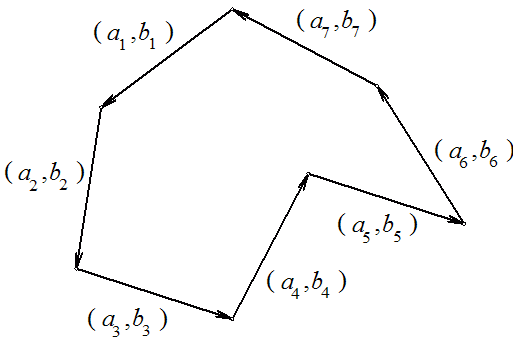
Iz teorema o
Pitagorinim trojkama
slijedi da su svi ti vektori oblika
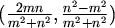 ili
ili
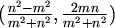 za neke cijele brojeve
m i n koji su relativno prosti i različite parnosti.
Primijetimo da razlomak
za neke cijele brojeve
m i n koji su relativno prosti i različite parnosti.
Primijetimo da razlomak 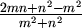 ima neparan brojnik
i nazivnik te da zbroj 2k+1
takvih razlomaka opet ima (i nakon eventualnog skraćivanja) neparan brojnik i nazivnik.
Zato taj zbroj ne može biti 0.
S druge je strane
ima neparan brojnik
i nazivnik te da zbroj 2k+1
takvih razlomaka opet ima (i nakon eventualnog skraćivanja) neparan brojnik i nazivnik.
Zato taj zbroj ne može biti 0.
S druge je strane 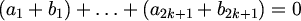 . Kontradikcija!
. Kontradikcija!
7. Pravac, ravnina, 3D-prostor ...
Prirodna generalizacija našeg problema jest određivanje kromatskog broja n-dimenzionalnog
euklidskog prostora 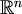 .
.
Za pravac (n=1) očigledno vrijedi 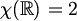 .
Točke iz
.
Točke iz 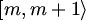 jednostavno bojimo
crveno za parne m, a zeleno za neparne.
jednostavno bojimo
crveno za parne m, a zeleno za neparne.
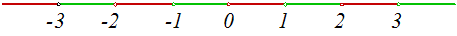
Vidjeli smo da u ravnini već postoje problemi, a u višim dimenzijama oni su još izraženiji.
Tek nedavno dobivene su ocjene 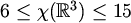 ([Cou],[Nech]), a u dimenzijama
([Cou],[Nech]), a u dimenzijama 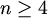 razmaci između donje i gornje ograde još su mnogo veći.
Što se tiče procjene broja
razmaci između donje i gornje ograde još su mnogo veći.
Što se tiče procjene broja 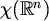 za velike n, dokazano je
za velike n, dokazano je
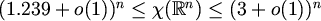 , kada
, kada 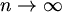 ,
,
što po definiciji znači
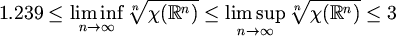 .
.
U svakom slučaju, niz 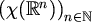 raste eksponencijalno.
raste eksponencijalno.
8. Je li lakše obojiti sferu?
Označimo sa 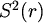 (dvodimenzionalnu) sferu
u
(dvodimenzionalnu) sferu
u 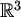 oko ishodišta polumjera r.
Želimo naći
oko ishodišta polumjera r.
Želimo naći 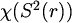 , tj. najmanji broj boja potreban za bojenje sfere takvo
da istobojne točke ne budu udaljene za 1.
(Pritom udaljenosti mjerimo euklidski, tj. onako kako ih računamo u
, tj. najmanji broj boja potreban za bojenje sfere takvo
da istobojne točke ne budu udaljene za 1.
(Pritom udaljenosti mjerimo euklidski, tj. onako kako ih računamo u 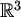 .)
Kako r raste, zakrivljenost sfere
.)
Kako r raste, zakrivljenost sfere 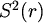 sve je manja pa je ona lokalno sve sličnija ravnini.
Zato s pravom očekujemo da će se to odraziti i na njezin kromatski broj.
sve je manja pa je ona lokalno sve sličnija ravnini.
Zato s pravom očekujemo da će se to odraziti i na njezin kromatski broj.
Jedino što je poznato o kromatskim brojevima sfera jest sljedeća tablica [GR].
U nju se uklapa i osnovni rezultat za ravninu ako je shvatimo kao sferu polumjera
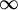 .
.
| polumjer sfere | donja ograda | gornja ograda |
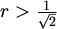
|
4 | 7 |
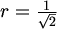
|
4 | 4 |
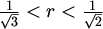
|
4 | 7 |
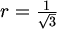
|
4 | 5 |
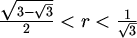
|
3 | 5 |
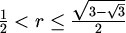
|
3 | 4 |
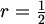
|
2 | 2 |
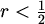
|
1 | 1 |
Uočimo da je sfera 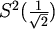 jedini netrivijalni slučaj iz gornje tablice
za koji je poznat kromatski broj,
jedini netrivijalni slučaj iz gornje tablice
za koji je poznat kromatski broj, 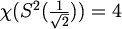 .
Definirat ćemo jedno njezino pravilno bojenje u 4 boje.
U tu svrhu koristit ćemo sferne koordinate. Svaka točka sfere određena je dvama kutovima:
.
Definirat ćemo jedno njezino pravilno bojenje u 4 boje.
U tu svrhu koristit ćemo sferne koordinate. Svaka točka sfere određena je dvama kutovima:
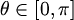 je kut između pozitivnog dijela
z-osi i spojnice te točke s ishodištem;
je kut između pozitivnog dijela
z-osi i spojnice te točke s ishodištem;
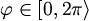 je kut između pozitivnog dijela
x-osi i projekcije te spojnice na xy-ravninu.
je kut između pozitivnog dijela
x-osi i projekcije te spojnice na xy-ravninu.
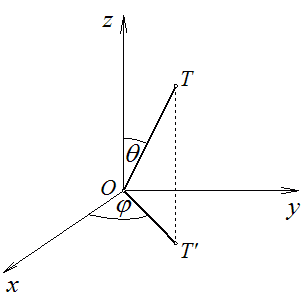
Primijetimo da su točke A i B na 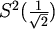 udaljene za 1
ako i samo ako je kut
udaljene za 1
ako i samo ako je kut 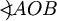 pravi.
Točke od
pravi.
Točke od 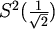 bojimo na sljedeći način:
bojimo na sljedeći način:
- Točke za koje je
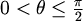 ,
,
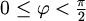 obojimo zeleno.
obojimo zeleno.
- Točke za koje je
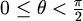 ,
,
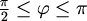 obojimo crveno.
obojimo crveno.
- Točke za koje je
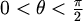 ,
,
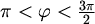 obojimo žuto.
obojimo žuto.
- Točke za koje je
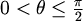 ,
,
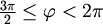 obojimo plavo.
obojimo plavo.
- Sve ostale točke obojimo kao njima antipodne (centralno simetrične s obzirom na ishodište).
Dakle, gornja polusfera sada izgleda ovako (gledana odozgo):
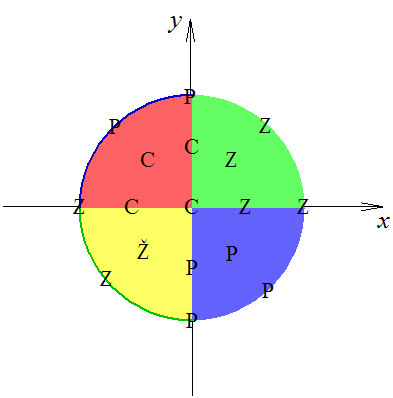
Čitatelj može sam lako provjeriti da je ovo bojenje dobro, iz čega proizlazi
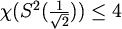 .
Začudno, obratnu nejednakost nešto je teže dokazati [Svo].
Jedna evidentna poteškoća je to što
.
Začudno, obratnu nejednakost nešto je teže dokazati [Svo].
Jedna evidentna poteškoća je to što 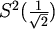 nema podgraf
"izomorfan" Moserovom vretenu. Neka čitatelj sam zaključi zašto!
nema podgraf
"izomorfan" Moserovom vretenu. Neka čitatelj sam zaključi zašto!
9. Bojenje metričkog prostora
Razmatranja iz prethodnih točaka prirodno nas vode do sljedećeg poopćenja.
Za bilo koji
metrički prostor
X=(X,d) možemo definirati
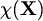 kao najmanji broj boja potreban za bojenje
skupa X takvo da ne postoje istobojne točke
kao najmanji broj boja potreban za bojenje
skupa X takvo da ne postoje istobojne točke
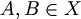 za koje bi vrijedilo
za koje bi vrijedilo 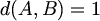 .
Vidjeli smo da određivanje
.
Vidjeli smo da određivanje 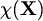 može biti vrlo težak problem.
Na ovom (prevelikom) nivou općenitosti zapravo i nema korisnih rezultata
osim de Bruijn-Erdösevog teorema.
može biti vrlo težak problem.
Na ovom (prevelikom) nivou općenitosti zapravo i nema korisnih rezultata
osim de Bruijn-Erdösevog teorema.
S druge strane, u pojedinim metričkim prostorima X broj
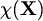 vrlo je lako odrediti.
Naprimjer, neka je opet X=
vrlo je lako odrediti.
Naprimjer, neka je opet X=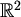 ,
ali sada uobičajenu euklidsku metriku
,
ali sada uobičajenu euklidsku metriku
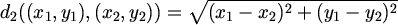 ,
, 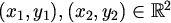
zamijenimo metrikom
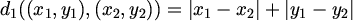 ,
, 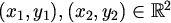 .
.
Nije teško vidjeti da je 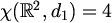 .
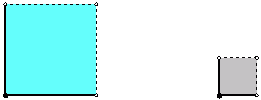
Jedno pravilno 4-bojenje izgleda ovako:
.
Jedno pravilno 4-bojenje izgleda ovako:

Označene točke elementi su cjelobrojne rešetke 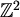 .
Od rubnih točaka kvadratima pripadaju dvije stranice i jedan vrh:
.
Od rubnih točaka kvadratima pripadaju dvije stranice i jedan vrh:
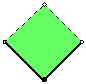
S druge strane, svake dvije od točaka
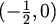 ,
, 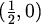 ,
,
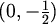 ,
, 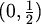 međusobno su udaljene za 1 (u metrici
međusobno su udaljene za 1 (u metrici 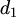 )
pa te točke moraju imati 4 različite boje.
Prema tome,
)
pa te točke moraju imati 4 različite boje.
Prema tome, 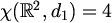 .
.
10. Umjesto zaključka
Ovo je bio pregled najzanimljivijih rezultata u vezi sa starim Nelsonovim problemom, ali smo uspjeli dotaknuti i problematiku nekoliko aktualnih matematičkih disciplina. Jednostavnije rezultate popratili smo dokazima, a za one složenije to bi bilo gotovo neizvedivo zbog mnogobrojnih novih koncepata i pojmova, a ozbiljno ograničenje je i razumna duljina članka. Zainteresirani čitatelj možda će poželjeti podrobnije proučiti neke aspekte problema pa se svi radovi korišteni prilikom pisanja ovog članka nalaze u opsežnom popisu literature.
Tko zna hoće li originalni Nelsonov problem ikada biti riješen?! Polustoljetni pokušaji njegovog rješavanja ne trebaju djelovati obeshrabrujuće: danas se znamo nositi s mnogim sličnim problemima (usp. točke 6, 7, 8 i 9). Možda nam nedostaje samo jedna maštovita dosjetka, a možda je ipak "poteškoća" u aksiomima teorije skupova ili čak temeljima matematičke logike. Kako god bilo, većina matematičara složit će se da samo rješenje problema nije uvijek najvažnije jer, prema riječima slavnog matematičara i filozofa Bertranda Russella, matematika ne posjeduje samo istinu, već i vrhunsku ljepotu.
Literatura
[BE] N.G. de Bruijn, P.Erdös,
A colour problem for infinite graphs and a problem in the theory of relations,
Nederl. Akad. Wetensch. Indag. Math., 13 (1951) 371-373.
[Cou] David Coulson,
A 15-colouring of 3-space omitting distance one,
Discrete Mathematics, 256 (2002), 83-90.
[DMR] E.D.Demaine, J.S.B.Mitchell, J.O'Rourke,
The Open Problems Project,
http://maven.smith.edu/~orourke/TOPP/P57.html#Problem.57
[Epp] D.Eppstein,
The Geometry Junkyard,
http://www.ics.uci.edu/~eppstein/junkyard/open.html
[Erd] P.Erdös,
On the combinatorial problems which I would most like to see solved,
Combinatorica, 1 (1981), 25-42.
[Fal] K.J.Falconer,
The realization of distances in measurable subsets covering
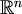 ,
,
Journal of Combinatorial Theory, A 31 (1981), 184-189.
[FW] P.Frankl, R.M.Wilson,
Intersection theorems with geometric consequences,
Combinatorica, 1 (1981), 357-368.
[Gar] M.Gardner,
Mathematical Games,
Scientific American, 203 (1960), 180.
[GR] J.E.Goodman, J.O'Rourke (editors), Handbook of Discrete and Computational Geometry, CRC Press LLC, 1997.
[Hoch] R.Hochberg,
Open Problems for Undergraduates - Graph Theory Open Problems,
http://dimacs.rutgers.edu/~hochberg/undopen/graphtheory/graphtheory.html
[HS] I.Hoffman, A.Soifer,
Another six-coloring of the plane,
Discrete Mathematics, 150 (1996), 427-429.
[Nech] O.Nechushtan,
On the space chromatic number,
Discrete Mathematics, 256 (2002), 499-507.
[Pegg] E.Pegg,
MathPuzzle - The Chromatic Number of the Plane,
http://www.mathpuzzle.com/chrompln.html
[Pla] PlanetMath Encyclopedia - Chromatic number of a space,
http://planetmath.org/encyclopedia/ChromaticNumberOfASpace.html
[Soi1] A.Soifer,
A six-coloring of the plane,
Journal of Combinatorial Theory, A 61 (1992), 292-294.
[Soi2] A.Soifer,
Chromatic number of the plane: Its Past and Future,
http://www.math.princeton.edu/~bsudakov/soifer2003.pdf
[SS] S.Shelah, A.Soifer,
Axiom of choice and chromatic number of the plane,
Journal of Combinatorial Theory, A 103 (2003), 387-391.
http://www.uccs.edu/~asoifer/
[Svo] K.Svozil,
The chromatic number of a sphere. Solution of problem nr. 10769,
The American Mathematical Monthly, 108 (2001), 774-775.
http://tph.tuwien.ac.at/~svozil/publ/blatter.htm
[Sze] L.A.Szekely,
Erdös on unit distances and the Szemeredi-Trotter theorems,
http://www.math.sc.edu/~szekely/erdoson1.pdf
[Vuk] M.Vuković, Matematička logika 1 (skripta), PMF-Matematički odjel, Zagreb, 2000.
[Wiki] Wikipedia, the free encyclopedia,
http://en.wikipedia.org/wiki/Wikipedia
[Wood] D.R.Woodall,
Distances Realized by Sets Covering the Plane,
Journal of Combinatorial Theory, A 14 (1973), 187-200.
1. Uvod
2. Formulacija problema i osnovni rezultati
3. Pokušaji popravljanja donje ograde
4. Pokušaji popravljanja gornje ograde
5. Veza s teorijom grafova i logikom sudova
6. Bojenje racionalnih točaka
7. Pravac, ravnina, 3D-prostor ...
8. Je li lakše obojiti sferu?
9. Bojenje metričkog prostora
10. Umjesto zaključka
Literatura