TV-matematika

Broj 3
	Dubravka Glasnović Gracin
	TV-matematika

	Sadržaj: Uvod "TV, 37 cm, prodajem..." Dijagonala ekrana Duljine stranica ekrana Widescreen televizori Geometrijsko rješenje Povijesni podaci Mjerne jedinice za veličinu ekrana Prednosti i mane widescreen-a Radni materijal za učenike Literatura Uvod Učenicima osnovnih i srednjih škola, kao i mnogim studentima, matematika često izgleda neprimjenjiva u svakodnevnom životu. Evo jednog primjera gdje se iza bezazlenog novinskog oglasa kriju osnovni matematički poučci. Valja naglasiti da je prvobitna "radna" verzija ovog članka namijenjena osnovnoškolskoj matematici i primjeni Pitagorinog poučka u svakodnevnom životu. Stoga je matematički jezik i gradivo ovog članka napisano tako da bude razumljivo i učeniku osmog razreda osnovne škole. Uz brojne konkretne činjenice vezane uz omjere stranica TV-ekrana, matematičko gradivo se nametnulo kao imperativ koji se mora znati želi li se u potpunosti snaći u kupovini televizora. Na kraju članka nalazi se download radna verzija za rad u razredu. "TV, 37 cm, prodajem..." Pogledamo li male oglase u bilo kojem od naših oglasnika, situacija će biti otprilike ovakva: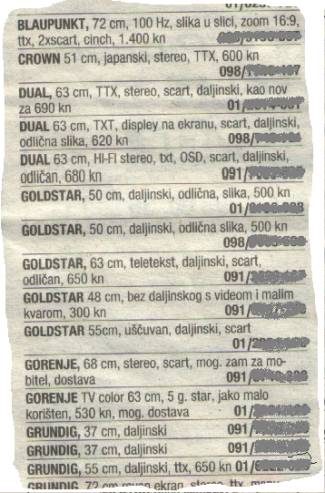 Uz osnovne značajke televizora koji prodaje prodavač uvijek daje i podatak o veličini televizora, uglavnom izražen u cm. Pogledajmo primjerice ovaj kratki oglas: U oglasu čitamo: "Grundig, 37 cm, daljinski". Iz ovih šturih podataka kupac bi trebao saznati dimenzije televizora. Pitamo se je li to zaista moguće. Jedini podatak koji je naveden izvjesna je duljina od 37 cm. Pitanje je o kojoj se veličini radi. Radi li se o visini kutije televizora, dubini kutije, širini kutije, visini ekrana, dijagonali ekrana, širini ekrana ili nekom drugom podatku? visina kutije televizora dubina kutije televizora visina ekrana dijagonala ekrana širina ekrana Dijagonala ekrana Veličina ekrana koja je navedena u oglasu standardiziran je podatak, a odnosi se na duljinu dijagonale klasičnog ekrana televizora. Tako u oglasima nailazimo na klasične televizore s duljinama dijagonala 50 cm, 37 cm, 51 cm, 67 cm itd. Kako se veličina ekrana televizora izražava duljinom njegove dijagonale, zapitajmo se može li se samo na temelju duljine dijagonale ekrana jednoznačno odrediti njegova širina i visina. Kolike su dimenzije ekrana (širina, visina) televizora kojem je dijagonala duga 37 cm? Prisjetimo li se Talesovog poučka o obodnom kutu, zaključit ćemo da ima beskonačno mnogo različitih pravokutnih ekrana kojima je dijagonala duga 37 cm. 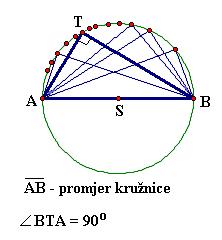Talesov poučak (o kutu nad promjerom): Svaki obodni kut nad promjerom kružnice je pravi kut. Dakle, po Talesovom poučku, nacrtamo li dužinu AB i na njoj konstruiramo kružnicu k kojoj je AB dijametar, tada je svaki trokut ABT pravokutan, pri čemu je T neka točka s kružnice k. Trokuta ABT ima koliko i točaka na kružnici k, tj. beskonačno mnogo. Preslikamo li centralnom simetrijom točku T obzirom na središte kružnice kao središte simetrije, dobit ćemo točku V i pravokutnik AVBT s dijagonalom AB: Kako smo pravokutnik AVBT dobili centralnom simetrijom iz trokuta ABT, zaključujemo da i pravokutnika kojima je duljina dijagonale \|AB\| ima beskonačno mnogo. 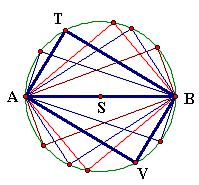Animacija - svi pravokutnici s konstantnom dijagonalom Svi pravokutnici sa slike imaju dijagonalu iste duljine. Dakle, ako nam je u oglasniku zadana samo dijagonala televizora od 37 cm, ekrana s takvom dijagonalom ima beskonačno mnogo. Zaključujemo da duljina dijagonale nije dovoljan podatak za definiranje jednog ekrana televizora, već da nam nedostaje još podataka. Zapravo, nedostaje nam još samo jedan podatak, a to je omjer duljina stranica svakog ekrana. Pogledamo li donje dvije slike gdje je Talesov poučak nacrtan na stvarnom televizoru, primijetit ćemo da točka T nije bilo koja točka kružnice, već je to pomno odabrana točka na kružnici kako bi ekran dobio svoj uobičajeni oblik. Točka T na kružnici odabrana je tako da vrijedi \|TB\| : \|TA\| = 4 : 3. 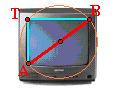Omjer duljina stranica ekrana svakog televizora poznat je i standardiziran u cijelom svijetu: Duljine susjednih stranica svakog klasičnog ekrana odnose se kao 4:3. To je podatak koji nije naveden u oglasu jer se on podrazumijeva pa je dovoljno navesti samo duljinu dijagonale. 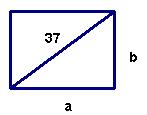Duljine stranica ekrana Sada možemo izračunati duljine stranica ekrana uz zadanu duljinu dijagonale. Pravokutnik sa slike predstavljat će naš ekran: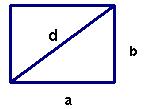 Kako se duljine stranica ekrana klasičnog televizora odnose kao 4:3, vrijedi da je a = b. Primjećujemo pravokutan trokut kojem je hipotenuza dijagonala pravokutnika d, a katete su stranice ekrana duljine i b. Primjenom Pitagorinog poučka rješavamo zadatak: Pronašli smo vezu između duljina dijagonale i kateta trokuta: a = 4/5 d, b = 3/5 d. 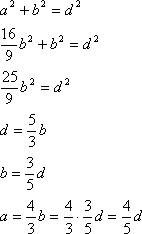Pomoću ovih formula možemo izračunati dimenzije svakog klasičnog ekrana iz oglasa. Stoga pronađimo duljinu i širinu ekrana iz oglasa s početka teksta: Dijagonala ekrana duga je 37 cm. Stranice pravokutnika (ekrana) označimo s a i b. Računanjem po Pitagorinom poučku ili pak uvrštavanjem u gore dobivene formule , , dobivamo da su stranice ekrana iz oglasa duge 29.6 cm i 22.2 cm. 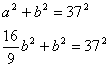No, krenimo i korak dalje. Po preporukama, daljina iz koje gledamo televizor trebala bi biti najmanje 3 puta veća od duljine dijagonale ekrana. Izračunajmo stoga koliko bi trebalo udaljiti trosjed od televizora iz oglasnika. Kako je dijagonala ekrana zadanog televizora 37 cm, a preporučena udaljenost s koje se gleda jednaka trostrukoj dijagonali, znači da bismo trosjed trebali udaljiti od televizora barem 1,11 m. Widescreen televizori Do sada su u tekstu spominjani "klasični" televizori. Klasičnim televizorima nazivaju se televizori kojima se stranice ekrana odnose u omjeru 4:3. Osim te vrste ekrana danas se izrađuju i vrlo su popularni tzv. widescreen televizori (eng. wide screen = širok ekran), kojima se susjedne stranice odnose u omjeru 16:9. Kao i kod klasičnog omjera, možemo izračunati duljine stranica ekrana uz zadanu duljinu dijagonale širokog ekrana. 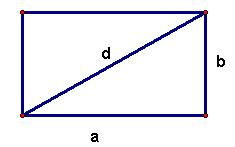Pravokutnik sa slike predstavljat će naš ekran: Kako se stranice ekrana widescreen televizora nalaze u omjeru 16:9, vrijedi da je a = b. Primjenom Pitagorinog poučka rješavamo zadatak: Pronašli smo vezu između duljina dijagonale i kateta trokuta: , . 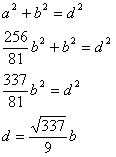Pomoću ovih formula možemo izračunati dimenzije svakog širokog ekrana iz oglasa kojem je zadana samo duljina dijagonale. Geometrijsko rješenje Dva ili više mnogokuta slična su ako su im odgovarajući kutovi jednaki i odgovarajuće stranice proporcionalne. Kako su svi kutovi pravokutnika pravi kutovi, da bi dva pravokutnika bila slična dovoljno je da im stranice budu proporcionalne. A kako su stranice svih klasičnih ekrana u omjeru 4:3, zaključujemo da su ekrani svih klasičnih televizora međusobno slični. Ovi zaključci o sličnosti pomoći će nam da zadani oglas iz novina prikažemo i u geometrijskom svjetlu. Zadatak 1: Konstruiraj pravokutnik ABCD, \|AB\| = a, kojem je omjer duljina susjednih stranica 4:3. Rješenje: Nacrtajmo neku dužinu \|AB\| = a. Kako duljine susjednih stranica pravokutnika trebaju biti u omjeru 4:3, to znači da je \|AB\| : \|BC\| = 4 : 3, te da je \|BC\| = 3/4 a. Dužinu AB podijelimo simetralama na 4 jednaka dijela i pronađemo 3/4 njene duljine. Zatim konstruiramo pravi kut iz vrha B i na okomit krak nanesemo . Točku D dobivamo iz svojstva da su nasuprotne stranice pravokutnika jednakih duljina. 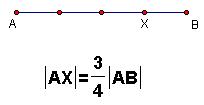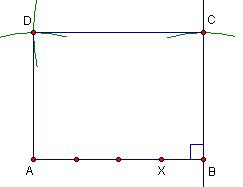Zadatak 2: Konstruiraj pravokutnik kojem je omjer susjednih stranica 16:9. Rješenje: Neka je BC stranica traženog pravokutnika ABCD. Zadatak se rješava slično kao u prethodnom zadatku, dijeljenjem dužine BC na jednake dijelove i traženjem . U prethodna dva poglavlja računski smo pronašli kako izračunati duljine stranica pravokutnika kojem je zadana dijagonala i omjer susjednih stranica 4:3 za klasičan, odnosno 16:9 za widescreen televizor. Pronađimo i geometrijsko rješenje ovog zadatka: Zadatak 3: Zadana je dužina duljine d. Konstruiraj pravokutnik ABCD* kojem je dijagonala duljine d, a omjer duljina susjednih stranica je 4:3.* Rješenje: 1. 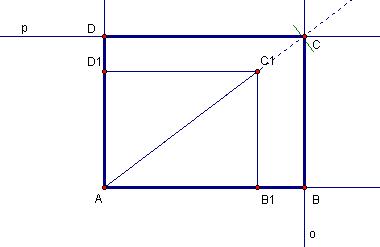način: Riješit ćemo ovaj zadatak korištenjem sličnosti pravokutnika. Konstruirajmo pravokutnik AB₁C₁D₁ sa stranicama duljina 4 cm i 3 cm. To nije pravokutnik koji se traži u zadatku, ali za njega vrijedi da su mu stranice u omjeru 4:3 (mogli smo nacrtati i bilo koji drugi pravokutnik sa stranicama u omjeru 4:3). To znači da je on sličan traženom pravokutniku ABCD. Istaknimo jednu njegovu dijagonalu, npr. . Budući da su pravokutnici slični, odgovarajuće stranice su im proporcionalne. No, tada su im i duljine dijagonala d i d₁ proporcionalne s istim koeficijentom proporcionalnosti. Na polupravac AC₁ iz početne točke A nanesemo zadanu duljinu dijagonale d. Kako su pravokutnici slični, dobit ćemo točku C, tj. $k(A,d) presjek AC_1 = {C}$ . 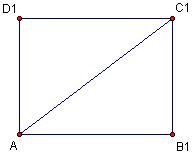Sada je lako konstruirati pravokutnik ABCD. Potrebno je konstruirati okomice o i p iz točke C na pravce AB₁ i AD₁. 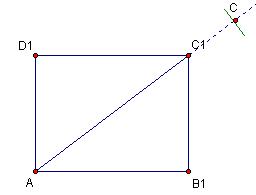Tada je $o presjek AB_1 = {B}$ i $p presjek AD_1 = {D}$ . Konstrukcija je gotova spajanjem točaka A, B, C i D u pravokutnik. 2. način: U prethodnom poglavlju računskim smo putem dobili da za omjere stranica 4:3 i zadanu duljinu dijagonale d vrijedi da je , , pri čemu su a i b duljine susjednih stranica zadanog pravokutnika. Rješenje možemo naći dijeljenjem dužine na jednake dijelove. Nacrtajmo dužinu AC duljine d i podijelimo je na 5 jednakih dijelova. Tri petine dužine AC bit će jednake duljini stranice b, a četiri petine bit će jednake duljini stranice a. Nađimo točku M na dužini AC takvu da je \|AM\| = b = 3/5 d. Primijenimo na ovaj crtež Talesov poučak: Konstruirajmo kružnicu k sa središtem S kojoj je AC dijametar. Primijetimo da je \|AM\| = b = \|AD\| = \|CB\|. Stoga je . 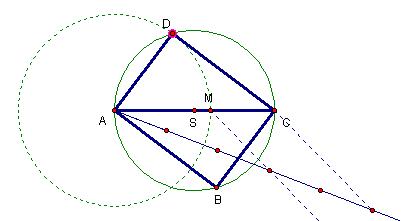Točku B dobivamo na isti način, ili pak centralnom simetrijom točke D obzirom na središte S. Tako dolazimo do pravokutnika ABCD. Naravno, na isti način možemo zaključiti da su widescreen ekrani međusobno slični, te geometrijski riješiti sljedeći zadatak. Zadatak 4 Zadana je dužina duljine d. Konstruiraj pravokutnik ABCD* kojem je dijagonala duljine d, a omjer duljina susjednih stranica je 16:9.* Povijesni podaci Pogledamo li slike klasičnog i widescreen ekrana, primjećujemo da je widescreen ekran "izduženiji" od klasičnog. Također primjećujemo da je omjer stranica 16:9 širokog ekrana kvadrat klasičnog omjera 4:3. Animacija - od klasičnog do širokog ekrana Pitamo se jesu li izduženiji oblik i kvadratni omjer slučajni. Odgovor ćemo pronaći vratimo li se više od 100 godina unatrag u povijest. Prvobitan omjer stranica 4:3 definiran je još davne 1889. godine u laboratoriju Thomasa A. Edisona kada je znanstvenik W.K.L. Dickson eksperimentirao s filmskim uređajem zvanim kinetoskop. Za njega je, prvenstveno zbog štednje skupe filmske vrpce, napravio film sa sličicama 1'' (inč) širine i 3/4'' (inča) visine. Taj omjer stranica svake sličice na filmu postala je standardna veličina za filmske kamere, a time i za ekrane na koje su se projicirali filmovi te konačno i za cijelu filmsku industriju. Godine 1941., kada su se određivali standardi za televizijska emitiranja donesen je standard da će ekran svakog televizora imati omjer stranica 4:3, u skladu s cijelom filmskom industrijom. Tako su se filmovi, koji su do pojave televizora bili dostupni samo u kinima, mogli gledati na televizoru iz kućnog naslonjača i odlazak u kino bio je sve rjeđi. Ponekad se umjesto omjera 4:3 govori o omjeru 1.33:1. Filmovi prije 50-tih snimali su se dakle u formatu 1.33:1. To su, primjerice, filmovi Drakula (1931.), Prohujalo s vihorom (1939.), Divan život (1946.), Čarobnjak iz Oza (1939.) kadrove kojih vidimo na slikama, te mnogi drugi. Pedesetih godina filmski Hollywood osjetio je lošiju zaradu zbog pojave televizora pa je trebalo smisliti marketinšku kampanju kako bi se gledaoce opet privuklo u kina. Pokušali su s mnogim idejama, nekim boljim, nekim lošijima, ali uspješni pokušaj (koji osjećamo i danas) bila je promjena formata filma i filmskog platna. Širi ekrani garantirali su publici izraženiji doživljaj onoga što se događa na filmu. To je bila vrlo jednostavna, ali odlična ideja za vraćanje publike u kina. A kako naše oko prima širu sliku od ekrana omjera 4:3, širi ekran ima opravdanje i zbog tog razloga. Tako se filmovi već više od 50 godina snimaju (i gledaju u kinu) u široj verziji, dok su dimenzije ekrana televizora ostale do danas iste, tj. u omjeru 4:3. Tek nedavno je televizijska industrija počela proizvoditi televizore koji bi bili kompatibilni s filmovima koji se prikazuju, tzv. widescreen televizore. Tako je format ekrana više prilagođen slici koju naše oko gleda, budući da je naše vidno polje «više pravokutnog nego kvadratičnog» oblika. Time je naš vizualni doživljaj izraženiji. Spomenimo još i to da se filmovi ne snimaju točno s omjerom slike 16:9 (to je omjer stranica filmskog platna i televizora), već svaka kompanija ima svoj format filma, koji više ili manje odstupa od widescreen omjera. Najrašireniji su formati 1.85:1 i 2.35:1, a spomenimo i 2.22:1 te 1.651. U formatu 1.85:1 snimani su npr. Engleski pacijent (na slici dolje lijevo), Svi predsjednikovi ljudi, Ptice itd. U formatu 2.35:1 snimani su npr. Ratovi zvijezda, Tanka crvena linija (na slici dolje desno), Apokalipsa danas itd. Nakon desetljeća eksperimentiranja s omjerima koji bi bili najprimjereniji našem vidnom polju, filmska industrija opredijelila se za omjer filmskog platna 16:9 u kinima. Ponekad se umjesto omjera 16:9 govori o omjeru 1.78:1. Omjer 16:9 je i izvjesni kompromis između svih filmskih formata jer je trebalo načiniti filmsko platno koje će jednako efektno prikazivati sve filmske formate. Po uzoru na filmska platna, dogovoreno je i da će svaki widescreen televizor imati ekran s omjerom stranica 16:9. Mjerne jedinice za veličinu ekrana U Europi se duljina dijagonale ekrana izražava u centimetrima, a u Velikoj Britaniji i SAD-u u inčima (oznaka: ''). Inč (eng. inch) je jedinica za duljinu i jedan inč iznosi 2.54 cm. Veličina svakog kompjutorskog monitora prikazuje se također pomoću njegove dijagonale, no uvijek izražene u inčima, i u Europi. Tako danas najčešće nailazimo na 15-inčne, 17-inčne i 19-inčne monitore, sve s omjerom stranica 4:3. Iako se dijagonala televizora u Hrvatskoj izražava u cm, kod nekih naših distributera velikih proizvođača televizora mogu se naći podaci s dijagonalom izraženom u inčima. Ovaj aplet pretvara inče u centimetre i obratno. Prednosti i mane widescreen-a U Povijesnim podacima naveli smo da se filmovi već više od 50 godina snimaju i prikazuju u kinima u widescreen formatima, no televizori su praktički do danas ostali na klasičnom omjeru 4:3. Pitamo se što se, dakle, događa sa slikom snimljenom u širokom formatu kada se emitira na klasičnom televizoru. Jedno rješenje ove nekompatibilnosti je tzv. letterboxing, tj. slika se suzi i da njezini se krajevi malo "odrežu". Tako se, primjerice, kada gledamo filmove na klasičnom televizoru, mogu pojaviti dvije crne pruge iznad i ispod slike, a izvorni materijal će se proporcionalno suziti. Zadatak 5: Na klasičnom ekranu možemo gledati film widescreen formata, tako da u ostatku ekrana iznad i ispod widescreena budu crne pruge kao na slici gore. Koliki dio klasičnog ekrana ostaje neiskorišten pojavom crnih pruga? Rješenje: Duljinu vodoravne stranice ekrana označimo s a. Tada će duljina okomite stranice biti . Vodoravna stranica slike ima duljinu a, a okomita ima duljinu 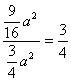. Površina cijelog ekrana je tada , a površina njegovog iskorištenog dijela je . To znači da je iskorišteno: = 75% ekrana. Dakle, ostala je neiskorištena 1/4, tj. 25% klasičnog ekrana. Zadatak 6: Pogledajmo problem letterboxinga i s geometrijskog aspekta. Unutar pravokutnika ABCD koji prikazuje klasičan ekran treba konstruirati pravokutnik EFGH widescreen formata kao na slici, tako da pravokutnici ABFE i HGCD budu sukladni. 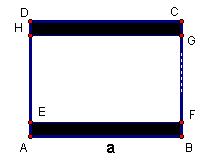Rješenje: Konstruirajmo pravokutnik ABCD s omjerom duljina stranica \|AB\| : \|BC\| = 4 : 3. Ako duljinu stranice AB označimo s a, tada će biti 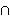, , . Dijeljenjem dužine AB na polovine, četvrtine, osmine i konačno šesnaestine brzo možemo konstruktivno dobiti veličinu . (Još brže nađemo li 3/4 od dužine .) To je duljina tražene dužine FG koju još treba smjestiti "na sredinu" dužine BC. Nacrtajmo pomoćnu dužinu . Pronađimo polovište P dužine AD, te polovište M dužine XY. Tada je: k(P, \|XM\|) AD = {E, H}. Vratimo se na drugi način prikazivanja širokog filma na klasičnom ekranu. Još jedan način je rezanje filma tako da se prikaže samo najvažniji dio kadra. Ta se tehnika naziva "pan-scan" tehnika i izvode je tehničari u studijima. Ako pažljivije pratimo sam početak nekog hollywoodskog filma, prije početka emitiranja na ekranu se nekad može vidjeti mala poruka koja glasi: This film has been modified from its original version. It has been formatted to fit your screen. U prijevodu: "Ovaj film je promijenjen u odnosu na svoju originalnu verziju. Formatiran je prema dimenzijama Vašeg ekrana." Kada je studio pustio u prodaju verziju filma za male ekrane, morali su "odrezati" bočne strane filma kako bi dimenzije filma bile u skladu s televizijskim omjerom 4:3. Pogledajmo što se događa s filmovima snimljenima u formatu 2.35:1 kada se gledaju na ekranu 1.33:1. Dobar primjer za to dat će nam dva kadra iz filma "Malo dobrih ljudi" s Tomom Cruiseom, Demi Moore i Jackom Nicholsonom u glavnim ulogama, snimanog u formatu 2.35:1. Primijetimo koliki su dijelovi slike izrezani. Zaključujemo da je velik dio kadra izrezan, što smanjuje doživljaj, umjetničku dimenziju filma i zakida ono što je redatelj želio reći. Izračunajmo za koliko smo "zakinuti" što se veličine kadra tiče. Zadatak 7: Film "Malo dobrih ljudi" snimljen je u formatu 2.35:1. Za potrebe emitiranja na malim ekranima film je izrezan za format 4:3. a) Procijeni, gledajući gornje primjere, koliki je dio filma odrezan. Je li to, po tvojoj procjeni, više ili manje od polovice originalne sličice? b) Izračunaj koliki je postotak originalnog filma odrezan na svakoj sličici. Rješenje: a) Procjena je individualna, no svakako je jasno da se radi otprilike o polovici originalnog filma. Je li to točno pola, malo više ili malo manje, ovisi o individualnoj procjeni, a točnost svoje procjene provjerite u b) zadatku. b) Kako je originalan film sniman u formatu 2.35:1, stranice ekrana možemo označiti s 2.35a i a. Površina tog pravokutnika, tj. originalne sličice, tada je 2.35a². Na isti način zaključujemo da je površina izrezanog ekrana 1.33a². To je 56.6% originalne slike jer je p = 1.33a² : 2.35a² = 0.566, p = 56.6%. Kako od slike površine 2.35a² trebamo uzeti njenih 56.6%, zaključujemo da ćemo odbaciti 43.4% originalne slike. Zadatak 8: Izračunaj koliki se dio slike (u %) izbacuje kod prikazivanja filmova formata 1.85:1. Rješenje: Zadatak rješavamo na isti način kao prethodni. Površina originalne slike je 1.85a², a klasične 1.33a². To je 71.9% originalne široke slike. Zaključujemo da ćemo u ovom slučaju odbaciti 28.1% originalne slike. Zadatak 9: Legendarni film "Ben Hur" snimljen je u formatu 2.76:1. Izračunaj koliki se dio slike izbacuje primjenom ove tehnike. Rješenje: Riješimo li zadatak na isti način kao dva prethodna, dobit ćemo da se u tom filmu odbacuje 51.8% originala. Dakle, čak preko 50%. Zbog tog razloga ovaj se film uglavnom prikazuje u verziji s crnim prugama (letterboxing). Mnogi ljubitelji sedme umjetnosti često apeliraju na gledatelje da filmove, zbog umjetničke cjelovitosti, gledaju u originalnim formatima s crnim prugama i da ne kupuju video-kazete i DVD-e s osakaćenim pan-scan verzijama filmova. Razmatrali smo mogućnosti i probleme u slučaju da imamo klasičan televizor. Pogledajmo sada obrnutu situaciju. Ako imamo widescreen televizor, iz svega do sada napisanog zaključujemo da možemo uživati u vrhunskom filmskom doživljaju. Međutim, što ako je film koji gledamo snimljen prije 1950. ili želimo gledati neki TV-program koji nije snimljen filmskom kamerom? Danas se najveći dio svakodnevnog televizijskog programa emitira u klasičnom formatu. Tada se opet prilazi raznim više ili manje efikasnim metodama za rješenje ove nekompatibilnosti. Srećom, widescreen televizori su mahom suvremeni uređaji koji samim korisnicima nude mogućnost izbora za rješenje ovog problema. Na primjer, nudi se mogućnost gledanja klasične slike tako da se s lijeve i desne strane slike pojave dvije okomite crne pruge. Tako se izbjegava neproporcionalno razvlačenje slike. U slučaju da gledatelja smetaju crne pruge oko slike, moderni widescreen televizori mogu "rastegnuti" tu sliku na čitav ekran, povećati je ili čak neproporcionalno raširiti. Evo konkretnih rješenja kako ekran 16:9 modificirati za gledanje 4:3 slike: crnim prugama (1. slika), zumiranjem (2. slika), širenjem (3. slika) te širenjem i zumiranjem samo krajeva slike, dok sredina ostaje netaknuta (4. slika). Zadatak 10: Izračunaj koliki dio widescreen ekrana ostaje neiskorišten ako koristimo letterboxing (opciju s crnim prugama). Rješenje: Ako okomitu stranicu ekrana označimo s a, onda je vodoravna stranica duga . Duljina slike je tada . Izračunajmo koliki je dio widescreen ekrana iskorišten: = 75%. To znači da 25%, tj. 1/4, widescreen ekrana ostaje neiskorišteno u slučaju da na širokom ekranu gledamo emisije snimljene u klasičnom formatu. Zadatak 11: Konstruiraj pravokutnik s omjerom stranica 16:9, a zatim unutar njega konstruiraj pravokutnik s omjerom stranica 4:3 kao na gornjoj Slici 1. I na kraju, ako kupujete televizor, dobro je zapitati se koju vrstu programa najviše gledate. Ako većinom gledate TV-emisije, potražite klasičan televizor s omjerom 4:3 jer se većina TV programa snima u ovom formatu. Ukoliko više gledate filmove s DVD-a, svakako potražite oglase s widescreen ekranima 16:9 jer će doživljaj biti jači, a neće biti ni rezanja slike. A ponekad otiđite i u kino. Sretno! Radni materijal za učenike Download verzija za profesore matematike: nastava.pdf Literatura [1] B. Dakić: Matematika 7 Plus, Element, Zagreb, 2002. [2] L. Krnić, Z. Šikić: Matematika 7, Profil, Zagreb, 1998. [3] B. Pavković, D. Veljan: Elementarna matematika 1, Tehnička knjiga, Zagreb, 1992. [4] http://www.pbs.org/opb/crashcourse/aspect_ratio/ [5] http://www.flattvpeople.com/tutorials/aspect-ratios.asp [6] http://att.com.com/4520-6463_7-1016109-4.html [7] http://www.forster.hr/acatalog/kako_kupiti.html [8] http://www.reelclassics.com/Techtalk/panscan-article.htm Uvod "TV, 37 cm, prodajem..." Dijagonala ekrana Duljine stranica ekrana Widescreen televizori Geometrijsko rješenje Povijesni podaci Mjerne jedinice za veličinu ekrana Prednosti i mane widescreen-a Radni materijal za učenike Literatura