
Broj 6










Tvrtko Tadić
Matematika parnog stroja


Sadržaj:
1. Uvod2. Parni stroj
3. Wattov jednostavni linearizirajući mehanizam
4. Wattov drugi parni stroj
5. Još jedan pokušaj
6. Rješenje problema
7. Zaključak
8. GSP file
9. Literatura
1. Uvod
U ovom ćemo se članku upoznati s jednim od važnih problema prve industrijske revolucije. Pitanje je kako parni stroj učiniti učinkovitim. Ovdje ćemo se pozabaviti temom članka [2], u kojem su izneseni ti problemi. U cijeloj priči koristit ćemo računalni program The Geometer's Sketchpad. Cilj nam je razmotriti te probleme i pomoću software-a pokazati da su rezultati koje su dobili njihovi otkrivači ispravni. Na kraju će se problem svesti na pitanje pretvaranja kružnog gibanja u linearno i obrnuto.2. Parni stroj
1780-ih James Watt usavršio je parni stroj, ostalo je povijest. Međutim, kod parnog stroja bilo je mnogih problema s kojima se njegov izumitelj domišljato borio. Prvi parni stroj bio je oblika prikazanog na slici 1.
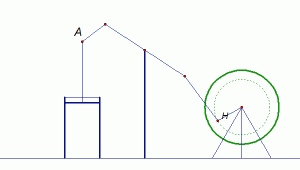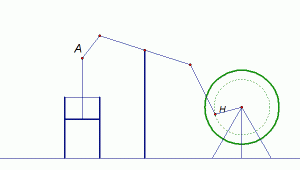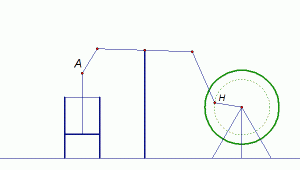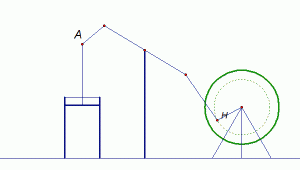 |
| Slika 1: Prvi parni stroj |
3. Wattov jednostavni linearizirajući mehanizam
Stoga je Watt počeo razmišljati mora li točka A nužno ići po pravcu. Watt se tada dosjetio sljedeće ideje (vidi sliku 2.). Neka su točke O1 i O2 nepomične. Neka se točke B i C miču oko O1 i O2 na jednakim udaljenostima od njih i neka je |BC| isto nepromjenjive vrijednosti. Watt je tada pretpostavio da će točka M, koja je polovište dužine BC, ležati na pravcu.
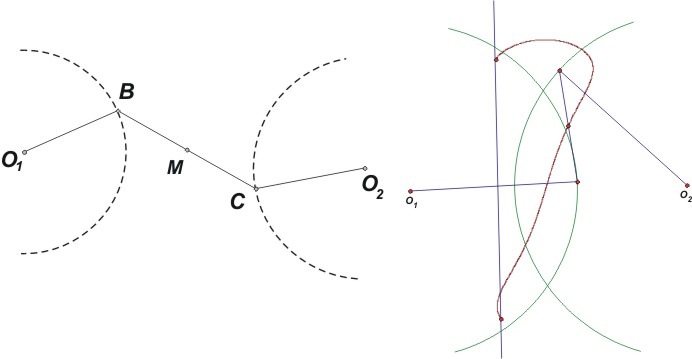 |
| Slika 2: Leži li točka M na pravcu? |
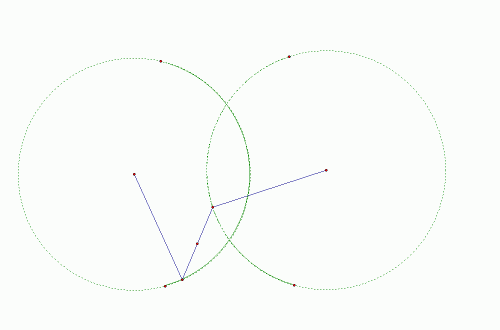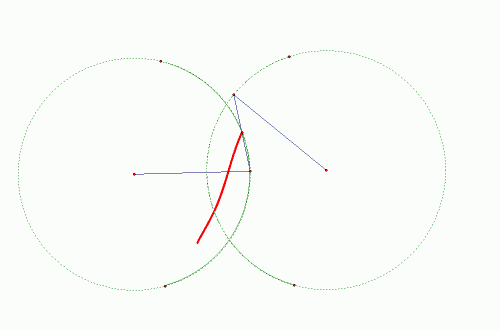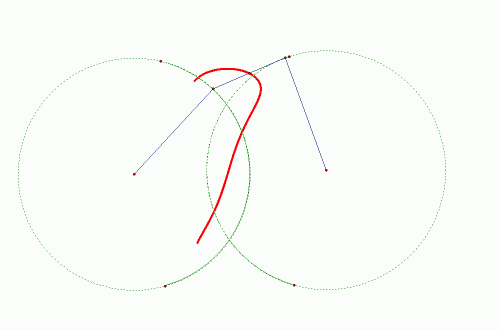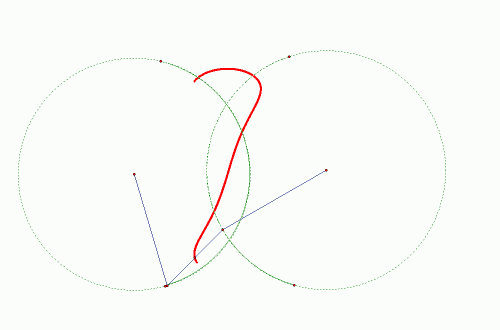 |
| Slika 3: Kretanje točke M |
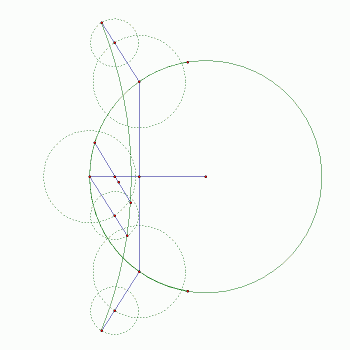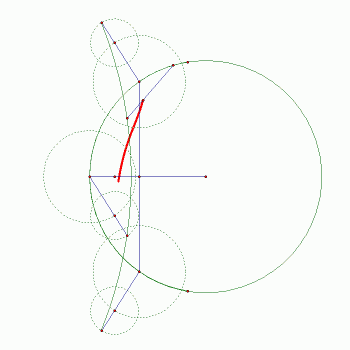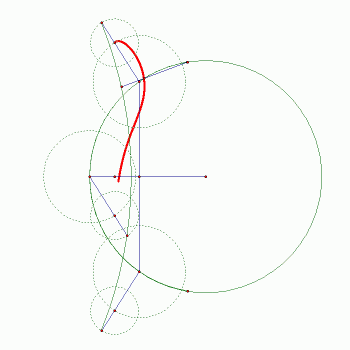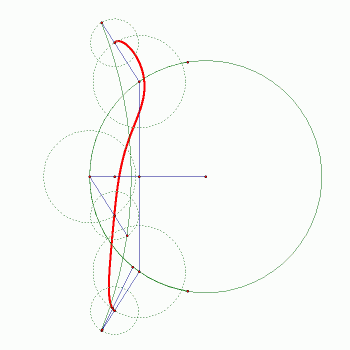 |
| Slika 4: Trajektorija i Wattova konstrukcija |
4. Wattov drugi parni stroj
Taj njegov pronalazak omogućio mu je da svoj stroj spoji čvršće i da mu se ne raspada. Tako je nastao Wattov drugi stroj koji je bio dovoljno stabilan za praktične potrebe. Sam Watt smatrao je ovo otkriće (približne krivulje) svojim najvećim znanstvenim postignućem. Pogledajmo sada kako je njegov stroj radio.
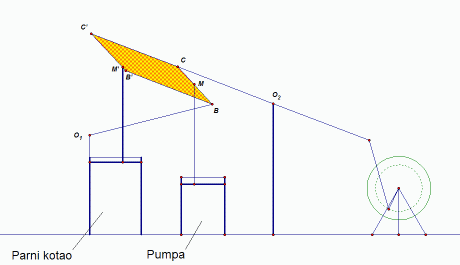 |
| Slika 5: Wattov drugi parni stroj |
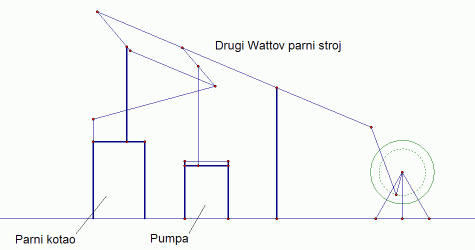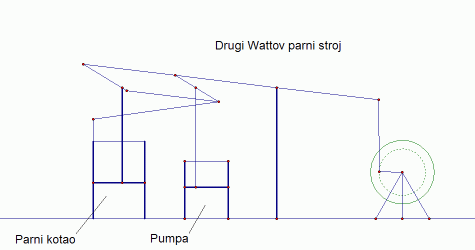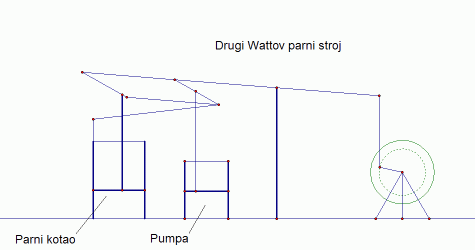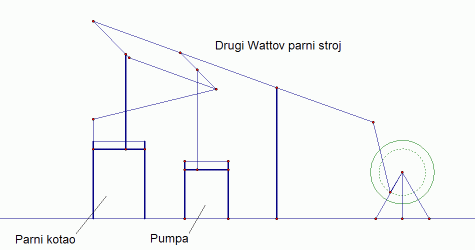 |
| Slika 5a: Wattov drugi parni stroj - animacija |
5. Još jedan pokušaj
Pokušaj da se riješi pitanje pretvaranja linearnog u kružno gibanje još će dugo mučiti znanstvenike. Ruski matematičar (i mehaničar) Čebišev istražujući funkcije koje imaju minimalnu devijaciju od nule ponudit će svoj mehanizam. Ovaj mehanizam će isto tako biti približno rješenje problema. Ovdje ćemo demonstrirati kako izgleda mehanizam - više o njemu možete vidjeti u članku [3].
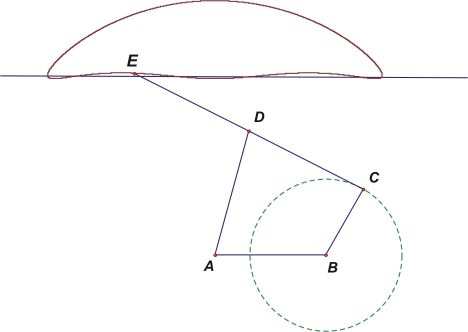 |
| Slika 6: Model Čebiševljevog linearizirajućeg mehanizma |
|ED| = |DC| = |AD| = a,
|BC| = b,
3|AB| = |DC| + |AD| +
|BC|.
Aplet - Model Čebiševljevog linearizirajućeg mehanizma
6. Rješenje problema
Nakon mnogih pokušaja, problem pretvaranja kružnog gibanja u linearno riješen je tek 1867. Skoro stoljeće kasnije! S obzirom da je riječ o problemu koji pravac mora preslikati u kružnicu i obrnuto, rješenje uključuje inverziju. Dok su nam prethodna rješenja nudila tek aproksiomacije pretvaranja linearnog u kružno gibanje (i obrnuto) ovo je prvo strogo (matematički gledano) rješenje tog problema. Rješenje je ponudio francuski inženjer Charles-Nicolas Peaucellier (1832.-1912.). Do istog otkrića došao je ruski matematičar Lippman Lipkin (živio u Rusiji i Latviji), nezavisno i nešto kasnije od Peaucelliera.
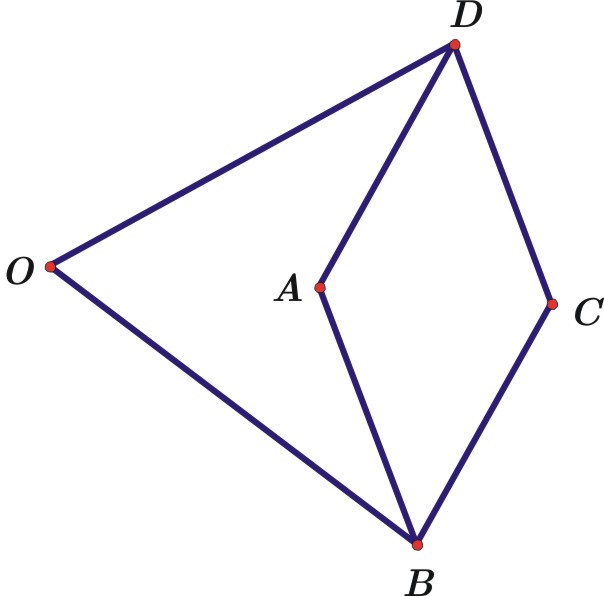 |
| Slika 7: Peaucellier-Lipkinov inverzor |
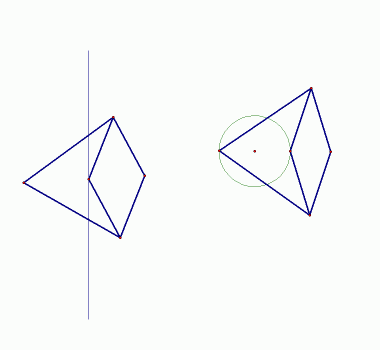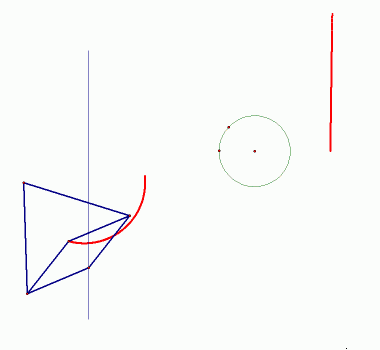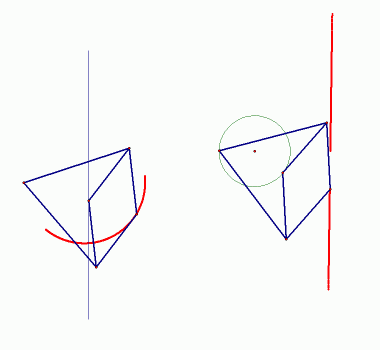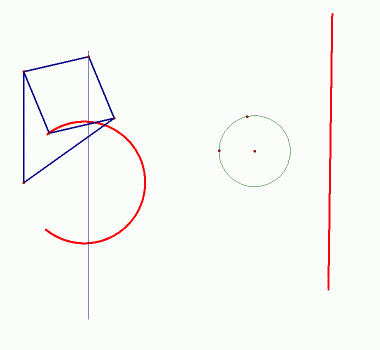 |
| Slika 8: Pojava inverzije |
7. Zaključak
Kako vidimo, program The Geometer's Sketchpad može biti jako koristan u izradi modela gibanja i raznih mehanizama. Ono za što je otkrivačima (,,pionirima znanosti'') trebalo mnogo mukotrpnog posla i papira, mi uz malu pomoć nove tehnologije možemo brzo i lako napraviti i provjeriti njihove rezultate, a oni su se morali bojati da negdje nisu pogriješili u računu.8. GSP file
Ovaj članak je dorađena verzija članka [4]. Ovdje je objavljen kako bi čitatelji mogli vidjeti animirane verzije slika i uzeti GSP file u kojima su one rađene.Ovdje možete preuzeti GSP file u kojem su izrađene slike.
9. Literatura
[1] Malkevitch J., Linkages: From Fingers to Robot Arms, What's New in Mathematics Feature Column Archive, AMS, 2002.[2] Solovyov Y., Making the crooked straight, Quantum the student magazine of math and science, vol 1. nr. 2, NSTA, Washington, 1990.
[3] Tadić T., Model Čebiševljevog linearizirajućeg mehanizma, PlayMath časopis V. gimnazije za matematiku i informatiku, broj 4, Zagreb, 2004.
[4] Tadić T., Matematika parnog stroja, Poučak časopis za metodiku i nastavu
matematike, broj 18-19, HMD i
Profil International, Zagreb, 2004.
[5] Home Page for Virtual Mechanisms,
Brock Institute for Advanced Studies, Roxbury
1. Uvod
2. Parni stroj
3. Wattov jednostavni linearizirajući mehanizam
4. Wattov drugi parni stroj
5. Još jedan pokušaj
6. Rješenje problema
7. Zaključak
8. GSP file
9. Literatura