Hrvatski matematički elektronski časopis math.e

http://www.math.hr/~mathe/

Matematika parnog stroja

Tvrtko Tadić

Sadržaj:

1. Uvod
2. Parni stroj
3. Wattov jednostavni linearizirajući mehanizam
4. Wattov drugi parni stroj
5. Još jedan pokušaj
6. Rješenje problema
7. Zaključak
8. GSP file
9. Literatura

1. Uvod

U ovom ćemo se članku upoznati s jednim od važnih problema prve industrijske revolucije. Pitanje je kako parni stroj učiniti učinkovitim. Ovdje ćemo se pozabaviti temom članka [2], u kojem su izneseni ti problemi. U cijeloj priči koristit ćemo računalni program The Geometer's Sketchpad. Cilj nam je razmotriti te probleme i pomoću software-a pokazati da su rezultati koje su dobili njihovi otkrivači ispravni. Na kraju će se problem svesti na pitanje pretvaranja kružnog gibanja u linearno i obrnuto.

2. Parni stroj

1780-ih James Watt usavršio je parni stroj, ostalo je povijest. Međutim, kod parnog stroja bilo je mnogih problema s kojima se njegov izumitelj domišljato borio. Prvi parni stroj bio je oblika prikazanog na slici 1.

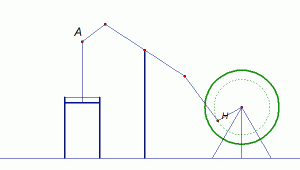1. stroj
Slika 1: Wattov prvi stroj

Točka A giba se po pravcu gore-dolje, a točka B giba se po kružnici i time pokreće kolo. Ovo rješenje nije bilo dovoljno uspješno, stroj se brzo raspadao, a dodatci koje je Watt htio dodati kako bi stroj jače radio nisu se više mogli staviti na ovakvu konstrukciju.

3. Wattov jednostavni linearizirajući mehanizam

Stoga je Watt počeo razmišljati mora li točka A nužno ići po pravcu. Watt se tada dosjetio sljedeće ideje (vidi sliku 2.). Neka su točke O1 i O2 nepomične. Neka se točke B i C miču oko O1 i O2 na jednakim udaljenostima od njih i neka je |BC| isto nepromjenjive vrijednosti. Watt je tada pretpostavio da će točka M, koja je polovište dužine BC, ležati na pravcu.

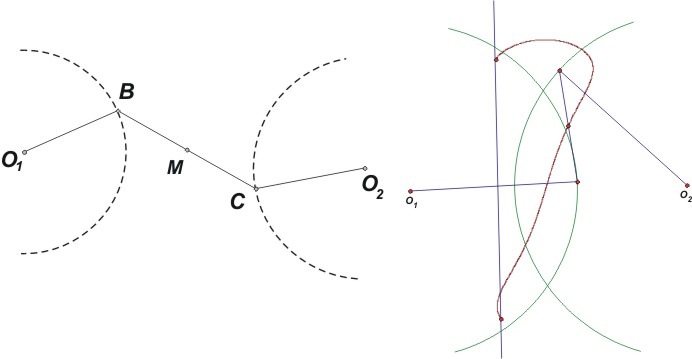Kretanje točke M
Slika 2: Leži li točka M na pravcu?

Sad se postavlja pitanje: koje je geometrijsko mjesto točaka M? Kao iskusni inženjer geometrijski je konstruirao (skicirao) svoju ideju. Watt je otkrio da dobivena krivulja nije pravac, no također je bio svjestan da trajektorija točke M ne odstupa daleko od pravca. Kako bismo lakše vizualizirali gdje točka M zaista leži, pozvat ćemo u pomoć program GSP. On nam omogućuje da pomoću naredbi trace point i locus odredimo geometrijsko mjesto točaka M.

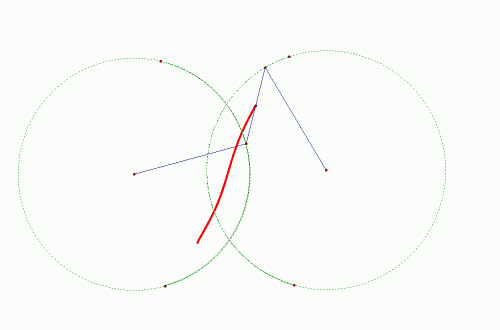Kretanje točke M
Slika 3: Kretanje točke M

Kao rezultat dobivamo sliku 3. Krivulja na slici 3 je krivulja šestog stupnja! No Watt je bio svjestan da krivulja djelomično odstupa od pravca. Na nekim dijelovima čak i previše za praktične potrebe. Postavilo se pitanje mora li M biti polovište ili može biti neka druga točka dužine. Ponovo ćemo koristiti GSP kako bismo to odgonetnuli.

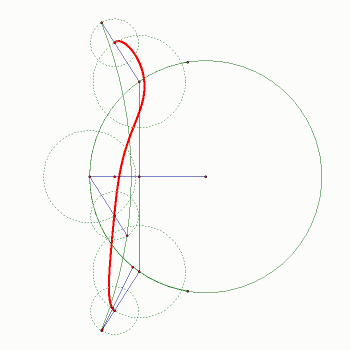Trajektorija
Slika 4: Trajektorija i Wattova konstrukcija

Što bi bilo kad bi točka M dijelila dužinu BC u omjeru 2:1, 1:2, 3:4,... ? Općenito, kako se dobivena krivulja (locus) mijenja kad mijenjamo točku M? Watt (kao iskusni inženjer) je vlastitim približnim konstrukcijama (njemu dostupnim alatom) uspio pokazati da će neki dijelovi krivulje jako malo odstupati od pravca koji je on zamislio. Promjenom omjera krivulja se mogla bolje ,,priljubiti'' uz pravac (vidi sliku 4.). Watt na taj način nije dobio pravac, ali je smanjio odstupanje trajektorije od pravca.

4. Wattov drugi parni stroj

Taj njegov pronalazak omogućio mu je da svoj stroj spoji čvršće i da mu se ne raspada. Tako je nastao Wattov drugi stroj koji je bio dovoljno stabilan za praktične potrebe. Sam Watt smatrao je ovo otkriće (približne krivulje) svojim najvećim znanstvenim postignućem. Pogledajmo sada kako je njegov stroj radio.

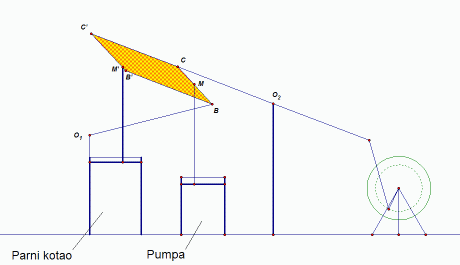2. stroj
Slika 5: Wattov drugi parni stroj

Točke O1 i O2 fiksne su i spojene karikama za točke B i C. Na dužini BC nalazi se točka M koja se kreće po dijelu prethodno opisane krivulje koji najmanje odstupa od pravca. Kako stroj ima dva dijela koja ga pokreću, pumpu za vodu i parni kotao, ta dva dijela moraju se istovremeno kretati tako da se stroj ne raspadne. Taj problem riješen je tzv. Wattovim paralelogramom BCB'C', a točka M odabrana je tako da točke M i M', koje pokreću mehanizam, i točka O2 leže na istom pravcu. Iz sličnosti trokuta C'M'O2 i CMO2 slijedi da je omjer |M'O2| : |MO2| = |C'O2| : |CO2| stalan. Trajektorije točaka M i M' međusobno su homotetične sa središtem O2 i koeficijentom |C'O2| / |CO2|. Ovime je konačno parni stroj bio spreman za upotrebu.

5. Još jedan pokušaj

Pokušaj da se riješi pitanje pretvaranja linearnog u kružno gibanje još će dugo mučiti znanstvenike. Ruski matematičar (i mehaničar) Čebišev istražujući funkcije koje imaju minimalnu devijaciju od nule ponudit će svoj mehanizam. Ovaj mehanizam će isto tako biti približno rješenje problema. Ovdje ćemo demonstrirati kako izgleda mehanizam - više o njemu možete vidjeti u članku [3].

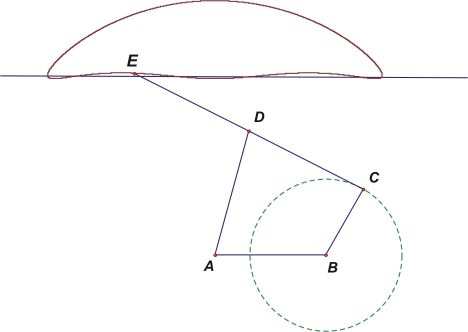Čebiševljev linearizirajući mehanizam
Slika 6: Model Čebiševljevog linearizirajućeg mehanizma

Mehanizam je oblika kao na slici 6. Između njegovih karika vrijede sljedeće relacije:

|ED| = |DC| = |AD| = a, |BC| = b,
3|AB| = |DC| + |AD| + |BC|.

Kao rezultat kretanja točke C po kružnici polumjera b sa središtem u B dobivamo trajektoriju koja je prikazana na slici. Donji dio te trajektorije ima jako mala odstupanja od pravca koji je paralelan s AB. Za vrijednosti a = 1.2 m i b = 0.4 m najveće odstupanje od pravca iznosilo bi 0.0004 m. Stvarno malo! Prednost GSP-a je to što se cijeli mehanizam može konstruirati i oživjeti, a mjere se mogu i provjeriti. (Za više vidi [3].)

6. Rješenje problema

Nakon mnogih pokušaja, problem pretvaranja kružnog gibanja u linearno riješen je tek 1867. Skoro stoljeće kasnije! S obzirom da je riječ o problemu koji pravac mora preslikati u kružnicu i obrnuto, rješenje uključuje inverziju. Dok su nam prethodna rješenja nudila tek aproksiomacije pretvaranja linearnog u kružno gibanje (i obrnuto) ovo je prvo strogo (matematički gledano) rješenje tog problema. Rješenje je ponudio francuski inženjer Charles-Nicolas Peaucellier (1832.-1912.). Do istog otkrića došao je ruski matematičar Lippman Lipkin (živio u Rusiji i Latviji), nazavisno i nešto kasnije od Peaucelliera.

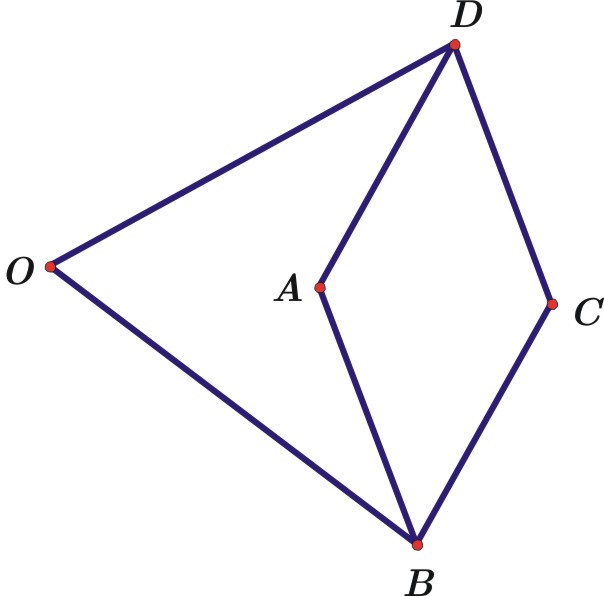Inverzor
Slika 7: Peaucellierov inverzor

Mehanizam na slici 7. ima sljedeće osobine: četverokut ABCD je romb, a karike OD i OB jednakih su duljina i vrijedi |OD| = |OB|. Kad se točka A kreće po pravcu, točka B kreće se po kružnici sa središtem u O. Kad se točka A kreće po kružnici sa središtem u O, točka B kreće se po pravcu. Dakle, naš mehanizam provodi inverziju. Ovo se lako pokaže u GSP-u. (Vidi sliku 8.)

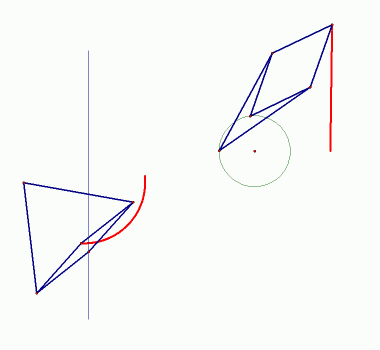Inverzor na dijelu
Slika 8: Pojava inverzije

7. Zaključak

Kako vidimo, program The Geometer's Sketchpad može biti jako koristan u izradi modela gibanja i raznih mehanizama. Ono za što je otkrivačima (,,pionirima znanosti'') trebalo mnogo mukotrpnog posla i papira, mi uz malu pomoć nove tehnologije možemo brzo i lako napraviti i provjeriti njihove rezultate, a oni su se morali bojati da negdje nisu pogriješili u računu.

8. GSP file

Ovaj članak je dorađena verzija članka [4]. Ovdje je objavljen kako bi čitatelji mogli vidjeti animirane verzije slika i uzeti GSP file u kojima su one rađene.

Ovdje možete preuzeti GSP file u kojem su izrađene slike.

9. Literatura

[1]   Malkevitch J., Linkages: From Fingers to Robot Arms, What's New in Mathematics Feature Column Archive, AMS, 2002.

[2]   Solovyov Y., Making the crooked straight, Quantum the student magazine of math and science, vol 1. nr. 2, NSTA, Washington, 1990.

[3]   Tadić T., Model Čebiševljevog linearizirajućeg mehanizma, PlayMath časopis V. gimnazije za matematiku i informatiku, broj 4, Zagreb, 2004.

[4]   Tadić T., Matematika parnog stroja, Poučak časopis za metodiku i nastavu matematike, broj 18-19, HMD i Profil International, Zagreb, 2004.

[5]   Home Page for Virtual Mechanisms, Brock Institute for Advanced Studies, Roxbury

1. Uvod
2. Parni stroj
3. Wattov jednostavni linearizirajući mehanizam
4. Wattov drugi parni stroj
5. Još jedan pokušaj
6. Rješenje problema
7. Zaključak
8. GSP file
9. Literatura