
| Distribucija prim brojeva i Riemannova zeta-funkcija; prvi dio |  |  |
|
Sadržaj: UvodKad su jednom prigodom, prije stotinjak godina, pitali Davida Hilberta bi li mogao reći koji bi to bio glavni problem (tadašnje) matematike, on je odgovorio: "Riemannova hipoteza (RH); to je najveći problem svjetske znanosti uopće, a ne samo matematike!" Naravno, i onda, kao i danas, mnogi bi nematematičari imali (s punim pravom) štošta prigovoriti takvom odgovoru. Ali isto tako, i onda, kao i danas, najveći će dio matematičara reći da RH doista jest centralni matematički problem. Naša je namjera ovdje dati, ili barem pokušati dati, odgovore na sljedeća dva pitanja. Prvo: što je Riemannova hipoteza? I drugo: Zašto je sama RH, i "sve oko nje", toliko važno za matematiku? Kažimo odmah da je odgovor na prvo pitanje zapravo mnogo lakši nego onaj drugi; iako, kako ćemo barem malo vidjeti, poprilično je truda potrebno da bi se krenulo "od nule", i onda u jednom trenu moglo reći da doista razumijemo sam problem i (donekle) zašto to stvarno ima karizmu "tvrda oraha". Naime, drugi odgovor, uz neke neupitne razloge koji govore da bi ispravnost RH imala brojne bitne posljedice u okviru teorije brojeva, zapravo mora imati i jednu "filozofsko- špekulativnu dimenziju". Temeljni razlog ovom posljednjem vezan je uz termin "važnost" koji je, lako ćemo se svi složiti, "apsolutno relativan". Jer čak i u okviru same matematike, moguće je da npr. neka fundamentalna, duboka i/ili originalna spoznaja, ili pak rješenje nekog teškog i važnog problema, u okviru neke matematičke discipline, "ostavi ravnodušnim" matematičare koji se time ne bave. (Naprimjer, nedavni dokaz glasovite slutnje Shimura-Taniyama teško da će pobuditi veću pozornost i uzbuđenje kod nekoga tko se bavi primijenjenom matematikom.) Zato bi jedan dio odgovora mogao biti i ovakav: Tijekom 150 godina, u pokušajima velikog broja slavnih, i manje slavnih matematičara da dokažu RH, napravljen je velik napredak i razvijene su mnoge nove teorije i metode, s mnoštvom velikih teorema, u okvirima mnogih matematičkih disciplina; kako teoriji brojeva, tako i u kompleksnoj analizi, algebarskoj geometriji, teoriji reprezentacija itd. (Ako ništa drugo, uz nezaobilazne muke, patnje, frustracije i neprospavane noći, u rečenih je 150 godina plejada matematičara imala i vrhunsku zabavu; koja još traje...) Sada ćemo dati "prvu grubu aproksimaciju" odgovora na gore spomenuto prvo pitanje. (Nije nam ovdje namjera navesti nešto u nadi da će većina onih koji ovo čitaju odmah i točno razumijeti o čemu je riječ. Namjera je tek "detektirati" neke nepoznate pojmove te eventualno prvi put čuti neke tvrdnje i/ili činjenice, kako bismo dobili ideju za plan o tome "kako dalje". Poseban je naglasak, ili bolje rečeno zamolba, čitatelju da se nikako ne obeshrabri od mogućeg početnog "bombardiranja" mnogim "nepoznanicama"!) Ako je s ∈ C, takav da je njegov realni dio Re s > 1, onda definiramo funkciju ζ(s) kao red
Budući da gornji red konvergira, na Re s > 1, onda je sa s
onda je ta funkcija analitička na Re s > 0. Sa
definirano je (jedinstveno!) meromorfno produljenje od ζ(s) sa skupa Re s > 1 na skup Re s > 0; u s = 1 imamo pol, s reziduumom Ress = 1 ζ(s) = 1. Spomenimo ovdje, zbog važnosti za teoriju, i tzv. integralni oblik meromorfnog produljenja funkcije ζ(s) s Re s > 1 na Re s > 0:
ovdje je, za x ∈ R, { x } := x -
gdje je tzv. kompletirana zeta-funkcija; ovdje je Γ dobro poznata gama-funkcija. Iz ( FJ) lako se dobije i sljedeći identitet, koji se također zove funkcionalna jednadžba:
Primijetimo ovdje fundamentalnu ulogu funkcionalne jednadžbe za teoriju. Naime, ona govori da ako znamo vrijednost zeta-funkcije ζ(s) u proizvoljnom kompleksnom broju s ≠ 0,1, onda znamo i vrijednost zeta-funkcije u broju 1 - s, koji je centralno-simetričan broju s u odnosu na broj 1/2 ∈ C. Ili drugim riječima, dovoljno je razumijeti zeta-funkciju ζ(s) npr. na skupu Re s ≥ 1/2. Dakle, sada imamo ζ(s), funkciju koja je analitička na C \ { 1 }, s polom 1. reda u s = 1. Onda možemo postaviti prirodno pitanje koje se na prvi pogled čini ne sasvim preciznim, a možda i malo naivnim, no pokazuje se da je ono zapravo nevjerojatno duboko i smisleno:
Prvi korak prema željenom odgovoru na to pitanje je jednostavna
posljedica jedne druge fundamentalne opservacije, koju dugujemo
L. Euleru,
o vezi zeta-funkcije i skupa prim brojeva
Spomenuta jednostavna posljedica od ( EPF) glasi: Drugi je korak dokaz sljedećeg netrivijalnog i važnog rezultata koji je, među ostalim, bio i ključni moment u slavnom dokazu tzv. Teorema o prim brojevima, koji su na kraju 19. stoljeća dali, neovisno jedan o drugome, J. Hadamard i C.-J. de la Vallée Poussin; više o tome kasnije.
Dalje, kao jednostavna posljedica ( FJ), pokaže se ova činjenica: to su tzv. trivijalne nultočke zeta-funkcije. Isto tako, lako se vidi da je posebno ζ(0) = -1/2, a onda kao posljedicu gornjeg teorema, i ponovo funkcionalne jednadžbe, imamo ovu činjenicu: Kao rezime svega do sada rečenog, slijedi da se u vezi s gore postavljenim pitanjem o nultočkama zeta-funkcije moramo koncentrirati na (otvorenu) "prugu"
u kompleksnoj ravnini C. Naime, sve (eventualne)
ne-trivijalne nultočke zeta-funkcije ζ(s) nalaze se unutar
te pruge, koja se zove kritična pruga. Teorija Riemannove
zeta-funkcije (i mnogih njezinih generalizacija, kao što su razne
vrste tzv. L-funkcija), u posljednjih stotinjak godina, bavi
se poglavito problemom lociranja skupa nultočaka
Kažimo ovdje tek dvije stvari o ( RH). Prvo: unatoč detaljnom
proučavanju svih pronađenih Riemannovih
rukopisa/neobjavljenih radova, koji se nalaze u Niedersächische
Staats und Universitäts Bibliothek u Götttingenu, do dana
današnjeg nisu jasni svi razlozi koji su ga ponukali na
formulaciju te glasovite slutnje. I drugo: iako je velik broj
eksperata danas sklon vjerovati da (RH) jest točna,
mnogi će ipak reći da postoji "realna mogućnost" i za
onaj drugi (jako neželjeni!) ishod. Bilo kako bilo, u Odjeljku 7
vidjet ćemo da su mnogi važni i duboki rezultati, u smjeru
(eventualnog) dokaza ( RH), dobiveni. (A to će onda dati i
neke vrlo "uvjerljive" razloge za spomenuto vjerovanje da (
RH) doista stoji.) Ali isto tako, moglo bi se reći kako je
zapravo nevjerojatno da se usprkos enormnim naporima brojnih
matematičara, u izvjesnom smislu, još uvijek malo zna o skupu
nultočaka
Ovaj je pregledni rad prvi dio nečega što bi se moglo zvati "Uvod u Analitičku teoriju brojeva; Riemannova zeta-funkcija i Riemannova hipoteza"; za više detalja vidjeti npr. [Ed], [Pa] i [Ch], ili [Iv] i [Ti] ako se želi doći još dalje. Kao što smo već rekli, namjera je pokušati objasniti što je teorija Riemannove zeta-funkcije, što je RH i kakve to sve ima veze s nekim drugim problemima matematike i/ili teorijama. Ali, kao što se već moglo vidjeti iz gore navedenoga, nije baš sasvim jednostavno govoriti o tim stvarima nemamo li neko minimalno predznanje o analitičkim funkcijama i elementarnoj teoriji brojeva. Imajući to na umu, u nadi da se "netrenirani" čitatelj neće brzo "umoriti", napravili smo jedan kompromis u našem izlaganju. Naime, neminovno je kada je riječ o ovakvim situacijama ("razuman" opseg/duljina rada), da većinom moramo "preskakati" znatne dijelove teorija (uglavnom analitičke teorije brojeva i teorije analitičkih funkcija) da bismo dobili povezanu i smislenu, a u isto vrijeme dosta kratku "priču". No, takav pristup nosi "realnu opasnost" da onoga tko to čita ti "skokovi" za koje nismo dali odgovarajuće argumente stavljaju u "nelagodan osjećaj". Zato se naš kompromis sastoji u sljedećem. U ovom prvom dijelu, nakon što smo zapravo već rekli što je RH, s podosta detalja u dva odjeljka govorimo o nekim stvarima koje su priprema za ono što će slijediti. Tako u Odjeljku 1, koji nosi naslov "Kompleksna analiza", dajemo kratak pregled nekih osnovnih pojmova i rezultata o analitičkim funkcijama, koji su u isto vrijeme nezaobilazno oruđe analitičke teorije brojeva. Taj je odjeljak zamišljen kao skup "naputaka i komentara" koji će čitatelju pomoći kada (eventualno) samostalno krene na "put" od definicije derivacije kompleksne funkcije pa do fundamentalnog Hadamardova teorema faktorizacije. Odjeljak 2 ima za namjeru staviti analitičku teoriju brojeva u "povijesni kontekst". Naime, ta je teorija fundirana u 19. stoljeću, u radovima niza matematičara: npr. Gaussa, Dirichleta, Riemanna, Hadamarda, von Mangoldta, Mertensa i dr. Kao početak uzima se rad na dva velika problema tadašnje matematike, koji je rezultirao dvama osnovnim teoremima: Teoremom o prim brojevima i Dirichletovim teoremom o prim brojevima u aritmetičkim nizovima. U Odjeljku 2 precizno formuliramo te teoreme i dajemo neke potrebne napomene i argumente. Napokon, kao treći dio toga odjeljka, s dosta detalja dajemo tek mali dio cijele teorije zeta-funkcije; preciznije, računamo ζ(2k), za k ∈ N. Tu nam je namjera bila pokušati na primjeru dati "osjećaj" da se vidi koja to vrsta argumenata i/ili rezultata figurira u teoriji. Namjera je, u planiranom drugom dijelu ovog rada, govoriti o sljedećim temama:
U Odjeljcima 3 i 4 navest ćemo, uglavnom bez puno argumenata, glavne korake u dokazima navedenih teorema, te objasniti neke važne pojmove kao što je npr. pojam L-funkcije. Odjeljci 5 i 6 navest će, ukratko, činjenice o gama-funkciji i o funkcionalnoj jednadžbi. U Odjeljku 7 reći ćemo koji su to glavni do danas poznati rezultati o nultočkama zeta-funkcije, te zašto je RH važan matematički problem. Naglasimo ovdje da ovaj rad nema nikakvu namjeru niti spomenuti makar i najmanji dio onoga što je, na ovaj ili onaj način, u cijelosti ili dijelom, proizišlo iz klasične teorije zeta-funkcije i Dirichletovih L-funkcija (npr. modularne i automorfne forme, razne druge vrste L-funkcija, eliptičke krivulje itd.). Zainteresirani će čitatelj zasigurno lako doći do eventualno potrebne literature. Na kraju ovog Uvoda ugodna mi je dužnost zahvaliti svojim prijateljima i kolegama A. Dujelli, I. Gusiću i M. Vukoviću na nekim korisnim savjetima i napomenama u vezi s ovim radom. Napomena. Pri spominjanju prezimena nekih slavnih matematičara, s pomoću "hiperlinka" (veze), sugerira se čitatelju da dozna više detalja, npr. na [Hi]. Isto tako, naglasimo da se o nekim neobjašnjenim pojmovima i/ili rezultatima u tekstu više može pronaći npr. na [Wi]. 1. Kompleksna analizaTeorija Riemannove zeta-funkcije i raznih drugih sličnih objekata (npr. L-funkcija) pripada grani teorije brojeva koja se zove analitička teorija brojeva. Ovdje pridjev "analitička" stoji zato jer tu kao dva glavna izvora korištenih metoda i rezultata jesu kompleksna analiza i (komutativna) harmonijska analiza; vidi Odjeljak 6. Glavni je cilj ovog uvodnog odjeljka dati koncizan pregled kroz materiju kompleksne analize, potrebne za ono što slijedi. Napomenimo da se dobar dio onoga što nama ovdje treba predaje u okviru kolegija "Kompleksna analiza" i "Teorija analitičkih funkcija" za studente PMF-MO-a. (Za više detalja i značenje nekih pojmova koji nisu dolje precizno objašnjeni, vidite npr. [KK], [Un]; za temeljitije proučavanje kompleksne analize vidite npr. [Ma].) Za funkciju f : Ω → C, gdje je skup Ω ⊆ C otvoren, kažemo da je derivabilna u točki z0∈ Ω ako postoji limes
broj f &prime(z0) zovemo derivacijom od f u z0. Kažemo da je f derivabilna na Ω, ako je ona derivabilna u svakoj točki z0 iz Ω. Kao fenomenalna i gotovo nevjerojatna pokazuje se činjenica da svaku derivabilnu funkciju f : Ω → C možemo u "maloj" okolini bilo koje točke z0 ∈ Ω razviti u Taylorov red
Podsjetimo da se funkcije koje imaju Taylorov razvoj još zovu i analitičke funkcije, pa tako imamo da su pojmovi "derivabilna funkcija" i "analitička funkcija", u kompleksnoj analizi, sinonimi. Iz tog se razloga kompleksna analiza često zove i teorija analitičkih funkcija. Dalje se pokazuje i ovaj jednostavan, ali za nas ovdje vrlo bitan rezultat.
Ako je Ω ⊆ C neki podskup i f : Ω → C funkcija, kažemo da je točka z0 ∈ Int Ω ( := nutrina zatvarača od Ω) singularitet od f, ako f u z0 nije derivabilna ili uopće nije definirana; nas zanimaju samo funkcije s izoliranim singularitetima. Dobro je poznata podjela singulariteta na uklonjive singularitete, polove i bitne singularitete; nas uglavnom zanimaju funkcije čiji su svi singulariteti polovi. Podsjetimo se da je funkcija f cijela ako je definirana na čitavom C, te je na čitavom C i derivabilna; npr., kompleksni polinomi i funkcije ez, sin z, cos z su cijele. Nadalje, funkcija f je meromorfna na C, ako postoje cijele funkcije g, h takve da je f = g / h i h nije ekvivalentna 0. (Primijetimo da su zapravo meromorfne funkcije poopćenje racionalnih funkcija; inače, u grčkom μερoσ znači "razlomak", a μoρφη znači "oblik".) Iz niže navedenog Weierstrassovog teorema slijedi sljedeći rezultat (v. [Ma], Vol. II, Sect. 50).
Dalje; dobro je poznato da se, npr. Cauchyjevom metodom, meromorfne funkcije mogu razvijati u parcijalne razlomke. Tako imamo npr. rastav funkcije ctg z na parcijalne razlomke
tu imamo lokalno uniformnu konvergenciju gornjeg reda na
C \ Za teoriju analitičkih funkcija fundamentalan je i pojam beskonačnog produkta, tj., metoda razvoja analitičke funkcije u beskonačan produkt; razlog za to je taj da će tako napisana funkcija imati bolju vezu sa skupom svojih nultočaka. Naime, za niz (an) u C*=C \ { 0} definiramo tzv. niz parcijalnih produkata pn := a1 ··· an. Ako postoji p ∈ C* takav da niz (pn) konvergira prema p, onda kažemo da beskonačan produkt Π n an konvergira, prema p. Primijetimo: ako Π n an konvergira, onda je lim n an = lim n pn / p n-1 = 1. Zato je uobičajeno pisati an = 1 + un; jasno, lim n un = 0. Jedna od osnovnih činjenica o beskonačnim produktima je ta da se oni mogu logaritmirati; tj. imamo ovu propoziciju koja povezuje beskonačne produkte s redovima.
Posebno su zanimljivi beskonačni produkti funkcija; tj. kada umjesto niza brojeva (un) gledamo niz funkcija un : Ω → C, za neki podskup Ω ⊆ C. Za takve je produkte jedan od glavnih rezultata ovaj teorem.
Kažimo ovdje još i to da je korisno klasu beskonačnih produkata malo proširiti tako da dopustimo da u Π nan bude najviše konačno mnogo an-ova jednakih 0; tj., ∃ N ∈ N takav da an ≠ 0, ∀ n>N. Onda kažemo da Πn an konvergira ako produkt Πn > N an konvergira u smislu prije dane definicije konvergencije. Razlog za tu proširenu definiciju je ovaj: sada, za neki Πn an imamo da je taj beskonačan produkt jednak 0 ako i samo ako postoji n takav da je an = 0, što možemo shvatiti kao generalizaciju činjenice, naučene u osnovnoj školi, da je C integralna domena. Do kraja ovog odjeljka cilj nam je navesti još dva osnovna teorema o analitičkim funkcijama; jedan je Weierstrassov, a drugi Hadamardov. Posebno, Hadamardov teorem osnova je za ozbiljnije proučavanje nultočaka cijelih funkcija, a onda i meromorfnih funkcija; mi ćemo to primijeniti na zeta-funkciju. Ali, kao motivaciju za ono što slijedi, pogledat ćemo jedan specijalan slučaj. Najprije, ako je dan neki polinom P(z)∈ C[z], stupnja deg (P) ≥ 1, onda se on može napisati kao za neki a ∈ N0 i polinom P1(z) takav da P1(0) ≠ 0. Ako je i stupanj deg (P1) = k ≥ 1, onda postoji c ∈ C i (ne nužno međusobno različiti) z1,... , zk ∈ C* takvi da je to je zapravo Osnovni teorem algebre. Imajući u vidu da je P1(0) = c (-z1)··· (-zk), slijedi
Neka je sada
Primijetimo da je f1(0)=1 i
Naravno, nije baš jasno jesmo li mi tu uopće dobili smislen identitet. No, iako je naš "argument" bio "sirova analogija" s Osnovnim teoremom algebre, pokazuje se da napisani identitet za sin z doista vrijedi; istini za volju, treba poprilično "teorije" (npr. Hadamardov teorem faktorizacije) da bismo to rigorozno opravdali...
Pretpostavimo sada da je f(z) cijela transcendentna
funkcija, ili kraće CTF; to je funkcija koja je cijela i nije
polinom. Isto tako, pretpostavimo da je skup nultočaka
pojam "standardno numeriran" znači da svaka nultočka ≠
0 od f dolazi u gornjem nizu onoliko puta kolika joj je kratnost.
(Primijetimo, kao jednostavnu posljedicu činjenice da su nultočke
analitičke funkcije izolirane, da je limn an = ∞.)
Cilj nam je funkciju f(z) "raspisati po nultočkama u pogodnoj
formi beskonačnog produkta"; to će biti Hadamardov teorem
faktorizacije, koji se može shvatiti kao poopćenje Osnovnog
teorema algebre (za slučaj polja C). Ali najprije imamo
važan pripremni rezultat. Njegov prvi dio govori da za
svaki standardno numeriran niz kompleksnih brojeva, koji
još pritom teži u beskonačnost, postoji bar jedna CTF f
kojoj je taj niz upravo skup nultočaka
Ako pozorno pogledamo gornju faktorizaciju od f, vidimo da je za
n ∈ N odgovarajući faktor, u beskonačnom produktu,
oblika "(1 - z/an)−puta−exp (polinom stupnja n)".
Pitanje, ne sasvim precizno, je može li se ovdje faktor exp(···) nekako
pojednostavniti. Odgovor je "DA"; i to bitno.
No prije nego što damo preciznu tvrdnju, moramo uvesti još neke
oznake i pojmove, kao što su npr. "red funkcije" i "eksponent
konvergencije niza". Prvo: ako je f cijela funkcija, za r > 0
definiramo M(r) := max |z| = r | f(z)| ;
r
Sada definirajmo pojam eksponenta konvergencije.
Vezano uz eksponent konvergencije, definirajmo još jednu veličinu. Ako je (an) niz kao gore, neka je κ najveći među svim k ∈ N0 takvima da red ∑ n1/ | an | k divergira. Sada napokon možemo iskazati ovaj osnovni teorem (v. [Ma], Vol. II, Sect. 48).
Napomena. Nije teško vidjeti da se eksponent konvergencije τ, nekog niza (an), računa kao
Nadalje, iz definicije broja κ jasno je da imamo nejednakosti κ ≤ [τ ] i τ ≤ κ + 1. Zatim, još jedan netrivijalan Hadamardov rezultat je nejednakost τ ≤ ρ. Posljedica gornjih dviju tvrdnji je i nejedankost κ ≤ [ρ]. 2. Povijest i motivacija; od Eulera do RiemannaPovijesno gledajući, postoje dva "važna puta" koja su rezultirala dvama osnovnim teoremima onoga što danas zovemo analitičkom teorijom brojeva; isti su bili među glavnim dostignućima matematike 19. stoljeća, a osim toga rezultirali su i razvojem ideja i teorija, te formulacijom novih zanimljivih problema, koji su i dan-danas u centru modernih matematičkih istraživanja. Ta dva teorema su tzv. Teorem o prim brojevima i Dirichletov teorem (o prim brojevima u aritmetičkim nizovima). Ono što je posebno interesantno, kako ćemo vidjeti, je činjenica da se kao "glavna glumica" u cijeloj toj teoriji pojavljuje upravo zeta-funkcija. Cilj ovog odjeljka je formulirati rečene teoreme i objasniti povijesni kontekst u kojem su nastali, te navesti još neke relevantne rezultate i dati/skicirati dokaze za neke od njih. Prvo ćemo se kratko pozabaviti Teoremom o prim brojevima, a onda Dirichletovim teoremom čiji je dokaz, usput rečeno, bio pravi izvor ideja i metoda za matematiku 20. stoljeća.
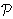 = {2, 3, 5, 7, 11, 13, 17, 19…} = {2, 3, 5, 7, 11, 13, 17, 19…}
Sljedeće dvije činjenice o prim brojevima bile su dobro poznate već i u antičkoj Grčkoj (Euklid, Elementi, knjiga 9):
Sada bismo mogli reći da su prim brojevi "osnovni
blokovi" od kojih se, s pomoću operacije množenja, dobivaju svi
ostali prirodni brojevi; i tih "blokova" ima beskonačno mnogo.
Ali jedna od najvećih zagonetki koja muči matematičare već
nekoliko tisućljeća je tzv. problem distribucije prim
brojeva; ili, kako je 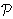 u N? u N?
No da bismo o tome mogli nešto zanimljivo reći, moramo napraviti malu pripremu. Prvo: za proizvoljan x ∈ [2,∞ ) definirajmo 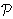 | p ≤ x}. | p ≤ x}.
Tako dobivamo funkciju π : [2,∞ ) → N, koja računa broj prim brojeva p koji su manji ili jednaki od nekog zadanog realnog broja x; npr., π(5) = 3, π(10) = 4, π(30) = 10, π(100) = 25… Jedan od prvih velikih problema matematike 19. stoljeća bio je razumjeti ponašanje te funkcije; ili, malo preciznije, dobiti informaciju o asimptotskom ponašanju od π. Prvu "pravu" heurističku opservaciju, ili bolje rečeno slutnju o tom problemu načinili su C.F. Gauss i A.M. Legendre, negdje na prijelazu iz 18. u 19. stoljeće. U pokušajima niza velikih matematičara toga vremena da se rečena slutnja dokaže, ključnim se korakom pokazao rad B. Riemanna Über die Anzahl der Primzahlen unter einer gegebenen Grösse, objavljen 1859. godine (v. [Ed] za eng. prijevod tog monumentalnog djela). U tom kratkom radu, jedinom iz Teorije brojeva koji je objavio, Riemann je vrlo precizno dao skicu željenog dokaza. U njegovu se pristupu apsolutno bitnom pokazala ideja da se centralnim objektom u okviru rečenog problema promatra zeta-funkcija. I to ne, kako su to radili matematičari prije njega, da se ona gleda kao realna funkcija realne varijable, nego kao kompleksna funkcija kompleksne varijable. Napomenimo ipak da je, usprkos fundamentalnim idejama, za rigoroznu realizaciju istih trebalo nekoliko desetljeća. Naime, tek na kraju 19. stoljeća napokon je dobiven detaljan dokaz, u radovima dvojice matematičara, Hadamarda i de la Valée Poussina, koji su neovisno radili na tome. Kažimo i to da je taj dokaz u biti "čekao" da se teorija analitičkih funkcija razvije u toj mjeri da uspješno može "servisirati" tom "fragmentu" analitičke teorije brojeva. (U tom se poslu, kao centralna figura, našao upravo Hadamard, čiji je navedeni Teorem faktorizacije zapravo kruna mnogogodišnjih napora.) Sljedeći je teorem precizna forma rečene slutnje; više o njegovu dokazu reći ćemo u Odjeljku 4.
Gornji je identitet poslužio Euleru za dokaz, potpuno različit
od Euklidova (v. Napomenu koja slijedi), da ima beskonačno mnogo
prim brojeva. Naime, kad bi skup prim brojeva
Primijetimo kako odavde opet slijedi da je skup
Napomena. (2) Dokaz tvrdnje da postoji beskonačno mnogo prim brojeva oblika 4n+1 malo je teži; za dokaz koji se koristi tzv. Malim Fermatovim teoremom vidite npr. [Du], str. 21. Gornji Eulerovi rezultati i dani argumenti koji ih dokazuju, bili su direktna motivacija P.G.L. Dirichletu za formulaciju i dokaz njegova slavnog Teorema o prim brojevima u aritmetičkim nizovima.
To je Eulera motiviralo i zainteresiralo za općenito računanje redova oblika ζ(x), posebno kada je x ∈ N. Kao rezultat njegova rada na tom problemu dobiven je niže navedeni teorem, koji računa vrijednosti zeta-funkcije u parnim prirodnim brojevima. Tako je, specijalno,
No, prije nego što iskažemo sam taj teorem i damo skicu njegova dokaza, moramo napraviti malu pripremu o tzv. Bernoullijevim brojevima. Jacob Bernoulli u djelu Ars Conjectandi (1713) proučava problem nalaženja opće formule za zbroj k-tih potencija prvih nekoliko prirodnih brojeva, tj. Računa se
gdje je
Sada, ako F shvatimo kao kompleksnu funkciju, ona je očito derivabilna u svim točkama u kojime je i definirana. Drugim riječima, F je derivabilna u svim točkama iz C, osim u z takvima da je ez - 1 = 0, tj. F je derivabilna u svakom F takvom da je z ≠ ± 2lπ i, l∈N. Posebno je F analitička na skupu |z| < 2π, pa tamo ima Taylorov razvoj, oko z0 = 0,
za neke koeficijente Bn ∈C.
Napomena.
Nadalje, lako se pokazuje da Bernoullijeve brojeve možemo rekurzivno računati iz identiteta
Posebno je onda npr.
Nadalje, iz
usporedbom koeficijenata uz z2k+1 slijedi da je Kao rezime gornjih razmatranja imamo Taylorov razvoj funkcije F:
Sada, koristeći se dobro poznatom Eulerovom formulom odmah se pokazuje da je
Množenjem te jednakosti sa z i stavljanjem 2i z umjesto z u gornji Taylorov razvoj od F, dobivamo Taylorov razvoj od z ctg z oko 0:
Zamjenom z ↔ zπ slijedi
S druge strane, u Odjeljku 1 dali smo rastav funkcije ctg z na parcijalne razlomke. Ako i tamo stavimo zamjenu z ↔ zπ, dobit ćemo
Ali, za |z| < 1, koristeći se razvojem od (1- z2/ m2)-1 u geometrijski red ∑k ≥ 0 z2k / m2k, zamjenom poretka sumiranja dobivamo
Izjednačavanjem Taylorova razvoja funkcije π ctg π z s njezinim rastavom na parcijalne razlomke, uz korištenje posljednje jednakosti, dobit ćemo
Usporedbom koeficijenata uz z2k-1 slijedi najavljeni teorem.
Napomena.
To govori da će za k "velik" i pripadni Bernoullijev broj B2k biti "velik po apsolutnoj vrijednosti" i posebno lim k → ∞ | B2k| =∞ (usp. s vrijednostima B2 = 1/6, B4 = -1/30 i B6 = 1/42). Nadalje, budući da je očito lim k → ∞ ζ(2k) = 1, slijedi da je
Uzmimo sada funkciju sekans sec z = 1 / cos z te napišimo njezin Taylorov razvoj oko 0 kao sec z = ∑k≥0 ckzk, za neke koeficijente ck ∈ C. (Jer je sec parna funkcija, vidi se da je zapravo c2k-1 = 0, za sve k ∈ N.) Ako definiramo tzv. Eulerove brojeve onda gornji Taylorov razvoj možemo zapisati kao
Slično kao što smo imali za Bernoullijeve brojeve, lako možemo pokazati da Eulerovi brojevi zadovoljavaju rekurziju
odavde slijedi E2k ∈ Z i posebno: Sada možemo navesti još jednu zanimljivu propoziciju, čiji su specijalni slučajevi sljedeći dobro poznati identiteti:
Kažimo da je dokaz ove propozicije analogan dokazu prethodnog teorema. Naime, samo treba izjednačiti Taylorov razvoj za sec z s razvojem te funkcije na parcijalne razlomke
tu imamo lokalno uniformnu konvergenciju gornjeg reda na
C \
Kao završetak, kažimo tek nekoliko riječi o onome čime smo započeli ovo naše razmatranje koje je rezultiralo gornjim teoremom i propozicijom. To je spomenuti Eulerov interes za računanjem ζ(x), za neke posebne vrijednosti od x. Nakon dobivenih vrijednosti u teoremu, za x = 2k kada je k ∈N, sljedi prirodno pitanje: Spomenimo tek ovdje, koliko god to možda čudno zvučalo, da je to otvoreni problem! Preciznije rečeno, ne zna se točna vrijednost ζ(n) ni za koji neparan n ≥ 3. Štoviše, osim nekih zanimljivih informacija o prvih nekoliko neparnih prirodnih brojeva, ne zna se je li uopće konkretan ζ(n) iracionalan broj (v. npr. [Po], [Ri] i [Zu]). No ipak, usprkos rečenom neznanju, postoji slutnja koja govori da je Literatura
Uvod |

 ζ(s) dobro definirana funkcija. Ta se funkcija zove
Riemannova zeta-funkcija. Budući da je konvergencija reda koji
definira ζ(s) apsolutna i lokalno uniformna, na Re s > 1,
lako se pokazuje da je ta funkcija na spomenutom skupu štoviše
i analitička. No onda je razumno pitati postoji li njezino
analitičko/meromorfno produljenje na neki veći podskup
od C. Kao prvi korak, pokazuje se da postoji meromorfno
produljenje od ζ(s) na Re s > 0, s jedinim polom, 1.
reda, u s = 1. Sasvim precizno, ako definiramo funkciju ζ
2(s) redom
ζ(s) dobro definirana funkcija. Ta se funkcija zove
Riemannova zeta-funkcija. Budući da je konvergencija reda koji
definira ζ(s) apsolutna i lokalno uniformna, na Re s > 1,
lako se pokazuje da je ta funkcija na spomenutom skupu štoviše
i analitička. No onda je razumno pitati postoji li njezino
analitičko/meromorfno produljenje na neki veći podskup
od C. Kao prvi korak, pokazuje se da postoji meromorfno
produljenje od ζ(s) na Re s > 0, s jedinim polom, 1.
reda, u s = 1. Sasvim precizno, ako definiramo funkciju ζ
2(s) redom

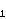
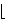 x
x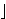 tzv.
razlomljeni dio od x. Sljedeći je korak pokazati da
ζ(s) štoviše ima meromorfno produljenje na cijeli
C, ili drukčije rečeno da ima analitičko
produljenje na C \ {1} te da zadovoljava
funkcionalnu jednadžbu
tzv.
razlomljeni dio od x. Sljedeći je korak pokazati da
ζ(s) štoviše ima meromorfno produljenje na cijeli
C, ili drukčije rečeno da ima analitičko
produljenje na C \ {1} te da zadovoljava
funkcionalnu jednadžbu
 (ζ) od
zeta-funkcije ζ(s)?
(ζ) od
zeta-funkcije ζ(s)?
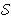 ⊆ C takav da: (1)
⊆ C takav da: (1)
 Pojam prim broja p u skupu prirodnih brojeva
N je fundamentalan. Skup svih prim brojeva u N
označavat ćemo s
Pojam prim broja p u skupu prirodnih brojeva
N je fundamentalan. Skup svih prim brojeva u N
označavat ćemo s