
 |
Hrvatski matematički elektronski časopis math.e | |
| Broj 8 | ||
| http://web.math.hr/mathe/ |
Sadržaj:
0. Uvod
1. Crtanje pomoću Wangovih pločica
2. Računanje pomoću Wangovih pločica
3. Neodlučivost problema popločavanja
4. Jedan aperiodičan skup Wangovih pločica
Literatura
Wangove pločice su kvadrati kojima su rubovi obilježeni bojom. Možemo ih slagati jednu do druge, ali samo ako su im oznake na dodirnim rubovima odgovarajuće - kao u nekad popularnoj igrici Tetravex. U toj su igrici rubovi, umjesto bojama, označeni brojevima:
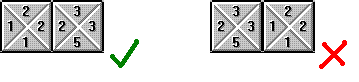
Kao i u toj igrici, dan nam je skup pločica koje smijemo koristiti i pločice ne možemo okretati, već samo pomicati. Za razliku od igrice, ne pokušavamo popločati neki veći kvadrat, nego cijelu ravninu. Svaku pločicu smijemo koristiti onoliko puta koliko želimo - pločica nije "potrošena" kad smo je jednom upotrijebili.
Kineski matematičar Hao Wang je pločice, kasnije nazvane po njemu, prvi put počeo promatrati u kontekstu pitanja odlučivosti popločavanja ravnine. Pitao se postoji li algoritam koji u konačno mnogo koraka za dani skup pločica određuje je li moguće njima popločati ravninu. Pokazalo se da odgovor na to pitanje ovisi o tome postoje li aperiodični skupovi pločica.
Definiciju popločavanja ravnine i više o različitim pravilnim popločavanjima možete pročitati u prethodnom broju Math.e, u članku [KR]. Ovdje ćemo se baviti pitanjem je li neko popločavanje periodično ili nije. Za popločavanje ravnine (bilo kakvim skupom pločica, ne nužno Wangovim pločicama) kažemo da je periodično ako se neki njegov komad stalno ponavlja - točnije, ako postoje dva nekolinearna vektora takva da translacije za te vektore prevode popločavanje u njega samog. Sva popločavanja u članku [KR] bila su periodična.
Ako se radi o popločavanju Wangovim pločicama, dakle kvadratima, periodičnost znači da postoje prirodni brojevi n i m takvi da se vodoravno uzorak ponavlja svakih n pločica, a vertikalno svakih m pločica (dakle, da se stalno ponavlja jedan n×m pravokutnik). Ako ne postoje takve translacije, popločavanje se naziva neperiodičnim.
Postoje skupovi pločica kojima se ravnina može popločati samo periodično. Takav je, na primjer, skup od samo jedne Wangove pločice kojoj su svi rubovi obojeni jednako:

Također, jasno je da postoje skupovi pločica kojima se ravnina može popločati periodično ili neperiodično. Takav je, na primjer, kvadrat: jedno periodično popločavanje vidimo gore, a neperiodično popločavanje dobijemo tako da svaki redak malo pomaknemo, pazeći pritom da se pomaci ne ponavljaju periodično:

Međutim, pitanje postoji li skup pločica kojima se ravnina može popločati, ali samo neperiodično, nije tako lako. Takav skup pločica zovemo aperiodičnim.
Wangu je za odgovor na pitanje o postojanju algoritma koji ispituje može li se zadanim skupom pločica popločati ravnina trebao odgovor na drugo pitanje: "Postoji li aperiodičan skup pločica?". Naime, pronašao je algoritam za Wangove pločice, ali za aperiodične skupove Wangovih pločica algoritam se nikada ne bi zaustavio. Budući da dotada (1961.) nije bio poznat nijedan aperiodičan skup pločica, činilo se prirodnim postaviti Wangovu slutnju:
Ne postoji aperiodičan skup pločica.
Robert Berger je 1966. u svojoj doktorskoj disertaciji opovrgnuo Wangovu slutnju. On je povezao Wangove pločice s Turingovim strojevima. Turingov stroj je model računala koji se sastoji od beskonačne trake, podijeljene na polja, na kojoj su zapisani ulazni podaci i čitača koji se u svakom trenutku nalazi na jednom od polja. Čitač može biti u nekom od konačno mnogo stanja i, ovisno o stanju u kojem je i podatku koji očita s polja nad kojim se nalazi, on briše podatak na polju, upisuje novi, prebacuje se u neko drugo stanje i pomiče se jedno polje ulijevo ili udesno. Neka stanja stroja su završna - kad dobije uputu da se prebaci u to stanje, stroj staje i u tom su trenutku na traci zapisani izlazni podaci.
Berger je pokazao da se svaki Turingov stroj može implementirati pomoću skupa Wangovih pločica: stanje trake na početku, kad su na njoj ulazni podaci, kodira se pomoću Wangovih pločica u jedan red. Nakon toga oznake na rubovima pločica pomoću kojih pokušavamo sastaviti drugi red (oznake na rubovima se moraju poklapati!) diktiraju točno kako drugi red mora izgledati i tako dalje. Svaki sljedeći red tako kodira izgled trake Turingovog stroja nakon sljedećeg koraka. Na kraju, u zadnjem redu tog popločavanja dobivamo izgled trake Turingovog stroja s izlaznim podacima. Ako se baš želi popločati cijela ravnina, može se u skup dodati jedna pločica bez informacija i njome popuniti sva neiskorištena polja. Primjer takve implementacije možete vidjeti na donjoj slici, na kojoj je implementiran jednostavan Turingov stroj koji za ulaz n (pločica s bijelim kvadratom u sredini) računa n+2 (pločica s crnim kvadratom u sredini). Stanja stroja kodirana su plavom, zelenom i ružičastom bojom, a pločice s četirima sivim rubovima ne nose nikakvu informaciju; tu su samo da poploče dio ravnine u kojem se ne odvija računanje.
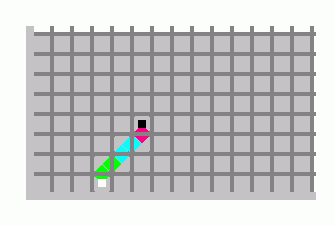
Time je Berger pokazao da se pomoću Wangovih pločica može računati. Nešto više o tome reći ćemo u 2. poglavlju, u kojem ćemo konstruirati nekoliko skupova pločica koji provode osnovne račune, npr. zbrajaju ili množe dva broja. Ta činjenica koristi se i u zapletu Eganove SF priče "Wangovi sagovi" [EG]. Međutim, osim što je zanimljiva sama po sebi, mogućnost implementiranja Turingovih strojeva Wangovim pločicama ima još jednu posljedicu. Pokazuje se da je zbog nje pitanje odlučivosti popločavanja ravnine ("Postoji li algoritam koji za dani skup pločica određuje je li moguće njima popločati ravninu?") ekvivalentno pitanju odlučivosti zaustavljanja Turingovog stroja ("Postoji li algoritam koji određuje hoće li dani Turingov stroj stati nakon konačno mnogo koraka?"). Time je prvo pitanje riješeno jer se 1966., kad je Berger napisao disertaciju, već znalo da je odgovor na drugo pitanje "NE". Naime, iako je moguće prepoznati neke strojeve koji ne staju nakon konačno mnogo koraka, ne postoji algoritam koji za svaki stroj određuje hoće li ikada doći u završno stanje.
Posljedica neodlučivosti problema popločavanja ravnine Wangovim pločicama jest i postojanje aperiodičnog skupa Wangovih pločica. Možemo li ga konstruirati? Originalni Bergerov dokaz samo je posredno, preko veze s Turingovim strojevima, dokazivao postojanje takvog skupa pločica. Međutim, iz tog dokaza i dokaza o neodlučivosti problema zaustavljanja, Berger je uspio pronaći skup od 20462 pločice pomoću kojih se ravnina može popločati, ali samo neperiodično. Taj broj pločica kasnije je on sam smanjio na 104, zatim su uslijedila smanjenja na 92 (Knuth), 52 (Robinson), 40 (Läuchi), 35 (Robinson), 34 (Penrose), 32 (Robinson), 24 (Robinson), 16 (Ammann), 14 (Kari) i 13 (Culik). Osim toga, dokazano je da ne postoji aperiodičan skup s manje od 4 pločice - time je prostor za poboljšanja smanjen na skupove pločica veličine između 4 i 13. Na sljedećoj slici (preuzetoj iz [WI]) prikazan je Culikov 13-člani, danas najmanji poznati aperiodičan skup Wangovih pločica. Detaljnije ćemo ga opisati u 4. poglavlju.
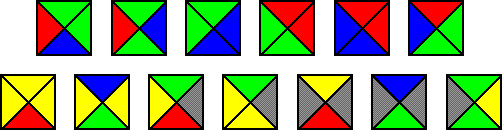
Danas se Wangove pločice i njihovo svojstvo aperiodičnosti koriste za generiranje velike površine neke teksture korištenjem malog broja početnih uzoraka, a da promatraču ne bude očito da je uzorak dobiven ponavljanjem manje slike. Pritom zbog uvjeta poklapanja oznaka na rubu uzorci glatko prelaze s pločice na pločicu, tj. prirodno se nastavljaju i ne vide se spojevi pločica. Neke primjere pokazat ćemo u 1. poglavlju. Osim toga, sposobnost Wangovih pločica da implementiraju Turingove strojeve, koji su modeli računala, pokušava se iskoristiti za izgradnju pravih računala, u kojima bi, kao u priči Wangovi sagovi, složene molekule (neke varijante DNA) i njihova biokemijska pravila slaganja implementirale Wangove pločice i provodile račune. Prednost takvih računala, ako ih se uspije realizirati, bila bi njihova veličina. Molekularno računalo, koliko god velike te molekule bile, bitno je manje od svih danas izradivih čipova. Do sada se pomoću molekula DNA na taj način uspjela implementirati jedna matematička operacija, XOR (ekskluzivni ili) na dva bita. Više o tome možete pročitati u [SE] i [W1].
Zamislite da pokušavate na računalu izraditi sliku neke velike površine zadane teksture, npr. mahovinu, polje tratinčica ili zvjezdano nebo. Nakon toga slika će postati dio neke računalne igre i htjet ćete, recimo, isprogramirati kako se tratinčice povijaju na vjetru, kako mahovina mijenja boju pri promjeni svjetla ili kako se ispred zvijezda kreće svemirski brod. Dok to radite, prirodnom se čini ideja da treba nekako iskoristiti činjenicu što su tratinčice prilično slične. Promatrač koji ih vidi stotinu vjerojatno neće uočiti da se na slici neka pojavila dvaput. Stoga bi trebalo biti dovoljno nacrtati samo nekoliko različitih tratinčica i zatim ponavljanjem na neki način generirati sliku s mnogo njih.

Prva i osnovna ideja je napraviti jednu pločicu i periodički je ponavljati. Međutim, ljudski mozak, koji radi tako da traži pravilnosti u svemu, vrlo brzo uočava takvo varanje. Već za mnogo jednostavniju sliku zvjezdanog neba postaje očito što smo napravili (jednostavniju jer zvijezde ipak izgledaju sličnije nego tratinčice, barem prostim okom):

Gornja slika ne izgleda prirodno jer se vidi da je dobivena periodičkim ponavljanjem malenog uzorka:

U članku [CO] Cohen, Shade, Hiller i Deussen opisali su metodu za rješavanje tog problema. Polazeći od malog uzorka teksture, njihov algoritam stvara skup od 18 Wangovih pločica. Slike na tim pločicama dobivene su pažljivim rezanjem danog uzorka i njegovim simetrijama da bi dobivene Wangove pločice bile različite, a na rubovima imale slike koje se nastavljaju (lijeva polovica tratinčice na desnom rubu pločice i desna polovica tratinčice na lijevom rubu susjedne pločice kao uvjet poklapanja koji zamjenjuje uvjet jednako obojenih rubova originalnih Wangovih pločica). Osim toga, oni postavljaju i dodatne uvjete, kojima se osigurava da se linije na kutovima pločica glatko nastavljaju. Ti "kutni uvjeti" mogli bi se zamijeniti dodavanjem uvjeta za rubove ako želimo biti sigurni da i dalje radimo s Wangovim pločicama. Nakon toga algoritam dobivenim pločicama neperiodično popločava traženi dio ravnine, dajući sliku koja, iako je nastala od malog broja elemenata, nema očitih ponavljanja. Sljedeća slika nastala je primjenom takvog algoritma na isti mali uzorak zvjezdanog neba prikazan na prethodnoj slici:

Nema očitih ponavljanja i slika djeluje mnogo prirodnije od one nastale periodičkim ponavljanjem, iako su obje nastale od istog malenog početnog uzorka.
Na web-stranici [BU] možete pronaći program koji implementira te ideje. U dani program, nakon instalacije, možete učitati svoju polaznu sliku i nakon toga vidjeti kako bi izgledale Wangove pločice složene od te slike i popločavanje njima. Gornje slike zvijezda nastale su upotrebom tog programa, a evo i slika tratinčica preuzetih iz članka [CO]:


Za potrebe izrade slika i grafike isti autori razvili su generalizaciju Wangovih pločica, Wangove kocke, kojima je moguće neperiodično popuniti prostor (ako npr. želite da se svemirski brod kreće među zvijezdama, a ne ispred njih).
Kao što je već spomenuto, pomoću Wangovih pločica može se implementirati Turingov stroj. Na početku se ulazni podaci postave u jedan red, a zatim se ravnina popločava red po red. Svaki sljedeći red kodira stanje trake nakon jednog koraka Turingovog stroja. Turingovi strojevi jedan su od osnovnih modela računala, koji jako dobro opisuju ono što želimo zvati "strojem za računanje". Jedna od definicija u teorijskom računarstvu glasi otprilike: problem je algoritamski rješiv ako se može riješiti Turingovim strojem. Drugim riječima, sve što se uopće može izračunati može se izračunati Turingovim strojem, pa stoga i Wangovim pločicama.
Ovdje ćemo pokazati nekoliko primjera računanja pomoću Wangovih pločica. Ovdje opisani načini nisu doslovne implementacije Turingovih strojeva jer ne provode račun "iz reda u red", popunjavajući jedan red ravnine za drugim kako se mijenja traka Turingovog stroja, nego nešto pojednostavljene verzije. Međutim, osnovne postavke ostaju iste - na određeno mjesto ravnine upisuju se ulazni podaci, a zatim se unaprijed zadane Wangove pločice slažu na jedini mogući način da bi se na kraju pločica koja kodira rješenje pojavila na točno određenom mjestu ravnine.
Primjer 2.1. Skup pločica koji zbraja dva prirodna broja a i b.
Račun ćemo provesti popločavanjem četvrtine ravnine, točnije prvog kvadranta. Pritom formalno možemo reći da popločavamo cijelu ravninu, a ostala tri kvadranta popuniti pločicama koje ne nose nikakvu informaciju. Kao što je vidljivo na donjoj slici, redovi i stupci će nam predstavljati prirodne brojeve, uključujući i nulu. Ulazne podatke a i b unijet ćemo tako da na mjesta (0,a) i (b,0) stavimo posebne pločice. Na donjoj slici vidimo ulazne podatke za popločavanje koje će zbrajati a=2 i b=4.
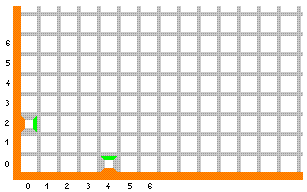
Računanje ćemo provesti pomoću sljedećeg skupa pločica:

Prve dvije pločice iz prvog reda već smo postavili - one su ulazni podaci. Da bismo ih lakše razlikovali od ostalih pločica u završnoj slici, obilježene su dodatno bijelim kvadratom u sredini i njih ne smijemo koristiti za popločavanje nakon što unesemo ulazne podatke. U gornjem računu postavljene su na mjesta (4,0) i (0,2), tj. želimo izračunati zbroj 2 + 4. Treća pločica iz prvog reda, označena crnim kvadratom u sredini, označava konačan rezultat - sumu tih brojeva. Pločice iz drugog reda koristimo za računanje, a četiri pločice u zadnjem redu ne nose nikakve informacije - one samo popunjavaju prazna mjesta u prvom kvadrantu (narančaste uz rub kvadranta, sive na ostalim mjestima).
Pokušajmo sada tim pločicama popločati kvadrant na slici iznad. Ako je ovo stvarno stroj za računanje, trebao bi postojati samo jedan način da to napravimo.
Prvo uočimo da desno od pločice na mjestu (0,2) možemo staviti samo neku pločicu koja ima lijevi rub obojen zeleno - dakle, drugu ili treću pločicu iz drugog reda. Ako stavimo treću pločicu, ispod nje mora doći pločica sa zeleno obojenim gornjim rubom, a takva je samo prva pločica u drugom redu (početne pločice više ne smijemo koristiti!) . Budući da je njezin donji rub također zelen, ispod nje bismo opet morali staviti jednu takvu. Tako bismo nastavili do donjeg ruba kvadranta, koji je narančast, i tu ne bismo mogli pronaći pločicu koja se uklapa. Dakle, mjesta (1,2), (2,2) itd. popunjavamo samo pločicom sa zelenim lijevim i desnim rubom. To je "prenošenje signala" zelenom bojom udesno.
Istom logikom zaključujemo da na mjesta iznad polja (4,0) smiju doći samo pločice sa zelenim gornjim i donjim rubom - "šaljemo signal" od ulaznog podatka prema gore. Tako nastavljamo sve dok se ta dva signala ne sretnu na polju (4,2), koje sada moramo popuniti pločicom sa zelenim donjim i lijevim rubom. Slika sada izgleda ovako:
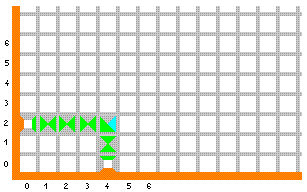
Plavi desni rub sada šalje novi "signal", prisiljavajući nas da naizmjenično stavljamo četvrtu i petu pločicu iz drugog reda sve dok ne dođemo do donje granice kvadranta, kad moramo staviti završnu pločicu za rezultat. Konačna slika izgleda ovako:
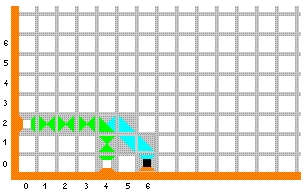
Završna pločica, koja označava izlaz računa, nalazi se na mjestu (6,0), što znači da je 2 + 4 = 6. Uočite da bi taj skup pločica na isti način za bilo koji ulaz a ≥ 1, b ≥ 1 dao izlaz a + b. Dakle, radi se zaista o skupu pločica za zbrajanje dvaju prirodnih brojeva. Da bi popločavanje bilo potpuno, treba još popuniti preostala bijela polja kvadranta pločicama iz trećeg reda (sivim i narančastim). Očito je da postoji samo jedan način da se to učini, pločicama koje ne nose informacije.
Zadatak 2.1. Što računa popločavanje četvrtog kvadranta pločicama na donjoj slici? Ulaznih podataka nema, a izlazni podaci obilježeni su pločicom s crnim kvadratom u sredini.
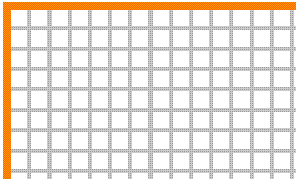
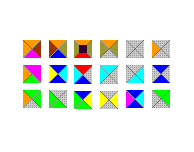
Zadatak 2.2. Konstruirajte skup Wangovih pločica koji računa zbroj dvaju cijelih brojeva popločavanjem poluravnine.
Primjer 2.2. Skup pločica koji množi dva prirodna broja a i b.
Množenje ćemo obaviti u desnoj poluravnini. Jednom pločicom obilježavamo koji red poluravnine smatramo x-osi (razina 0). Zatim ulazne podatke, brojeve a i b, unesemo tako da na mjesta (a,0) i (0,-b) stavimo odgovarajuće ulazne pločice (obilježene bijelim kvadratom). Te tri pločice smatrat ćemo ulaznima i nećemo ih koristiti u daljnjem popločavanju.

Koristit ćemo sljedeće pločice:

U prvom su redu tri ulazne pločice, jedna koja će obilježiti konačan rezultat i dvije "prazne pločice" bez informacija (jedna za mjesta uz rub poluravnine, jedna za ostala mjesta). Popunimo prvo gornju poluravninu. Uočite da koristimo samo pločice iz drugog i trećeg reda sa slike. To je zapravo popločavanje koje u prvom kvadrantu računa sve višekratnike od a:
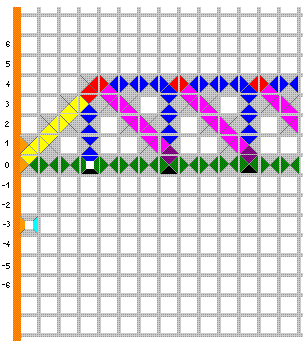
Vidimo da je jedini način popločavanja donje poluravnine sljedeći:
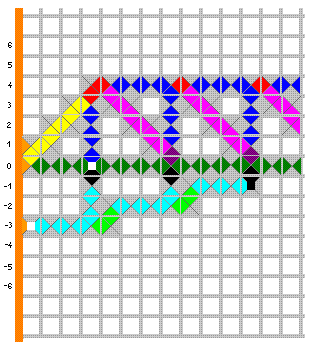
Sada bi još trebalo dodati pločice bez informacija, petu i šestu iz prvog reda, na prazna mjesta kako bismo zaista popločali cijelu poluravninu. U drugom dijelu računa koristili smo samo pločice iz trećeg reda. Ovaj "program" Wangovih pločica možemo shvatiti kao da se sastoji od dvaju potprograma koji se odvijaju uzastopno. Prvi prima ulaz a i u prvom kvadrantu računa višekratnike od a pomoću pločica iz drugog i trećeg reda, a drugi zatim za ulaz prima b i višekratnike od a te u četvrtom kvadrantu računa b-ti po redu višekratnik od a.
Zadatak 2.3. Konstruirajte skup Wangovih pločica koji računa zbroj ili umnožak dvaju prirodnih brojeva, ovisno o tome koja se od dviju pločica, S (suma) ili P (produkt), postavi u gornji lijevi kut četvrtog kvadranta. Ako treba, možete pretpostaviti da su a i b različiti brojevi veći od 1.
Zadatak 2.4. Konstruirajte skup Wangovih pločica koji računa članove niza 1, 4, 9, 16, 25... (kvadrate prirodnih brojeva).
Ilustrirat ćemo Wangov (kako smo vidjeli, neuspješan) pokušaj konstrukcije algoritma za provjeru može li se danim konačnim skupom Wangovih pločica popločati ravnina, dokazati neke rezultate koji su mu trebali u tim pokušajima i objasniti što ga je navelo da postavi hipotezu o nepostojanju aperiodičnih skupova.
Dokažimo prvo Wangov teorem:
Ako nekim konačnim skupom Wangovih pločica možemo popločati proizvoljno velike kvadrate, onda tim skupom pločica možemo popločati cijelu ravninu.
Drugim riječima, ako za svaki prirodan broj n možemo popločati n×n kvadrat, onda možemo popločati i ravninu. Uočite da je obrat trivijalan: ako možemo popločati ravninu, onda možemo i kvadrate bilo koje veličine (ravnina sadrži proizvoljno velike popločane kvadrate). Isto tako, ako možemo popločati neki kvadrat, možemo popločati i sve kvadrate manje od njega.
Dokaz. Popločavanja kvadrata iz iskaza teorema organizirat ćemo u stablo s korijenom. To je poseban slučaj grafa. Svaki graf sastoji se od nekog skupa vrhova, od kojih su neki povezani bridovima. Posebnost je korijenskog stabla što je povezano (od svakog vrha može se, idući bridovima, doći do svakog drugog), što nema ciklusa (ne može se, idući bridovima, napraviti krug) i što ima jedan istaknuti vrh koji smatramo korijenom. Zbog tih svojstava korijenskog stabla za svaki vrh možemo odrediti koliko je daleko od korijena; budući da nema ciklusa, postoji jedinstveni put od svakog vrha do korijena. Na taj način sve vrhove možemo podijeliti na nivoe: na nultom nivou nalazi se korijen, na prvom nivou oni vrhovi koji su za jedan brid udaljeni od korijena, na drugom nivou oni koji su za dva brida udaljeni od korijena i tako dalje.
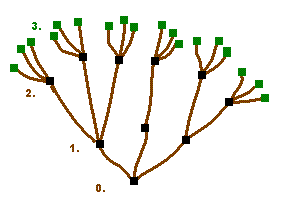
Opišimo prvo vrhove našeg stabla. Na nultom nivou nalazi se samo jedan vrh, korijen. Svaki vrh na prvom nivou predstavlja jednu od Wangovih pločica koje smijemo koristiti u popločavanju. Svaki vrh na drugom nivou predstavlja jedno popločavanje 3×3 kvadrata Wangovim pločicama koje smijemo koristiti; svaki vrh na trećem nivou jedno 5×5 popločavanje i tako dalje. Općenito, vrhovi na n-tom nivou predstavljaju sva moguća popločavanja (2n-1)×(2n-1) kvadrata. Uočite da nijedan nivo nije prazan (jer za svaku veličinu kvadrata postoji popločavanje) i da se na svakom nivou nalazi konačno mnogo vrhova (jer imamo konačan skup pločica). Međutim, cijelo stablo ima beskonačno mnogo vrhova jer nivoa ima beskonačno mnogo.
Da bismo do kraja opisali stablo, moramo još reći koji su vrhovi povezani bridovima. Korijen je povezan sa svim vrhovima na prvom nivou. Vrh na n-tom nivou, koji predstavlja popločavanje kvadrata stranice 2n-1, povezan je s nekim vrhom na (n+1)-vom nivou, koji predstavlja popločavanje kvadrata stranice 2n+1, ako se popločavanje većeg kvadrata može dobiti iz popločavanja manjeg tako da se manji okruži po jednim redom pločica sa svake strane (poštujući, naravno, pravila slaganja Wangovih pločica). Ostale vrhove ne povezujemo.
Sada konstruiramo put u grafu. Za početni vrh odaberemo korijen. Vrhove dalje biramo induktivno: ako smo u prethodnom koraku odabrali vrh v na n-tom nivou, u sljedećemo biramo vrh na (n+1)-vom nivou koji je povezan s vrhom v i takav da postoji beskonačno mnogo vrhova na nivoima iznad njega koji su s njim povezani. Takav izbor uvijek možemo napraviti: ako je iznad vrha v bilo beskonačno mnogo vrhova, a na nivou neposredno iznad samo konačno mnogo, onda ih se nad nekima od tih konačno mnogo mora nalaziti beskonačno (inače bi ih ukupno bilo konačno). Tako dobivamo beskonačan put po stablu s po jednim vrhom na svakom nivou. Ta tvrdnja se u teoriji grafova zove Köningova lema.
Promotrimo što smo učinili izborom takvog puta. Odabrali smo jednu pločicu (prvi nivo), takvu da oko nje možemo postaviti pločice i dobiti popločavanje 3×3 kvadrata (drugi nivo). Oko njega možemo postaviti pločice i dobiti popločavanje 5×5 kvadrata (treći nivo) i tako dalje. Beskonačnost puta osigurava da nećemo "zapeti" u popločavanju, tj. da možemo stalno dodavati još jedan red pločica oko već popločanog kvadrata. Drugim riječima, možemo popločati cijelu ravninu. Time je teorem dokazan. ■
Pretpostavka o konačnosti skupa pločica bila je pritom bitna. Naime, Köningova lema vrijedi samo uz pretpostavku da se na svakom nivou nalazi konačno mnogo vrhova. Protuprimjer je stablo koje na svakom nivou ima beskonačno mnogo vrhova, označenih prirodnim brojevima. Vrh označen brojem i ≥ 2 na n-tom nivou povezan je s vrhom označenim brojem i-1 na (n+1)-vom, a vrh označen brojem 1 nije povezan ni s jednim vrhom na sljedećem nivou. U tom stablu nema beskonačno dugačkih puteva. To još ne znači da teorem ne vrijedi i za beskonačne skupove Wangovih pločica (možda bismo samo trebali potražiti neki drugi dokaz), ali lako je pronaći protuprimjer. Promotrimo popločavanje četvrtine ravnine kvadratima i obojimo rubove tih kvadrata s beskonačno mnogo različitih boja - tako da se svaka boja pojavljuje samo na po jednom rubu dviju susjednih pločica i nigdje drugdje. S takvim pločicama očito je moguće popločati proizvoljno velik kvadrat, ali ne i cijelu ravninu.
Znajući teorem, Wang je promatrao ovakav algoritam za ispitivanje može li se zadanim skupom Wangovih pločica popločati ravnina:
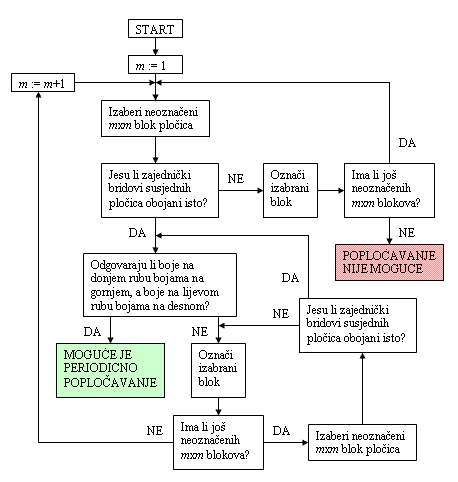
Za prirodne brojeve m = 1, 2, 3... provjeravamo sve m×m kvadrate sastavljene od pločica iz zadanog skupa, poštujući pravila slaganja. Ako za neki m ne postoji nijedan takav kvadrat, ravnina se ne može popločati tim skupom pločica i algoritam završava. Ako pak pronađemo neki kvadrat kojim možemo periodično popločati ravninu, algoritam također staje. Uočite da vrijede i obrati tih tvrdnji: ako se ravnina ne može popločati, po Wangovom teoremu postoji prirodan broj m takav da se ne može popločati ni m×m kvadrat. Ako se pak ravnina može popločati periodično, tako da se uzorak horizontalno ponavlja svakih m, a vertikalno svakih n pločica, tada se može periodično popločati kvadratom veličine m·n i algoritam će također stati nakon konačno mnogo koraka.
Problem nastaje ako se mogu popločati sve veći i veći kvadrati a da se nikad ne pojavi periodičnost. U tom slučaju algoritam nikada ne staje, tj. ne daje odgovor. To je točno slučaj kad je zadani skup pločica aperiodičan i navelo je Wanga da postavi hipotezu o nepostojanju aperiodičnih skupova pločica. Hipoteza se pokazala krivom - algoritam kakav je Wang pokušao konstruirati 1961. ne postoji, a problem popločavanja ravnine je neodlučiv!
Na kraju ovog poglavlja navest ćemo još dvije posljedice Wangovog teorema.
Pretpostavimo da je neki skup S Wangovih pločica minimalan, tj. da njime možemo popločati ravninu, ali bilo kojim njegovim pravim podskupom ne možemo. Tada postoji prirodan broj n takav da se u svakom popločavanju ravnine tim skupom pločica i u svakom n×n bloku pločica tog popločavanja nalaze sve pločice skupa S.
Pretpostavimo da je S skup Wangovih pločica kojim možemo popločati ravninu. Tada za svaki prirodan broj n postoji popločavanje ravnine tim skupom pločica takvo da se svaki n×n blok pločica koji se pojavljuje u tom popločavanju, pojavljuje u njemu beskonačno mnogo puta.
Zadatak 3.1. Dokažite te tvrdnje!
Ako promatramo kako se od 1966. godine, kad je otkriven prvi aperiodičan skup Wangovih pločica, smanjivao broj pločica u najmanjem poznatom skupu, primjećujemo da su se važna smanjenja događala uvođenjem neke potpuno nove ideje za konstrukciju skupa pločica. Prva, Bergerova ideja, bila je oponašanje dokaza neodlučivosti problema zaustavljanja Turingovog stroja. Modifikacije te ideje dovele su do smanjivanja s 20462 na 104 i 92 pločice. Sljedeća smanjenja došla su tek s novim idejama, kad su Robinson i Penrose modificirali neka druga u međuvremenu otkrivena aperiodična popločavanja ravnine da bi od njih dobili Wangove pločice (Penroseovo popločavanje dvjema pločicama u obliku romba s obilježenim stranicama i vrhovima). Posljednje smanjenje dogodilo se 1995., kad je Jarkko Kari u članku [KA] opisao kako se množenje realnog broja racionalnima može prvo opisati konačnim automatima, a zatim se te konačne automate može kodirati u Wangove pločice i tako dobiti beskonačno mnogo aperiodičkih popločavanja ravnine. Tu njegovu ideju malo je doradio Karel Culik i u članku [CU] konstruirao aperiodičan skup od 13 Wangovih pločica s 5 boja. Ovdje ćemo opisati taj skup i navesti osnovne ideje dokaza.
Koristit ćemo zapis realnog broja pomoću niza cijelih brojeva beskonačnog s obiju strana, tj. indeksiranog cijelim brojevima. Niz dobivamo na sljedeći način: za realan broj r prvo definiramo niz A(r,i), indeksiran cijelim brojevima i, sa A(r,i) = najveće cijelo broja i·r. Najveće cijelo realnog broja x je najveći cijeli broj manji ili jednak od x. Dobili smo niz cijelih brojeva pomoću kojeg ćemo definirati novi niz, također indeksiran cijelim brojevima:
Može se pokazati da se niz B(r,i) sastoji od najviše dvaju cijelih brojeva. Točnije, ako je k ≤ r ≤k+1, onda se u nizu B(r,i) pojavljuju samo brojevi k i k+1. Nadalje, svaki niz brojeva k i k+1 određuje neki realan broj r: ako računamo zbroj bilo kojih n uzastopnih elemenata, on će se od broja n·r razlikovati za manje od 1, a prosjek n uzastopnih elemenata približavat će se r kada n raste. Niz B(r,i) je, dakle, zaista zapis realnog broja r, u smislu da postoji bijekcija između skupa realnih brojeva i takvih nizova cijelih brojeva.
Zadatak 4.1. Izračunajte sve članove nizova B(1,i), B(3/2,i), B(1/3,i) i B(8/3,i)!
Promatrajući kako se broj u takvom zapisu množi s 3 i s 1/2, Culik je došao do sljedećeg skupa pločica T:
| T3 | 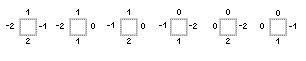 |
| T1/2 | 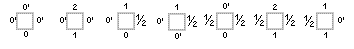 |
Pločice iz gornjeg reda čine podskup označen s T3, koji oponaša množenje s 3. Pločice iz donjeg reda čine podskup T1/2 za množenje s 1/2. Znak 0′ u drugom redu označava broj 0; crtica je dodana samo zato da osiguramo da se pločice iz T3 i T1/2 moraju staviti u različite redove prilikom popločavanja. Pločice iz skupa T imaju sljedeća svojstva:
Navedene tvrdnje nećemo dokazivati. Detalji dokaza uključuju konačne automate i nešto malo aritmetike i možete ih pogledati u člancima [KA] i [CU]. Međutim, koristeći se tim tvrdnjama dokazat ćemo da je skup pločica T uistinu aperiodičan.
Gore opisanim skupom pločica T ravnina se može popločati, ali ne periodično.
Dokaz. Neka je r bilo koji realan broj iz intervala [1/3,2]. Popločimo jedan redak ravnine pločicama iz skupa T tako da oznake na gornjoj strani tvore zapis broja r. Znamo da redak možemo popločati poločicama iz T3 ako je r iz intervala [1/3,2/3], a pločicama iz T1/2 ako je r iz [2/3,2]. U prvom slučaju znamenke na donjoj strani retka tvore zapis broja 3r, koji je iz intervala [1,2], a u drugom slučaju tvore zapis broja r/2, koji je iz intervala [1/3,1]. Svakako je sada na donjoj strani retka ponovno zapis nekog broja iz intervala [1/3,2], koji ponovno kodiramo u sljedećem retku ravnine (oznake na horizontalnim rubovima moraju se poklapati!). Tako nastavljamo postupak, popunjavajući redak po redak ravnine prema dolje.
Što se tiče gornje polovice ravnine, možemo primijeniti isti postupak, ali obrnuto. Za realan broj r iz [1/3,2] kodiran na gornjoj strani retka sigurno postoji neki broj p iz istog intervala tako da je r = 3p ako je r iz intervala [1,2], odnosno r = p/2 ako je r iz [1/3,1]. Ako sada broj p kodiramo novim retkom, oznake na donjoj strani tvorit će zapis broja r, tj. poklapat će se s oznakama na gornjoj strani prethodnog retka. To znači da opisanim postupkom možemo redak po redak popločati i gornju polovicu ravnine.
Uočite da smo za svaki realan broj iz intervala [1/3,2] dobili jedno popločavanje. Neka od tih popločavanja su ista, točnije, ako se broj r′ nalazi u k-tom retku popločavanja dobivenog od broja r, onda se popločavanje koje dobijemo krenuvši od r′ podudara s prvim popločavanjem translatiranim vertikalno za k. Međutim, različitih popločavanja dobivenih na ovaj način ipak ima neprebrojivo mnogo jer se od svakog translacijama može dobiti samo prebrojivo mnogo popločavanja.
Konačno, treba dokazati da nijedno popločavanje gornjim skupom pločica nije periodično. Kad bi bilo, onda bi postojao prirodan broj k takav da vertikalna translacija za k prevodi popločavanje samo u sebe. To bi značilo da su brojevi koje kodira gornja strana prvog i (k+1)-vog retka isti. Znamo da je broj kodiran u (k+1)-vom retku dobiven od broja u prvom retku s nekoliko uzastopnih množenja brojevima 3 i 1/2. To bi značilo da se s nekoliko uzastopnih množenja brojeva 3 i 1/2 može dobiti 1, što je očito nemoguće. Time je teorem dokazan.■
Rubovi pločica iz skupa T označeni su brojevima. Ako ih želimo zamijeniti minimalnim brojem boja, možemo primijetiti da, budući da ne smijemo okretati pločice, nema potrebe razlikovati oznake na horizontalnim i vertikalnim bridovima pločica. Ti bridovi nikad ne mogu doći u kontakt pa različito bojanje ne predstavlja dodatni uvjet. Budući da na vertikalnim bridovima ima pet različitih oznaka, a na horizontalnim četiri, sve ih možemo zamijeniti s max{4,5} = 5 boja. Na taj je način dobiven aperiodičan skup pločica na ranije prikazanoj slici.
| [BU] | R. Burke, Image quilting, Wang tiling, and texture transfer. http://www.heroicsalmonleap.net/mle/wang/index.html |
| [CO] | M.F. Cohen, J. Shade, S. Hiller, O. Deussen Wang Tiles for Image and Texture Generation, Siggraph 2003, San Diego. |
| [CU] | K. Culik, An aperiodic set of 13 Wang tiles, Discrete Mathematics 160 (1996), 245-251. |
| [EG] | G. Egan, Wangovi sagovi, Math.e 8 (2006). http://web.math.hr/mathe/sagovi |
| [GR] | B. Grünbaum, G.C. Shepard, Tilings and Patterns, W.H. Freeman and Company, New York, 1987. |
| [KA] | J. Kari, A small aperiodic set of Wang tiles, Discrete Mathematics 160 (1996), 259-264. |
| [KR] | K. Krulić, Popločavanja ravnine, Math.e 7 (2006). http://web.math.hr/mathe/poplocavanja |
| [SE] | N. Seeman, DNA-based computation and algorithmic assembly. http://seemanlab4.chem.nyu.edu/XOR.html |
| [WI] | Wikipedia: The Free Encyclopedia (lipanj 2006.), Wang tile. http://en.wikipedia.org/wiki/Wang_tile |
| [W1] | E. Winfree, DNA computing by self-assembly, The Bridge 33 (2003), 31-38. |
| [W2] | E. Winfree, Algorithmic self-assembly of DNA: theoretical motivations and 2D assembly experiments, Journal of Biomolecular Structure & Dynamics, Conversation 11, No. 2 (2000), 263-270. |
0. Uvod
1. Crtanje pomoću Wangovih pločica
2. Računanje pomoću Wangovih pločica
3. Neodlučivost problema popločavanja
4. Jedan aperiodičan skup Wangovih pločica
Literatura