
Hrvatski matematički elektronski časopis math.e

|
Hrvatski matematički elektronski časopis math.e |
| http://www.math.hr/~mathe/ |
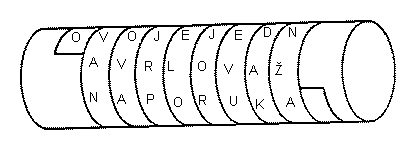 Neki elementi kriptografije naziru se već kod starih Grka.
Naime, Spartanci su već u 5. stoljeću prije Krista
u vojne svrhe upotrebljavali
napravu za šifriranje zvanu skital. To je bio drveni štap oko kojega se
namotavala vrpca od pergamenta na koju se uzdužno pisala poruka.
Nakon upisivanja poruke vrpca bi se odmotala, a na njoj bi ostali
izmiješani znakovi koje je mogao pročitati samo onaj tko je
imao štap jednake debljine.
Neki elementi kriptografije naziru se već kod starih Grka.
Naime, Spartanci su već u 5. stoljeću prije Krista
u vojne svrhe upotrebljavali
napravu za šifriranje zvanu skital. To je bio drveni štap oko kojega se
namotavala vrpca od pergamenta na koju se uzdužno pisala poruka.
Nakon upisivanja poruke vrpca bi se odmotala, a na njoj bi ostali
izmiješani znakovi koje je mogao pročitati samo onaj tko je
imao štap jednake debljine.
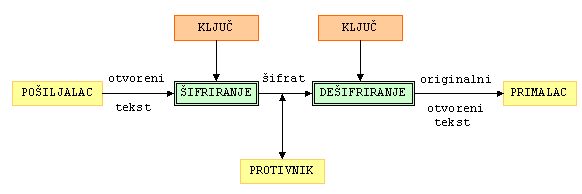
Osnovni zadatak kriptografije je omogućavanje dvjema osobama (zvat ćemo ih pošiljalac i primalac) da komuniciraju preko nesigurnog komunikacijskog kanala na način da treća osoba (njihov protivnik) ne može razumjeti njihove poruke. Poruku koju pošiljalac želi poslati primaocu zovemo otvoreni tekst. To može biti tekst na njihovom materinjem jeziku, numerički podatci ili bilo što drugo. Pošiljalac transformira otvoreni tekst koristeći unaprijed dogovoreni ključ. Taj postupak zove se šifriranje, a dobiveni rezultat šifrat ili kriptogram. Nakon toga pošiljalac pošalje šifrat preko nekog komunikacijskog kanala. Protivnik prisluškujući može doznati sadržaj šifrata, ali ne može odrediti otvoreni tekst. Za razliku od njega, primalac koji zna ključ kojim je šifrirana poruka može dešifrirati šifrat i odrediti otvoreni tekst.
Kriptografski algoritam ili šifra je matematička funkcija koja se koristi za šifriranje i dešifriranje. Općenito, radi se o dvjema funkcijama, jednoj za šifriranje (njezini argumenti su ključ i otvoreni tekst), a drugoj za dešifriranje (njezini argumenti su ključ i šifrat). Skup svih mogućih vrijednosti ključeva zovemo prostor ključeva. Kriptosustav se sastoji od kriptografskog algoritma, te svih mogućih otvorenih tekstova, šifrata i ključeva.
Funkcije šifriranja i dešifriranja koje odgovaraju ključu K označavat ćemo s eK, odnosno dK. One su jedna drugoj inverzne. Kriptosustave kod kojih je iz poznavanja funkcije eK lako izračunati funkciju dK nazivamo simetrični kriptosustavi. Njihova sigurnosti leži u tajnosti ključa. Dakle, pošiljalac i primalac moraju prije same komunikacije tajno razmijeniti ključ. Kako im nije dostupan "sigurni komunikacijski kanal" (jer inače ne bi ni imali potrebu za šifriranjem poruka), ovo može biti veliki problem.
Postoje i asimetrični kriptosustavi ili kriptosustavi s javnim ključem. Kod njih se za šifriranje koriste funkcije eK koje su "jednosmjerne" (one se računaju lako, ali njihov inverz vrlo teško). To znači da funkcija za šifriranje eK može biti javna, dok samo funkcija za dešifriranje dK mora biti tajna. Kako su ovakvi kriptosustavi mnogo sporiji od najboljih simetričnih kriptosustava, u praksi se kriptosustavi s javnim ključem koriste za sigurnu razmjenu ključeva koji se potom koriste u šifriranju poruke nekim simetričnim kriposustavom. U ovom članku nećemo se baviti kriptosustavima s javnim ključem. Recimo ipak da se svi oni zasnivaju na teškim matematičkim problemima. Jedan od njih je faktorizacija velikih prirodnih brojeva. Naime, mnogo je lakše pomnožiti dva broja nego njihov umnožak rastaviti na faktore. Uvjerite se u to i sami rješavajući sljedeća dva zadatka:
 Znameniti rimski vojskovođa i državnik
Julije Cezar u
komunikaciji sa svojim prijateljima koristio se sa šifrom u kojoj
su se slova otvorenog teksta zamjenjivala slovima što su se u alfabetu
nalazila tri mjesta dalje od njih
(A
Znameniti rimski vojskovođa i državnik
Julije Cezar u
komunikaciji sa svojim prijateljima koristio se sa šifrom u kojoj
su se slova otvorenog teksta zamjenjivala slovima što su se u alfabetu
nalazila tri mjesta dalje od njih
(A 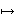 D,
B
D,
B 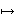 E, ... ,
Z
E, ... ,
Z 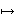 C).
Ako bismo upotrijebili današnji engleski alfabet od 26 slova, onda
bi poznata izreka
C).
Ako bismo upotrijebili današnji engleski alfabet od 26 slova, onda
bi poznata izreka
VENI VIDI VICI
bila šifrirana ovako:YHQL YLGL YLFL.
Cezarovu šifru možemo pregledno zapisati na sljedeći način:otvoreni tekst A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
šifrat D E F G H I J K L M N O P Q R S T U V W X Y Z A B C
Najpoznatije klasične supstitucijske šifre definiraju se nad
engleskim (međunarodnim) alfabetom od 26 slova. Pritom se u definiciji
često koristi ova korespondencija između slova alfabeta i skupa
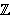
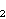
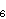 = {0, 1, 2, ... , 25}:
= {0, 1, 2, ... , 25}:
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25U skladu s tim, ako budemo radili s otvorenim tekstom na hrvatskom jeziku, onda ćemo Č i Ć zamijeniti s C, a Đ, Dž, Lj, Nj, Š, Ž redom s DJ, DZ, LJ, NJ, S, Z.
Na skupu
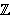
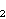
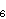 možemo definirati zbrajanje modulo 26 na sljedeći način:
a + b mod 26 je ostatak pri dijeljenju broja a + b s 26.
možemo definirati zbrajanje modulo 26 na sljedeći način:
a + b mod 26 je ostatak pri dijeljenju broja a + b s 26.
Danas se Cezarovom šifrom nazivaju i šifre istog oblika s pomakom različitim od 3. Dakle, Cezarovu šifru možemo definirati na sljedeći način:
Za x, y, K
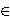
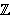 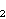 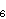 definiramo
definiramo
eK(x) = x + K mod 26,
dK(y) = y
|
Očito je dK(eK(x)) = x, kao što se i zahtjeva u definiciji kriptosustava. Za K = 3 dobiva se originalna Cezarova šifra.
Primjer 1: Dekriptirajte šifrat NXBGZYQG dobiven Cezarovom šifrom.
Budući da je prostor ključeva vrlo malen (ima ih 26), zadatak možemo riješiti "grubom silom", tj. tako da ispitamo sve moguće ključeve dok ne dođemo do nekog smislenog teksta. Za d0, d1, ... dobivamo redom:
N X B G Z Y Q G M W A F Y X P F L V Z E X W O E K U Y D W V N D J T X C V U M C I S W B U T L B H R V A T S K ADakle, ključ je K = 6, a otvoreni tekst je HRVATSKA.
Cezarova šifra je poseban slučaj supstitucijske šifre koja je definirana s:
Neka su x, y 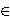
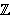 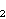 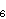 .
Za svaku permutaciju .
Za svaku permutaciju 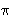 skupa {0, 1, 2, ... , 25} definiramo
skupa {0, 1, 2, ... , 25} definiramo
e 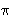 -1
inverzna permutacija od -1
inverzna permutacija od 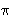 . .
|
Ovdje imamo 26! 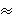 4
4
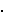 1026 mogućih ključeva,
tako da je napad ispitivanjem svih mogućih ključeva
praktički nemoguć čak i uz pomoć računala.
Međutim, supstitucijsku šifru lako je moguće dekriptirati
koristeći neka statistička svojstva jezika na kojemu je pisan
otvoreni tekst. Osnovna metoda je analiza frekvencije slova;
broji se pojavljivanje svakog slova u šifratu, te se distribucija
slova u šifratu uspoređuje s poznatim podatcima o distribuciji
slova u jeziku otvorenog teksta. Vrlo je vjerojatno da najfrekventnija
slova šifrata odgovaraju najfrekventnijim slovima jezika.
Ta vjerojatnost raste s duljinom šifrata. Također mogu biti korisni
i podatci o najčešćim bigramima (parovima slova) i
trigramima (nizovima od tri slova) u jeziku.
1026 mogućih ključeva,
tako da je napad ispitivanjem svih mogućih ključeva
praktički nemoguć čak i uz pomoć računala.
Međutim, supstitucijsku šifru lako je moguće dekriptirati
koristeći neka statistička svojstva jezika na kojemu je pisan
otvoreni tekst. Osnovna metoda je analiza frekvencije slova;
broji se pojavljivanje svakog slova u šifratu, te se distribucija
slova u šifratu uspoređuje s poznatim podatcima o distribuciji
slova u jeziku otvorenog teksta. Vrlo je vjerojatno da najfrekventnija
slova šifrata odgovaraju najfrekventnijim slovima jezika.
Ta vjerojatnost raste s duljinom šifrata. Također mogu biti korisni
i podatci o najčešćim bigramima (parovima slova) i
trigramima (nizovima od tri slova) u jeziku.
Začetci analize frekvencija mogu se naći u 14. stoljeću u djelu arapskog autora Ibn ad-Duraihima, a čini se da su tu metodu u isto vrijeme poznavali i talijanski kriptografi.
Navest ćemo osnovne podatke za hrvatski jezik. Pritom smatramo da u tekstu nema interpunkcijskih znakova ni razmaka između riječi (u protivnom bi kriptoanaliza bila mnogo lakša), te da su slova Č, Ć, Đ, Dž, Lj, Nj, Š, Ž iz hrvatske abecede zamijenjena na ranije opisani način slovima iz međunarodnog alfabeta.
| FREKVENCIJA SLOVA (u promilima) | |||||
| A | 115 | K | 36 | ||
| I | 98 | V | 35 | ||
| O | 90 | L | 33 | ||
| E | 84 | M | 31 | ||
| N | 66 | P | 29 | ||
| S | 56 | C | 28 | ||
| R | 54 | Z | 23 | ||
| J | 51 | G | 16 | ||
| T | 48 | B | 15 | ||
| U | 43 | H | 8 | ||
| D | 37 | F | 3 | ||
Spomenimo da su najfrekventnija slova u engleskom jeziku
E, T, A, O, I, N, S, R, H, L.
U njemačkom jeziku to su
E, N, I, R, S, A, T, D, H, U, a u francuskom
E, A, I, S, T, N, R, U, L, O.
Najfrekventniji bigrami u hrvatskom jeziku su:
JE (2.7 %), NA (1.5 %), RA (1.5 %), ST, AN, NI, KO, OS, TI, IJ, NO, EN, PR (1.0 %).
Ovdje je korisno uočiti da je JE najfrekventniji bigram, iako J nije među najfrekventnijim slovima. Više od pola pojavljivanja slova J otpada na bigram JE. Druga zanimljivost je da su svi najfrekventniji bigrami oblika suglasnik-samoglasnik ili samoglasnik-suglasnik, osim bigrama ST i PR. Konačno, najfrekventniji recipročni bigrami su NA i AN (1.5 % + 1.4 %), te NI i IN (1.3 % + 0.9 %). Jedino su kod ovih dvaju parova frekvencije obaju bigrama veće od 0.9 %.Daleko najfrekventniji trigram u hrvatskom jeziku je IJE (0.6 %). Slijede (s frekvencijama između 0.3 % i 0.4 %): STA, OST, JED, KOJ, OJE, JEN.
U engleskom jeziku najfrekventniji bigrami su
TH, HE, AN, IN, ER, RE, ON, ES, TI, AT,
a trigrami THE, ING, AND, ION, TIO.Primjer 2: Treba dekriptirati šifrat
TQCWT QCKIQ RWNOQ OBCEW OQVKB UKAPK OQOQB CQPQA JGDUQ EQORW TSJGR WEQKY WGTWC JKRBI KZGVO GBQdobiven supstitucijskom šifrom, ako je poznato da je otvoreni tekst na hrvatskome jeziku.
Analizu frekvencija slova i bigrama možemo izvršiti pomoću tablice u kojoj pokraj svakog slova zapisujemo sve njegove sljedbenike u šifratu. Iz tablice iščitavamo da su najfrekventnija slova u šifratu:
Q (13), K (7), O (7), W (7), B, C, G, R, T, E, J,
dok su najfrekventniji bigrami:OQ (4), QO (3), RW (3), BC, EQ, JG, QC, TQ, WT.
Logično je pretpostaviti da je e(A) = Q. Također uočavamo recipročne bigrame OQ i QO, što nas vodi do zaključka da je vjerojatno e(N) = O. Uočavamo da je većina pojavljivanja slova R vezana uz bigram RW, te da je W jedno od najfrekventnijih slova u šifratu. To nas pak vodi do pretpostavke da je e(J) = R i e(E) = W. Pokušajmo otkriti šifrat čestog bigrama ST (najčešćeg od neotkrivenih). Najozbiljniji kandidati su BC i JG. Možemo uzeti neki od njih pa vidjeti što ćemo dobiti. Krenut ćemo s BC jer frekvencije od B i C odgovaraju očekivanim frekvencijama od S i T. Dakle, uzmimo da je e(S) = B i e(T) = C. Od najfrekventnijih slova u hrvatskom jeziku još nismo odgonetnuli šifrate od I i O. Glavni kandidati su K i G, i to upravo u tom redoslijedu. Uzmimo da je e(I) = K i e(O) = G. Rezimirajmo ono što smo do sada pretpostavili:
otvoreni tekst A B C D E F G H I J K L M N O P Q R S T U W X Y Z
šifrat q w k r o g b c
Ubacimo ove pretpostavke u polazni šifrat:
TQCWT QCKIQ RWNOQ OBCEW OQVKB UKAPK ate ati a je na nst e na is i i OQOQB CQPQA JGDUQ EQORW TSJGR WEQKY nanas ta a o a anje oj e ai WGTWC JKRBI KZGVO GBQ eo et ijs i o n osaSada već imamo dovoljno elemenata otvorenog teksta da možemo postupno odgonetavati čitave riječi (npr. prva riječ: MATEMATIKA; zadnja riječ: ODNOSA). Konačno dobivamo otvoreni tekst
Matematika je znanstvena disciplina nastala proučavanjem brojeva i geometrijskih odnosaAlfabet šifrata izgleda ovako:
q s u v w x y z k r i p t o g a f j b c d e h l m nDakle, ovo nije bilo kakva supstitucijska šifra, nego jedna vrlo specijalna šifra koja se naziva Cezarovom šifrom s ključnom riječi. U njoj ključ predstavlja ključna riječ (u ovom slučaju KRIPTOGRAFIJA), te broj (u ovom slučaju 8) koji označava poziciju na kojoj počinjemo pisati ključnu riječ (bez ponavljanja slova). Jasno, da smo znali da je riječ upravo o ovoj varijanti, dekriptiranje bi nam bilo još lakše, no i bez toga nismo imali mnogo problema.
Prema tome, usprkos velikom prostoru ključeva, supstitucijska šifra je vrlo laka za kriptoanalizu. To je bilo poznato već početkom 15. stoljeća, kada je u Italiji počela uporaba tzv. homofona, tj. šifriranje najfrekventnijih slova s više različitih simbola. To svakako povećava sigurnost šifre, ali i dalje se analizom frekvencija bigrama i trigrama može doći do rješenja.

Kod supstitucijske šifre svakom slovu otvorenog teksta odgovara jedinstveno slovo šifrata. Takvi kriptosustavi zovu se monoalfabetski. Sada ćemo prikazat Vigenèreovu šifru koja pripada polialfabetskim kriptosustavima. Naime, kod nje se svako slovo otvorenog teksta može preslikati u jedno od m mogućih slova (gdje je m duljina ključa).
Blaise de Vigenère je 1586. godine objavio knjigu u kojoj se nalazilo sve što se u to vrijeme znalo o kriptografiji. U njoj je opisano više originalnih polialfabetskih sustava. Sustav koji se danas naziva Vigenèreova šifra definiran je s:
|
Neka je m fiksan prirodni broj.
Za ključ K = (k1, k2,
... , km) definiramo
eK(x1, x2, ... ,
xm) = (x1 + k1,
x2 + k2, ... ,
xm + km), 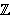 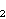 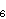 . .
|
Primjer 3: Neka je m = 4, a ključna riječ BROJ. Njezin numerički ekvivalent je ključ K = (1, 17, 14, 9). Pretpostavimo da je otvoreni tekst KRIPTOLOGIJA. Šifriranje se provodi na sljedeći način:
10 17 8 15 19 14 11 14 6 8 9 0
1 17 14 9 1 17 14 9 1 17 14 9
+26 _________________________________________________________
11 8 22 24 20 5 25 23 7 25 23 9
Dakle, šifrat je LIWYUFZXHZXJ.
Rezultat možete provjeriti i OVDJE:
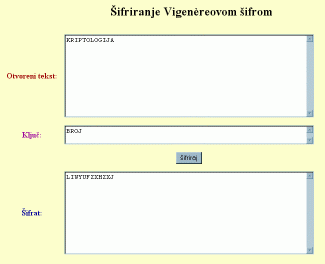
Primjer 3 može se ilustrirati ovako:
ključ B R O J B R O J B R O J
otvoreni tekst K R I P T O L O G I J A
šifrat L I W Y U F Z X H Z X J
Vidimo da se ovdje ključ ponavlja u nedogled. Postoje i druge
varijante Vigenèreove šifre.
Jedna takva (sigurnija od originalne)
je ona s autoključem, u kojoj otvoreni tekst generira ključ.
Primjer 4: Sve isto kao u Primjeru 3, ali s autoključem.
U šifriranju ćemo koristiti tzv. Vigenèreov kvadrat. (Ako slovo K treba šifrirati ključem B, onda pogledamo stupac koji počinje s K i redak koji počinje s B. U presjeku je šifrat L.)
ključ B R O J K R I P T O L O
otvoreni tekst K R I P T O L O G I J A
šifrat L I W Y D F T D Z W U O
Vigenèreova šifra jedan je od najpopularnijih kriptosustava u povijesti. Spomenimo da je korištena tijekom američke revolucije, krajem 18. stoljeća. Godine 1917. u uglednom časopisu "Scientific American" objavljeno je da je ovu šifru "nemoguće razbiti". To, naravno, nije bilo točno jer su kriptoanalitičari već pola stoljeća prije toga poznavali metode za napad na Vigenèreovu šifru.
Recimo sada nešto o kriptoanalizi Vigenèreove šifre.
Prvi korak je određivanje duljine ključne riječi. Prikazat ćemo dvije metode. Prva metoda zove se Kasiskijev test i uveo ju je Friedrich Kasiski 1863. godine. Metoda se zasniva na činjenici da će dva identična odsječka otvorenog teksta biti šifrirana na isti način ukoliko se njihove početne pozicije razlikuju za neki višekratnik od m. Obrnuto, ako uočimo dva identična odsječka u šifratu, duljine barem 3, tada je vrlo vjerojatno da oni odgovaraju identičnim odsječcima otvorenog teksta.
U Kasiskijevom testu u šifratu tražimo parove identičnih odsječaka duljine barem 3, te zabilježimo udaljenosti između njihovih početnih položaja. Ako na takav način dobijemo udaljenosti d1, d2, ... , onda je razumna pretpostavka da m dijeli većinu di-ova.

Druga metoda za određivanje duljine ključa koristi tzv. indeks koincidencije. Taj je pojam uveo 1920. godine William Friedman u knjizi "Indeks koincidencije i njegove primjene u kriptografiji", koja se smatra jednom od najvažnijih publikacija u povijesti kriptologije.
Neka je x = x1x2 ... xn niz od n slova. Indeks koincidencije od x, u oznaci Ic(x), definira se kao vjerojatnost da su dva slučajna elementa iz x jednaka.
Neka su f0, f1, ... , f25 redom (apsolutne) frekvencije od A, B, C, ... , Z u x. Dva elementa iz x možemo odabrati na n(n-1)/2 načina, a za svaki i = 0, 1, ... , 25 postoji fi(fi-1)/2 načina odabira dvaput i-tog slova. Stoga vrijedi formula
Ic(x) = ![]() i
fi(fi-1) /
n(n-1).
i
fi(fi-1) /
n(n-1).
Ic(x) 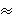
![]() i
pi2
i
pi2 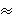 0.064
0.064
Pretpostavimo sada da imamo šifrat y =
y1y2 ...
yn
koji je dobiven Vigenèreovom šifrom. Rastavimo y na
m podnizova z1, z2, ... ,
zm tako da y napišemo,
po stupcima, u matricu dimenzija m
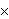 (n/m).
Redci ove matrice su upravo traženi podnizovi
z1, z2, ... ,
zm.
Ako je m jednak duljini ključne riječi, onda su elementi
istog retka matrice šifrirani pomoću istog slova ključa, pa
bi svi
Ic(zi) trebali biti
približno jednaki 0.064. S druge strane, ako m nije duljina
ključne riječi, onda će zi-ovi izgledati
kao više-manje slučajni nizovi slova, budući da su
dobiveni pomacima pomoću različitih
slova ključa. Primijetimo da za potpuno slučajni niz imamo
(n/m).
Redci ove matrice su upravo traženi podnizovi
z1, z2, ... ,
zm.
Ako je m jednak duljini ključne riječi, onda su elementi
istog retka matrice šifrirani pomoću istog slova ključa, pa
bi svi
Ic(zi) trebali biti
približno jednaki 0.064. S druge strane, ako m nije duljina
ključne riječi, onda će zi-ovi izgledati
kao više-manje slučajni nizovi slova, budući da su
dobiveni pomacima pomoću različitih
slova ključa. Primijetimo da za potpuno slučajni niz imamo
Ic 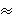 26
. (1/26)2
= 1/26
26
. (1/26)2
= 1/26 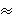 0.038.
0.038.
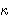
 = 0.064 i
= 0.064 i
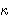
 = 0.038
(p = plaintext = otvoreni tekst, r = random = slučajan)
su dovoljno daleko jedna od druge, tako da ćemo najčešće na
ovaj način moći odrediti točnu duljinu ključne riječi (ili
potvrditi pretpostavku dobivenu pomoću Kasiskijeve metode).
Napomenimo da je u engleskom jeziku
= 0.038
(p = plaintext = otvoreni tekst, r = random = slučajan)
su dovoljno daleko jedna od druge, tako da ćemo najčešće na
ovaj način moći odrediti točnu duljinu ključne riječi (ili
potvrditi pretpostavku dobivenu pomoću Kasiskijeve metode).
Napomenimo da je u engleskom jeziku
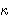
 = 0.065,
u njemačkom 0.076, u francuskom 0.078, u talijanskom 0.074,
u španjolskom 0.078, a u ruskom 0.053.
Odavde zaključujemo da za primjenu ove metode nije nužno
znati na kojem je jeziku pisan otvoreni tekst.
Jedina bitna pretpostavka jest da
se za jezik na kojemu je pisan otvoreni tekst veličina
= 0.065,
u njemačkom 0.076, u francuskom 0.078, u talijanskom 0.074,
u španjolskom 0.078, a u ruskom 0.053.
Odavde zaključujemo da za primjenu ove metode nije nužno
znati na kojem je jeziku pisan otvoreni tekst.
Jedina bitna pretpostavka jest da
se za jezik na kojemu je pisan otvoreni tekst veličina
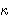
 značajno razlikuje od
0.038.
značajno razlikuje od
0.038.
Primjer 5: Vigenereovom šifrom dobiven je šifrat
GSIQITUKQIEAOHRVUGLTAZGHXUHLPJ
MRTTNQRBZIAVBTGQTBYMYAIVOMZTAI
XJBTEDEWVQWADVWGOOKNQNTCIPEGPY
BOKUSECNWELSBSNUVBTTASMBTOIFHE
ZAEPDQIGAYUCBQSYILYIOOFZTASHIR
ASMKEEESUENAKLQOIMHXUJXGMWOKPK
UNTSRAGMLOETTCIAMTQIBOSLPVNTHP
UNBQINIMU
Primijenimo najprije Kasiskijev test. Uočavamo nekoliko trigrama
koji se dvaput pojavljuju u šifratu. To su
HXU s početkom na pozicijama 24 i 169
(169 - 24 = 145 = 5 . 29),
VBT s početkom na pozicijama 42 i 107
(107 - 42 = 65 = 5 . 13),
ZTA (144 - 57 = 87 =
3 . 29),
TCI (193 - 83 = 110 =
2 . 5 . 11),
TAS (146 - 109 = 35 = 5 . 7) i
ASM (141 - 111 = 40 =
5 . 8).
Odavde se kao najvjerojatnija duljina ključne riječi
nameće broj m = 5, koji dijeli sve osim jedne od razlika
početnih pozicija ponovljenih trigrama.
Pogledajmo hoćemo li pomoću indeksa koincidencije doći do istog zaključka. Za m = 1 je Ic = 0.044; za m = 2 su indeksi 0.048 i 0.042; za m = 3 su 0.049, 0.046 i 0.039; za m = 4 su 0.040, 0.039, 0.047 i 0.042, dok za m = 5 dobivamo indekse 0.061, 0.059, 0.080, 0.053 i 0.074. Sada već s prilično velikom sigurnošću možemo zaključiti da je duljina ključne riječi jednaka 5.
Sljedeće je pitanje kako odrediti ključnu riječ ukoliko znamo njezinu duljinu. Tu nam može pomoći međusobni indeks koincidencije dvaju nizova.
|
Definicija: Neka su x =
x1x2 ... xn i y =
y1y2 ... yn' dva niza od n, odnosno
n' slova. Međusobni indeks koincidencije
od x i y, u oznaci MIc(x,y),
definira se kao vjerojatnost da je slučajni element od x
jednak slučajnom elementu od y. Ako frekvencije od
A, B, C, ... , Z u x i y označimo s
f0, f1, ... ,
f25, odnosno
f'0, f'1, ... ,
f'25, onda je
MIc =
|
Neka je sada m duljina ključne riječi, a neka su podnizovi z1, z2, ... , zm dobiveni kao prije.
Pretpostavimo da je K = (k1, k2, ... , km) ključna riječ i pokušajmo ocijeniti MIc(zi,zj). Promotrimo proizvoljno slovo u zi i proizvoljno slovo u zj. Vjerojatnost da su oba ova slova jednaka A je
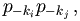
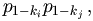
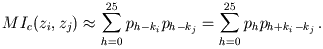
________________________________________________________
relativni pomak očekivana vrijednost od MIc
________________________________________________________
0 0.064
1 0.039
2 0.031
3 0.031
4 0.044
5 0.040
6 0.039
7 0.033
8 0.040
9 0.042
10 0.036
11 0.036
12 0.036
13 0.039
________________________________________________________
Važno je uočiti da ako je pomak jednak 0, onda je ocjena
0.064, a ako je pomak različit od 0, onda su ocjene
između 0.031 i 0.044 - dakle, bitno manje. Ovo zapažanje
može se iskoristiti za određivanje vrijednosti
q = ki - kj.
Pretpostavimo da smo fiksirali zi pa promotrimo efekt šifriranja zj s A, B, C, ... . Tako dobivene nizove označimo sa zj0, zj1, ... . Za g = 0,1,...,25 izračunamo indeks MIc(zi, zjg) po formuli
MIc(x, yg) =
![]() i
fif'i-g /
nn'.
i
fif'i-g /
nn'.
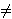 q trebao bi varirati između 0.031 i 0.044.
q trebao bi varirati između 0.031 i 0.044.
Na ovaj način možemo ustvrditi relativne pomake bilo koja dva podniza zi i zj. Nakon što to učinimo, ostaje nam samo 26 mogućih ključnih riječi koje onda možemo ispitati jednu po jednu.
No, malom modifikacijom ove metode, do ključne riječi možemo doći učinkovitije. Umjesto međusobnog indeksa koincidencije nizova zi i zjg, računat ćemo MIc(x, zjg), gdje je x niz koji odgovara tipičnom tekstu na hrvatskom jeziku. To znači da su njegove relativne frekvencije fi / n približno jednake pi, pa je
MIc(x, zjg)
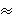
![]() i
pi f'i-g /
n'.
i
pi f'i-g /
n'.
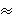 0.064 ako je g =
-kj mod 26, a da je inače
MIc(x, zjg) < 0.045.
0.064 ako je g =
-kj mod 26, a da je inače
MIc(x, zjg) < 0.045.
Prema tome, da bismo odredili j-to slovo kj ključne riječi,
postupamo na sljedeći način. Za
0 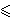 g
g
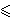 25 izračunamo
25 izračunamo
Mg =
![]() i
pi f'i-g /
n'.
i
pi f'i-g /
n'.
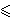 g
g
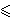 25 }, te stavimo
kj = -h mod 26.
25 }, te stavimo
kj = -h mod 26.
Nastavak primjera 5: Već smo zaključili da je m = 5. Za j = 1,2,3,4,5 izračunajmo vrijednosti M0, M1, ... , M25. Te vrijednosti nalaze se u sljedećoj tablici.
Iz tablice iščitavamo redom:
USPJE HURJE SAVAN JUNEP OZNAT IHSIF ARAMJ ERISE OVIMC ETIRI MAPOK AZATE LJIMA REDOM KAKOS UOVDJ ENAVE DENIU PORNO SCUPA ZSILJ IVIMP OSTUP CIMAA NALIZ EINTU ICIJO MISRE COMSP OSOBN OSTDA SEZNA BAREM CITAT IJEZI KORIG INALN OGTEK STAVE OMAJE POZEL JNAAL INIJE BITNAili, s umetnutim "kvačicama", razmacima i interpunkcijom:
Uspjeh u rješavanju nepoznatih šifara mjeri se ovim četirima pokazateljima, redom kako su ovdje navedeni: upornošću, pažljivim postupcima analize, intuicijom i srećom. Sposobnost da se zna barem čitati jezik originalnog teksta veoma je poželjna, ali nije bitna.
Tako glase prve dvije rečenice Udžbenika za rješavanje vojnih šifara autora Parkera Hitta, jednog od najpoznatijih američkih kriptografa iz vremena Prvog svjetskog rata. Koliko je u njima Hitt bio u pravu, možda može prosuditi i čitatelj ovog članka nakon što pokuša riješiti nagradne zadatke.