Broj 2


















Matko Botinčan, Dubravko Lapaine,
Rudolf Markulin, Ana Žgaljić
Vibracije mehaničkih sustava

Teorija | Primjeri | Download | Linkovi | Dno stranice | Verzija za printanje
Teorija
KRATKA (STVARNO KRATKA) POVIJEST PROUČAVANJA VIBRACIJA
Ljudi su se počeli zanimati za vibracije već od pojave prvih muzičkih instrumenata, vjerojatno bubnjeva i zviždaljki. Iako su već tada opažena stroga pravila, to još ne možemo zvati znanošću. Grčki filozof i matematičar Pitagora (582-507 pr.K.) smatra se prvim koji je na znanstvenoj osnovi promatrao zvukove i glazbu. Poznata su njegova promatranja ovisnosti duljine i napetosti žice i visine tona koji se proizvodi. Od njegovih istraživanja ništa nije ostalo zapisano. Galileo Galilei (1564-1642) smatra se osnivačem moderne eksperimentalne znanosti. Proučavao je jednostavna njihala jedne crkve u Pisi. Jednog dana, jer mu je propovijed bila dosadna, Galileo se zagledao u strop. Njišuća svjetiljka zaokupila je njegovu pažnju i mjerenjima njenih kretanja ustanovio je, na svoje zaprepaštenje, da je period njihanja neovisan o amplitudi kojom se njihalo njiše. Galileo je ostavio dva pisana djela i od tad su se stvari počele znatno brže razvijati. Od poznatih matematičara i fizičara koji su se bavili problemom vibracija tu su još i: Sir Isaac Newton (1642-1727), Brook Taylor (1685-1731), Daniel Bernoulli (1700-1782), Jean D'Alembert (1717-1783), Leonard Euler (1707-1783), Simeon Poisson (1781-1840), G. R. Kirchoff (1842-1887)...pa sve do suvremenih.
VAŽNOST PROUČAVANJA VIBRACIJA
Većina ljudskih aktivnosti uključuje vibracije u jednom od njezinih pojavnih oblika. Primjerice: čujemo jer se vibracije prenose preko naših bubnjića, disanje je povezano s vibracijom naših pluća, hodanje uključuje (periodičke) oscilacije naših ruku i nogu, a govorimo zahvaljujući vibriranju naših glasnica.
Većina vozila ima vibracijskih problema zbog neuravnoteženosti motora. Na primjer, neuravnoteženost diesel motora može proizvesti potresne valove dovoljno jake da budu smetnja u urbanim zonama. Kotači lokomotiva se pri velikim brzinama zbog neuravnoteženosti mogu odvojiti više od centimetra od tračnica. U turbinama vibracije uzrokuju spektakularne mehaničke kvarove. Općenito, vibracije rezultiraju bržim trošenjem i kvarovima dijelova motora kao što su nosači i kotači, a također stvaraju i jaku buku.
Kad god se prirodna frekvencija vibracije motora ili strukture podudara s frekvencijom vanjskog poticaja, nastaje fenomen koji se zove rezonancija. Ona dovodi do iznimnih odstupanja i kvarova. Literatura je puna primjera razornog djelovanja rezonancija (vidi filmić razrušenog mosta tacoma.mpeg). Zbog devastirajućeg efekta kojeg vibracije imaju na strojeve i strukture, testiranje na vibracije postalo je standardan postupak u dizajnu i razvoju većine inženjerskih sustava.
Usprkos svojim štetnim efektima, vibracije se mogu uspješno iskoristiti u nekoliko potrošačkih i industrijskih primjena. Štoviše, primjena vibracijske opreme proteklih se godina znatno povećala. Na primjer, vibracije su iskorištene u vibracijskim tekućim vrpcama, sijačima, sitima, perilicama rublja, električnim četkicama za zube, zubarskim bušilicama, satovima i električnim masažnim uređajima. Vibracije se koriste za simulacije potresa radi geoloških istraživanja i pri istraživanjima dizajna nuklearnih reaktora.
OSNOVNI KONCEPTI VIBRACIJA
Svako gibanje koje se ponavlja u nekom vremenskom intervalu zove se vibracija ili oscilacija. Gibanje njihala je tipičan primjer vibracija.
Vibracije u sustavu uključuju prijenos potencijalne energije u kinetičku i obrnuto. Ako je sustav prigušen, energija se gubi u svakom ciklusu.
Stupnjevi slobode: minimalni broj nezavisnih
koordinata potrebnih da se u potpunosti odredi pozicija svih
dijelova sustava u svakom trenutku vremena definira stupnjeve
slobode. Jednostavno njihalo (kao na slici) predstavlja sustav s
jednim sustavom slobode. Na primjer, gibanje njihala može se
predstaviti u terminima kuta ![]() ili u terminima
Kartezijevih koordinata
ili u terminima
Kartezijevih koordinata ![]() i
i ![]() . Ako se koordinate
. Ako se koordinate ![]() i
i ![]() uzmu za opisivanje gibanja, mora se uočiti da te koordinate
nisu nezavisne. Povezane su, zbog konstante duljine niti
uzmu za opisivanje gibanja, mora se uočiti da te koordinate
nisu nezavisne. Povezane su, zbog konstante duljine niti ![]() ,
relacijom
,
relacijom ![]() . Stoga bilo koja od koordinata
. Stoga bilo koja od koordinata ![]() i
i ![]() može biti odabrana za opisivanje gibanja njihala. Mi ćemo
se ovdje baviti sustavima s jednim stupnjem slobode.
može biti odabrana za opisivanje gibanja njihala. Mi ćemo
se ovdje baviti sustavima s jednim stupnjem slobode.
MATEMATIČKA NADOPUNA (derivacija)
U ovom ćemo poglavlju probati "na prste" objasniti derivacije.
Nećemo zalaziti u stroge matematičke definicije, nego
ćemo im pristupiti tako da steknemo što bolji osjećaj o tome
što su i kako nam derivacije koriste za rješavanje naših
problema. Neka je dana funkcija ![]() , te neka je to realna funkcija
realne varijable (
, te neka je to realna funkcija
realne varijable (
![]() ). Derivacija funkcije
). Derivacija funkcije
![]() u nekoj točki
u nekoj točki
![]() (ova oznaka znači da je
(ova oznaka znači da je ![]() neki
realan broj) definira se kao
neki
realan broj) definira se kao
To zapravo znači da je derivacija funkcije ![]() u točki
u točki ![]() realan broj
realan broj ![]() oko kojega se nakupljaju vrijednosti
oko kojega se nakupljaju vrijednosti
![]() za neki izbor
za neki izbor ![]() -ova koji su "dovoljno"
blizu
-ova koji su "dovoljno"
blizu ![]() . Znači, nakupljaju li se
. Znači, nakupljaju li se ![]() -evi oko
-evi oko ![]() ,
vrijednosti
,
vrijednosti
![]() nakupljat će se oko
nakupljat će se oko
![]() .
.
Sada kada znamo što je to derivacija funkcije ![]() u točki,
možemo vidjeti što je to derivacija funkcije.
u točki,
možemo vidjeti što je to derivacija funkcije.
Derivacija funkcije je funkcija definirana na istoj domeni (![]() )
koja svakoj točki pridružuje derivaciju u točki te
funkcije i označavamo je s
)
koja svakoj točki pridružuje derivaciju u točki te
funkcije i označavamo je s ![]() . Gotovo sve funkcije koje
svakodnevno koristimo su derivabilne (imaju derivaciju) i njihove
su nam derivacije poznate. Za one druge funkcije, koje nemaju
derivaciju (ima i takvih!), kažemo da nisu derivabilne. Za
njih ne vrijedi ono "nakupljanje". Npr.
. Gotovo sve funkcije koje
svakodnevno koristimo su derivabilne (imaju derivaciju) i njihove
su nam derivacije poznate. Za one druge funkcije, koje nemaju
derivaciju (ima i takvih!), kažemo da nisu derivabilne. Za
njih ne vrijedi ono "nakupljanje". Npr. ![]() . Sve derivacije
važnijih funkcija mogu se pronaći u bilo kojim matematičkim tablicama.
. Sve derivacije
važnijih funkcija mogu se pronaći u bilo kojim matematičkim tablicama.
Analogno se definira ![]() tj. druga derivacija funkcije
tj. druga derivacija funkcije ![]() , ili
derivacija funkcije
, ili
derivacija funkcije ![]() , te sve derivacije višeg reda.
, te sve derivacije višeg reda.
Pokušajmo vidjeti što je to derivacija u fizikalnom smislu. Zamislimo da
imamo neko vozilo koje u vremenu ![]() prijeđe put
prijeđe put ![]() . Dakle,
položaj tog vozila u bilo kojem trenutku dan je nekom
funkcijom ovisnom o
. Dakle,
položaj tog vozila u bilo kojem trenutku dan je nekom
funkcijom ovisnom o ![]() . Recimo za
. Recimo za ![]() vozilo će prijeći
put
vozilo će prijeći
put ![]() Npr. ako se radi o jednolikom gibanju, funkcija
Npr. ako se radi o jednolikom gibanju, funkcija ![]() bila bi oblika
bila bi oblika
gdje je ![]() neki realan broj.
neki realan broj.
(Kako znamo da ona izgleda baš tako? Jednoliko gibanje je ono
gibanje kod kojega je u jednakim vremenskim razmacima prijeđen
jednak put, tj. funkcija ![]() mora zadovoljavati
mora zadovoljavati
![]() za
za ![]() , a to očito zadovoljavaju
funkcije oblika (1) i samo takve funkcije).
, a to očito zadovoljavaju
funkcije oblika (1) i samo takve funkcije).
Za jednoliko gibanje derivacija bi bila
ali mi znamo da je kod jednolikog gibanja brzina konstantna i da
je ona u nekom trenutku ![]() , nakon prijeđenog puta
, nakon prijeđenog puta ![]() ,
baš jednaka
,
baš jednaka
![]() , pa je, dakle, derivacija
ovakve funkcije
, pa je, dakle, derivacija
ovakve funkcije ![]() baš brzina, tj. derivacija funkcije
baš brzina, tj. derivacija funkcije ![]() u
trenutku (točki)
u
trenutku (točki) ![]() je baš brzina u trenutku (točki
je baš brzina u trenutku (točki ![]() ).
Na ovom primjeru vidjeli smo fizikalno značenje derivacije.
Dakle, derivacija je zapravo brzina. Analogno se može pokazati
da je akceleracija druga derivacija, tj. ako je gibanje tijela
dano nekom funkcijom
).
Na ovom primjeru vidjeli smo fizikalno značenje derivacije.
Dakle, derivacija je zapravo brzina. Analogno se može pokazati
da je akceleracija druga derivacija, tj. ako je gibanje tijela
dano nekom funkcijom ![]() , akceleracija tog tijela bit će
, akceleracija tog tijela bit će
![]() .
.
Diferencijalnom jednadžbom zvat ćemo onu jednadžbu u
kojoj se pojavljuje derivacija neke funkcije, odnosno nešto
ovakvog oblika:
To bi bila diferencijalna jednadžba prvog reda zato jer se
funkcija ![]() pojavljuje s najviše prvom derivacijom.
O tome kakva je funkcija
pojavljuje s najviše prvom derivacijom.
O tome kakva je funkcija ![]() nećemo se previše brinuti.
Recimo samo da će sve funkcije
nećemo se previše brinuti.
Recimo samo da će sve funkcije ![]() koje će se nama
pojaviti biti "dobre".
koje će se nama
pojaviti biti "dobre".
Rješenjem takve diferencijalne jednadžbe, nazovimo ga
![]() , zvat ćemo funkciju koja zadovoljava (2), tj. da
uvrštavanjem
, zvat ćemo funkciju koja zadovoljava (2), tj. da
uvrštavanjem ![]() u (2) zaista dobijemo jednakost.
u (2) zaista dobijemo jednakost.
Sada kad "znamo" što je derivacija, pokušajmo
predočiti što je integral. Integral, označavamo ga s
![]() , bila bi "obrnuta derivacija", odnosno integral funkcije
, bila bi "obrnuta derivacija", odnosno integral funkcije
![]() bila bi sama funkcija
bila bi sama funkcija ![]() . Npr.
. Npr.
![]() .
.
MATEMATIČKO NJIHALO
Zamislimo matematičko njihalo kao kuglicu mase ![]() obješenu o nit duljine
obješenu o nit duljine ![]() . Nit je "idealna", tj. smatramo da
je nerastezljiva i da nema masu. Kuglicu ne promatramo u
klasičnom smislu, nego kao masu koncentriranu u jednoj
točki. Ako kuglicu pomaknemo iz položaja ravnoteže i
pustimo, ona se zanjiše i njezino gibanje dano je
jednadžbom
. Nit je "idealna", tj. smatramo da
je nerastezljiva i da nema masu. Kuglicu ne promatramo u
klasičnom smislu, nego kao masu koncentriranu u jednoj
točki. Ako kuglicu pomaknemo iz položaja ravnoteže i
pustimo, ona se zanjiše i njezino gibanje dano je
jednadžbom
gdje je ![]() kao na slici.
Znamo da je za
kao na slici.
Znamo da je za ![]() dovoljno mali
dovoljno mali
![]() pa u slučaju ako promatramo titranje njihala oko položaja
ravnoteže, dobivamo jednadžbu gibanja za male oscilacije:
pa u slučaju ako promatramo titranje njihala oko položaja
ravnoteže, dobivamo jednadžbu gibanja za male oscilacije:
OPRUGA
Opruga je tijelo napravljeno od žice savijene u helikoidu
(krivulja koja opisuje izgled opruge). Zamišljamo da je broj
navoja velik i da je ona izdužena, tj. da je poprečni
presjek malen u odnosu na duljinu. Sila opruge ima smjer prema
nutrini opruge i iznosa je
Konstanta opruge ![]() ovisi o materijalu opruge, radijusu namotaja
ovisi o materijalu opruge, radijusu namotaja
![]() , broju namotaja
, broju namotaja ![]() i radijusu žice
i radijusu žice ![]() . Točnije,
. Točnije, ![]() je
dan izrazom
je
dan izrazom
![]() , gdje je
, gdje je ![]() karakteristika materijala opruge. Pogledajmo kako se ponašaju dvije opruge
spojene serijski odnosno paralelno. U oba slučaja
želimo zamijeniti dvije opruge jednom tako da za danu
oprugu odaberemo dobar
karakteristika materijala opruge. Pogledajmo kako se ponašaju dvije opruge
spojene serijski odnosno paralelno. U oba slučaja
želimo zamijeniti dvije opruge jednom tako da za danu
oprugu odaberemo dobar ![]() . Neka je
. Neka je ![]() konstanta prve opruge,
a
konstanta prve opruge,
a ![]() konstanta druge opruge.
konstanta druge opruge.
U slučaju serijskog spoja imamo:
- opruga1 produlji se za
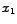 ,
,
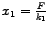 ,
,
- opruga2 produlji se za
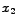 ,
,
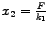 .
.
Zamijenimo ih jednom oprugom koja se produlji za ![]() , pa sada imamo
, pa sada imamo
tj.
Serijski spojene opruge ponašaju se kao paralelno spojeni otpornici.
Za slučaj paralelnog spoja opruga, na sličan način
dobijemo da je ![]() opruge koja bi zamijenila dvije paralelno
spojene opruge jednak zbroju njihovih konstanti, tj.
opruge koja bi zamijenila dvije paralelno
spojene opruge jednak zbroju njihovih konstanti, tj.
ELASTIČNI ŠTAP
Pretpostavimo da imamo homogeni elastični štap (npr. velika
gumica za brisanje). Neka štap u blizini hvatišta uvijek
ostaje okomit na ravninu hvatišta. Na kraj štapa stavimo masu
![]() ili djelujemo silom
ili djelujemo silom ![]() . Neka je
. Neka je ![]() funkcija koja opisuje pomak
u tom smjeru, tj. funkcija koja opisuje transverzalni pomak.
Jednadžba ravnoteže za ovaj štap dana je kao
funkcija koja opisuje pomak
u tom smjeru, tj. funkcija koja opisuje transverzalni pomak.
Jednadžba ravnoteže za ovaj štap dana je kao
gdje je ![]() Youngov modul elastičnosti,
Youngov modul elastičnosti, ![]() moment inercije
presjeka štapa,
moment inercije
presjeka štapa, ![]() linijska gustoća sile. Za ovakav štap se
pokaze da vrijedi
linijska gustoća sile. Za ovakav štap se
pokaze da vrijedi
Nadalje, uzimamo da je
(![]() je moment uvijanja štapa), što se dobije integracijom prethodne
jednadžbe. Uzmemo li da je
je moment uvijanja štapa), što se dobije integracijom prethodne
jednadžbe. Uzmemo li da je ![]() (tj. štap nema mase) i
(tj. štap nema mase) i ![]() integracijom glavne jednadžbe dobivamo
integracijom glavne jednadžbe dobivamo
tj. ovime smo opet dobili jednadžbu za silu opruge, s time da je koeficijent opruge zamijenjen izrazom koji ovisi o svojstvima štapa.
Na sličan način, kad bismo promatrali longitudinalni pomak
štapa dobili bismo izraz
gdje je ![]() površina presjeka, pa i u slučaju ovakvog
gibanja, štap djeluje kao opruga.
površina presjeka, pa i u slučaju ovakvog
gibanja, štap djeluje kao opruga.
SLOBODNE VIBRACIJE
Zamislimo masu ![]() obješenu na oprugu konstante
obješenu na oprugu konstante ![]() .
Jednadžba gibanja mase
.
Jednadžba gibanja mase ![]() dana je prema drugom Newtonovom
zakonu kao
dana je prema drugom Newtonovom
zakonu kao
Znamo da je akceleracija derivacija brzine pa je ona dana kao
Stoga se jednadžba svodi na
Do iste jednadžbe dolazimo i primjenom zakona očuvanja energije.
Jednadžbu ![]() rješavamo po
rješavamo po ![]() i na taj način
dobivamo funkciju
i na taj način
dobivamo funkciju ![]() koja opisuje gibanje mase obješene na
oprugu. Jednadžba se zapisuje u obliku
koja opisuje gibanje mase obješene na
oprugu. Jednadžba se zapisuje u obliku
Opće rješenje ove jednadžbe dano je u obliku
Period ovog gibanja je
![]() .
. ![]() ovisi samo o
masi i konstanti opruge. Ako imamo zadan početni položaj
mase
ovisi samo o
masi i konstanti opruge. Ako imamo zadan početni položaj
mase ![]() i početnu brzinu
i početnu brzinu ![]() lako se
izračunaju konstante
lako se
izračunaju konstante ![]() i
i ![]() . Uvrštavanjem
. Uvrštavanjem ![]() u (3)
dobivamo
u (3)
dobivamo ![]() . Ako deriviramo (3), te nakon toga
uvrstimo
. Ako deriviramo (3), te nakon toga
uvrstimo ![]() u dobivenu jednadžbu, dobivamo
u dobivenu jednadžbu, dobivamo
![]() . Na taj način dobivamo rješenje u
obliku
. Na taj način dobivamo rješenje u
obliku
Primjedba. Ako za ![]() i
i ![]() uzmemo da je
uzmemo da je
![]() i
i
![]() , za neke
, za neke ![]() i
i ![]() dobivamo da je
dobivamo da je
![]() i
i
![]() . U tom slučaju
rješenje možemo zapisati u obliku
. U tom slučaju
rješenje možemo zapisati u obliku
Npr. graf jednog takvog rješenja izgleda ovako:
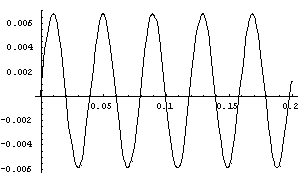
SLOBODNE VIBRACIJE S VISKOZNIM PRIGUŠENJEM
Jednadžba ovakvog sustava dana je kao
![]() ovisi o konstanti
ovisi o konstanti ![]() prigušivača i
o brzini, tj. dana je izrazom
prigušivača i
o brzini, tj. dana je izrazom ![]() . Na taj način dobivamo
jednadžbu
. Na taj način dobivamo
jednadžbu
Da bi riješili ovu jednadžbu rješavamo pripadnu
karakterističnu jednadžbu
![]() .
Dobivamo rješenja
.
Dobivamo rješenja
Opće rješenje jednadžbe (4) tada je dano kao
Razlikujemo tri vrste rješenja:
- 1. Slučaj.
Vrijedi
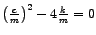 tj.
tj.
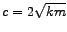 . S ovakvom konstantom prigušenja
. S ovakvom konstantom prigušenja 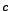 dobivamo
KRITIČNO gušenje. U tom je slučaju rješenje dano
izrazom
dobivamo
KRITIČNO gušenje. U tom je slučaju rješenje dano
izrazom
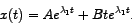
Graf jednog ovakvog rješenja:
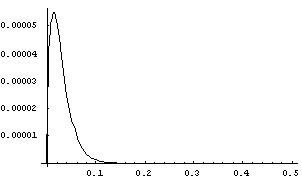
- 2. Slučaj.
Vrijedi
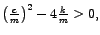 tj.
tj.
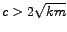 . U ovom slučaju viskozno prigušenje veće je
od kritičnog. Rješenje je dano u obliku
(5), ali zbog ovakvog
. U ovom slučaju viskozno prigušenje veće je
od kritičnog. Rješenje je dano u obliku
(5), ali zbog ovakvog 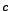 ovo rješenje ponovno trne.
Ovakav slučaj zovemo VELIKO prigušenje.
ovo rješenje ponovno trne.
Ovakav slučaj zovemo VELIKO prigušenje.
Graf jednog ovakvog rješenja:
- 3. Slučaj.
Vrijedi
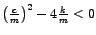 , tj.
, tj.
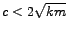 . U ovom slučaju viskozno prigušenje
manje je od kritičnog. Kako dobivamo kompleksna rješenja karakteristične jednadžbe,
rješenje polazne jednadžbe dano je u obliku
. U ovom slučaju viskozno prigušenje
manje je od kritičnog. Kako dobivamo kompleksna rješenja karakteristične jednadžbe,
rješenje polazne jednadžbe dano je u obliku
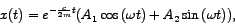
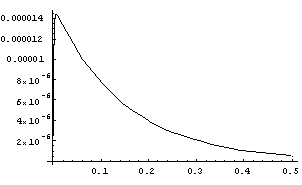
gdje je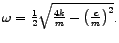 Ako uvedemo zamjenu
Ako uvedemo zamjenu
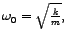 dobivamo
dobivamo
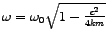 . Uočimo da
je u ovom slučaju
. Uočimo da
je u ovom slučaju
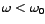 . Ovakav slučaj zovemo
MALO prigušenje.
. Ovakav slučaj zovemo
MALO prigušenje.
Graf jednog ovakvog rješenja:
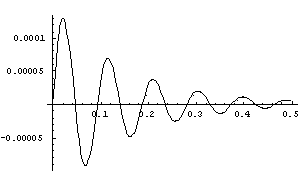
PRISILNE VIBRACIJE
Prisilne vibracije zbivaju se kada npr. na masu ![]() koja se nalazi
obješena na opruzi konstante
koja se nalazi
obješena na opruzi konstante ![]() još djelujemo nekom
silom
još djelujemo nekom
silom ![]() . U tom slučaju jednadžba za masu
. U tom slučaju jednadžba za masu ![]() koja izlazi
iz 2. Newtonovog zakona glasi
koja izlazi
iz 2. Newtonovog zakona glasi
Uzimamo da je
![]() . Sada rješenje
jednadžbe (6) tražimo u obliku
. Sada rješenje
jednadžbe (6) tražimo u obliku
![]() gdje je
gdje je
![]() (pri čemu je
(pri čemu je
![]() kružna frekvencija slobodnih
oscilacija) rješenje homogene jednadžbe
kružna frekvencija slobodnih
oscilacija) rješenje homogene jednadžbe
![]() .
.
Partikularno rješenje tražimo u obliku
![]() .
Uvrštavanjem u (6) dobije se da je
.
Uvrštavanjem u (6) dobije se da je
Tu nastupa problem za
![]() . Taj slučaj razmotrit
ćemo posebno.
. Taj slučaj razmotrit
ćemo posebno.
Dakle, opće rješenje problema (6) dano je kao
Tu imamo superpoziciju dviju harmonijskih vibracija.
Za slučaj
![]() partikularno rješenje
tražimo u obliku
partikularno rješenje
tražimo u obliku
![]() .
Uvrštavanjem u jednadžbu dobijemo da je
.
Uvrštavanjem u jednadžbu dobijemo da je
![]() . Dakle,
u tom slučaju opće je rješenje oblika
. Dakle,
u tom slučaju opće je rješenje oblika
Ovo rješenje u vremenu eksplodira, tj. amplituda sve više raste.
Graf jednog ovakvog rješenja:
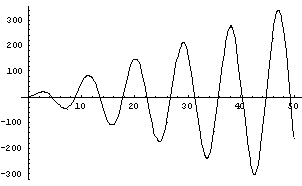
SUSTAVI S VIŠE STUPNJEVA SLOBODE
Sustavi s više stupnjeva slobode su oni sustavi koji zahtjevaju
dvije, tri ili više koordinata da bi ih se u potpunosti moglo opisati.
Jedan od najjednostavnijih primjera sustava s dva stupnja slobode može se vidjeti
na jednoj od idućih animacija. Prikazane su dvije mase
pričvršćene oprugama za zid, čije ponašanje
opisuju dvije linearne koordinate ![]() i
i ![]() .
.
Kao dobar primjer sustava s tri stupnja slobode mogli bismo
uzeti sustav koji se sastoji od tri kuglice
povezane nitima i predstavlja tek nešto kompliciraniju verziju
matematičkog njihala (taj primjer također se može vidjeti na jednoj
od idućih animacija). U tom slučaju položaje kuglica očito možemo
odrediti koordinatama
![]() . No, odmah se može uočiti
da nisu potrebne obje od koordinata
. No, odmah se može uočiti
da nisu potrebne obje od koordinata ![]() , budući su one povezane
relacijom
, budući su one povezane
relacijom
![]() . Umjesto koordinata koje određuju položaj kuglica,
mogli bismo koristiti i samo iznose kuteva
. Umjesto koordinata koje određuju položaj kuglica,
mogli bismo koristiti i samo iznose kuteva ![]() jer su duljine niti u
sustavu konstantne, te je pomoću kutova položaj kuglice u potpunosti
određen. Bilo da koristimo kuteve ili pak neke od
jer su duljine niti u
sustavu konstantne, te je pomoću kutova položaj kuglice u potpunosti
određen. Bilo da koristimo kuteve ili pak neke od ![]() koordinata,
uvijek će nam biti potrebno samo tri (a ne šest) da u potpunosti opišemo
ponašanje sustava.
koordinata,
uvijek će nam biti potrebno samo tri (a ne šest) da u potpunosti opišemo
ponašanje sustava.
Koordinate koje koristimo za opisivanje sustava zovemo
generalizirane koordinate i najčešće ih označavamo s ![]() .
Kao što smo upravo vidjeli, to mogu biti Kartezijeve i
nekartezijeve koordinate.
.
Kao što smo upravo vidjeli, to mogu biti Kartezijeve i
nekartezijeve koordinate.
Često se, da bi se jasnije mogle uočiti pojedine bitne karakteristike oscilacija sustava s više stupnjeva slobode, cjelokupno ponašanje sustava razlaže na njegove osnovne komponente. Te osnovne komponente predstavljaju one najbitnije elemente gibanja sustava i nazivaju se osnovni modovi ponašanja (gibanja). Ponašanje čitavog sustava tada se može prikazati kao superpozicija (linearna kombinacija) njegovih osnovnih modova. Kako je postupak nalaženja osnovnih modova ponešto kompliciraniji, ovdje se nećemo upuštati u njegovo matematičko opisivanje, ali na slijedećim animacijama vizualno će se moći uočiti o čemu je tu otprilike riječ.
Primjeri
Vibracije s jednim stupnjem slobode:
|
Download
|
Cjelokupni tekst u PDF formatu: vibracije.pdf Tacoma Bridge - MPEG film (kraća verzija): tacoma.mpeg |
Linkovi
|
Tacoma Bridge - AVI film (duža verzija): http://www.cse.polyu.edu.hk/~ctbridge/goodies/ Tacoma Bridge - još neki filmovi: http://didaktik.physik.uni-wuerzburg.de/~pkrahmer/home/galileo.html |
Vrh stranice | Teorija | Primjeri | Download | Linkovi | Verzija za printanje