
Hrvatski matematički elektronski časopis math.e

|
Hrvatski matematički elektronski časopis math.e |
| http://www.math.hr/~mathe/ |
Teorija igara - matematičko modeliranje konfliktnih situacija
Vedran Krčadinac
Teorija igara je matematička disciplina koja se razvila sredinom 20. stoljeća. Početkom se može smatrati knjiga Theory of games and economic behavior (Teorija igara i ekonomsko ponašanje) matematičara Johna von Neumanna i ekonomista Oskara Morgensterna [3]. Još jedan od fundamentalnih doprinosa je rad Johna Nasha [2], za koji mu je kasnije dodijeljena Nobelova nagrada za ekonomiju (Nobelova nagrada ne dodjeljuje se za matematiku). O Johnu Nashu nedavno je snimljen biografski film Genijalni um. U početku je glavna motivacija za razvoj bila ekonomska, ali je teorija igara našla primjene i u drugim društvenim znanostima, vojne primjene, pa čak i primjene u biologiji. Zanimljivi primjeri iz biologije mogu se naći u knjizi Richarda Dawkinsa Sebični gen [1].
Pojednostavljeno rečeno, teorija igara bavi se situacijama konflikta između dvaju ili više sudionika. Cilj je odrediti ponašanje sudionika koje je za njih najpovoljnije, pod pretpostavkom da su racionalni. Konflikt je reguliran strogo definiranim pravilima kao u društvenim igrama poput pokera, monopola, "čovječe ne ljuti se" i sličnim. Teorija igara omogućuje preciznu analizu takvih igara, po čemu je dobila ime. Konflikti u stvarnom životu obično nisu podložni jednostavnim pravilima. Zbog toga je teorija igara uglavnom ostala u okvirima akademskih primjera, a u praksi se dosta rijetko koristi. Ipak, radi se o lijepoj teoriji koja povezuje nekoliko grana matematike i dala je važne doprinose razumijevanju ponašanja u ekonomiji, sociologiji, psihologiji i teoriji evolucije.
Osnovne pojmove teorije igara objasnit ćemo u slučaju igre za dva igrača sume nula. Riječ igra odnosi se na bilo kakav konflikt dviju suprostavljenih strana koji želimo analizirati. To ne mora biti društvena igra, niti sudionici moraju biti osobe, usprkos tome što ih nazivamo igračima. Ograničenje na igre sume nula znači da je gubitak prvog igrača jednak dobitku drugog, i obrnuto. Taj dobitak/gubitak treba biti izražen numerički, što nije uvijek jednostavno u realnim situacijama. Još jedno ograničenje koje namećemo jest da igrači imaju konačno mnogo strategija, tj. mogućnosti za ponašanje u sukobu.
Promotrimo jednostavan primjer, igru "par - nepar". Igrači istovremeno pokazuju šaku s nekoliko ispruženih prstiju. Ako je zbroj ispruženih prstiju paran, pobjeđuje prvi igrač ("par"); u suprotnom pobjeđuje drugi igrač ("nepar"). Igrači zapravo imaju samo dvije bitno različite mogućnosti: pokazati paran broj prstiju ili pokazati neparan broj prstiju. Za prvog i za drugog igrača potpuno je svejedno hoće li pokazati jedan, tri ili svih pet prstiju. Zato u ovoj igri svaki igrač ima dvije strategije (točnije bi bilo reći čiste strategije, što ćemo uskoro objasniti). Igrač koji je pobijedio dobiva određenu količinu novca od igrača koji je izgubio, recimo jednu kunu. Radi se o igri sume nula jer je iznos koji osvaja pobjednik jednak iznosu koji njegov protivnik gubi. U nekim igrama to nije slučaj, na primjer dio novca može zadržati organizator igre (kockarnica).
Sa stanovišta prvog igrača svi mogući ishodi igre par - nepar su:
| Drugi igrač ("nepar") | |||||||
| Paran broj | Neparan broj | ||||||
| Prvi igrač ("par") | Paran broj |
| |||||
| Neparan broj | |||||||
 n matricom:
n matricom:
|
Važna pretpostavka koju do sada nismo spomenuli je da se igra ponavlja. Ako se par - nepar igra samo jednom, nema smisla govoriti o optimalnom ponašanju igrača. U slučaju kad se igra ponavlja, igrači mogu igrati dobro ili loše i daljnja analiza ima smisla. Pretpostavimo da prvi igrač uvijek pokazuje paran broj prstiju. Njegov će protivnik brzo shvatiti da pokazivanjem neparnog broja uvijek pobjeđuje. Zapravo, ako prvi igrač samo malo češće pokazuje parne nego neparne brojeve, drugi igrač može uvijek pokazivati neparne brojeve i pobjeđivat će češće. Zaključujemo da prvi igrač treba jednakom frekvencijom birati parne i neparne brojeve, a isto naravno vrijedi i za drugog igrača.
Pretpostavimo sada da prvi igrač pokazuje redom paran broj, zatim neparan, pa paran, pa neparan i tako dalje. Čim drugi igrač uoči pravilnost, pokazivat će brojeve suprotne parnosti i uvijek pobjeđivati. Prema tome, igrači ne smiju dozvoliti da protivnik uoči pravilnost u njihovom nizu brojeva. Najbolje im je parnost brojeva birati na slučajan način, bacanjem novčića ili slično. Tako dolazimo do pojma miješane strategije. Radi se o vjerojatnostima prema kojima igrači biraju retke, odnosno stupce matrice isplata. Uobičajeno je za prvog igrača vjerojatnosti zapisivati u vektor-redak P, a za drugog u vektor-stupac Q. Optimalne miješane strategije u igri par - nepar su, dakle,
|
|
 Brojevi pi , qj su
vjerojatnosti, tj. ne smiju biti negativni ni veći od jedan. Osim
toga mora vrijediti
p1+ ... + pm =
q1+ ... + qn = 1
jer igrači u svakom ponavljanju igre biraju točno jednu čistu strategiju.
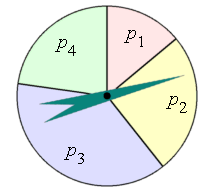
Izbor se, na primjer, može realizirati "kolom sreće" prikazanim na slici.
Brojevi pi , qj su
vjerojatnosti, tj. ne smiju biti negativni ni veći od jedan. Osim
toga mora vrijediti
p1+ ... + pm =
q1+ ... + qn = 1
jer igrači u svakom ponavljanju igre biraju točno jednu čistu strategiju.
Izbor se, na primjer, može realizirati "kolom sreće" prikazanim na slici.
Miješane strategije zapisuju se na opisan način da bismo mogli
množiti matrice P, A i Q. Produkt
P 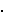 A
A 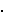 Q jednak je matematičkom
očekivanju dobitka prvog igrača i označava se E(P, Q).
Radi se o broju koji mjeri prosječan dobitak prvog igrača. Prvom igraču
je u interesu da broj bude što veći, a drugom da bude što manji. Igrači
utječu na njega izborom svojih miješanih strategija (prvi igrač
bira P, a drugi Q).
Q jednak je matematičkom
očekivanju dobitka prvog igrača i označava se E(P, Q).
Radi se o broju koji mjeri prosječan dobitak prvog igrača. Prvom igraču
je u interesu da broj bude što veći, a drugom da bude što manji. Igrači
utječu na njega izborom svojih miješanih strategija (prvi igrač
bira P, a drugi Q).
Za igru par - nepar već smo našli optimalne strategije. Vrijednost igre je očekivani dobitak kad oba igrača igraju optimalno, u našem slučaju
|
=  1/2 1/2 1/2 1/2 
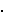 |
  
|
|
  
|
= 0. |
U igri par - nepar vrlo je lako odrediti optimalne strategije i vrijednost igre, jer je igra potpuno simetrična. To nije uvijek tako, čak ni za igre u kojima igrači imaju samo dvije čiste strategije. Na primjer, promotrimo modifikaciju igre par - nepar sa sljedećom matricom isplata:
|
Dvije konkurentske međunarodne tvrtke žele otvoriti predstavništvo u Hrvatskoj. Predstavništvo mogu otvoriti u Osijeku, Rijeci, Splitu ili Zagrebu. Ako otvore predstavništva u istom gradu, podijelit će tržište popola. Za ostale slučaje provedeno je istraživanje i rezultat je prikazan u tablici.
| Druga tvrtka | |||||||||||||||||||||
| Os | Ri | St | Zg | ||||||||||||||||||
| Prva tvrtka | Os |
| |||||||||||||||||||
| Ri | |||||||||||||||||||||
| St | |||||||||||||||||||||
| Zg | |||||||||||||||||||||
Naveden je udio tržišta koji osvaja prva tvrtka ako otvori predstavništvo u gradu koji označava redak, a druga tvrtka u gradu koji označava stupac matrice. Na primjer, ako prva tvrtka otvori predstavništvo u Splitu, a druga u Rijeci, prva tvrtka osvaja 55% tržišta, a druga preostalih 45%. Pretpostavljamo da druga tvrtka uvijek osvaja cijeli preostali dio tržišta, tj. da imamo igru sume nula. To ima ekonomskog smisla ako se radi o djelatnosti koja do sada nije bila zastupljena u Hrvatskoj, pa će tvrtke među sobom podijeliti cijelo tržište. Pobjednikom smatramo tvrtku koja osvoji više od pola tržišta.
U prvoj tvrtki razmišljaju na sljedeći način. Za svaki od četiri svoja izbora traže protivnikov izbor koji je za njih najnepovoljniji. Drugim riječima, traže minimalne brojeve u recima matrice isplata:
| Druga tvrtka | |||||||||||||||||||||
| Os | Ri | St | Zg | ||||||||||||||||||
| Prva tvrtka | Os |
| |||||||||||||||||||
| Ri | |||||||||||||||||||||
| St | |||||||||||||||||||||
| Zg | |||||||||||||||||||||
Od četiriju brojeva obojanih plavo najveći je 50%. Prema tome, prva tvrtka osvaja barem pola tržišta ako otvori predstavništvo u Zagrebu. Za ostale izbore njihov je garantirani dobitak manji, iako maksimalni dobitak može biti veći. Najpovoljniji slučaj za prvu tvrtku bio bi da otvore predstavništvo u Splitu, a njihovi protivnici u Osijeku (tada osvajaju 80% tržišta). Međutim, druga tvrtka također se ponaša racionalno i neće izabrati za sebe nepovoljnu mogućnost (Osijek).
U drugoj tvrtki razmišljaju analogno. Za svaki svoj izbor nalaze najgoru mogućnost za sebe, a među njima onu koja je najpovoljnija. Drugim riječima, traže maksimume stupaca i biraju najmanji od tih maksimuma:
| Druga tvrtka | |||||||||||||||||||||
| Os | Ri | St | Zg | ||||||||||||||||||
| Prva tvrtka | Os |
| |||||||||||||||||||
| Ri | |||||||||||||||||||||
| St | |||||||||||||||||||||
| Zg | |||||||||||||||||||||
Ljubičasto obojani broj označile su obje tvrtke. Za jednu i za drugu najbolje je predstavništvo otvoriti u Zagrebu, jer tada sigurno osvajaju 50% tržišta. To je vrijednost ove igre, a optimalne strategije mogu se matrično zapisati kao
|
| Sedlasta točka je element matrice koji je ujedno minimum retka i maksimum stupca u kojem se nalazi. Igra kojoj matrica isplata sadrži sedlastu točku naziva se strogo određenom. |
Optimalne strategije strogo određene igre imaju jedinicu na mjestu koje odgovara retku, odnosno stupcu u kojem je sedlasta točka, a na svim ostalim mjestima nule. Vrijednost igre je broj upisan u sedlastu točku. Za strogo određene igre lako je naći optimalne strategije i vrijednost igre, ali nisu sve igre takve. Na primjer, modificirana igra par - nepar nema sedlastu točku:
|
Dućan za ekstremne sportove nabavlja snowboarde i bicikle za iduću sezonu. Ako iduće zime padne mnogo snijega, zaradit će prosječno 500 kuna po naručenom snowboardu i 100 kuna po naručenom biciklu. Ako ne padne snijeg, prosječno će izgubiti 100 kuna po naručenom snowboardu i zaraditi 400 kuna po naručenom biciklu. U kojem omjeru trebaju naručiti robu tako da garantirana zarada bude što veća, bez obzira na vremenske prilike?
Ovaj problem također možemo modelirati kao igru sume nula za dva igrača. Prvi igrač je dućan, a drugi priroda. Jasno, priroda nije svjestan igrač koji nastoji smanjiti zaradu dućana, ali sjetimo se da dućan želi maksimizirati garantiranu zaradu. Vlasnik dućana vjeruje u Murphyjev zakon prema kojem će vremenske prilike biti upravo onakve kakve njemu najmanje odgovaraju.
Miješane strategije u ovom primjeru interpretiramo drugačije.
Strategija prvog igrača
P =  p1 p2
p1 p2  određuje udio naručenih snowboarda (p1)
i bicikla (p2). Strategija drugog igrača, Q,
određuje intenzitet kojim će padati snijeg. Prva komponenta (q1)
odgovara zimi bez snijega, a druga komponenta (q2)
zimi s iznimno mnogo snijega. Uz ovakav dogovor matrica isplata glasi:
određuje udio naručenih snowboarda (p1)
i bicikla (p2). Strategija drugog igrača, Q,
određuje intenzitet kojim će padati snijeg. Prva komponenta (q1)
odgovara zimi bez snijega, a druga komponenta (q2)
zimi s iznimno mnogo snijega. Uz ovakav dogovor matrica isplata glasi:
| Priroda | |||||||
| nema snijega | ima snijega | ||||||
| Dućan | snowboardi |
| |||||
| bicikli | |||||||
|
Teorem (von Neumann). Za svaku igru sume nula za dva igrača
postoji par strategija P0, Q0
i broj v sa svojstvima:
|
Zbog ovog teorema pojmovi optimalnih strategija i vrijednosti igre imaju smisla za sve igre, a ne samo za strogo određene. Racionalni igrači izabrat će strategije P0, Q0 i tada će očekivani dobitak prvog igrača biti jednak vrijednosti igre v. Ako prvi igrač izabere strategiju koja nije optimalna, njegov očekivani dobitak može biti veći od v za pojedine strategije drugog igrača, ali postoji strategija Q za koju je očekivani dobitak manji od v. Analogno, ako drugi igrač izabere strategiju koja nije optimalna, prvi igrač ima strategiju P za koju je očekivani dobitak veći od v.
Von Neumannov teorem može se dokazati svođenjem na problem linearnog programiranja.
Taj dokaz je jednostavniji od von Neumannovog originalnog dokaza i daje nam
postupak za nalaženje optimalnih strategija i vrijednosti igre.
Linearno programiranje bavi se minimizacijom i maksimizacijom linearnih
funkcija više varijabli uz uvjete zadane linearnim nejednakostima. Postoji više
efikasnih algoritama za rješavanje takvih problema, među kojima je najpopularniji
simpleks algoritam. Pokazuje se da je za igru s matricom isplata A =
 aij
aij  nalaženje optimalne strategije prvog
igrača P0 =
nalaženje optimalne strategije prvog
igrača P0 =
 p1 p2 ... pm
p1 p2 ... pm  ekvivalentno problemu linearnog programiranja
ekvivalentno problemu linearnog programiranja
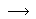 max
max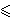 a1j p1 + .. +
amj pm,
j = 1,.., n
a1j p1 + .. +
amj pm,
j = 1,.., n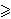 0,
i = 1,.., m
0,
i = 1,.., m
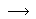 min
min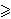 ai1 q1 + .. +
ain qn,
i = 1,.., m
ai1 q1 + .. +
ain qn,
i = 1,.., m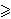 0,
j = 1,.., n
0,
j = 1,.., n
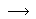 max maxv 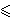 -100 p1 + 400 p2
-100 p1 + 400 p2v 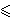 500 p1 + 100 p2
500 p1 + 100 p2p1 + p2 = 1 p1 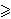 0,
p2 0,
p2 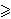 0 0
|
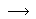 min minu 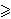 -100 q1 + 500 q2
-100 q1 + 500 q2u 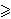 400 q1 + 100 q2
400 q1 + 100 q2q1 + q2 = 1 q1 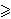 0,
q2 0,
q2 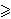 0 0
|
Prikaz metoda za rješavanje problema linearnog programiranja prelazi okvire ovog članka. Probleme ćemo riješiti pomoću programa Mathematica, koji ima efikasne naredbe za optimizaciju Maximize i Minimize. Dovoljno je prepisati funkciju cilja i uvjete u Mathematica notaciji.
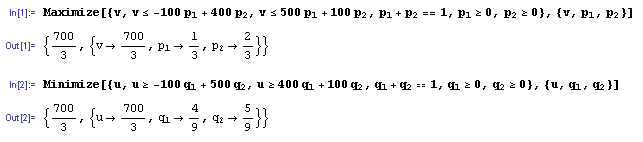
Vidimo da je vrijednost igre v = u = 700/3, a optimalne strategije su
|
Postoje formule za optimalne strategije i vrijednost igre u kojoj igrači imaju samo dvije čiste strategije.
Neka je
|
Uvrštavanjem u formule vidimo da je vrijednost modificirane igre par - nepar v = -1/8, a optimalne strategije su
|
Na kraju članka analizirat ćemo igru koju je autor naučio na odsluženju vojnog roka pod imenom "giapponese". Igraju dva igrača, a kao pribor svaki ima tri novčića. Igrači iza leđa zatvore određen broj novčića u šaku (nula, jedan, dva ili tri) i pokažu zatvorenu šaku protivniku. Cilj je pogoditi zbroj novčića u obje šake. Prvi igrač govori broj između nula i šest. Nakon toga pogađa drugi igrač. On ima više informacija jer je čuo prvog igrača, ali ne smije reći isti broj. Igrač koji je pogodio zbroj u idućem ponavljanju igre pogađa prvi, a ako nitko nije pogodio, igra se ponavlja istim redoslijedom.
Iako su pravila jednostavna, možemo postaviti nekoliko zanimljivih pitanja o ovoj igri. Pravila nisu ista za prvog i za drugog igrača, pa nije jasno je li igra poštena ili nije. Čini se da prednost ima drugi igrač, jer ima više informacija kad pogađa zbroj. Tome u prilog ide pravilo prema kojem pobjednik u idućoj igri pogađa prvi. Prvi igrač može pokušati prevariti drugog "blefiranjem", na primjer tako da u šaku zatvori tri novčića i kaže broj nula. Isplati li se prvom igraču kao dio svoje strategije povremeno blefirati? Da bismo odgovorili na ova pitanja, postavimo igru u okviru modela teorije igara.
Na prvi pogled čini se da je igra vrlo različita od prethodnih primjera. Do sada su igrači odluke uvijek donosili istovremeno i nisu imali informaciju o protivnikovom izboru. U igri giapponese i u svim igrama u kojima igrači naizmjence vuku poteze njihove odluke ovise o prethodnom tijeku igre. Treba razlikovati poteze od strategija. Strategije u sebi uključuju odgovor na svaki protivnikov potez u bilo kojem trenutku igre.
U igri giapponese prvi igrač donosi dvije odluke: koliko novčića
zatvoriti u šaku i koji broj reći. Njegove čiste strategije možemo
identificirati s parovima (x, y), pri čemu je x
broj iz skupa {0,1,2,3}, a y iz skupa {0,1,2,3,4,5,6}. Na prvoj
koordinati imamo 4 moguća izbora, na drugoj 7, pa prvi igrač
ima ukupno 4 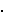 7 = 28
čistih strategija. Drugi igrač donosi iste odluke, ali broj koji će
reći ovisi o broju koji je rekao prvi igrač. Njegovu drugu odluku
identificiramo s funkcijom f : {0,1,2,3,4,5,6}
7 = 28
čistih strategija. Drugi igrač donosi iste odluke, ali broj koji će
reći ovisi o broju koji je rekao prvi igrač. Njegovu drugu odluku
identificiramo s funkcijom f : {0,1,2,3,4,5,6}
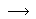 {0,1,2,3,4,5,6}. Ako prvi
igrač kaže broj y, drugi igrač govori f (y).
Po pravilima igre brojevi y i f (y) moraju
biti različiti, tj. funkcija f ne smije imati fiksnu točku.
Takvih funkcija ima 67 = 279936. Prema
tome, ukupan broj čistih strategija drugog igrača je
4
{0,1,2,3,4,5,6}. Ako prvi
igrač kaže broj y, drugi igrač govori f (y).
Po pravilima igre brojevi y i f (y) moraju
biti različiti, tj. funkcija f ne smije imati fiksnu točku.
Takvih funkcija ima 67 = 279936. Prema
tome, ukupan broj čistih strategija drugog igrača je
4 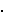 279936 = 1119744.
279936 = 1119744.
Matrica isplata igre giapponese ima 28 redaka i više od milijun stupaca. Odgovarajući problemi linearnog programiranja sadrže previše varijabli za rješavanje pomoću Mathematice. Na istu bi zapreku naišli kod analiziranja bilo koje imalo složenije igre. Na primjer, broj čistih strategija igre šah nezamislivo je velik. Šah sa stanovišta teorije igara zapravo nije jako zanimljiv, jer je kao i sve ostale igre s potpunom informacijom strogo određena igra. Jedan od igrača (vjerojatno prvi) ima pobjedničku strategiju koju treba uvijek slijediti ili postoje strategije koje igračima uvijek omogućuju remi. Na sreću mnogih šahista, današnja računala nisu dovoljno snažna za određivanje optimalnih šahovskih strategija.
Sa stanovišta teorije igara zanimljivije su igre s nepotpunom informacijom, na primjer poker i bridge. One vrlo vjerojatno nisu strogo određene. Zbog prevelikog broja čistih strategija ni te dvije igre nije moguće potpuno analizirati. Međutim, analizirane su razne pojednostavljene verzije, a to nam može nešto reći o pravoj igri. Tako ćemo i mi postupiti.
Promotrimo varijantu igre giapponese u kojoj svaki
igrač ima samo jedan novčić. Čiste strategije prvog
igrača su parovi (x, y) za x
iz {0,1} i y iz {0,1,2}; ima ih 6. Čiste
strategije drugog igrača su parovi (x, f ),
gdje je x iz {0,1}, a f : {0,1,2}
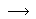 {0,1,2} je funkcija
bez fiksne točke. Takvih funkcija ima 23
= 8, pa drugi igrač ima ukupno
2
{0,1,2} je funkcija
bez fiksne točke. Takvih funkcija ima 23
= 8, pa drugi igrač ima ukupno
2 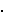 8 = 16 čistih
strategija. Element matrice isplata u retku označenim s
(x1, y) i stupcu
označenim s (x2, f )
jednak je 1 ako je
x1 + x2 = y;
ako je x1 + x2 = f (y)
jednak je -1, a inače je 0. U prvom slučaju pobjeđuje prvi igrač, u
drugom drugi, a u trećem je neodlučeno. Cijelu matricu konstruirat
ćemo s nekoliko Mathematica naredbi.
8 = 16 čistih
strategija. Element matrice isplata u retku označenim s
(x1, y) i stupcu
označenim s (x2, f )
jednak je 1 ako je
x1 + x2 = y;
ako je x1 + x2 = f (y)
jednak je -1, a inače je 0. U prvom slučaju pobjeđuje prvi igrač, u
drugom drugi, a u trećem je neodlučeno. Cijelu matricu konstruirat
ćemo s nekoliko Mathematica naredbi.

Čitaocu prepuštamo formulirati pripadne probleme linearnog programiranja i riješiti ih. Doći će do neočekivanog zaključka da je giapponese ipak poštena igra. Objašnjenje ovog fenomena također ostavljamo za zadatke.
|
|
|
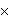 2 igre. Ako je izraz
N = a + d - b - c iz nazivnika jednak nuli,
dokažite da matrica isplata ima sedlastu točku.
2 igre. Ako je izraz
N = a + d - b - c iz nazivnika jednak nuli,
dokažite da matrica isplata ima sedlastu točku.