
Broj 1




















Ivan Štedul
Algebarska metoda rješavanja konstruktivnih zadaća

Sadržaj:
Algebarska metoda rješavanja konstruktivnih zadaćaKonstruiranje osnovnih algebarskih izraza
Primjena algebarske metode u konstruktivnim zadaćama
Zaključak
Zadatci za vježbu
Literatura
Algebarska metoda rješavanja konstruktivnih zadaća
Riješiti konstruktivni zadatak znači na osnovi onoga što je u njemu dano konstruirati figuru koja se traži, upotrebljavajući pritom samo šestar i ravnalo s jednim bridom. Pri rješavanju konstruktivnih zadaća jednobridnim ravnalom i šestarom koristimo se raznim metodama. Neke od najčešće korištenih metoda geometrijskog konstruiranja su metoda presjeka skupova točaka odnosno metoda geometrijskih mjesta točaka, metoda pomoćnih likova i metoda geometrijskih transformacija. O tim metodama više možete doznati u [1]. Međutim ponekad se dogodi da niti jednom od spomenutih metoda geometrijskog konstruiranja, bez obzira koliko se trudili, ne možemo riješiti neki konstruktivni zadatak. Tada možemo pokušati naš konstruktivni zadatak riješiti primjenom algebarske metode rješavanja konstruktivnih zadaća.Za daljnje razumijevanje teksta potrebno je poznavati neke temeljne konstrukcije ravnalom i šestarom (prijenos dužina, konstrukcija simetrale i polovišta dužine, konstrukcija simetrale kuta i polovišta luka, konstrukcija pravca koji prolazi danom točkom i koji je paralelan s danim pravcem, konstrukcija okomice na dani pravac i dr.)
Znamo da se svaki matematički zadatak, pa tako i konstruktivni, sastoji od danih ili poznatih i traženih ili nepoznatih veličina odnosno objekata, te od uvjeta koji opisuju odnose i veze između poznatih i nepoznatih veličina i objekata. Naravno da u konstruktivnim zadaćama nepoznate veličine treba konstruirati. Bit algebarske metode rješavanja konstruktivnih zadaća je u tome da se nepoznate veličine, dakle one koje treba konstruirati, izraze algebarskim izrazima odnosno formulama pomoću danih veličina. Nakon toga se dobiveni izrazi konstruiraju.
Na primjer, neka su u našoj konstruktivnoj zadaći dane dužine a, b, c, ... , k i redom njihove duljine a, b, c, ... , k, i neka je za rješenje zadaće potrebno konstruirati dužinu x nepoznate duljine x. Kao što smo već rekli, sada duljinu x tražene dužine x izrazimo nekim algebarskim izrazom odnosno formulom pomoću danih veličina:
x = f(a,b,c,...,k).
Napomena: Kako su duljine dužina uvijek pozitivne vrijednosti, to i gornji izraz f ima smisla samo ako poprima pozitivne vrijednosti. Zapravo, mi razmatramo samo pozitivne vrijednosti izraza f.I na kraju, konstruiranjem izraza f zapravo konstruiramo dužinu x, a time je konstruktivna zadaća riješena.
Konstruiranje osnovnih algebarskih izraza
U praksi se često događa da dobiveni izraz f nerijetko bude vrlo složenog oblika. Stoga je da bismo konstruirali složene algebarske izraze, dobro znati konstruirati neke jednostavnije izraze koji se lako konstruiraju. Te ćemo izraze zvati osnovnim izrazima. Na konstrukcijama osnovnih izraza zapravo se temelji primjena algebarske metode u rješavanju konstruktivnih zadaća. Zato ćemo na početku najprije reći nekoliko riječi o tim konstrukcijama.1. x = a + b, (zbrajanje dužina).
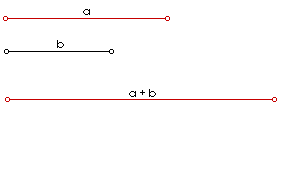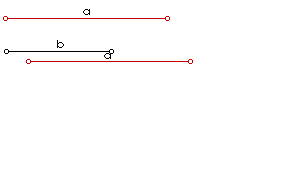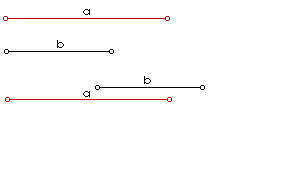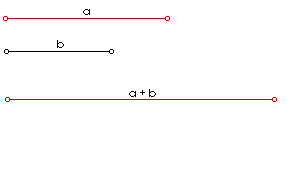
Neka su zadane dvije dužine a i b, čije su duljine a i b. Dužinu x, kako se na slici 1. vidi, dobijemo ako na isti pravac nanesemo dužinu a i zatim dužinu b tako da te dvije dužine imaju samo jednu krajnju točku zajedničku. Prema slici razabiremo dužinu duljine x = a + b.
|
| Slika 1. Animirani prikaz zbrajanja dužina |
I ovdje na pravac nanesemo dužinu a, a zatim i dužinu b, ali tako da im se jedna krajnja točka poklapa i da postoje nutarnje preklopljene točke. Rezultat x = a - b razabire se prema slici 2.
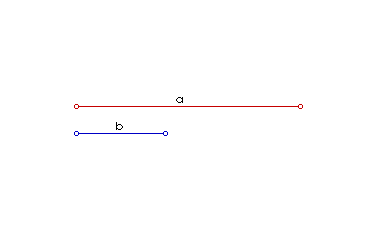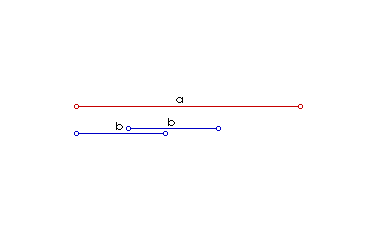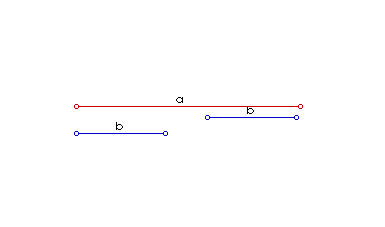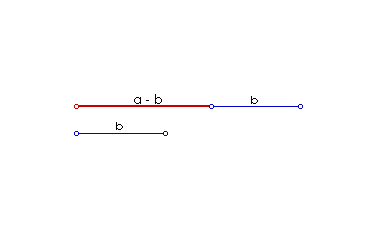
|
| Slika 2. Animirani prikaz oduzimanja dužina |
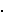 a,
n je prirodan broj, (množenje dužine
prirodnim brojem).
a,
n je prirodan broj, (množenje dužine
prirodnim brojem).
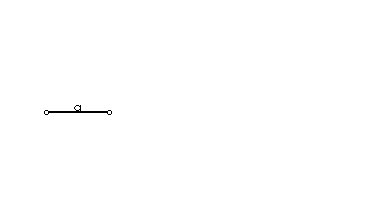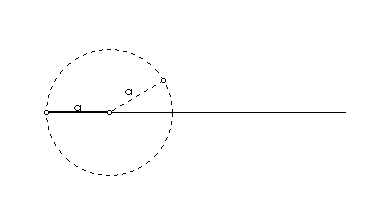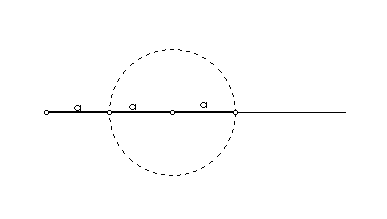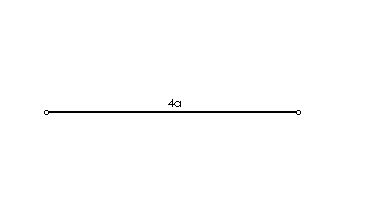
|
| Slika 3. Animirani prikaz množenja dužine prirodnim brojem |
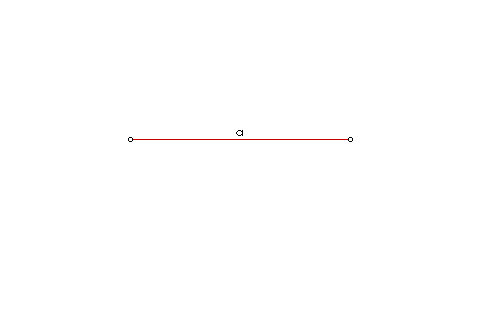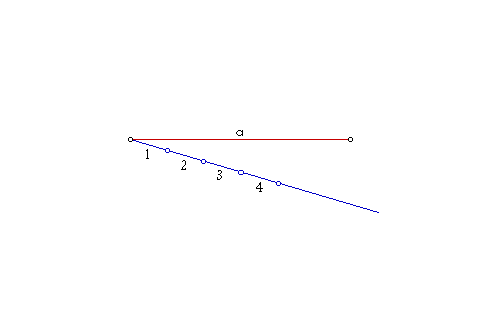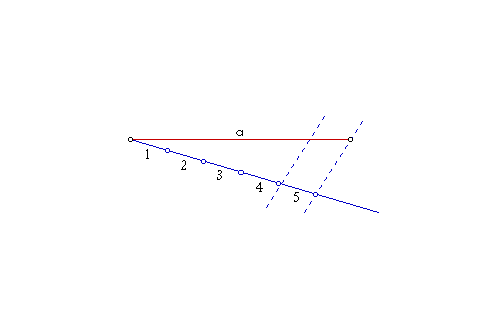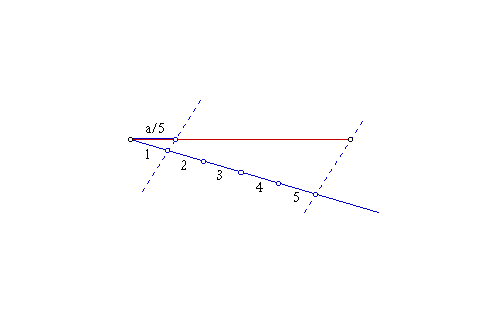
|
| Slika 4. Animirani prikaz dijeljenja dužine prirodnim brojem |
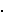 b. (Na slici 4.
prikazana je konstrukcija dijeljenja dužine prirodnim brojem za
n=5.)
Sada kroz točku B1
povučemo paralelu sa spojnicom AB.
Ta paralela siječe dužinu
OA
u točki A1 i
|OA1|
= |OA|
/ n.
5.
b. (Na slici 4.
prikazana je konstrukcija dijeljenja dužine prirodnim brojem za
n=5.)
Sada kroz točku B1
povučemo paralelu sa spojnicom AB.
Ta paralela siječe dužinu
OA
u točki A1 i
|OA1|
= |OA|
/ n.
5.
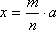 ,
m i n su prirodni brojevi (množenje
dužine racionalnim brojem).
,
m i n su prirodni brojevi (množenje
dužine racionalnim brojem).
Konstrukcija se svodi na 3. i 4.
Prvo se konstruira izraz
x1 = a / n,
a onda x = m
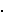 x1.
x1.
6.
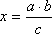 ,
(četvrta proporcionala).
,
(četvrta proporcionala).
Ovaj je izraz vrlo važan u algebarskoj metodi konstruiranja pa ćemo stoga pokazati dva načina konstruiranja ovog izraza.
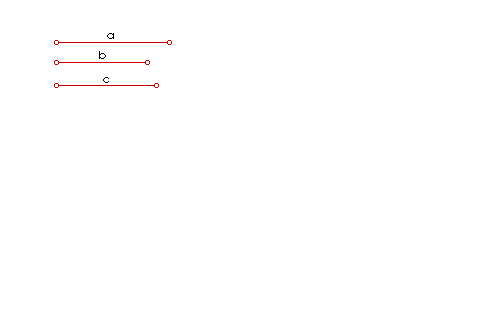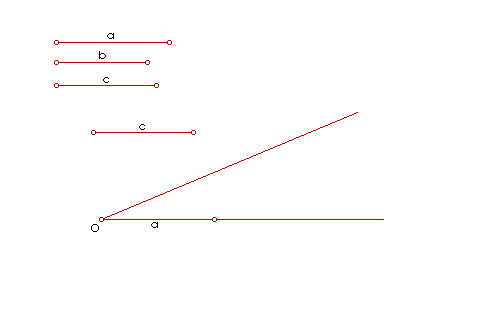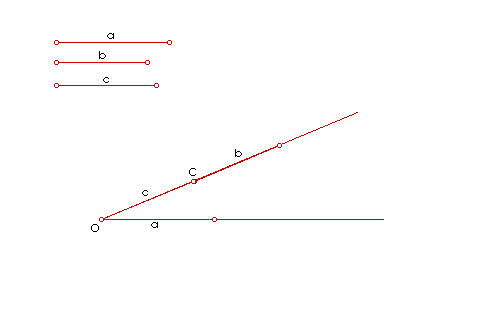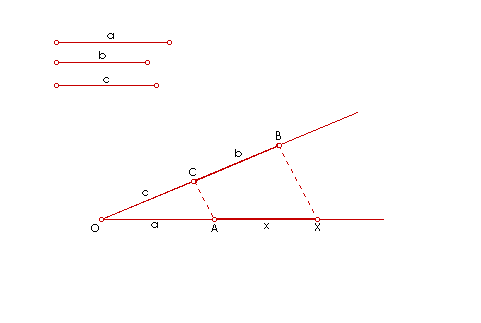
|
| Slika 5. Animacija četvrte proporcionale I. |
Dokaz konstrukcije: Da bismo dokazali konstrukciju, potreban nam je iskaz Talesovog poučka o proporcionalnim dužinama.
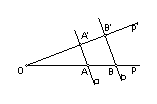
|
| Slika 6. Talesov poučak o proporcionalnim dužinama |
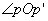 odsijecaju proporcionalne dužine:
odsijecaju proporcionalne dužine:
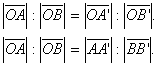
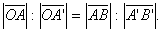
Sada je prema Talesovom poučku
očito x : b = a : c,
a odavde je
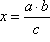 .
.
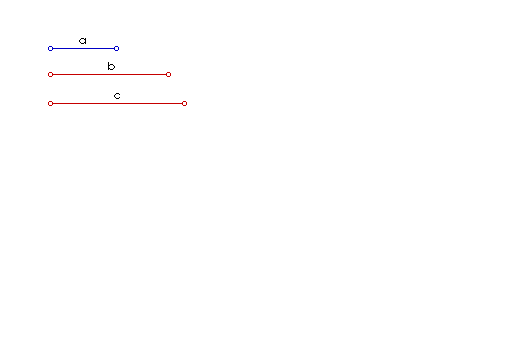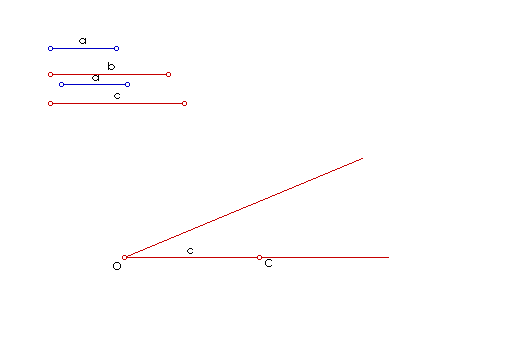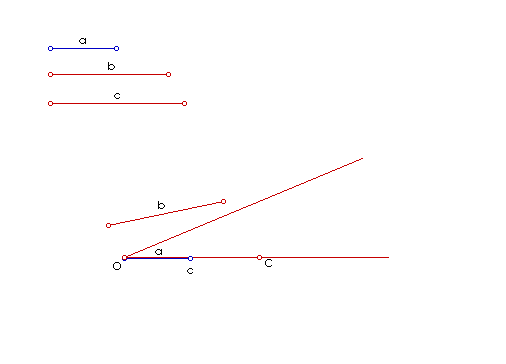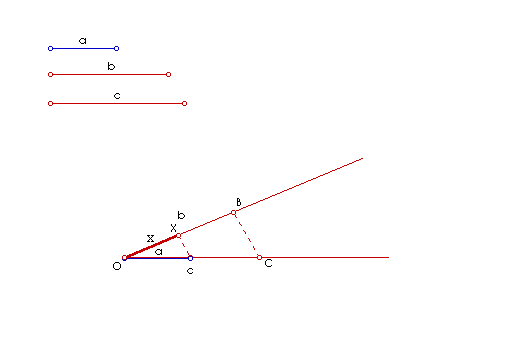
|
| Slika 7. Animacija četvrte proporcionale II. |
Dokaz konstrukcije:
Po konstrukciji je
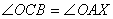 i
i
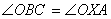 ,
pa slijedi da su trokuti
,
pa slijedi da su trokuti
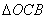 i
i
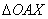 slični. Zbog sličnosti je
slični. Zbog sličnosti je
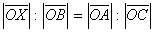 ,
a to je upravo x : b = a : c.
Odavde slijedi
,
a to je upravo x : b = a : c.
Odavde slijedi 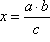 .
Dokaz smo također mogli izravno direktno iz Talesovog
poučka o proporcionalnosti dužina.
.
Dokaz smo također mogli izravno direktno iz Talesovog
poučka o proporcionalnosti dužina.
7.
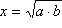 ,
(geometrijska sredina brojeva a i b).
,
(geometrijska sredina brojeva a i b).

|
| Slika 8. Animacija geometrijske sredine |
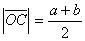 .
U točki B podignemo okomicu na zraku AC koja
siječe polukružnicu k u točki X.
.
U točki B podignemo okomicu na zraku AC koja
siječe polukružnicu k u točki X.
Tvrdnja: dužina BX duljine x je tražena dužina.
Da bismo dokazali tvrdnju, iskažimo Talesov poučak o kutu nad promjerom kružnice: Svaki kružnici upisan trokut nad promjerom kružnice je pravokutan.
Dokaz: Prema Talesovom poučku o kutu nad promjerom kružnice
vrijedi da je
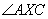 pravi kut. Stoga su trokuti
pravi kut. Stoga su trokuti
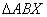 i
i
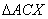 slični jer su im svi kutovi jednaki. Trokuti
slični jer su im svi kutovi jednaki. Trokuti
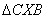 i
i
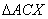 također su slični. Stoga zaključujemo da su
također su slični. Stoga zaključujemo da su
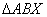 i
i
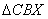 slični (tranzitivnost relacije ˝biti sličan˝), pa vrijedi:
slični (tranzitivnost relacije ˝biti sličan˝), pa vrijedi:
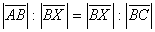 ,
,
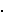 b,
te
b,
te 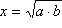 .
.
8.
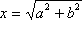 .
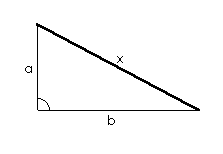
Iz Pitagorinog poučka slijedi da je dužina duljine
x hipotenuza pravokutnog
trokuta kojemu su katete dužine
a i
b
(slika 9.).
.
Iz Pitagorinog poučka slijedi da je dužina duljine
x hipotenuza pravokutnog
trokuta kojemu su katete dužine
a i
b
(slika 9.).
|
|
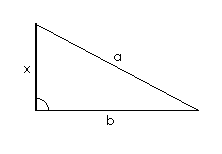
| Slika 9. Pravokutan trokut I. | Slika 10. Pravokutan trokut II. |
9.
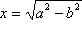 ,
(a > b). Tu je dužina
x
očito kateta pravokutnog trokuta kojemu je druga kateta
b,
a hipotenuza
a
(slika 10.).
,
(a > b). Tu je dužina
x
očito kateta pravokutnog trokuta kojemu je druga kateta
b,
a hipotenuza
a
(slika 10.).
Sada kad znamo konstruirati neke jednostavnije izraze, možemo konstruirati i mnogo složenije izraze tako da ih raščlanimo u niz jednostavnih konstrukcija koje smo upravo opisali. Pogledajmo par jednostavnijih primjera.
Primjer 1.
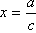 .
Konstrukcija se svodi na konstrukciju
četvrte proporcionale za b = 1.
.
Konstrukcija se svodi na konstrukciju
četvrte proporcionale za b = 1.
Primjer 2.
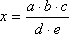 .
Dani izraz možemo rastaviti na dva jednostavnija izraza,
.
Dani izraz možemo rastaviti na dva jednostavnija izraza,
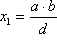 i
i
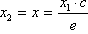 .
Sada primjenom
konstrukcije 6. rješavamo zadatak.
.
Sada primjenom
konstrukcije 6. rješavamo zadatak.
Primjer 3.
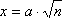 ,
n je prirodan broj. Konstrukciju ćemo riješiti na tri načina.
,
n je prirodan broj. Konstrukciju ćemo riješiti na tri načina.
- Gornji izraz možemo zapisati u obliku
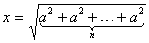 .
Primjenom n – 1 konstrukcija 8. na izraze
.
Primjenom n – 1 konstrukcija 8. na izraze
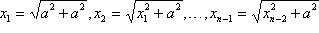 dobivamo traženu konstrukciju.
dobivamo traženu konstrukciju. -
Ako je n = p
 q, gdje su p i q prirodni brojevi, onda
gornji izraz možemo prikazati u obliku
q, gdje su p i q prirodni brojevi, onda
gornji izraz možemo prikazati u obliku
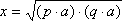 .
Sada izraze x1 = p
.
Sada izraze x1 = p
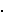 a i
x2 = q
konstruiramo konstrukcijom 3.
Gornji izraz sada možemo zapisati u obliku
a i
x2 = q
konstruiramo konstrukcijom 3.
Gornji izraz sada možemo zapisati u obliku
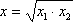 i konstruirati primjenom konstrukcije 7.
i konstruirati primjenom konstrukcije 7. -
Općenito, ako je n = p2 +
q2, gdje su p i q
prirodni brojevi, gornji izraz možemo napisati u obliku
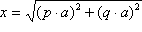 ,
što se svodi na konstrukcije 3. i 8.
,
što se svodi na konstrukcije 3. i 8.
|
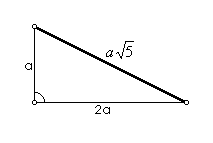
|
Slika 11. Konstrukcija
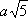 I.
I.
|
Slika 13. Konstrukcija
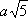 III.
III.
|

|
|
Slika 12. Konstrukcija
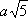 II.
II.
|
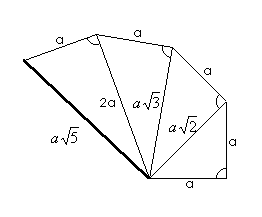
Na slici 11. prikazan je prvi način konstrukcije
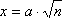 ,
n = 5.
Na slici 12. prikazan je drugi način iste konstrukcije,
a na slici 13. treći.
,
n = 5.
Na slici 12. prikazan je drugi način iste konstrukcije,
a na slici 13. treći.
Primjer 4.
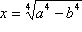 ,
(a > b).
Ovaj izraz možemo napisati u obliku:
,
(a > b).
Ovaj izraz možemo napisati u obliku:
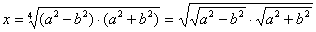
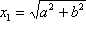 i
i
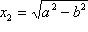 ,
a odatle primjenom konstrukcije 7. konstruiramo
,
a odatle primjenom konstrukcije 7. konstruiramo
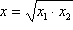 .
.
Pitanje koje se sada prirodno nameće je može li se svaki algebarski izraz konstruirati. Na to pitanje odgovara nam sljedeći poučak čiji dokaz preskačemo.
Teorem 1. Svaki onaj izraz koji dobijemo iz danih dužina konačnim brojem operacija (zbrajanjem, oduzimanjem, množenjem, dijeljenjem) i vađenjem kvadratnog korijena, može se konstruirati.
Primjena algebarske metode u konstruktivnim zadaćama
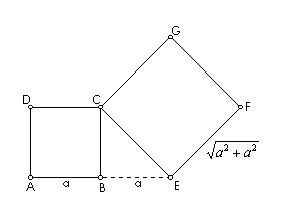
Zadatak 1. Konstruirajte kvadrat čija je površina dvostruko veća od površine danog kvadrata.
Analiza: Pretpostavimo da je zadatak riješen (slika 14.). Neka je ABCD zadani kvadrat sa stranicom duljine a, a CEFG traženi kvadrat. Označimo s x duljinu stranice traženog kvadrata. Iz uvjeta zadatka P(CEFG) = 2P(ABCD) dobivamo x2 = 2a2, odakle slijedi da je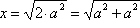 .
.
|
| Slika 14. Dvostruko veći kvadrat |
Konstrukcija: Iz analize je vidljivo da za
rješenje zadatka moramo konstruirati izraz
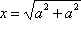 ,
što lako konstruiramo primjenom konstrukcije 8. Dan
je kvadrat ABCD. Na zraku AB iz točke B
nanesemo dužinu
BE
duljine a. Nad stranicom
CE
konstruiramo traženi kvadrat CEFG.
,
što lako konstruiramo primjenom konstrukcije 8. Dan
je kvadrat ABCD. Na zraku AB iz točke B
nanesemo dužinu
BE
duljine a. Nad stranicom
CE
konstruiramo traženi kvadrat CEFG.
Dokaz: Iz
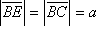 i iz
Pitagorinog poučka slijedi da je duljina stranice kvadrata
CEFG jednaka
i iz
Pitagorinog poučka slijedi da je duljina stranice kvadrata
CEFG jednaka
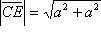 .
.
Zadatak 2. Zadan je polukrug k polumjera r. U tu figuru upišite kvadrat.
Analiza: Dana je polukružnica k sa središtem u točki O i polumjera r (slika 15.). ABCD je traženi kvadrat. Označimo duljinu njegove stranice s x. Sa slike je očito da je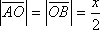 ,
te iz Pitagorina poučka primijenjenog na trokut
,
te iz Pitagorina poučka primijenjenog na trokut
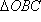 dobivamo
dobivamo
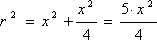 .
Odavde dobivamo da je
.
Odavde dobivamo da je
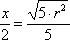 .
.
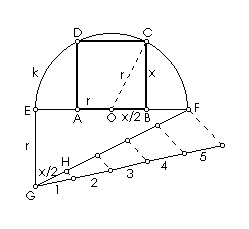
|
| Slika 15. Kvadrat upisan u polukružnicu |
Konstrukcija: Za rješenje
zadatka potrebno je konstruirati dužinu duljine
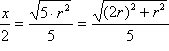 .
Prvo konstruiramo izraz
.
Prvo konstruiramo izraz
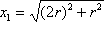 primjenom konstrukcije 8. Iz točke E
povučemo okomicu na EF i na nju nanesemo dužinu
EG
duljine r. Sada konstruiramo izraz
primjenom konstrukcije 8. Iz točke E
povučemo okomicu na EF i na nju nanesemo dužinu
EG
duljine r. Sada konstruiramo izraz
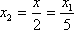 primjenom konstrukcije 4. Dakle, dužinu
FG
primjenom konstrukcije 4. podijelimo na 5 jednakih dijelova,
svaki tražene duljine. Uzmemo u šestar duljinu
primjenom konstrukcije 4. Dakle, dužinu
FG
primjenom konstrukcije 4. podijelimo na 5 jednakih dijelova,
svaki tražene duljine. Uzmemo u šestar duljinu
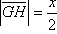 i oko točke O na EF označimo šestarom točke
A i B. Okomice iz A i B
na EF sijeku polukružnicu k u D i C.
ABCD je traženi kvadrat.
i oko točke O na EF označimo šestarom točke
A i B. Okomice iz A i B
na EF sijeku polukružnicu k u D i C.
ABCD je traženi kvadrat.
Dokaz: Trokut
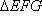 je pravokutan po konstrukciji, pa iz Pitagorinog poučka slijedi
da je
je pravokutan po konstrukciji, pa iz Pitagorinog poučka slijedi
da je
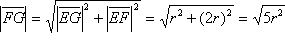 .
Sada je po konstrukciji očito
.
Sada je po konstrukciji očito
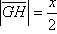 ,
što je i trebalo dokazati.
,
što je i trebalo dokazati.
Zadatak 3. Dan je trokut
 Oko vrhova danog trokuta treba opisati kružnice koje se u
parovima izvana dodiruju.
Oko vrhova danog trokuta treba opisati kružnice koje se u
parovima izvana dodiruju.
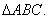 .
S A, B i C označili smo vrhove trokuta,
s a, b i c,
a s x, y i z
polumjere traženih kružnica. Sa slike 16.
odmah se vidi da vrijedi x + y = c,
y + z = a i x + z = b.
Rješenja ovog sustava triju linearnih jednadžbi s tri
nepoznanice su:
.
S A, B i C označili smo vrhove trokuta,
s a, b i c,
a s x, y i z
polumjere traženih kružnica. Sa slike 16.
odmah se vidi da vrijedi x + y = c,
y + z = a i x + z = b.
Rješenja ovog sustava triju linearnih jednadžbi s tri
nepoznanice su:
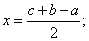
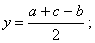
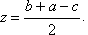
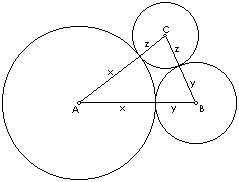
|
| Slika 16. Kružnice koje se dodiruju |
Konstrukcija: Primjenom konstrukcija 1. 2. i 4. najprije konstruiramo jednu od veličina danih gornjim izrazima, npr. x: x1 = b + c, x2 = x1 - a, x3 = x = x2 / 2. Sada se oko točaka A, B i C opišu kružnice polumjera x, c - x i b - x.
Dokaz slijedi iz analize.
Diskusija: Konstrukcija je jedinstvena. Treba još pokazati da je uvijek izvediva, tj. da su x, y i z strogo pozitivne veličine. To slijedi iz nejednakosti trokuta: a + b > c, a + c > b i b + c > a.
Zadatak 4. U kvadrat s duljinom stranice a upišimo pet kružnica jednakih polumjera tako da četiri od njih dodiruju po dvije stranice kvadrata, a peta ove četiri kružnice.
Analiza: Sa slike 17. očito je da su središta kružnica na dijagonalama kvadrata, pa preostaje samo odrediti njihov polumjer x. Središta donje tri kružnice su vrhovi pravokutnog trokuta s katetama duljina 2x, 2x i hipotenuzom duljine a - 2x, pa iz Pitagorinog poučka dobivamo 4x2 + 4x2 = a2 - 4ax + 4x2, odakle dobivamo da je
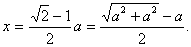
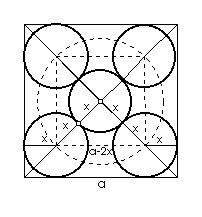
|
| Slika 17. Pet kružnica u kvadratu |
Konstrukcija:
Gornji izraz za x lako konstruiramo primjenom
konstrukcija 8. 2. i 4.
redom na izraze
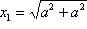 ,
,
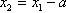 i
i
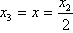 .
Sada danim polumjerom konstruiramo prvu kružnicu sa
središtem u sjecištu dijagonala kvadrata. Središta ostale 4 kružnice dobijemo
kao sjecišta dijagonala i kružnice s istim središtem
kao i prva kružnica, polumjera 2x.
.
Sada danim polumjerom konstruiramo prvu kružnicu sa
središtem u sjecištu dijagonala kvadrata. Središta ostale 4 kružnice dobijemo
kao sjecišta dijagonala i kružnice s istim središtem
kao i prva kružnica, polumjera 2x.
Dokaz slijedi iz analize. Zadatak je uvijek određen i ima jedinstveno rješenje.
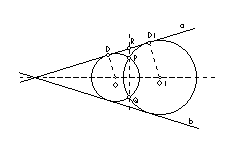
Zadatak 5. Dani su ukršteni pravci a i b, i točka P unutar jednog kuta tih pravaca. Konstruirajmo kružnicu koja prolazi točkom P i dira pravce a i b.
Analiza: Pretpostavimo da je zadatak riješen (slika 18.) Točka Q kojom također mora prolaziti tražena kružnica leži simetrično točki P s obzirom na simetralu kuta što ga zatvaraju dani pravci a i b. Misli se na simetralu kuta koja leži u kutu zajedno s danom točkom P. Spojnica PQ pri tome je okomita na simetralu kuta. Označimo s R sjecište spojnice PQ s pravcem a, a s D diralište tražene kružnice također s pravcem a. Tada prema poučku o potenciji točke imamo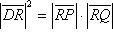 ,
a odatle
,
a odatle
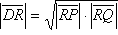 .
.
|
| Slika 18. Kružnica danom točkom koja dira dva pravca |
Konstrukcija: Dobiveni izraz
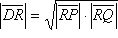 lako konstruiramo primjenom konstrukcije 7. Sada točku
D dobijemo kao presjek
kružnice sa središtem u točki R, polumjera
|DR|
s pravcem a.
Presjek okomice iz točke D na a
i simetrale kuta koji zatvaraju pravci a i b
jest točka O koja je središte tražene kružnice.
lako konstruiramo primjenom konstrukcije 7. Sada točku
D dobijemo kao presjek
kružnice sa središtem u točki R, polumjera
|DR|
s pravcem a.
Presjek okomice iz točke D na a
i simetrale kuta koji zatvaraju pravci a i b
jest točka O koja je središte tražene kružnice.
Dokaz slijedi iz analize. Zadaća uvijek ima dva rješenja.
Zaključak
Dakako da se svaki konstruktivni zadatak ne može uvijek riješiti algebarskom metodom rješavanja konstruktivnih zadaća, ali, kao što smo vidjeli, daje nam mogućnost više njihovo za rješavanje. Dapače, katkad, kad ni na jedan drugi način ne možemo riješiti neku konstruktivnu zadaću, algebarska metoda može ˝spasiti situaciju˝. Zato je vrlo dobro poznavati njezine osnovne konstrukcije pa nam mnoge konstruktivne zadaće više neće zadavati glavobolje.Zadatci za vježbu
- Zadatak. Konstruirajte
kvadrat kojemu je površina jednaka zbroju površina dvaju danih
pravokutnika.
- Zadatak. Zadan je trokut
 .
Konstruirajte kvadrat koji ima površinu jednaku
površini danog trokuta.
.
Konstruirajte kvadrat koji ima površinu jednaku
površini danog trokuta.
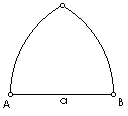
|
| Slika 19. Gotska figura |
- Zadatak.
Razdijelite dužinu
AB
točkom Z na dva dijela tako da se čitava dužina
odnosi prema većem dijelu kao veći dio prema manjem dijelu
(Zlatni rez).
- Zadatak.
Povucite pravac paralelan dijagonali danog pravokutnika ABCD
tako da on dijeli taj pravokutnik na dva dijela čije se površine
odnose kao 1 : 4.
- Zadatak. Dužina AB duljine a i lukovi kružnica k1(A,a) i k2(B,a) čine konveksnu figuru (slika 19). Upišite u tu figuru kružnicu.
Literatura
[1] B. Jagodić, N. Sarapa, Matematika 7 - udžbenik za 7. razred osnovne škole, Školska knjiga, Zagreb, 1998.[2] D. Palman, Geometrijske konstrukcije, Element, Zagreb, 1996.
[3] B. Pavković, D. Veljan, Elementarna matematika 1, Tehnička knjiga, Zagreb 1992.
[4] M. Pavleković, Nastava matematike s informatikom I, Element, Zagreb, 1997.
Algebarska metoda rješavanja konstruktivnih zadaća
Konstruiranje osnovnih algebarskih izraza
Primjena algebarske metode u konstruktivnim zadaćama
Zaključak
Zadatci za vježbu
Literatura