
Hrvatski matematički elektronski časopis math.e

|
Hrvatski matematički elektronski časopis math.e |
| http://www.math.hr/~mathe/ |
Popločavanja ravnine
Kristina Krulić
1. Problem popločavanja ravnine
2. Pravilna popločavanja ravnine
3. Arhimedova popločavanja ravnine
4. Zaključak
Literatura
Ukrašavanje životnog prostora oduvijek je bila ljudska praksa, od prvobitnih spilja, velebnih egipatskih građevina pa do danas. Razvojem i napretkom ljudske kulture razvija se umjetnost i potreba za lijepim i skladnim sve više dolazi do izražaja. Mnogi crteži prikazuju predmete iz života i prirode, a na nekima možemo uočiti figure koje se periodički ponavljaju, poprimaju geometrijske oblike s mnogo simetrije i pokazuju pravilnost kakvu u prirodi rijetko susrećemo. Tako je pomalo od slobodnih crteža nastao ornament. Stvaralac takvih crteža morao je s estetskim ukusom sjediniti i stanovito geometrijsko znanje. Javlja se i potreba za ukrašavanjem zidova i podova. Njih, također, možemo ukrasiti pravilnim geometrijskim figurama.
Problem popločavanja ili parketiranja drevni je problem koji možemo naći kod starih Egipćana, Perzijanaca, Grka, Rimljana, a također u Kini, Japanu te u drugim starim civilizacijama. Što je to problem parketiranja, tj. popločavanja ravnine? Treba razdijeliti ravninu na mnogokute koji bi je u potpunosti prekrivali, bez praznina i preklapanja, uz određene pravilnosti s obzirom na vrstu, oblik i poredak mnogokuta.
Razdiobu ravnine na pravilne mnogokute možemo vidjeti na ulicama, trgovima i na mnogim umjetničkim slikama. Time se pokazuje da matematika i umjetnost imaju mnogo toga zajedničkog iako neki misle da su upravo na suprotnim krajevima širokog i bogatog spektra ljudskih djelatnosti.
Prije razmatranja problema popločavanja treba uvesti neke osnovne pojmove.
|
Particija skupa K je familija nepraznih, međusobno disjunktnih podskupova od
K kojima je unija čitav |
Zanimaju nas rastavi ravnine na mnokogute koji imaju zajedničke stranice i vrhove, a unutrašnjosti su im disjunktne. Takve rastave također ćemo zvati razdiobama ili particijama. Mnogokute koji se sijeku u vrhovima ili stranicama nazivamo susjednim mnogokutima. Točku ravnine u kojoj se sastaju vrhovi susjednih mnogokuta nazivamo čvorištem particije. Ako su svi kutovi mnogokuta koji se sastaju u jednom čvorištu međusobno sukladni, onda takvo čvorište nazivamo pravilnim čvorištem. Također, kažemo da su dva čvorišta sukladna ako je slijed kutova koji se u njemu sastaju isti. Problem koji se postavlja jest pronaći sve moguće razdiobe, tj. popločavanja ravnine pravilnim mnogokutima, pri čemu svi mnogokuti i sva čvorišta moraju biti sukladni. Takva ćemo popločavanja zvati pravilnim popločavanjima ravnine.
Pokušajmo sada ovaj geometrijski problem zapisati algebarski, tj. svesti ga na jednadžbu.
Očito, prvi uvjet koji mora biti ispunjen je da zbroj veličina kutova u svakom čvorištu
iznosi 360°. Također, znamo da zbroj
veličina unutrašnjih kutova u n-terokutu iznosi
(n-2) 180°. Budući da su u
pravilnom n-terokutu svi unutrašnji kutovi međusobno sukladni, njihova veličina
iznosi
180°. Budući da su u
pravilnom n-terokutu svi unutrašnji kutovi međusobno sukladni, njihova veličina
iznosi
(n-2) 180° 180°n |
. |
Vratimo se sada postavljenom problemu. Ako se u svakom čvorištu sastaje k pravilnih n-terokuta, onda upravo postavljeni uvjet možemo izraziti diofantskom jednadžbom
k  |
(n-2) 180° 180°n |
= 360°, | (1) |
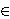
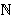 i n
i n 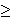 3
(mnogokut s najmanjim brojem stranica je trokut). Znači, problem pravilnog
popločavanja ravnine sveli smo na rješavanje diofantske jednadžbe. Rezultat
je dan sljedećim teoremom.
3
(mnogokut s najmanjim brojem stranica je trokut). Znači, problem pravilnog
popločavanja ravnine sveli smo na rješavanje diofantske jednadžbe. Rezultat
je dan sljedećim teoremom.
| Teorem 1. Jedina pravilna popločavanja ravnine su na jednakostranične trokute, kvadrate i pravilne šesterokute, i to tako da ih se u jednom čvorištu sastaje po šest, četiri, odnosno po tri. |
Dokaz. Da bismo dokazali ovaj teorem, potrebno je riješiti diofantsku
jednadžbu (1). Njezinim skraćivanjem sa 180 te množenjem
s n dobijemo
jednadžbu k  (n - 2) = 2n.
Dalje, dijeljenjem s n - 2 slijedi
(n - 2) = 2n.
Dalje, dijeljenjem s n - 2 slijedi
| k = | 2n n - 2 |
= 2 + | 4 n - 2 | . | (2) |
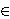 {-2,0,1,3,4,6}. Neke mogućnosti možemo odmah eliminirati jer je
n
{-2,0,1,3,4,6}. Neke mogućnosti možemo odmah eliminirati jer je
n 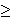 3. Ostaju samo
tri mogućnosti: n = 3 (jednakostraničan trokut), n = 4
(kvadrat) i n = 6 (pravilni šesterokut). Preostaje nam još izračunati
odgovarajuće k-ove, koje dobijemo uvrštavanjem u izraz (2).
Tako za n = 3 dobijemo k = 6, za n = 4
dobijemo k = 4, a za n = 6 dobijemo k = 3.
3. Ostaju samo
tri mogućnosti: n = 3 (jednakostraničan trokut), n = 4
(kvadrat) i n = 6 (pravilni šesterokut). Preostaje nam još izračunati
odgovarajuće k-ove, koje dobijemo uvrštavanjem u izraz (2).
Tako za n = 3 dobijemo k = 6, za n = 4
dobijemo k = 4, a za n = 6 dobijemo k = 3.
Prikažimo pravilna popločavanja ravnine!
 |
 |
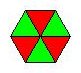
Popločavanje jednakostraničnim trokutima vidimo na slici 1. Ovo popločavanje označavamo (3,3,3,3,3,3) - redom napišemo brojeve stranica mnogokuta koji se sastaju u jednom čvorištu. Dakle, imamo šest jednakostraničnih trokuta.
 |
 |
Na slici 2 vidimo popločavanje kvadratima. Označavamo ga (4,4,4,4).
 |
 |
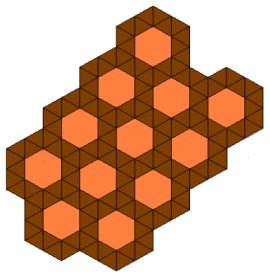
Konačno, na slici 3 prikazano je popločavanje pravilnim šesterokutima, koje označavamo (6,6,6).
Dosad smo proučavali pravilna popločavanja ravnine. Promotrimo sada slučaj kada se
u čvorištima sastaje više vrsta pravilnih mnogokuta. Za početak odredimo koliko se najviše
različitih pravilnih mnogokuta može sastajati u istoj točki. Opet postavljamo isti uvjet,
da zbroj veličina kutova u svakom čvorištu iznosi 360°. Promatramo jednakostranične
trokute, kvadrate, pravilne peterokute
i pravilne šesterokute. S  n označimo veličinu unutrašnjeg kuta pravilnog
n-terokuta. U prethodnom poglavlju koristili smo činjenicu da zbroj veličina
unutrašnjih kutova u n-terokutu iznosi (n-2)
n označimo veličinu unutrašnjeg kuta pravilnog
n-terokuta. U prethodnom poglavlju koristili smo činjenicu da zbroj veličina
unutrašnjih kutova u n-terokutu iznosi (n-2) 180°,
iz čega slijedi
180°,
iz čega slijedi
 n n |
= | (n-2) 180° 180°n | . | (3) |
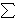
 n = 360°, gdje se sumira po
n = 3, 4, 5, 6.
Uvrštavanjem u formulu (3) vidimo da veličina unutrašnjeg kuta jednakostraničnog
trokuta iznosi
n = 360°, gdje se sumira po
n = 3, 4, 5, 6.
Uvrštavanjem u formulu (3) vidimo da veličina unutrašnjeg kuta jednakostraničnog
trokuta iznosi  3 = 60°, kvadrata
3 = 60°, kvadrata  4 = 90°, pravilnog peterokuta
4 = 90°, pravilnog peterokuta  5 = 108°, a pravilnog šesterokuta
5 = 108°, a pravilnog šesterokuta  6 = 120°. To su pravilni mnogokuti
s najmanjim brojem stranica i najmanjom veličinom unutrašnjeg kuta. Pretpostavimo
da u nekoj razdiobi ravnine jedno čvorište čine upravo ta četiri pravilna mnogokuta.
Tada je 60° + 90° + 108° + 120° = 378°, što je
veće od 360°. Ako bismo zamijenili jedan od ovih pravilnih mnogokuta
pravilnim mnogokutom s većim brojem stranica, odnosno većom veličinom
unutrašnjeg kuta, suma bi bila još veća. Zaključujemo da u razdiobi ravnine
na pravilne mnogokute ne može biti više od tri različite vrste pravilnih
mnogokuta. Time smo dokazali ovaj teorem.
6 = 120°. To su pravilni mnogokuti
s najmanjim brojem stranica i najmanjom veličinom unutrašnjeg kuta. Pretpostavimo
da u nekoj razdiobi ravnine jedno čvorište čine upravo ta četiri pravilna mnogokuta.
Tada je 60° + 90° + 108° + 120° = 378°, što je
veće od 360°. Ako bismo zamijenili jedan od ovih pravilnih mnogokuta
pravilnim mnogokutom s većim brojem stranica, odnosno većom veličinom
unutrašnjeg kuta, suma bi bila još veća. Zaključujemo da u razdiobi ravnine
na pravilne mnogokute ne može biti više od tri različite vrste pravilnih
mnogokuta. Time smo dokazali ovaj teorem.
| Teorem 2. U razdiobi ravnine na pravilne mnogokute ne može biti više od tri različite vrste pravilnih mnogokuta. |
Problem koji se postavlja jest pronaći sve moguće razdiobe, tj. popločavanja ravnine u pravilne mnogokute, pri čemu mnogokuti mogu imati različit broj stranica, ali sve stranice i sva čvorišta moraju biti sukladni. Takva ćemo popločavanja zvati Arhimedovim ili polupravilnim popločavanjima ravnine.
Pokušajmo sada razdijeliti ravninu uz tražene uvjete. Za početak uzmimo slučaj razdiobe ravnine s dvjema različitim vrstama pravilnih mnogokuta. Neka se u jednom čvorištu sastaje k1 pravilnih n1-terokuta i k2 pravilnih n2-terokuta. Nuždan uvjet je da zbroj veličina kutova oko jednog čvorišta bude 360°, što možemo zapisati diofantskom jednadžbom
| k1 |  |
(n1-2) 180° 180°n1 |
+ | k2 |  |
(n2-2) 180° 180°n2 |
= 360°, | (4) |
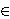
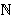 i n1, n2
i n1, n2 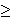 3. Ostaje nam vidjeti postoje li dodatni uvjeti
na k-ove. Znamo da je najmanji broj pravilnih mnogokuta koji čine jedno
čvorište tri (razdioba ravnine na pravilne šesterokute) pa zaključujemo da je
k1 + k2
3. Ostaje nam vidjeti postoje li dodatni uvjeti
na k-ove. Znamo da je najmanji broj pravilnih mnogokuta koji čine jedno
čvorište tri (razdioba ravnine na pravilne šesterokute) pa zaključujemo da je
k1 + k2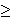 3. Također, najveći broj pravilnih mnogokuta koji
čine jedno čvorište je šest (razdioba ravnine na jednakostranične trokute)
pa je k1 + k2 < 6
(jer imamo barem jedan mnogokut koji nije trokut). Riješimo sada diofantsku
jednadžbu (4) uz opisane uvjete. Skraćivanjem sa 180 i
daljnjim sređivanjem dobivamo jednadžbu
3. Također, najveći broj pravilnih mnogokuta koji
čine jedno čvorište je šest (razdioba ravnine na jednakostranične trokute)
pa je k1 + k2 < 6
(jer imamo barem jedan mnogokut koji nije trokut). Riješimo sada diofantsku
jednadžbu (4) uz opisane uvjete. Skraćivanjem sa 180 i
daljnjim sređivanjem dobivamo jednadžbu
k1 (1/2 - 1/n1) + k2 (1/2 - 1/n1) + k2 (1/2 - 1/n2)
= 1. (1/2 - 1/n2)
= 1. | (5) |
Uz uvjet 3 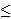 k1 + k2 < 6
za brojeve k1 i k2 imamo sljedeće mogućnosti,
koje ćemo radi preglednosti zapisati u tablici:
k1 + k2 < 6
za brojeve k1 i k2 imamo sljedeće mogućnosti,
koje ćemo radi preglednosti zapisati u tablici:
| k1 | 1 | 2 | 1 | 3 | 2 | 1 | 4 | 3 | 2 |
| k2 | 2 | 1 | 3 | 1 | 2 | 4 | 1 | 2 | 3 |
Za svaku od ovih mogućnosti rješavamo jednadžbu (5).
Uvrštavanjem vrijednosti k1 = 1 i k2 = 2 u jednadžbu (5) i sređivanjem dobivamo
| n1 | = | 2 + | 8 n2 - 4 |
. | (6) |
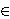 {-4,0,2,3,5,6,8,12}. S obzirom da je n2
{-4,0,2,3,5,6,8,12}. S obzirom da je n2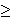 3, imamo samo pet mogućih
vrijednosti za n2. Uvrštavanjem u (6) dobivamo
n1
3, imamo samo pet mogućih
vrijednosti za n2. Uvrštavanjem u (6) dobivamo
n1 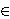 {-6,10,6,4,3}. Prva mogućnost ponovo otpada
pa imamo četiri mogućnosti za n1 i n2
ako je k1 = 1 i k2 = 2:
{-6,10,6,4,3}. Prva mogućnost ponovo otpada
pa imamo četiri mogućnosti za n1 i n2
ako je k1 = 1 i k2 = 2:
 |
 |
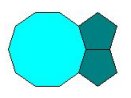
1. Krenemo od čvorišta i brojimo stranice mnogokuta koji formiraju čvorište, s time da počnemo s mnogokutom koji ima najmanji broj stranica. Uočavamo da ravninu ne možemo popločiti dvama pravilnim peterokutima i pravilnim deseterokutom jer se pri takvom popločavanju pojavljuje praznina, što nije u skladu s definicijom popločavanja.
2. Popločavanje (6,6,6) je moguće. To je popločavanje ravnine pravilnim šesterokutima koje smo vidjeli na slici 3.
 |
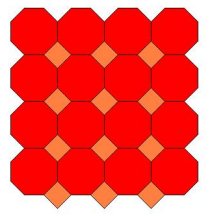 |
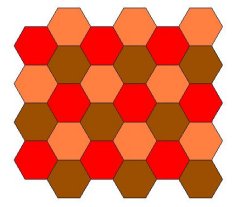
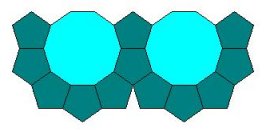
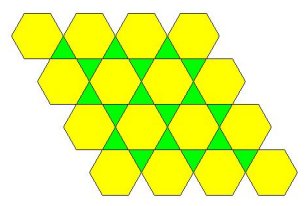
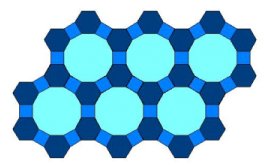
3. Popločavanje (4,8,8) prikazano je na slici 5. Ravninu možemo popločiti kvadratom i dvama pravilnim osmerokutima oko svakog čvorišta bez ikakvih praznina ili preklapanja. Uočimo također da su sva čvorišta sukladna, što je u skladu s definicijom Arhimedovog popločavanja ravnine.
 |
 |
4. Na slici 6 vidimo da se ravnina može popločiti na način (3,12,12), tj. tako da se u čvorištima sastaju jednakostraničan trokut i po dva dvanaesterokuta.
Time smo riješili prvi slučaj. Dobili smo tri rješenja: (6,6,6), (3,12,12) i (4,8,8). Za k1 = 2, k2 = 1 zaključivanje ide potpuno analogno.
Uvrštavanjem k1 = 1 i k2 = 3 u jednadžbu (5) i sređivanjem dobivamo
| n1 | = | 1 + | 3 n2 - 3 |
. | (7) |
 3 pa za k1 = 1,
k2 = 3 dobivamo samo popločavanje ravnine
kvadratima prikazano na slici 2.
3 pa za k1 = 1,
k2 = 3 dobivamo samo popločavanje ravnine
kvadratima prikazano na slici 2.
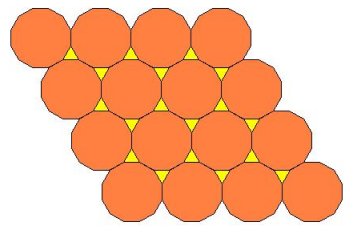
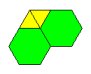
U ovom slučaju dobivamo dvije mogućnosti za n1 i n2 koje zadovoljavaju sve uvjete:
 |
 |
 |
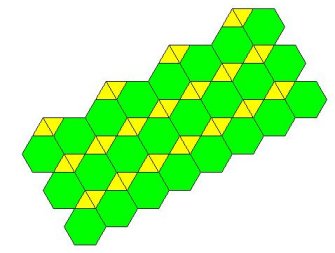 |
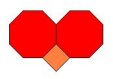
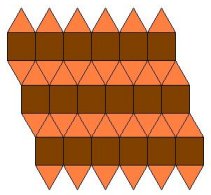
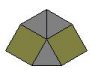
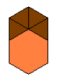
Jedino rješenje koje dobivamo u ovom slučaju je popločavanje dvama kvadratima i četirima jednakostraničnim trokutima. No, tu opet imamo dvije mogućnosti: (3,3,3,4,4) i (3,3,4,3,4). Odgovarajuća popločavanja prikazana su na slikama 9 i 10. Oba zadovoljavaju sve uvjete Arhimedovog popločavanja ravnine.
 |
 |
 |
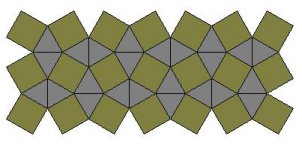 |
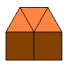
U ovom slučaju jedino rješenje je n1 = 6, n2 = 3. Radi se o Arhimedovom popločavanju ravnine četirima jednakostraničnim trokutima i jednim pravilnim šesterokutom (slika 11). Označavamo ga (3,3,3,3,6).
 |
 |
Ovim smo riješili slučaj popločavanja ravnine dvjema različitim vrstama pravilnih mnogokuta. Ostaje još slučaj popločavanja ravnine trima različitim vrstama pravilnih mnogokuta. Neka se u jednom čvorištu sastaje k1 pravilnih n1-terokuta, k2 pravilnih n2-terokuta i k3 pravilnih n3-terokuta. Iz uvjeta da zbroj veličina kutova oko jednog čvorišta iznosi 360° dobivamo diofantsku jednadžbu
| k1 |  |
(n1-2) 180° 180°n1 |
+ | k2 |  |
(n2-2) 180° 180°n2 |
+ | k3 |  |
(n3-2) 180° 180°n3 |
= 360°, | (8) |
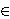
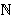 , n1, n2,
n3
, n1, n2,
n3 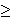 3.
Analognim zaključivanjem kao ranije dobijemo uvjet na k-ove koji glasi
3.
Analognim zaključivanjem kao ranije dobijemo uvjet na k-ove koji glasi
k1 (1/2 - 1/n1) + k2 (1/2 - 1/n1) + k2 (1/2 - 1/n2)
+ k3 (1/2 - 1/n2)
+ k3 (1/2 - 1/n3)
= 1. (1/2 - 1/n3)
= 1. | (9) |
Imamo tri bitno različita rješenja ove diofantske jednadžbe:
Uvrštavanjem odgovarajućih k-ova u jednadžbu (9) dobivamo diofantske jednadžbe, koje rješavamo analogno prethodnim slučajevima. U prvom slučaju dobivamo popločavanje ravnine kvadratom, pravilnim šesterokutom i pravilnim dvanaesterokutom, u oznaci (4,6,12). Prikaz ovog popločavanja dan je na slici 12.
 |
 |
Rješenje drugog slučaja je popločavanje ravnine jednakostraničnim trokutom, dvama kvadratima i pravilnim šesterokutom u poretku (3,4,6,4) (slika 13).
 |
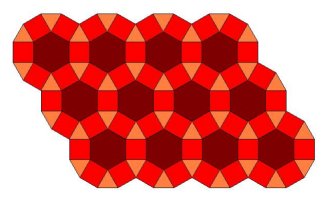 |
Ostaje nam riješiti još slučaj k1 = 3,
k2 = k3 = 1. Tražimo razdiobe ravnine
na tri različite vrste pravilnih mnogokuta. Pretpostavimo da imamo razdiobu na tri
jednakostranična trokuta, jedan kvadrat i jedan pravilni peterokut. Tada zbroj veličina
kutova oko jednog čvorišta iznosi 3 60° + 90° + 108° = 378°, što je veće od 360°.
Jednakostraničan trokut, kvadrat i pravilni peterokut su pravilni mnogokuti s
najmanjom veličinom unutrašnjih kutova. Ako zamijenimo bilo koji od tih triju mnogokuta
nekim drugim, tada će zbroj veličina kutova oko čvorišta biti još veći. Zaključujemo
da ovaj slučaj nema rješenja.
60° + 90° + 108° = 378°, što je veće od 360°.
Jednakostraničan trokut, kvadrat i pravilni peterokut su pravilni mnogokuti s
najmanjom veličinom unutrašnjih kutova. Ako zamijenimo bilo koji od tih triju mnogokuta
nekim drugim, tada će zbroj veličina kutova oko čvorišta biti još veći. Zaključujemo
da ovaj slučaj nema rješenja.
Sada smo iscrpili sve mogućnosti. Dobili smo ukupno osam Arhimedovih popločavanja ravnine i tako dokazali sljedeći teorem.
| Teorem 3. Postoji ukupno osam Arhimedovih popločavanja ravnine. |
Na kraju još jednom navodimo slike Arhimedovih popločavanja.
 (3,12,12) |
 (4,8,8) |
 (3,3,4,3,4) |
 (4,6,12) |
 (3,6,3,6) |
 (3,4,6,4) |
 (3,3,3,4,4) |
 (3,3,3,3,6) |
U ovom članku proučavali smo pravilna i Arhimedova popločavanja ravnine pravilnim mnogokutima. Problem popločavanja ravnine lijep je primjer primjene Descartesove metode, tj. svođenja realnog problema na matematički, točnije geometrijski problem, a njega na algebarski, odnosno na rješavanje diofantske jednadžbe. O primjeni problema popločavanja u nastavi matematike u osnovnoj i srednjoj školi može se pročitati u diplomskom radu [KR]. Tamo je također dan detaljniji dokaz teorema 3, u kojem su do kraja raspisani svi slučaji.
Slike u ovom radu programirane su u programskom jeziku Logo, koji također ima metodičku vrijednost i lijepa je poveznica matematike s nastavom informatike. Programi koji crtaju slike dostupni su ovdje. Izrađeni su uz pomoć Logo interpretera Terrapin Logo, ali rade i na drugim Logo interpreterima. Jedan besplatan interpreter na kojem ih se može koristiti je Comenius Logo.
[BI] S. Bilinski, Problem parketiranja. Matematičko-fizički list 196 (1999), 194-198.
[GK] V. Galešev, I. Kniewald, L. Kralj, G. Sokol, Informatika 6 - multimedijski priručnik informatike za 6. razred osnovne škole. SysPrint, Zagreb, 2004.
[K1] I. Kniewald, Logo 4.0. Alfej, Zagreb, 1999.
[K2] I. Kniewald, Terrapin Logo. SysPrint, Zagreb, 2005.
[KO] A.N. Kolmogorov, Parketi iz pravilnih mnogokuta. Matematika i škola 10 (2001), 216-218.
[KR] K. Krulić, Popločavanja ravnine i njihova primjena u nastavi matematike u osnovnoj i srednjoj školi. Diplomski rad, Sveučilište u Zagrebu, 2005.
[TO] L.F. Toth, Reguläre Figuren. Akademiai Kiado, Budapest, 1965.
[SR] S. Sruk, Simetrično je lijepo. Matematika i škola 10 (2001), 213-216.
[W1] E.W. Weisstein, Regular Tessellation. http://mathworld.wolfram.com/RegularTessellation.html
[W2] E.W. Weisstein, Tessellation. http://mathworld.wolfram.com/Tessellation.html
1. Problem popločavanja ravnine
2. Pravilna popločavanja ravnine
3. Arhimedova popločavanja ravnine
4. Zaključak
Literatura