Hrvatski matematički elektronski časopis math.e

http://web.math.hr/mathe/

8. MEDITERANSKO MATEMATIČKO NATJECANJE

Zagreb, 16. travnja 2005.

Zadaci


  1. Profesor je rekao Petru produkt dvaju prirodnih brojeva, a Slavku zbroj tih dvaju brojeva. Nijedan od njih na početku nije znao broj koji je bio poznat drugom dječaku.

    Jedan od dječaka rekao je drugome: Nema načina da odrediš moj broj.
    Na to drugi dječak odgovori: Varaš se, tvoj broj je 136.

    Koji je broj rekao profesor svakom dječaku? Obrazložite odgovor!

  2. Neka su k i k' dvije koncentrične kružnice sa središtem u točki O, te odgovarajućim polumjerima R i R' (R < R'). Zraka Ox siječe k u točki A. Nasuprotna zraka Ox' siječe k' u točki B. Treća zraka Ot (različita od prethodne dvije) siječe k u E i k' u F.

    Dokažite da kružnice (OAE), (OBF), kružnica s promjerom EF i kružnica s promjerom AB prolaze istom točkom.

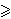  3. Neka su A1, ... , An (n >= 3) konačni skupovi prirodnih brojeva. Dokažite da vrijedi:

    1/n sum |A_i| + 1/n (n 3) sum |A_i cap A_j cap A_k| <= 2/(n 2) sum |A_i cap A_j|

    pri čemu je |E| oznaka za broj elemenata skupa E.

  4. Neka je A skup polinoma stupnja 3 s vodećim koeficijentom 1 koji imaju sljedeće svojstvo: za svaki polinom f(x) iz A postoje prost broj p koji ne dijeli 2004 i prirodan broj q koji je relativno prost s p i s 2004, takvi da je f(p) = 2004 i f(q) = 0.

    Dokažite da postoji beskonačni podskup B podskup A takav da su grafovi svih polinoma iz B identični do na translaciju.